这是Eliezer Yudkovsky的一篇文章的翻译，该文章来自致力于量子力学多元解释的流行科学周期。 周期的开始被翻译为中心 ，但是译者显然很累。 可以理解-该材料非常庞大。 尤德科夫斯基（Yudkovsky）喜欢在树上传播思想。 另一方面，材料确实很复杂，用不同的语言重复同一件事，至少会使不准备阅读的人头脑中的图片停留在某种程度上。 我不会保证继续翻译整个周期，但会尝试翻译一些最重要的文章。

我将跳过该系列中有关状态空间（ 经典空间和量子空间）的文章-这个概念在很多地方都使用过，并且对技术训练有素的读者应该很熟悉。 并且也跳过费曼路径积分 -它们可以在优秀的科普资料中找到 。

但是下一篇文章回答了一个重要问题。 如果从根本上说“真实”世界是量子的，那么一切都被混淆了并且一切都相互影响，那么古典系统从何而来？ 为什么我们在普通生活中很少见到“自然”量子现象？ 这就是作者所说的“经典幻觉”。 例如，为什么量子计算机的创造者需要付出巨大的努力才能使系统保持“自然”纠缠状态？

免责声明：我既不是专业物理学家，也不是专业翻译家（也是原著的作者）。

退相干

要了解称为退相干的量子过程，您首先需要了解如何破坏特殊的量子独立状态 -即，量子系统如何准确地从独立状态转变为纠缠状态。

我们记得 ，量子独立性是振幅分布的一种特殊的“矩形”状态，可以很好地分解。 也就是说，它可以表示为系统组成部分的分布的乘积，对我们来说，这看起来像是“分离的粒子”。

胆小的游客访问我们的量子世界时，有时会缺乏这种“矩形”分布，因为它们之间存在一些特殊的神秘联系。 因此，不幸的术语是“量子纠缠”。 实际上，量子系统的任何演化通常都会因独立性而产生纠缠（反之则不然），从而将矩形分布变成非矩形分布。 独立是罕见的，而且很容易破坏。

为了更好地了解究竟是什么物理过程导致纠缠，我们从经典系统开始。 该图显示了一个在上部轨道上带正电的轻球和在下部轨道上带负电的重球的系统。 最初，两个球相距很远并且几乎不相互作用。 然后，我们降低上部路径，将球聚集在一起，使它们开始相互吸引（相反的电荷被吸引）。 一个轻球滚成一个重的球（一个重球滚成一个轻的球，就像一个下降的苹果将地球轻轻地吸引到自己）。

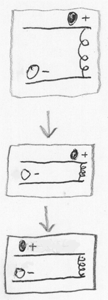
现在，从费曼路径积分的角度来看，让我们将此系统视为一个量子系统。 也就是说，我们将系统的演化表示为来自配置空间中初始状态的所有可能轨迹的总和。 假设两个球最初是量子无关的，则它们的振幅联合分布可以表示为“下部球的分布”和“上部球的分布”的乘积。

此外，让下部球在开始时的振幅包括三个部分（从费曼积分的角度来看，可以将其视为三个初始状态）。 当我们降低上部轨道时，应该将上部球拉到下部轨道。 但是，如果下部球的关节幅度由几个部分组成，那么最后，我们将获得由几个部分组成的关节分布，每个部分都描述了球的新位置。

我尽力避免使用诸如“较低的球可以在三个位置之一”或“在每种可能的情况下，较高的球都吸引到较低的球的相应位置”这样的表述。 虽然您可能仍然会以这种方式想象所有事情。 最后，我自己已经说明了这一点。 我画了三个可能的起始位置和三个可能的结果。 该怎么办，人脑通常想象费曼积分。 但这并不意味着宇宙存在三种可能的状态 。 这只是可视化路径积分的一个技巧。 振幅的所有三个分量都存在于我们的宇宙中，所有三个分量都是同等真实的 ，但是根本不可能或不可能 。

现在想象一下，首先，下球的振幅在整个轨迹上被“抹去”。 上球的振幅仍集中在一处。 然后，关节分布最初将是细长矩形的形式，然后变成对角线。

在X轴上是上部球的位置，在Y轴上是底部。 我们从一个精确定位的上球和一个“模糊的”下球开始，当两个坐标都模糊但彼此相等（简化）时，以相互依赖的分布结束。 也就是说，最初可分解的分布变成了一个“混乱的系统”-它不再分解成两个独立的因子。

（重要提示：

请注意，在上图中，系统的发展遵循热力学第二定律 ，即Liouville定理。 当系统更改时，将保留“云大小”，即振幅的总体积，或更简单地，保留图形上灰色区域的大小 。 如果在图的开始处有一个巨大的浅灰色正方形（当两个粒子都强烈涂抹在空间中时），那么根据热力学第二定律，它就不能变成深灰色对角线。 为了进入纠缠状态，系统最初应具有较低的熵，并且在此过程中该熵不应增加太多。

让我提醒您，互信息是带有相反符号的熵 。 量子振幅并不完全是信息 ，但原理是相同的。 初始振幅应足够集中以产生紧凑的对角线，而不是大的稀疏云。 如果我们假设振幅分布具有“量子熵”，那么纠缠系统的熵应该相对较低）

最后，我们准备谈论不连贯。

图中的系统非常复杂。 可以这样描述：“有两个粒子，而且它们都可以在这里或那里 。” 是的，我将其表述为好像存在两种可能的状态，而不是振幅的物理真实分布。 认真地说，我不知道如何用普通语言描述量子物理学！ 只要记住一般规则 ，即“机会”或“概率”是“物理存在的幅度分布范围”的缩写。 然后，我可以使用不确定性来描述幅度更短的幅度。 但是请记住，这只是一个约定 ！ “粒子在这里或那里”是指“物理上存在的两个部分的振幅分布，一个在这里，一个在那”，而不是 “粒子在两个位置之一，但我们不知道哪个”。

这样啊 通常很难使用复杂的系统（对于物理学家而言，对宇宙而言并非如此）。 首先，我们必须为所有可能的初始条件计算所有可能的轨迹（即，考虑到Feynman积分中所有物理上存在的振幅轨迹）。 此外，有必要考虑这些轨迹之间的相互影响（ 严格意义上的可能轨迹不能相互作用-只有真正存在的某些事物才能影响其他事物）。 例如，我们的两个粒子与另外20个粒子相遇，并以某种方式相互作用，结果，我们得到了一堆受所有可能状态的所有先前点影响的配置。

注意，仅当初始振幅的各个部分彼此靠近时才发生纠缠。 这样他们的发展道路可以相交。 如果两个粒子位于此处或那里 ，但“此处”和“那里”之间的距离为两个光年，则它们的进一步轨迹可以不早于一年后相交。

现在添加第三个粒子。 该图显示了一个三维配置空间，该空间分解为独立的二维和一维子空间。 也就是说，两个纠缠的粒子相互独立。

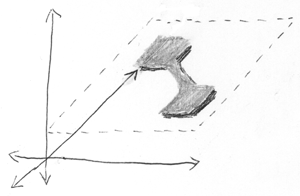
高度是第三个粒子，宽度和深度是两个纠缠的粒子。

一个独立的粒子在某个位置-垂直分布非常狭窄。 两个纠缠的粒子在这里或那里 （我再次使用了不正确的概率术语，例如“特定”和“任一个”，但您理解我的意思）。

现在想象一下，第三个粒子与纠缠的两个粒子反应时，对它们的位置很敏感。 例如，第三个粒子在一个尖峰上平衡，两个粒子飞过，吸引了它，然后以一种或另一种方式掉落。 之后，振幅看起来像这样。

现在，第三个粒子与其他两个混淆。 现在振幅由彼此分开的两部分组成。 简化描述：“如果这里有两个粒子，那么第三个粒子会飞到这里 。 如果他们在那 ，那么她就飞到那了 。“ 即，振幅已经变得完全混乱。 它不再分解成独立的子空间。

但是，现在两个振幅分开了 ，每个振幅都由对应区域中的三个粒子组成。 发生这种情况是因为第三个粒子对其他粒子的坐标敏感。 从尖峰滚动到两侧之一后，最终坐标之间的距离非常大。

实际上，从顶部向下滚动是可选的。 如果您有二十个粒子对前两个粒子做出反应并与它们混淆，则一切工作原理都相同。 22维空间中的最终分布将看起来像两个区域，每个区域对应于22个粒子。 这些区域之间的距离将是巨大的。 并且距离越远，将来的区域相互影响的可能性就越小。
这就是退相干。 这是“经典幻觉”的第三个原因，因为这两个领域开始独立发展。 这使得它们可以描述为非复杂系统。 一旦我们分别考虑它们，它们中每个的分布看起来都是“矩形”，并且在三个坐标中是独立的（我试图在上图中显示）。

在量子计算机中，很难防止退相干。 量子计算要求振幅部分保持彼此靠近并且可以相互作用。 但是周围还有数万亿个其他粒子，它们一直在不经意间与我们脆弱的量子比特发生反应，破坏了精确构建的振幅。

而且，您不能只是拿走并恢复被摧毁的东西。 为此，必须将所有反应的粒子（ 包括来自环境的随机粒子）返回到该位置（不要忘记，最终振幅与它们具有联合分布）。

（这似乎是一个几乎不可逆的过程，对吗？这就像是试图将破碎的鸡蛋收集回壳中。实际上，这是一个很好的类比。

这就是为什么我之前强调了纠缠过程以低熵开始的原因。 退相干是不可逆的，因为它本质上是一个热力学过程。

基本的物理原理之一是，您可以在不违反基本定律的情况下“还原胶片”。 如果您拍下一个掉落在地板上的鸡蛋然后向后滚动，使破损的鸡蛋从地板上飞起来，聚集回到光滑的外壳中，您将不会看到任何违反物理规律的情况。 所有分子都将在正确的时间被正确地放置在正确的位置，并且鸡蛋会安全，健康地从地板上弹起。 这并非不可能，只是极不可能。

破碎成遥远部分的振幅也是如此，意外地返回到相干状态-理论上这是可能的。 但是实际上几乎没有机会将最初断开的片段突然同时相邻放置。 逆向过程的可能性更大。

实际上，除了向后滚动影片外，还需要反转所有粒子的电荷，并左右互换（或其他两个维度之一），从而将宇宙变成其镜像。 该规则在费用，奇偶校验和时间一词中称为“ CPT不变性”。

CPT不变性很可能是宇宙运行的最基本原理之一。 对于物理学家来说，打破它的尝试几乎和试图以比光速快的速度扔球一样荒谬。 据我所知，CPT不变性是量子场论一致性的必要条件。

因此，退相干看起来仅是一个单向过程，但实际上其不可逆性是热力学的，不是根本的。 这一点非常重要，因为量子物理学由此观察到CPT不变性。

据我们所知，自然界中绝对所有的单向过程都是热力学第二定律的结果，而不是时间的基本不对称性。）

总结一下。 退相干是不断增加的量子纠缠的热力学过程，令人惊讶地伪装成破坏该纠缠本身的过程。 不相干的区域不会相互影响，并且每个区域都变得不那么混乱 。 退相干是“经典幻觉”的第三个原因。 它使物理学家可以将每个场都视为独立的场，而无需考虑它们相互作用的微不足道的可能性。 此外，每个单独的区域在中变得更容易理解。 如果要解决简单经典物理学方面的问题，这将非常有用。 如果您想在太阳出来之前将一百万位数字分解为数字，这是非常不适当的。