朋友你好 “
开发人员算法”课程将于明天开始，而我们还有一份未出版的翻译。 实际上，我们会更正并与您共享材料。 走吧
快速傅立叶变换（FFT）是最重要的信号处理和数据分析算法之一。 我使用它多年没有计算机科学方面的正式知识。 但是这周对我来说，我从来没有想过FFT如何如此迅速地计算出离散傅立叶变换。 我从一本关于算法的旧书上除掉了灰尘，打开了书，并愉快地阅读了J.V. Cooley和John Tukey在
1965年有关该主题的经典著作中描述的看似简单的计算技巧。
这篇文章的目的是深入研究Cooley-Tukey FFT算法，解释导致它的对称性，并展示一些在实践中应用理论的简单Python实现。 我希望这项研究可以使数据分析专家（例如我自己）对我们使用的算法背后正在发生的事情有更全面的了解。
离散傅立叶变换FFT快速
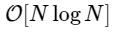
一种用于计算离散傅里叶变换（DFT）的算法，该算法直接为
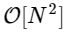
。 像更熟悉的傅立叶变换的连续版本一样，DFT具有正反形式，其定义如下：
直接离散傅立叶变换（DFT）：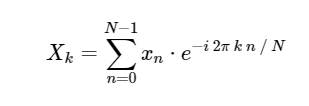
离散傅立叶逆变换（ODPF）：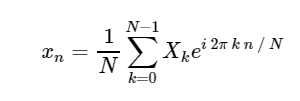
从
xn → Xk的转换是从配置空间到频率空间的转换，对于研究信号功率谱和转换某些任务以进行更有效的计算都非常有用。 您可以在
我们未来的天文学和统计学
书的第10章中找到一些实际的例子，在这里您还可以找到图像和Python源代码。 有关使用FFT简化否则复杂的微分方程式积分的示例，请参阅我的文章
“在Python中求解Schrödinger方程式” 。
由于FFT的重要性（在下文中，可以使用等效的FFT-快速傅立叶变换）在Python的许多领域中都包含许多用于计算它的标准工具和外壳程序。 NumPy和SciPy都具有经过严格测试的FFTPACK库的外壳程序，它们分别位于
numpy.fft和
scipy.fftpack 。 我知道最快的FFT在
FFTW包中，在Python中也可以通过
PyFFTW包获得。
然而，目前，让我们将这些实现放在一边，想知道如何从头开始用Python计算FFT。
离散傅立叶变换计算为简单起见，我们将只处理直接转换，因为可以以非常相似的方式实现逆变换。 查看DFT的上述表达式，我们看到的不过是简单的线性运算：将矩阵乘以向量
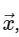
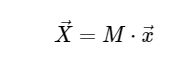
给定矩阵M
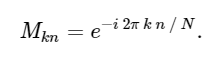
考虑到这一点，我们可以使用简单的矩阵乘法计算DFT，如下所示：
在[1]中：
import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)
我们可以通过将结果与numpy内置的FFT函数进行比较来再次检查结果：
在[2]中：
x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))
0ut [2]：
True只是为了确认我们算法的慢度，我们可以比较这两种方法的执行时间：
在[3]中：
%timeit DFT_slow(x) %timeit np.fft.fft(x)
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
我们的速度要慢1000倍以上，这对于这种简化的实现是可以预期的。 但这不是最坏的情况。 对于长度为N的输入向量，FFT算法的缩放比例为
而我们的慢速算法会像
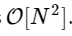
。 这意味着
元素，我们希望FFT在约50毫秒内完成，而我们的慢速算法将花费约20个小时！
那么FFT如何实现这种加速呢？ 答案是使用对称性。
离散傅立叶变换中的对称性建立算法中最重要的工具之一是任务对称性的使用。 如果您可以分析表明问题的一部分与另一部分简单相关，则可以只计算一次子结果并节省此计算成本。 Cooley和Tukey正是使用这种方法来获取FFT。
我们从意义问题开始
。 根据上面的表达式：
其中，我们使用恒等式exp [2πin] = 1，它适用于任何整数n。
最后一行很好地显示了DFT的对称性：
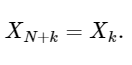
一个简单的扩展
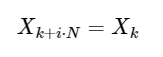
对于任何整数i。 如下所示，这种对称性可以用来更快地计算DFT。
FFT中的DFT：使用对称性Cooley和Tukey表明FFT计算可以分为两个较小的部分。 根据DFT的定义，我们有：
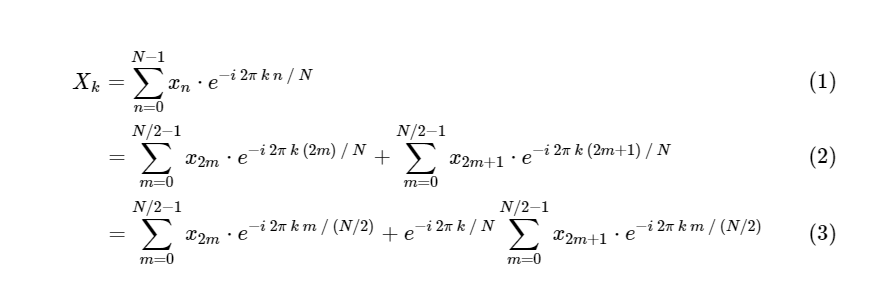
我们将一个离散傅立叶变换分为两部分，它们本身与较小的离散傅立叶变换非常相似，一个是奇数值，一个是偶数值。 但是，到目前为止，我们还没有保存任何计算周期。 每个项包括（N / 2）* N个计算，总计
。
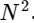
诀窍是在每种情况下都使用对称性。 由于k的范围是0≤k<N，n的范围是0≤n<M≡N/ 2，我们从上面的对称性中看到，对于每个子任务，我们只需要执行一半的计算。 我们的计算
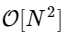
已经成为
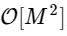
其中M小于N的两倍。
但是没有理由对此进行详细说明：只要我们较小的傅立叶变换的偶数为M，我们就可以重新应用这种分而治之的方法，每次将计算成本减半，直到我们的数组足够小以至于该策略不再受益。 在渐近极限中，此递归方法的缩放比例为O [NlogN]。
当子任务的大小变得很小时，可以从我们的慢速DFT代码开始，在Python中非常快地实现此递归算法：
在[4]中：
def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32:
在这里，我们将快速检查我们的算法是否给出正确的结果：
在[5]中：
x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))
出[5]：
True将此算法与我们的慢版本进行比较：
-在[6]中：
%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
我们的计算比直接版本更快！ 而且，我们的递归算法是渐近的
：我们实现了快速傅立叶变换。
请注意，我们仍然不接近numpy内置FFT算法的速度，这是可以预期的。
fft numpy背后的FFTPACK算法是一种经过多年改进和优化的Fortran实现。 另外，我们的NumPy解决方案包括Python堆栈的递归和许多临时数组的分配，这增加了计算时间。
使用Python / NumPy时，加快代码速度的一个好策略是在可能的情况下向量化重复计算。 我们可以这样做-在此过程中，删除递归函数调用，这将使我们的Python FFT更加高效。
矢量化的Numpy版本请注意，在上述FFT递归实现中，在最低递归级别上，我们执行
N / 32个相同的矩阵矢量乘积。 如果同时将这些矩阵向量乘积计算为一个矩阵矩阵乘积，则算法的有效性将获胜。 在每个后续递归级别，我们还执行可以向量化的重复操作。 NumPy在这种操作方面做得非常出色，我们可以利用这一事实来创建此快速傅里叶变换的矢量化版本：
在[7]中：
def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2")
尽管该算法更加不透明，但它只是对递归版本中使用的操作的重新排列，但有一个例外：我们在计算系数时使用对称性，仅构建了一半的数组。 同样，我们确认我们的函数给出了正确的结果：
在[8]中：
x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))
出[8]：
True随着我们的算法变得更加高效，我们可以使用更大的数组比较时间，而剩下
DFT_slow ：
在[9]中：
x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
我们已将实施方式提高了一个数量级！ 现在，仅使用几十行纯Python + NumPy，我们离FFTPACK基准测试大约10倍。 尽管这在计算上仍然不一致，但是就可读性而言，Python版本远远优于FFTPACK源代码，您可以
在此处查看。
那么FFTPACK如何实现最后的加速呢？ 好吧，基本上，这只是详细的簿记问题。 FFTPACK花费大量时间重用任何可重用的中间计算。 我们衣衫version的版本仍然包括过多的内存分配和复制； 在诸如Fortran之类的低级语言中，可以更轻松地控制和最小化内存使用。 另外，Cooley-Tukey算法可以扩展为使用大小不是2的分区（我们在这里实现的就是以2为基础的Cooley-Tukey Radix FFT）。 也可以使用其他更复杂的FFT算法，包括基于卷积数据的根本不同的方法（例如，参见Blueshtein算法和Raider算法）。 上述扩展和方法的结合即使在大小不是2的幂的阵列上也可以实现非常快速的FFT。
尽管纯Python中的函数在实践中可能没有用，但我希望它们能对基于FFT的数据分析背景中发生的事情提供一些见识。 作为数据专家，我们可以应对由具有更高算法意识的同事创建的基础工具“黑匣子”的实现，但是我坚信，对于对应用于数据的低级算法的了解越多，实践就越好。我们会的。
这篇文章完全是用IPython Notepad写的。 完整的笔记本可在
此处下载或
在此处静态
查看 。
许多人可能会注意到该材料远非新鲜，但是，在我们看来，这是非常相关的。 通常，写出文章是否有用。 等待您的评论。