几位基于30年前鲜为人知的数学理论的数学家证明,类似肥皂膜的最小表面在各种各样的图形上大量出现

2011年底,
布莱恩·怀特 (
Brian White)偶尔听到斯坦福办公室门口的敲门声。 在外面,此时此刻,两位年轻的数学家正在等着他,分别是
费尔南多·科达·马克斯 (
Fernando Coda Marquez)和
安德烈·尼维斯 (
Andre Nevis) ,他们总是有同样的问题:怀特有几分钟的时间来帮助他们弄清楚几百篇鲜为人知的论文的晦涩部分三十年前写的页面?
由
约翰·皮特斯 (
John Pitts)撰写的论文提出了一种强大的机制,可以在各种形状中构造最小的表面(类似于肥皂膜和气泡的结构)。 当可以在图形上构建最小表面时,图形可以研究图形周围空间的几何形状。 从黑洞的研究到生物分子的发展,这样的表面出现在各种科学问题中。
然而,这些年来,皮茨的论文一直不在学者的关注范围之内-也许是因为它难以阅读。 马尔克斯和尼维斯深信其中蕴藏着巨大的潜力。 内维斯说:“对我们来说,很明显,这一理论被完全低估了,而没有引起人们的注意。”
尼维斯说,尽管怀特从来没有问过这对夫妇为什么对皮茨的工作感兴趣,但他们每次都说他们的兴趣“纯粹是学术性的”。 但是,他们有一个明确的目标-证明50年前的威尔莫尔假说,该假说解决了寻找可能的最佳甜甜圈形状的问题(稍后会详细介绍)。 经过3个月的努力,皮克斯(Pitts)的论文才得以
实现 ,马尔克斯(Marquez)和尼维斯(Nevis)
实现了他们的目标 ,获得了许多奖项和正面评价。
但是在过去的几年中,他们已经能够将Pitts的想法推得更远。 皮茨和策展人弗雷德里克·阿尔姆格伦(Frederick Almgren)找到了一种方法,可以确保少量尺寸的每个人物都至少具有一个最小曲面。 现在,马克斯(Marquez)和尼维斯(Nevis)根据阿尔姆格伦(Almgren)和皮特(Pitts)的思想,利用聚集在他们周围的年轻数学家的队伍,表明在一般情况下,这些形式应该包含许多最小的表面-无限多个表面拥挤并拥挤在人物的各个角落。 “这是一个巨大的突破,”德克萨斯大学著名的几何学家
Karen Uhlenbeck在一封电子邮件中给我们写信。
加州大学欧文分校的
理查德·肖因说:“要创建一个最小的表面需要花费很多精力。”约15年前曾为尼维斯提供建议。 “它们太多了,真是太神奇了。”
过去几年,对阿尔姆格伦和皮茨理论的复兴,导致了活动的爆炸式增长。 怀特说:“结果是如此之快,而且数量如此之多,以至于很难追踪它们。” “对我来说,这看起来非常有趣和美妙。”
标记山脉
将弯曲的线浸入肥皂溶液中,或吹肥皂泡,液体将迅速形成尽可能小的区域的表面。 这些最小曲面的几何形状已经占据了数学家数百年的历史。 它们出现在各个领域,从建筑的最小表面激发屋顶和其他结构的设计,到产生用于药物输送的微粒。 五年前,当一组科学家
创造出能够在内部携带药物或荷尔蒙的
多孔分子时 ,他们发现某些分子采取了
螺旋状的形式,即无尽重复的表面,其部分类似于肥皂膜。
从技术上讲,数学家仅将电线上的肥皂膜视为具有最小表面的表面,而不考虑肥皂泡,因为在没有空气分子的抽象空间中,气泡会缩小到一个点。 但是,导线上的薄膜不能完全满足数学家的要求。 它的内部是光滑的表面,但是其导线会急剧折断。 考虑是否有可能将该表面扩展到导线边界的边界之外,这样在每个单独的区域中看起来都像肥皂膜一样,这是合乎逻辑的。 有时这是可能的,并且表面延伸到无穷大。 有时,表面返回并与自身尴尬相交,或遇到其他困难。
 陀螺-一种设计用于药物输送的微粒时出现的最小表面
陀螺-一种设计用于药物输送的微粒时出现的最小表面在普通空间中,这将耗尽所有可能性。 但是数学家和其他科学家经常考虑不同于我们习惯的无限三维空间的其他世界-弯曲的或有限的,例如球体或圆环表面的三维类比。 这样的图形具有新的有趣的可能性:最小的表面会自身弯曲并锁定为不需要导线支撑的封闭最终图形。
在相对论中,这些有限的最小表面起着黑洞事件视界的作用。 而且,如果可以在任何图形上找到它们,这将有助于数学家从不同角度考虑其几何形状:他们提供了将图形(或
歧管 )切割成可能更简单的零件的模板,它们指示了歧管内正曲率的区域-分成几部分,向内弯曲,类似于球形或黑洞,而不是向外弯曲。
“我们对具有正曲率的歧管知之甚少,” Shoin说。
但是,通常很难证明图形中存在最小曲面。 要了解原因,请考虑此问题的二维版本。 寻找最小表面的问题在任何维度上都是有意义的:数学家简单地认为表面是一种形式,其尺寸比其所居住的空间小一个。 因此,在二维世界中,由连接附近点的最短路径组成的“大地测量”曲线将成为最小曲面。
对于某些二维图形,可以轻松地找到有限循环中闭合的测地曲线。 取一个圆环的表面-甚至不一定是均匀和对称的;让它有不规则和凸起。 如果将这样的甜甜圈包裹有一条穿过其中心的松紧带,我们可以想象如何将其拧紧并将其移动到各个可能的位置。 其中一条将是最短的-根据定义它将是一条测地线。
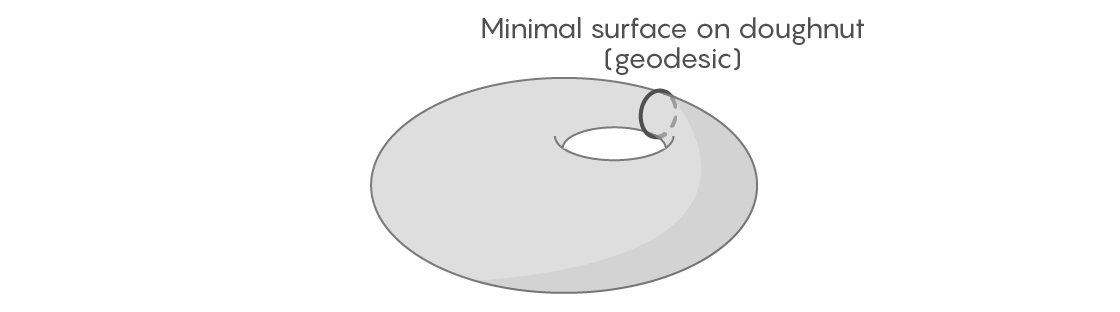
但是,如果这个领域是我们的形象,这种方法将不再起作用。 在完美平坦的球体上,很容易找到测地曲线-它将是赤道和其他完整的圆。 但是在一个不平坦的球体上,例如在地球表面上,尚不清楚测地曲线的位置以及是否有任何一个闭合的环。 您可以想象我们如何用松紧带包裹地球,例如甜甜圈。 但是,如果您开始移动它,并尝试将其缩短,它会缩小到一个点,因为与甜甜圈不同,该球体上没有孔可以紧贴弹性体。
但是,这种带有松紧带的惨败充满了成功的根源。 如果圆球的赤道被一条弹性带拦截,那么移动它的唯一方法-向其添加波浪-将使其变长。 如果以不同的方式将其上下移动到新的纬度,它将变短。 因此,从一个角度来看,赤道将是最短的曲线,而从另一个角度来看则将是最长的曲线。
这使得赤道与山pass的鞍峰有关,一侧的最高点(从穿过山脉的路径)而另一侧的最低点(从路径到附近的山峰)。 这不仅是一个较弱的类比:通常,最小的表面竟然是这样的鞍形物,但是它们的山脉却生活在一个很难想象的世界中。
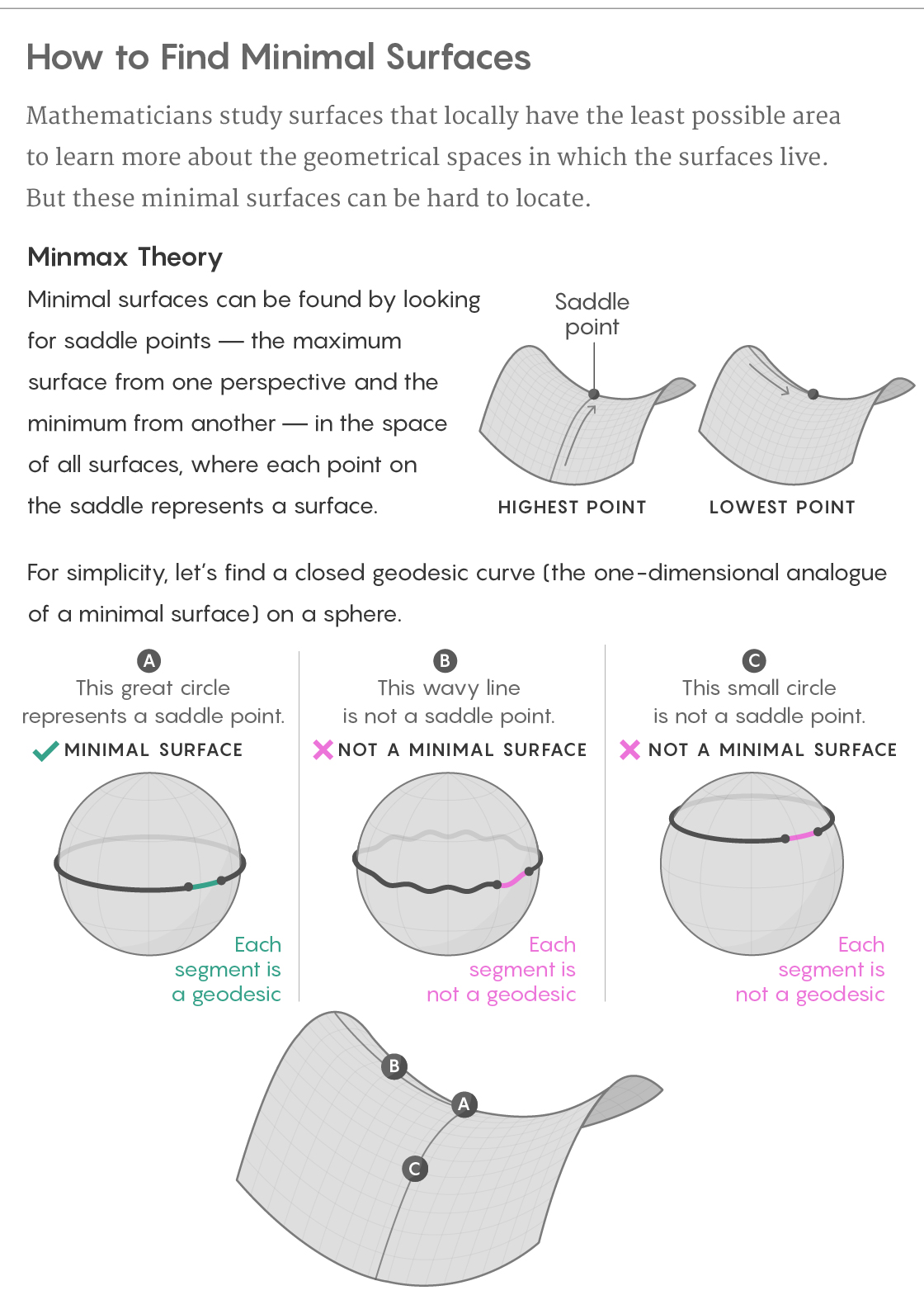
在确定图形的最小曲面时,我们可以考虑一个新世界,该世界由该图形中存在的所有可能的有限曲面组成-我们将其称为“曲面表面”。 曲面空间的每个点都完全对应于原始图形上的整个曲面。 然后,我们可以将每个表面的面积视为表面空间中相应点的高度,因此我们的世界将具有自然的地形。 在原始图形上搜索最小曲面将变为在曲面空间中搜索鞍形。
1917年,乔治·大卫·伯克霍夫(George David Birkhoff)
使用这种方法表明,任何颠簸或光滑的球都必须具有一条闭合的测地曲线。 大约六十年后,Almgren和Pitts通过在尺寸从3到7的所有有限图形上标记了曲面的表面形貌,从而巧妙地扩展了Birkhoff的思想,然后使用该形貌来证明这些图形始终至少具有一个封闭的最小曲面。 尼维斯说,皮特(Pitts)在1981年发表的关于Minmax理论的
论文“之所以如此,是因为鞍座既是最小值又是最大值”。
但是,这非常复杂。 Shoin说,很少有人能理解该理论的细微差别,一些研究该理论的数学家声称它尚未得到充分证实。 他说:“我认为毫无疑问,它非常有趣且重要。” “但是目前尚不清楚它有多饱满。”
Minmax理论方面的工作逐渐变得白热化。 尼维斯说:“数学界已经把皮茨的工作遗忘了大约30年。” 直到2006年尼维斯(Nevis)和马克斯(Marquez)在普林斯顿大学数学大楼的电梯中相遇后,她才复活。
越过山口
那时,马克斯(Marquez)到达普林斯顿(Princeton)进行演讲; 尼维斯在获得博士学位后不久就在那里找到了工作。 他们俩都以葡萄牙语为母语(Marquez来自巴西,Nevis来自葡萄牙),他们很容易找到一种共同语言。 “然后我第一次与他交谈,但他像我们已经成为朋友十年一样与我交谈,”现任普林斯顿大学教授的马克斯说。
然后他们发现讨论数学思想对他们来说同样自然。 他们有不同的风格:马克斯(Marquez)更镇定,尼维斯(Nevis)更热情。 但这对他们来说是一个加号。 “很难找到能很好地帮助您的人,”马克斯说。
两者都渴望找到可以浸入其中的一些复杂的数学问题。 几年来,尼维斯说,这对夫妇每走一次路,便会产生想法,以“看看延误了什么”。 “我们有上百万个创意,结果其中一个创意被过滤掉并变成了某种形式。”
过滤掉的问题原来是“威尔莫尔假说”的著名问题。 她建议找到一个圆环形状,这种形状将被称为Willmore能量的幅度最小化,大致来说,它测量给定形状与圆形球体之间的差异。 1965年,威尔莫尔(Wilmore)
提出 ,这将是最对称的形状的最圆的甜甜圈,称为
克利福德圆环 ,但是,尽管进行了许多尝试,但没有人能证明这一假设。
 马尔克斯(左)和尼维斯
马尔克斯(左)和尼维斯马尔克斯(Marquez)和尼维斯(Nevis)开发了一种有前途的方法,但是要使其起作用,他们需要最后一个要素:最小极大值理论。 他们认为掌握这一理论并编写最终作品将需要两到三周的时间-直到他们打开了皮茨的书。 “我们感到震惊-这是怎么回事? -尼维斯说。 “这本书非常干燥。”
分开的定理发展成许多页-但这仅仅是对定理的描述,而不是它们的证明。 主定理很难找到。 “我记得费尔南多是怎么来我办公室说的:我找到了定理的陈述!” -尼维斯说。
 托尔·克利福德
托尔·克利福德当他们陷入困境时,他们就向扑克牌求助,这是了解皮特斯大部分工作的少数人之一(尽管怀特本人将这些对话描述为“盲目,领导盲人”;得克萨斯州A&M大学教授皮茨本人毕业了)几十年前根据minmax理论撰写作品)。 尼维斯回忆说:“我们的积极性令人难以置信,因此我们能够取得突破。” “但这不是胆小的人的任务。”
当Marquez和Nevis完成对Wilmore假设的证明时,他们比其他任何数学家都更了解Minmax理论。 他们坚信,其潜力远远超出了假设的陈述范围。 尼维斯说:“我们知道我们有一个非常强大的理论。” -每次,使用该方法来证明长时间保持一定结果的特定结果时,您都会了解其中包含某些内容。 这表明值得继续深入研究。”
Almgren和Pitts的minmax图不仅产生一个鞍,而且产生无限数量的鞍。 从理论上讲,这应对应于无限数量的原始形状的最小曲面。 但是Almgren和Pitts无法证明以这种方式获得的最小表面是不同的。 因此,唯一可以肯定地说的是每个图形至少有一个最小的表面。
此后,“该主题的开发实际上已经停止了,”尼维斯说。 “这是30多年来最好的结果。”
需要一种新成分,马克斯和尼维斯找到了。 如2016年所示,无数的maxmax曲面的行为与鼓的频率相同。
1911年的数学家德国人魏尔(German Weil)表明,鼓的基本频率具有一种出乎意料的特性:概括地说,高频仅取决于鼓的体积,而不取决于其形状。 Marquez和Nevis以及麻省理工学院的
Eugene Lekumovich 表明 ,Minmax表面满足类似于鼓频率定律的数学定律。 特别是,表面积大致取决于它们所居住的空间量,而不是其形状。
这个结果终结了几十年前提出的假设,使Marquez和Nevis能够在2017年
展示 -这次是在东京大学的
Kay Air的帮助下-对于大多数数字而言,minmax列表包含无限数量的不同最小曲面。 而且,他们表明这些表面是“致密的”:它们出现在周围空间中每个点的旁边。 支持该结论的直觉是,为了让空间的体积确定最小表面的位置区域,后者必须以某种方式“看到”整个体积。 马尔克斯说:“这表明这些家伙千差万别。”
几个月后,这对夫妇与Marquez的研究生
Antoine Sun一起表明,如果仔细查看minmax曲面列表,您会发现它们
均匀地填充了空间 -数学家称之为“分配”。
怀特说:“当我听说它们分布均匀时,我感到很惊讶。” “看来我一生中人们不应该能够证明这样的结果。”
在最近几年中,又有几位数学家加入了这个问题。 例如,在一月份,加州大学圣塔芭芭拉分校的周欣基于Marquez和Nevis的先前工作
证明 ,对于大多数图形,Almgren和Pitts列表上的所有最小曲面彼此不同,这在这个问题上提出了一个很好的观点。 怀特说:“这确实很好地结束了这个主题,自80年代的阿尔姆格伦(Almgren)和皮特(Pitts)时代开始。”
这个结果系列考虑了几乎每个从3到7的数字,但最平滑的形式除外,无论多么违反直觉。 但是去年6月,Sunn能够
证明这些尺寸中的每个图形(包括最圆的图形)都具有无限多个闭合的最小曲面,这证实了几十年前的另一个假设。
尚不清楚密度和均分布是否会表现得一样均匀,以及minmax理论在紧凑型流形或八个或更多个维度上如何
不起作用 (但是,
新的工作在这里也取得了一些成功)。 数学家预测,我们将能够比看起来更快地回答许多问题。
尼维斯说:“一切发展都非常快。” “每周我都会浏览带有arxiv预印本的站点,并且在那里看到有人如何决定其他事情。”
从一个角度看,这些作品标志着一个故事的终结,或者说故事的终结,这个故事已经悬而未决了近四十年。 但这也是一个新的开始:数学家才刚刚开始理解,这些关于最小曲面的新思想可以告诉我们它们所居住的空间。
Shoin说:“我很可能会很快想到其他有趣的应用知识的方式,但是确切地说,我绝对不能说。”
“我相信这将是几何学的主要方向之一。”