哈Ha!
该出版物对我来说似乎很有趣:
我们从成对的交叉货币汇率中获得
绝对汇率,并且我想测试通过数值模型找到这种绝对汇率的能力,通常放弃线性代数。
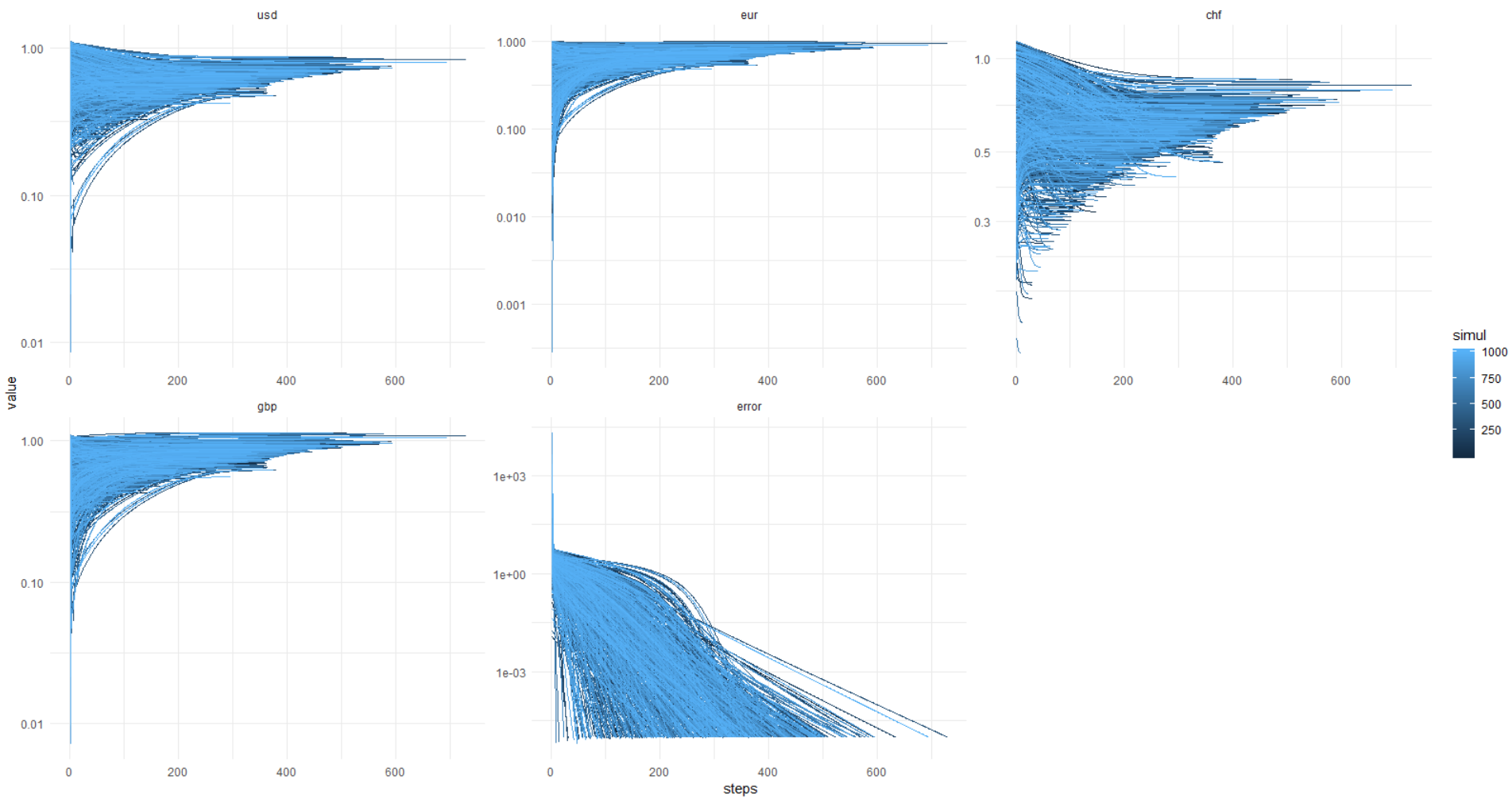
结果很有趣。
实验将很小:4个货币,6个货币对。 对于每一对,进行一次疗程测量。
所以我们开始吧
假设是,任何一种货币的价值都可以表示为一种值,该值将考虑其所引用的其他货币的价值,而其他货币本身将以所有其他货币的价值表示。 这是一个有趣的递归任务。
有4种货币:
对于他们,拨打了货币对:
- 欧元
- gbpusd
- eurchf
- urg
- gbpchf
- 美元汇率
请注意,如果货币数量为n = 4,则货币对数量为k =(n ^ 2-n)/ 2 =6。如果引用欧元,则寻找usdeur是没有意义的...
在时间t,测量其中一个提供者的汇率:
将针对这些值进行计算。
数学
我通过分析损失函数的梯度来解决问题,该函数本质上是一个方程系统。
实验代码将在R中:
R允许使用stats :: D接受函数的派生。 例如,如果我们想用美元货币区分,我们得到表达式:
2 *(欧元/美元^ 2 *(欧元-欧元/美元))+ 2 *(英镑/美元^ 2 *(英镑-
gbp / usd))-2 *(1 / CHF *(USDDCHF-USD / CHF))
为了减小express函数的值,我们将执行梯度下降,并且立即清楚(我们看到平方差)最小值将为零,这正是我们所需要的。
-deriv_vals * lr
梯度下降步骤将由参数lr控制,并且所有这些都带有负号。
也就是说,以人类的话来说,我们选择4种货币的汇率,以使实验中的所有货币对都获得等于这些货币对初始值的值。 嗯,让我们解决这个难题-在额头上!
结果
为了避免延展,我将立即通知您以下信息:整个实验都成功了,代码起作用了,错误接近了,接近于零。 但是后来我注意到结果总是不同的。
鉴赏家的一个问题:似乎这项任务有无数个解决方案,但在此我是一个完整的零,我想他们会在评论中告诉我。
为了验证解决方案的(非)稳定性,我模拟了1000次,而没有为货币值的起始值固定PRNG种子。
这就是kata的图片:误差总是达到0.00001或更低(以这种方式设置优化),而货币的价值则使魔鬼浮出水面,知道了哪里。 事实证明,总会有一个不同的决定,先生们!
再次显示此图片,y轴为原始单位(不是对数):
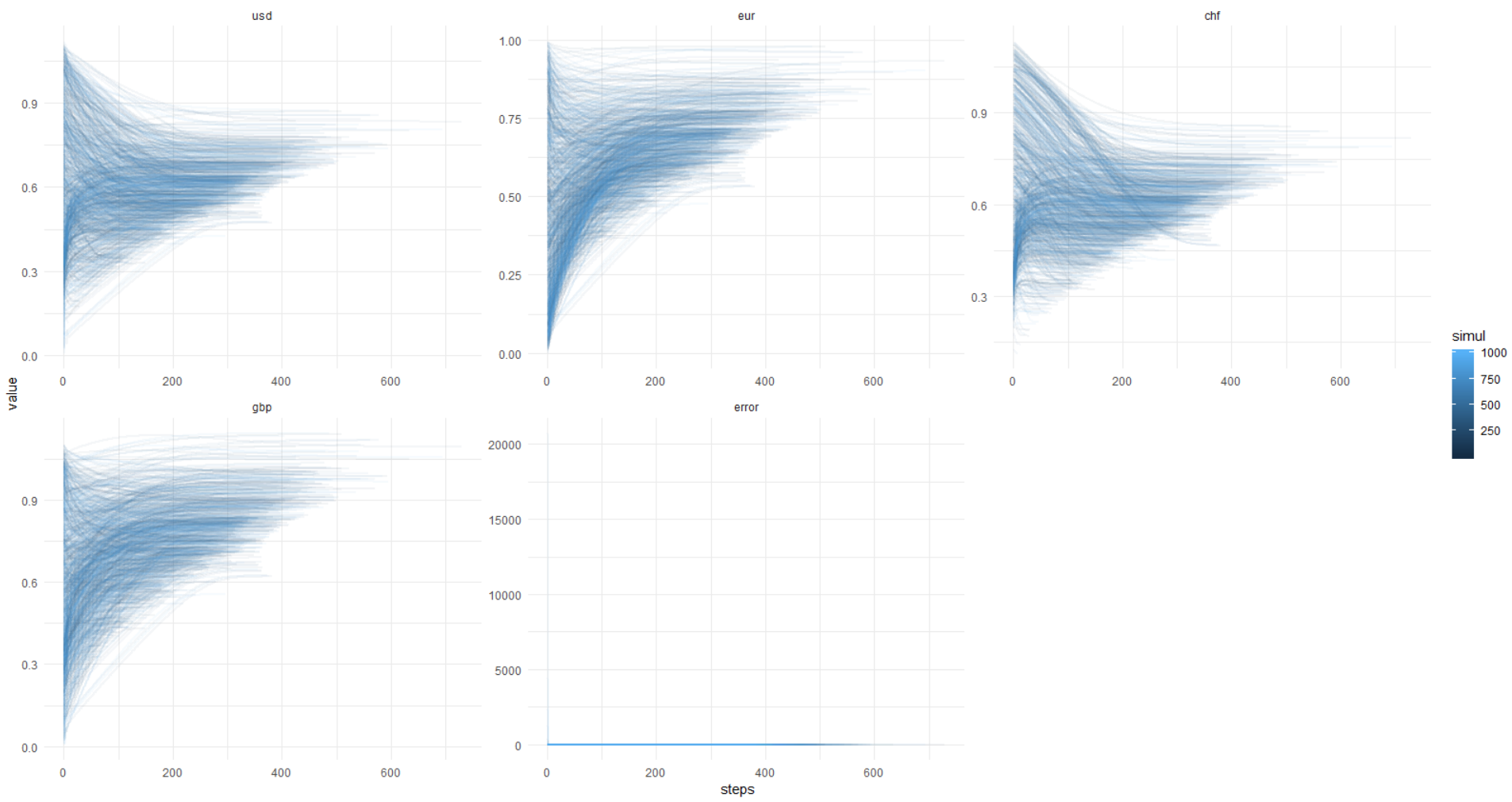
为了使您可以重复此操作,在下面附上完整的代码。
1000个模拟的代码可以工作大约一分钟。结论
这仍然是我不清楚的地方:
- 是否可以通过棘手的数学方法来稳定解决方案;
- 是否将有更多的货币和货币对汇合;
- 如果没有稳定性,那么对于每个新数据快照,如果您不修复PRNG种子,我们的货币将按照自己的意愿行事,这是失败的。
在没有任何可理解的前提条件和限制的情况下,整个想法似乎非常模糊。 但这很有趣!
好吧,我也想说,当数据比较棘手,矩阵很奇异或理论不为人所知时,您可以不使用OLS。
感谢
eavprog的初始消息。
再见!