前言

除了我最近的文章，我还想谈谈MU（多用户）MIMO的话题。我已经提到过Haardt教授的一篇非常著名的文章，他与他的同事一起提出了一种基于线性方法（即通道的对角线化）的下行链路中用户分离算法。这篇文章被大量引用，并且是其中一项考试作业的基石出版物。因此，为什么不弄清楚所提出算法的基础呢？

问题陈述

首先，让我们决定我们现在将在MIMO主题的哪个区域工作。
常规上，MIMO技术框架内的所有传输方法可以分为两个主要组：

空间多样性

主要目标是提高传输的抗干扰能力。如果简化了空间信道，则它们彼此重复，因此，我们可以获得最佳的传输质量。

范例：
-分组代码（例如Alamuti方案）；
-基于维特比算法的代码。

空间复用

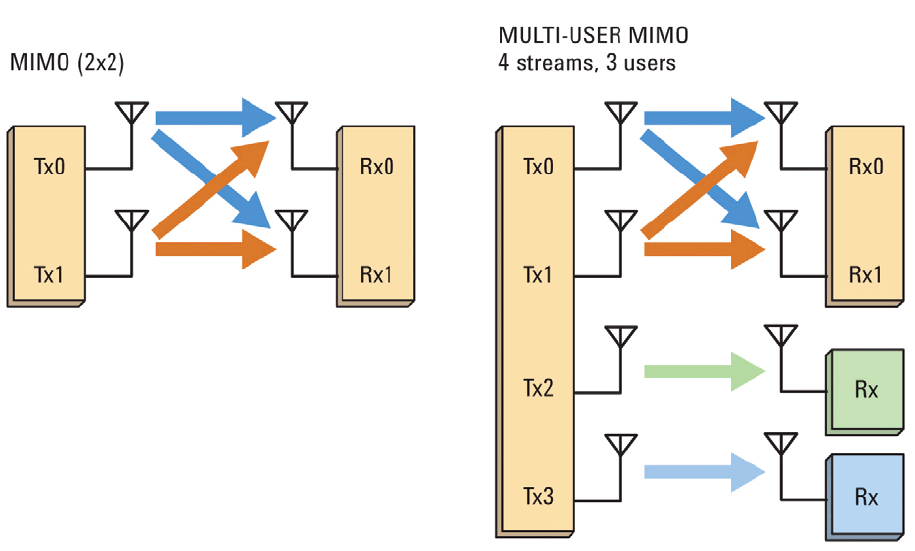
主要目的是提高传输速度。我们已经在上一篇文章中讨论过，在某些条件下，MIMO信道可以视为一系列并行SISO信道。实际上，这是空间复用的中心思想：实现最大数量的独立信息流。在这种情况下，主要问题是抑制信道间干扰（信道间干扰） ，对此存在几种解决方案：

-水平通道分离；
-垂直（例如，V-BLAST算法）；
-对角线（例如，D-BLAST算法）。

但这当然不是全部。

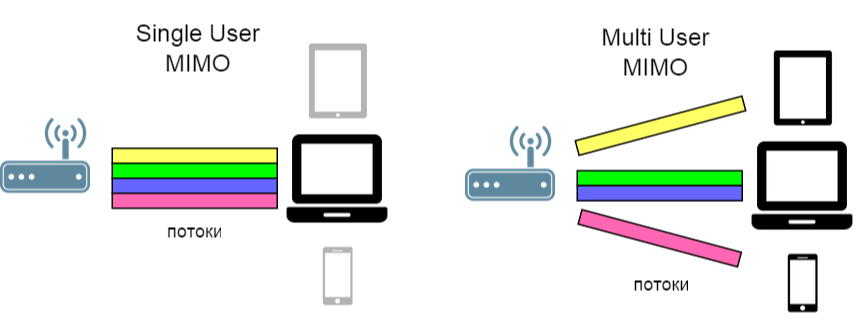
空间复用的思想可以扩展：不仅划分信道，而且划分用户（SDMA-空分多址）。

（链接到插图来源）

因此，在这种情况下，已经有必要对抗用户间的干扰 。为此，提出了一种称为块对角化零强迫的算法，我们今天正在考虑该算法。

数学描述

让我们像以前一样从接收信号模型开始。更确切地说，我们在图上显示了什么以及来自何处：

在这种情况下，通道矩阵的形式为：

$\ underset {M_R \ times M_T} {\ mathbf {H}} = \开始{bmatrix} \ underset {M_ {R1} \ times M_T} {\ mathbf {H} _1} \\ \ underset {M_ {R2} \次M_T} {\ mathbf {H} _2} \\。 \\。 \\。 \\ \下陷{M_ {RK} \乘M_T} {\ mathbf {H} _K} \ end {bmatrix} \ qquad（1）$

与发射天线总数 M_T ，以及接收天线总数 $M_R = \ sum_ {k = 1} ^ K M_ {Rk}$ 。

重要事项 ：
仅当发射天线的数量大于或等于接收天线的总数时，才能应用此算法：
$M_R \ leq M_T$

此条件直接影响对角化的属性。

因此，可以将接收到的符号（信号）模型以矢量形式编写为：

$\ mathbf {r} = \ mathbf {D} \左（\ mathbf {H} \ mathbf {F} \ mathbf {s} + \ mathbf {n} \ right）\ qquad（2）$

但是，查看特定用户的公式会更有趣：

$r_k = \ mathbf {D} _k \ left（\ mathbf {H} _k \ mathbf {F} _k s_k + \ mathbf {H} _k \ sum_ {i = 1，i \ neq k} ^ K \ mathbf {F} _i s_i + n_k \右）\ qquad（3）$

实际上：

$\ mathbf {H} _k \ mathbf {F} _k s_k$ 对第k个用户来说是有用的信号，
$\ mathbf {H} _k \ sum_ {i = 1，i \ neq k} ^ K \ mathbf {F} _i s_i$ -这是来自其他用户的干扰，

-加性噪声。

所以我们来制定主要任务：

你可以找到这样的矩阵 $\ mathbf {F}$ 这样干扰部分变为零！

这就是我们要做的。

算法说明

我们将通过一个示例进行描述，并作为示例，我将给出一些第一手截图，并对它们进行一些评论。

考虑第一个用户：

让我们谈谈主要步骤：

我们做一些矩阵 $\ mathbf {\帽子{H} _1}$ 来自所有其他用户的渠道矩阵。

我们使用SVD方法分解它。
在矩阵中 $\ mathbf {\帽子{V} _1}$ 我们找到了噪声子空间（null-subspace）-矩阵 $\ mathbf {\帽子{V} _1 ^ {（0）}$ （即超出矩阵范围的所有内容 $\ mathbf {\帽子{H} _1}$ -表示它）
我们从这个噪声矩阵及其Hermitian共轭组成一些投影矩阵 $\ mathbf {P_1}$ 。

继续：

现在通道矩阵的原始部分 $\ mathbf {H} _1$ 与结果投影矩阵相乘 $\ mathbf {P} _1$ 。
我们通过SVD分解结果。
在矩阵中 $\ mathbf {V_1} ^ H$ 选择行在哪里 -等级 $\ mathbf {H} _1 \ mathbf {P} _1$ 。
转置它们并获得矩阵 $\ mathbf {F} _1$ （或 $\ mathbf {M} _1$ -如所示）。

因此，将对每个用户重复此过程。这不是数学的魔力：使用线性代数的方法，我们可以完全解决技术问题！

请注意，实际上，不仅使用获得的预编码矩阵，还使用后处理矩阵和奇异值矩阵（请参见幻灯片）。后者例如用于根据已知的注水算法来平衡功率。

我们对算法建模

我认为进行小型模拟以合并结果并不是多余的。为此，我们将使用Python 3，即：

import numpy as np

用于基本计算，以及：

 import pandas as pd

显示结果。

为了不堆积，我将源放在这里

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF

假设我们有8个发射天线，而3个用户分别有3、2和3个接收天线：

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt)

我们初始化我们的类并应用适当的方法：

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices()

我们带来一种可读的形式：

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0

并且让我们稍作澄清（尽管您可以没有它）：

 print(pd.DataFrame(np.round(np.real(df),100)))

您应该得到这样的内容：

实际上，这里是块，这里是对角线。并将干扰降到最低。

这样的事情。

文学作品

Spencer，Quentin H.，A。Lee Swindlehurst和Martin Haardt。 “用于多用户MIMO信道中下行链路空间复用的零强制方法。” IEEE关于信号处理的事务52.2（2004）：461-471。
马丁·哈德（Martin Haard）“ 多用户MIMO系统的鲁棒传输处理 ”

聚苯乙烯

在我的母语专业的老师和学生友爱中，我问好！

MU-MIMO：实现算法之一

前言

问题陈述

数学描述

算法说明

我们对算法建模

文学作品

More articles: