多年来,我一直在为数学和计算机科学家的学生开设组合图和图形课程(俄语在俄语中是计算机科学家)?以前是在学术大学,现在是在
圣彼得堡国立大学 。 我们的程序的设计方式是将这些主题作为“理论计算机科学”的一部分(其中的其他主题是算法,复杂性,语言和语法)。 我不能说形而上学或历史学的合理性:尽管如此,组合对象(图形,集合系统,排列,方格图等)在计算机问世之前就已经开始研究,而后者虽然很重要,但仍不是引起人们兴趣的唯一原因。他。 但是令人惊讶的是,经常看到组合技术和理论计算机科学领域的专家:Lovas,Alon,Semeredi,Razborov等。 这可能是有原因的。 在我的课程中,奥林匹克编程冠军通常会为复杂的问题提供非常平凡的解决方案(我不会列出它们,任何想了解顶级编解码器的人。)总的来说,我认为社区中可能会涉及组合技术。 说出是否是这样。
让您需要构建从1到数字的随机排列
$内联$ n $内联$ 这样所有排列都是同等可能的。 这可以通过多种方式完成:例如,首先随机选择第一个元素,然后从其余的第二个元素中依次类推。 或者,您也可以这样做:随机选择点
$ inline $ t_1,t_2,\ ldots,t_n $ inline $ 在细分中
$内联$ [0,1] $内联$ ,并查看其订购方式。 用1替换最小的数字,用2替换第二个数字,依此类推,我们得到一个随机排列。 容易看到的一切
$ inline $ n!$ inline $ 排列也同样可能。 有可能,不在细分中
$内联$ 0.1 $内联$ 选择点,例如,从1到1
$内联$ n $内联$ 。 巧合在这里是可能的(对于段来说,它们也是可能的,但是可能性为零,因此它们不会打扰我们)-您可以用不同的方式处理它们,例如,对重合数字进行重新排序。 或者,将
N取大些,以使重合的可能性较小(
$内联$ N = 365 $内联$ 和
$内联$ n $内联$ 您班上的学生人数很多,我们在谈论两个生日的巧合。)这种方法的一种变化:随机记录
$内联$ n $内联$ 在单位正方形中点,并查看其坐标相对于横坐标的排序方式。 另一个变化:在细分中标记
$内联$ n-1 $内联$ 指出并查看将其划分为段的长度的顺序。 这些方法的关键是测试的独立性,根据测试的结果可建立随机重排。 安德烈·尼古拉耶维奇·柯尔莫哥洛夫(Andrei Nikolaevich Kolmogorov)说,概率论是一种度量加独立性的理论-任何处理过概率论的人都会证实这一点。
我将使用
树的钩子公式示例来说明这有何帮助:
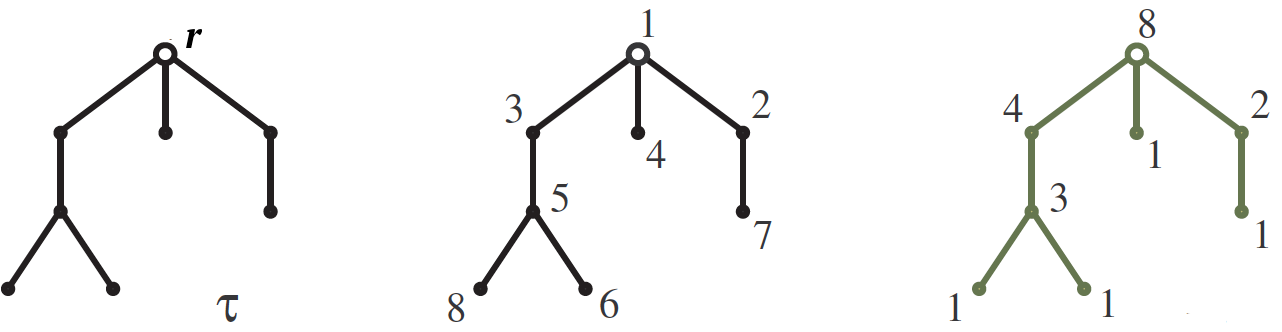
让
$ inline $ \ tau $ inline $ -被根暂停
$内联$ r $内联$ 与树
$内联$ n $内联$ 如图所示,山峰逐渐下沉。 我们的目标是计算数量
$内联$ S(\ tau)$内联$
编号树顶
$ inline $ \ tau $ inline $ 从1到1的数字
$内联$ n $内联$ 这样,对于每个边缘,其顶部的数字大于底部的数字。 这些数字之一显示在中间的图片中。 答案是使用
钩子尺寸来制定的。 钩子
$内联$ H(v)$内联$ 高峰
$内联$ v $内联$ 我们称从该顶点开始生长的子树,其大小就是其中的顶点数。 钩的长度写在右图中相应顶点的旁边。 所以,数字的数量是
$ inline $ n!$ inline $ 除以钩子尺寸的乘积,因此在我们的示例中
$$显示$$ S(\ tau)= \,\ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210。 $
我们可以用不同的方式证明该公式,例如通过对顶点数量的归纳来证明,但是我们对随机排列的看法使我们无需进行任何计算即可进行证明。 它不仅好于优雅,而且还因为它很好地概括了关于用规定的不等式进行编号的更微妙的问题的事实,而不是现在更好。 因此,取
n个不同的实数并将它们随机放置在树的顶部,每个实数都有一个,
$ inline $ n!$ inline $ 排列也同样可能。 对于每个边缘,边缘顶部顶点处的数字大于其底部顶点处的数字的可能性是多少? 答案是:
$内联$ S(\ tau)/ n!$内联$ ,并且它不依赖于一组数字。 如果不依赖于此,那么我们考虑一下也是随机选择的数字(为了确定性)
$内联$ [0,1] $内联$ 。 不必先随机选择数字,然后将它们随机排列在树的顶部,我们可以简单地在每个顶点上随机且独立地选择一个数字:它们的重新排列将自动进行。 这样
$内联$ S(\ tau)/ n!$内联$ 这是随机独立数的概率
$内联$ \ xi(v)$内联$ 为每个顶点选择一个
$内联$ v $内联$ 木
$ inline $ \ tau $ inline $ ,形式的所有不等式
$内联$ \ xi(v)> \ xi(u)$内联$ 对于所有边缘
$内联$ v \到u $内联$ ,
$内联$ v $内联$ 是肋骨的顶部顶点,并且
$内联$ u $内联$ -底部。 我们以等效形式来公式化这些条件,但方式略有不同:对于每个顶点
$内联$ v $内联$ 这样的事件应该发生-我将指定它
$内联$ Q(v)$内联$ :号
$内联$ \ xi(v)$内联$ -钩子树的顶点处所有数字中的最大值
$内联$ H(v)$内联$ 。
注意
$ inline $ \ frac {1} {| H(v)|} $ inline $ 这是事件的可能性
$内联$ Q(v)$内联$ 。 其实在钩子上
$内联$ H(v)$内联$ 可用
$ inline $ | H(v)| $ inline $ 顶点和最大挂钩数以相等的概率映射到它们的每个顶点
$ inline $ \ frac {1} {| H(v)|} $ inline $ 。 所以勾子公式
$ inline $ S(\ tau)/ n!= \ prod_v \ frac {1} {| H(v)|} $ inline $ 可以表述为:所有事件一次发生的概率
$内联$ Q(v)$内联$ 等于这些事件的概率乘积。 造成这种情况的原因可能有很多不同,但是想到的第一个在这里起作用:这些事件是独立的。 为了理解这一点,让我们看一个事件
$内联$ Q(r)$内联$ (对应于根)。 它包含以下事实:根中的数字大于顶点中的所有其他数字,并且其他事件与未写入根中的数字之间的比较有关。 那是
$内联$ Q(r)$内联$ 关于数量
$ inline $ \ xi(r)$ inline $ 以及在其他顶点处
的数字
集 ,而所有其他事件在除根节点之外的其他顶点处
的数字
量级均如此 。 正如我们已经讨论的那样,“顺序”和“众多”是独立的,因此事件
$内联$ Q(r)$内联$ 独立于他人。 顺着这棵树,我们发现所有这些事件都是独立的,与所需事件无关。
通常,钩子的公式是不对树中的顶点进行编号,而是
对杨图中的单元进行编号的公式
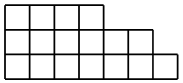
沿坐标轴方向增加,并且钩子比树上的钩子更像钩子。 但是事实证明,该公式更加复杂,值得单独介绍。
顺便说一句,我不禁谈论
随机杨氏图的模型。 年轻的图是这样的人物
$内联$ n $内联$ 单位平方,其行的长度从下到上增加,列的长度从左到右。 杨氏面积图的数量
$内联$ n $内联$ 被指示
$内联$ p(n)$内联$ ,此
重要函数的行为很有趣且与众不同:例如,它的增长速度快于任何多项式,但慢于任何指数。 因此,尤其是,生成随机的Young图(如果我们需要所有面积图
$内联$ n $内联$ 同样有可能
$内联$ 1 / p(n)$内联$ )并不是一件小事。 例如,如果您一次添加一个单元格,选择一个随机添加的位置,则不同的图表将具有不同的概率(因此,单线图表的概率等于
$ inline $ 1/2 ^ {n-1} $ inline $ 。)事实证明,在图表上很有趣,但是并不一致。 可以如下获得均匀性。 拿号码
$ inline $ t \ in(0,1)$内联$ ,就我们而言,该区域中的数字最适合
$内联$ 1- \ mathrm {const} / \ sqrt {n} $内联$ 。 对于每个
$ inline $ k = 1,2,\点数$ inline $
考虑均值非负整数的几何分布
$内联$ t ^ k $内联$ (即数字的概率
$ inline $ m = 0,1,\点数$ inline $ 等于
$ inline $ t ^ {km}(1-t ^ k)$ inline $ ) 我们根据它选择一个随机变量
$内联$ m_k $内联$ (有很多方法可以组织此操作)。 大体上
$内联$ k $内联$ 最有可能是0。让我们看一下其中的Young图
$内联$ m_k $内联$ 行是长度
$内联$ k $内联$ 在每个
$ inline $ k = 1,2,\点数$ inline $ 。 之所以称其
为ship方法,是因为总面积
有时等于
$内联$ n $内联$ 。 如果不相等,则重复实验。 实际相等
$内联$ n $内联$ 她经常选择精明
$ inline $ t \ in(0,1)$内联$ 。 我邀请读者独立证明给定区域的所有图都是同等可能的,并估计步骤数。