2019年3月29日-首席研究员Michael Trott
参赛作品
在所谓的“新SI”（
国际单位制的
更新版本）中 ，它将确定七个基本计量单位（秒，米，千克，安培，开尔文，摩尔和坎德拉），并将于2019年5月20日生效，所有SI单位将为通过基本物理常数的精确值确定。 结果，所有上述SI单位（牛顿，伏特，欧姆，帕斯卡等）最终将用基本常数表示。 （最后，基本物理学将真正控制我们的日常生活lives）
下表显示了从今年5月20日星期一晚上到5月21日星期二早上一切将如何变化。
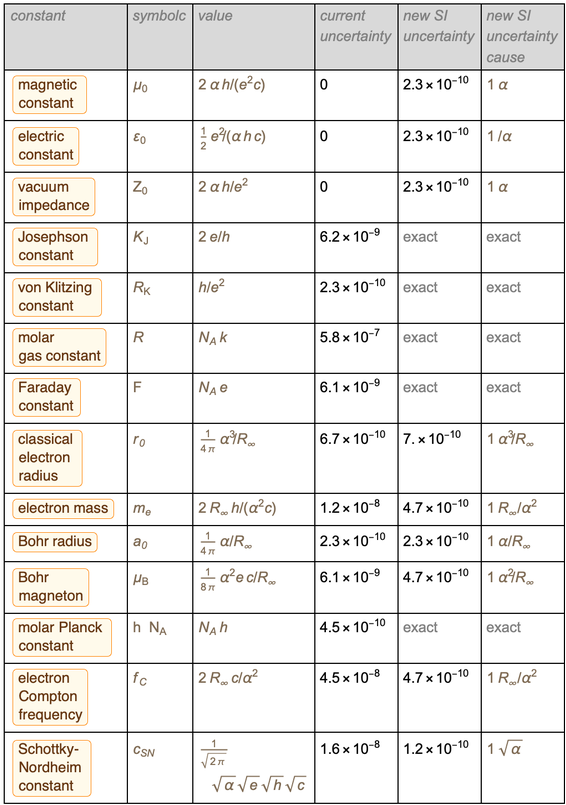
从此表中计算数据是此博客的目标。 因此，让我们从新的SI的简要概述开始。
除了众所周知的光速精确值外，在四个星期内，还有四个物理常数-普朗克常数，玻尔兹曼常数，阿伏加德罗常数和密立根常数（通常称为基本电荷）-将具有精确值。 这项更改的决定是去年11月在国际上做出的（我在上一期中对此进行了评论
博客）。
以下是当前
SI手册草案第12页的摘录。
请注意，在这些定义中，十进制数字是指精确的十进制数字，而不是指计算机上具有有限精度且不是精确数字的机器编号。 如今，Cs-133分裂式超细结构中的跃迁频率，光速和“光效率”已经有了确切的数值。
世界讨论未来的变化
这种变化将对其他物理常数产生一些有趣的结果：一些当前测量且有误差的常数将变得准确，而一些当前准确的常数将在未来具有近似值且有限误差。 这些更改是不可避免的，以保证整个系统的一致性。
今年第一期
的《世界物理学》在威廉·霍夫（William Hough）
给编辑的
信中谈到了这个问题。 他写道：
通过将电荷固定在电子（ e ）和普朗克常数（ h ）上，所有物理单位现在都“永生在石头中”，这非常好。 但这提出了一个尴尬的问题。 优良的结构常数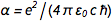 
其中c是光速， 
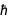是的 
。 从熟悉的方程式 
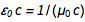和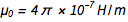 
我们很快发现 
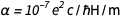。 当然，这是一个无量纲的纯数字，现在永远固定为等于1 / 137.13601，非常接近可接受的值。 这并不奇怪，因为后者的值将用于e和the的商定新值中。 但是自然有其自身的价值，目前我们还不知道，因此，它在钻石中具有无限的价值。 暗示我们比自然更了解我们可以原谅。 但是，如果宇宙的未来理论被接受并给出确切含义，该怎么办？ 
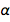哪个与可接受的值有显着不同？ 这会发生吗？ 已经尝试寻找α的理论值，但是它们包括威胁性和有争议的量子电动力学。
问题是在新的SI系统中
和
现在将具有不正确的值，并带有一些错误。 在此博客中，我们将使用Wolfram语言及其对物理单位和常数的了解来了解这些以及其他物理常数如何获得（或丢失）错误，以及为什么这是定义基本单位的数学结果。
有关Wolfram语言成分的简要概述
Wolfram语言是进行数值实验和符号计算，识别可能后果的独特媒介。 除了一般的计算功能外，三个系统组件在这里也非常有用：
1）Wolfram语言的单位和物理量的结构。
经典单位（例如米，英尺等）可用于计算和可视化。 并且，当然是在计量单位的转换中。
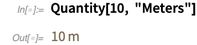
由于两个单位的比率定义明确，因此转换为普通的美国单位会产生分数（而不是实数的近似值！）。
物理学家（尤其是）喜欢使用“自然”单位。 通常，这些自然单位仅仅是物理常数或其组合。 例如，光速（此处使用自然语言输入）。
以SI单位表示（因为这是速度，因此需要以米和秒为单位），因此光速具有准确的值。
另一方面，普朗克常数当前没有确切值。 因此，它的值以SI基本单位表示，是一个近似的十进制数。
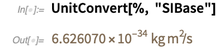
请注意，精度6.626070 ...反映了已知数字的数量。
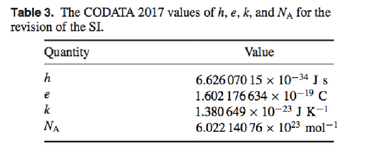
这是在
CODATA 2017中发布的普朗克常数的最后一个建议值，以准备常数的完善。 下面是相应的表：
连接两个物理量的物理常数（或其组合）通常可以用作自然单位。 最简单的示例是按照光速测量速度或以terms表示微观扭矩。 或能量可以用隐含因子来衡量
。
DimensionalCombinations函数可用于搜索物理常数的组合，这些组合允许您关联两个给定的物理量。 例如，可以建立质量与能量之间的以下关系：
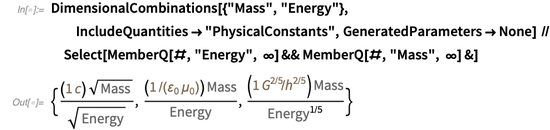
第一个平等反映了爱因斯坦的著名公式
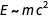
，第二个等效于第一个关系，而第三个-（在尺寸上）表示
。
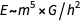
2）实体类“
PhysicalConstant ”最近添加到
Wolfram知识库中 。
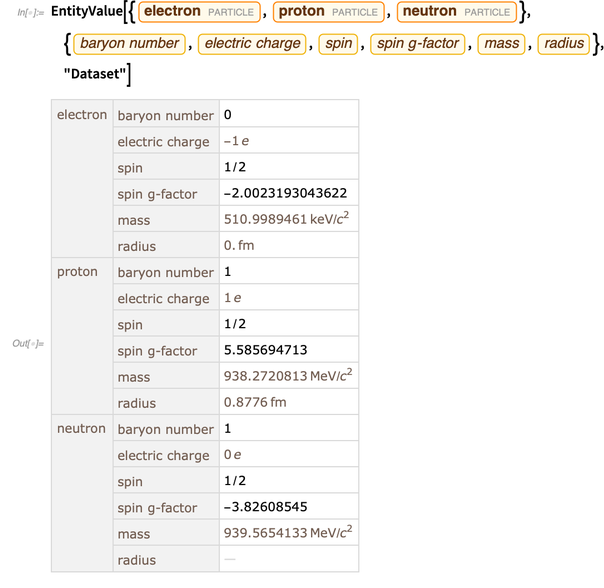
Wolfram语言中的函数和对象是“计算产生的”，即它们已准备好用于计算。 但是要描述和模拟真实世界，您需要有关真实世界的数据。 实体结构是获取此类数据的便捷且完全集成的方式。 以下是有关电子，质子和中子的一些数据。
新的实体单位之一是物理常数。 当前，知识库包含250多个物理常数。
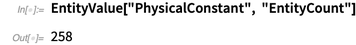
以下是十二个随机选择的示例。 此外，没有明确定义什么常数是物理常数，基本粒子的质量，标准模型的拉格朗日参数等。为方便起见，该列表还包含根据天文历书的
天文常数 。
在Jean-Marc Levy-Leblond的著名
著作中，大多数基本物理常数被称为C类常数，以下是C和B类常数。
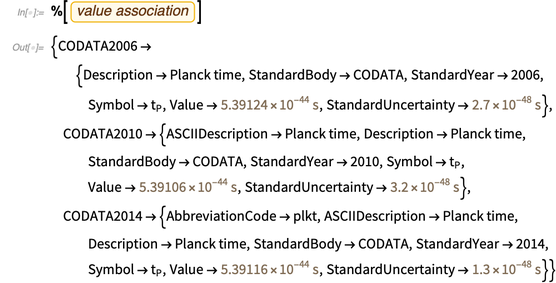
以自然时间单位普朗克时间为例。 使用
ToEntity和
FromEntity函数可以轻松地在以单位为单位的物理常数和以实体为单位的物理常数之间来回移动。 下面说明对应于普朗克时间单位的实体。
知识库包含有关他的大量元信息，例如，最新的CODATA列表中的值。
最后一个包含意义和错误的结论将我们引向第三个重要功能，该功能将在以后有用：
3）在Wolfram语言的版本12中引入了
Around []函数。
Around []函数提供的值不正确，表示平均值和错误。 []
周围的算术模型基于
GUM （表达测量误差的指南）-不要与Leibniz Plus-Minus-calculus混淆。 这是带有错误的值。
使用有错误的值进行计算的最重要和最有用的方面是它们考虑了相关性。 在算术数或区间中天真地使用此类值可能会低估或高估所产生的误差。
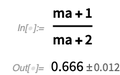
在下面，我们看到
AroundReplace []函数将相关性考虑在内。
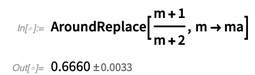
回到致编辑的信
现在，让我们使用这三个组件以及更详细的William Hough给编辑的信。
在
e和
and的当前近似值
下 ，精细结构常数的这两个值在其误差范围内保持一致。 第一个是从字母到编辑器的表达式，第二个是数量（
Quantity []），它表示精细的结构常数。
每隔几年，CODATA都会发布基本常数的官方值（请参见
精细结构常数 ）； 就像我说的那样，Wolfram语言中使用的值是最新的CODATA值，最终的错误反映在数字的准确性上。
请注意，直接测量的精细结构常数比通过其他常数表示精细结构常数的精确度稍高。
如果我们使用即将到来的
e和
exact的精确值，
并使用当前的精确值
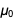
，我们以以下形式获得精细结构常数的以下精确值：
。
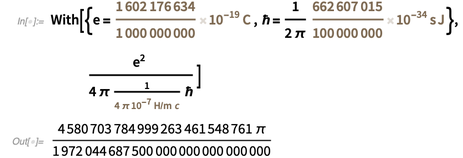
甚至不
玩骰子的主，不太可能选择这样的数字作为值
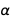
在我们的宇宙中。 这意味着尽管
e和
ℏ在新的SI中固定，但当前的精确值
和
必须不可避免地“脱钩”（另请参阅Goldfarb关于数量的
文章 新SI）。 （我们将回到为什么
和
很快就会变得不准确。）
这意味着，在今年5月20日之后，这些结果将不同于下面给出的结果。
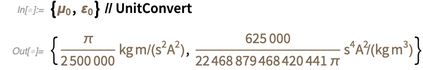
（在简短说明中，实体类“
PhysicalConstant ”也具有常量的估计值，例如精细结构常量）：
现在，除了关于精细结构常数的确切形式的神学论证之外，从物理角度来看，为什么
和
应该是不正确的？ 作为概率的论证，让我们考虑
。 最杰出的结果之一是库仑定律。
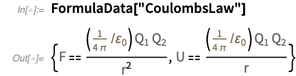
在
现有的 SI系统中，安培具有“精确”定义：
安培是直流电，如果将其支撑在两个无限长且横截面略为圆形的平行导体中，并置于真空中1米的距离，则会在这些导体之间产生等于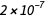 
牛顿每米长度。 该定义使用的是纯机械量的牛顿和米（即膨胀后，秒，米和千克）。 与电子的电荷没有关系，在现有的SI系统中，基本电荷是实验测量的量。
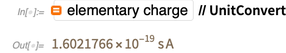
多年来，该实验测量值已经发生了变化，变得更加准确。
库仑定律左侧的力（以牛顿表示）包含千克的基本单位，在普朗克常数的值变为恒定值之后，千克的基本单位也可以精确定义。 由于没有理由相信所有自然定律都可以用有限有理数表示，因此库仑定律中唯一可能的“运动部分”将是
。 必须确定其数值，并使库仑定律的左右两侧重合。
从物理学的更基本的角度来看，精细的结构常数是相互作用常数，它决定了电磁相互作用的强度。 而且，也许有一天，物理学可以计算出精细结构常数的值，但是我们离这一点还差得很远。 仅选择单位定义并不能确定价值
。
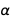
都是真的
和
变得不固定，还是有可能使其中之一保持准确？ 由于光速和比例已经很准确
如果其中之一
或
准确，其他也必须准确。 我们知道至少有一个必须不提交，因此可以肯定两个都必须不提交。
现在，由普朗克常数，玻尔兹曼常数，阿伏伽德罗常数和基本电荷给出的值既不是任意的，也不是完全定义的。 最多可以确定8个字符，因此5月20日之后确定的度量单位与5月20日之前确定的单位的“大小”相对应。 但是未定义右下角的数字。 因此，基本电荷的将来精确值的值可以是
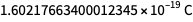
但不是
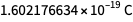
。 奥卡姆（Occam）的剃刀和理性使我们能够使用
。
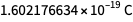
从技术上讲，以前计算中的替代是通过
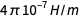
在公式中
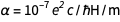在重新定义之前使用了amp （请记住
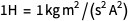
），但也使用了基本电荷的确切值，即重新定义后的安培定义。 而且，我们始终需要停留在一个单位制中。
误差优化表格的计算
因此，自然而然地出现了一个问题：这些“不确定的”含义应该是什么？ 在上一个博客中，我手动创建了一个新值
。 可以手动完成的操作可以使用计算机程序完成，因此让我们实现一个小程序，该程序可以计算物理常数的导数的错误优化形式。 在面向未来的方法中，定义了新SI的七个常量的实体类已经可用。
以下是在新的SI中具有确切值的常数。
这些常量的当前值及其误差（使用
Around []函数计算）具有以下形式：
使用实体类“
PhysicalConstant ”，我们可以获得新的，即将到来的物理量值。 请注意，就像在所有计算机语言中一样，精确整数和有理数是显式整数或有理数（但不是十进制）。
许多物理常数可以通过各个物理领域的物理理论给出的方程来关联。 将来，我们希望将自己局限于基本的电磁现象理论，在该理论中，常数的误差将减小为精细结构常数的误差。
和里德伯格常数
。 例如，如果我们包括重力现象，我们将不得不使用独立测量的重力常数G，尽管它具有很大的误差（这就是NSF遭受所谓的“
大G挑战 ”的原因）。
此外，我们将自身限制为电，磁和质量，其误差减少为单位
和
。
下面我们使用新的
Around函数来表达带有相应错误的值
和
。
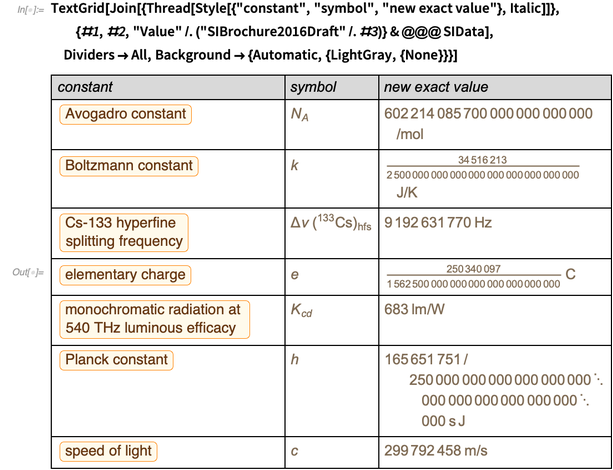
目前，根据CODATA 2014，相对误差为
关于
和
关于
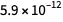
。 如您所见，该错误为
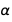
超过
。
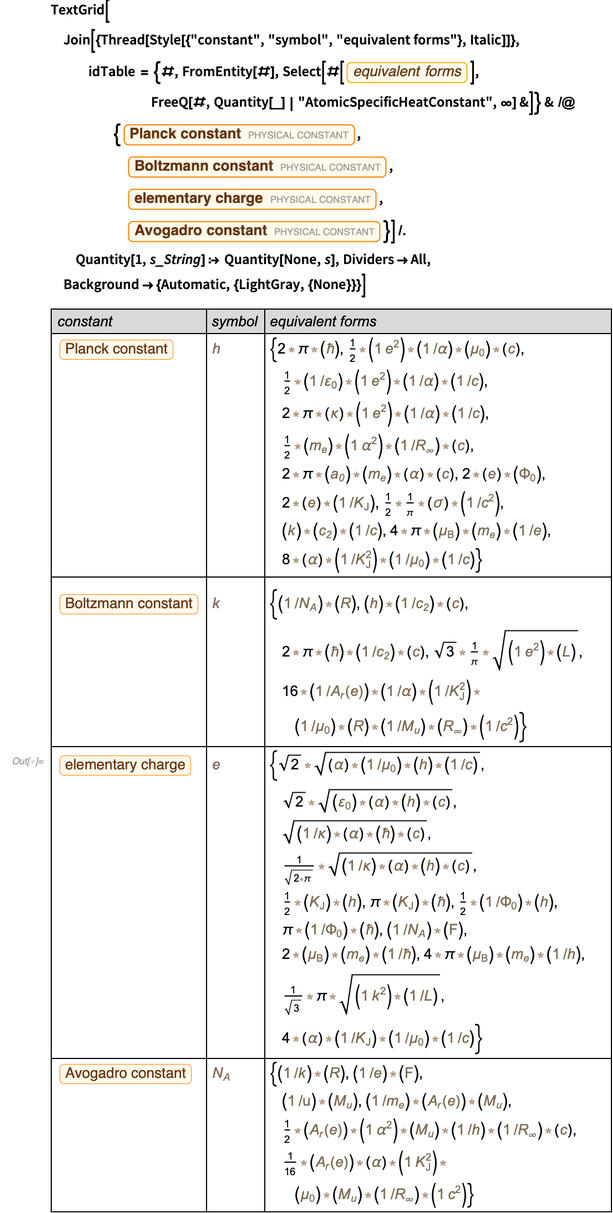
下图是log-base-10相对误差的图表
作为函数
a和
b 。 显然，在很小的程度上，乘积的相对误差弱地取决于指数
a和
b 。 该图表明误差的依赖性
相对于（精细结构的指数）占优势。 里德伯格常数的误差比精细结构常数的误差小50倍，这一事实解释了这一发现。
要计算新SI中各种常数的误差，我们将使用以下步骤：
•检索可从
PhysicalConstant实体类访问的物理常数的等效表示形式。
物理常数之间的这些相同相等性是物理定律，因此在新旧SI中均应保留。
•将公式视为一组代数等式，通过将新SI的七个基本常数以及精细结构常数结合起来，可以使用各种排除方法来表示一个常数
和里德伯格常数
。
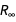
这些是我们允许在所考虑的每个新常数的定义中应用的九个基本常数。 （从技术上讲，列表中有10个常量，但是由于
h和
between之间的简单比例关系，因此该列表中实际上有9个“不同”常量。）
实体类“
PhysicalConstant ”包含许多有关物理常数之间关系的信息。 例如，这是当前正在测量的四个常数的等效形式，并将很快被识别为具有精确值。
在测量值的精度范围内，所有这些单位元素现在都可以工作。 这是普朗克常数其他形式的快速数值检查。 但是具体的数值，尤其是误差，取决于实际的表示形式。
使用Around []，我们可以轻松计算出结果错误。
. .
, . , ? , , , , , .
, , ( ,
实体 [“ PhysicalConstant” ，。]和数量 [ 1 ，。]等于）。我们使用实体而不是随后的计算中的数量的原因有两个方面：首先，实体是方便且易于阅读的表示形式；其次，代数函数（例如GroebnerBasis）不会渗透数量来确定其第一个参数的性质。
然后我们将所有恒等式设为多项式。 最后一步是：（1）从右侧减去左侧； （2）不再出现常数的小数幂（例如平方根）。 通过查找所有分数指数并找到所有分母的LCM（最小公因数），我们可以将其转换为多项式。
下面是以前的方程式之一，其中包含具有小数幂的常数。
经过多项式化之后，我们得出了存在的三个常数中几个变量的多项式。 这些多项式必须消除。
下表演示了
toPolynomial函数如何应用于前面所示的基本电荷等效形式。 ℏ规范化后
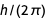
，某些结果多项式变得相同。
现在，基于可用的物理常数（没有在新SI的定义中使用的常数），我们获得了足够的等价形式来创建一组方程。
以下是获得的用于表示基本电荷的多项式方程式的列表。
我们通过错误表达所有错误
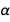
和
。 仅这两个常数足以表示许多物理常数的误差。 并且由于它们的误差彼此独立，并且误差非常小，因此这两个众所周知的常数最适合表示许多物理常数的优化版本（在误差的意义上）。 并且，当然，我们允许新SI中的所有七个精确常数； 因为它们是准确的数量，所以它们的存在不会改变错误。
关于以SI常数和SI常数表示给定常数的主要工作
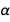
和
将由
GroebnerBasis函数实现。 设置
MonomialOrder-> ElventionOrder参数是至关重要的步骤，该步骤将删除所有“不必要的”物理量，从而为一个多项式方程式保留精确定义的常数以及（如有必要）精细结构和Rydberg常数。
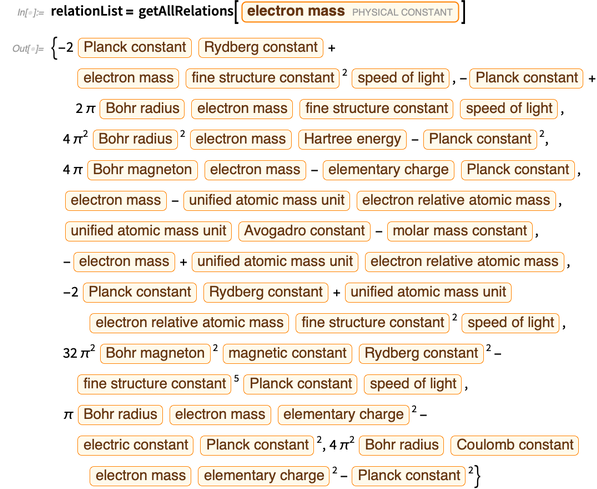
通过消除受电子质量限制的常数，我们得到
。
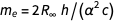
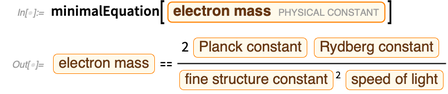
该表达式的错误源于
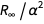
。 我们可以定义一个删除成员的函数
导致错误。
为了更简洁地表示，我们可以定义一个函数，该函数以字符串形式返回等效形式以及旧的和新的错误。
在博客的结尾，我们提供了一个针对多个物理常数的新旧错误表。 选择此列表作为代表示例； 其他常数可以用类似的方式处理（这可能需要添加其他不精确的常数进行守恒，例如重力常数或标准模型的参数）。
合并表中的行可得到以下结果，以在新的SI单位系统中以最佳方式表示这些常数。
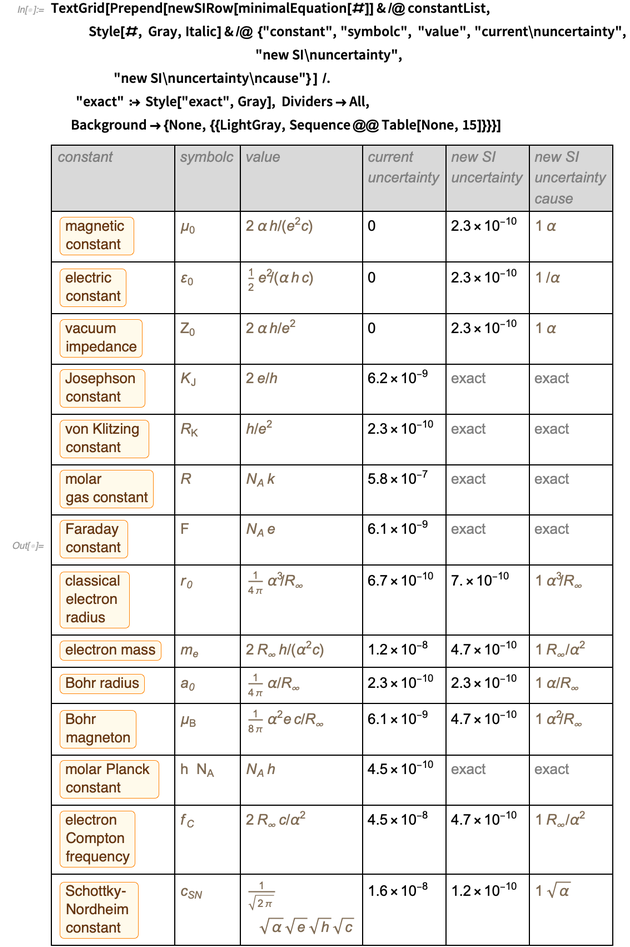
这是我们想要显示的表，我们设法显示了它。 注意外观
在分子和分母中
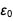
和
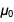
这样在减少结果之后
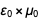
变成
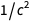
。 在
重新定义SI单位的Wikipedia页面的底部可以找到类似的列表。
现在我们可以冷静地期待
2019年世界计量日 ，通过基本常量来描述一个从根本上更好的世界。
下载
Wolfram笔记本博客。
免费的临时Wolfram Mathematica系统有问题吗？ 联系info-russia@wolfram.com