📯 🔶 💂 小波分析第1部分 🧚🏾 👨🏿‍🤝‍👨🏾 👩‍🌾

引言

考虑在PyWavelets PyWavelets 1.0.3库中实现的离散小波变换（DWT）。 PyWavelets是根据MIT许可发布的免费开源软件。

在计算机上处理数据时，可以执行连续小波变换的离散化版本，其基本内容在我的上一篇文章中进行了介绍。然而，以任意步长Δa和Δb指定小波的参数（a，b）的离散值需要大量的计算。

另外，结果是过多的系数，远远超过了原始信号的样本数量，这对于其重构是不需要的。

PyWavelets库中实现的离散小波变换（DWT）为信号分析及其合成提供了足够的信息，同时在操作数和所需的内存方面很经济。

何时使用小波变换而不是傅立叶变换

当频谱固定时，傅立叶变换将很好地工作。在这种情况下，信号中出现的频率与时间无关，并且信号包含信号中任何位置出现的频率xHz。信号不稳定，结果越差。这是一个问题，因为我们在现实生活中看到的大多数信号本质上都是不稳定的。

傅立叶变换在频域中具有高分辨率，而在时域中为零分辨率。我们在以下两个示例中对此进行展示。

上市

import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 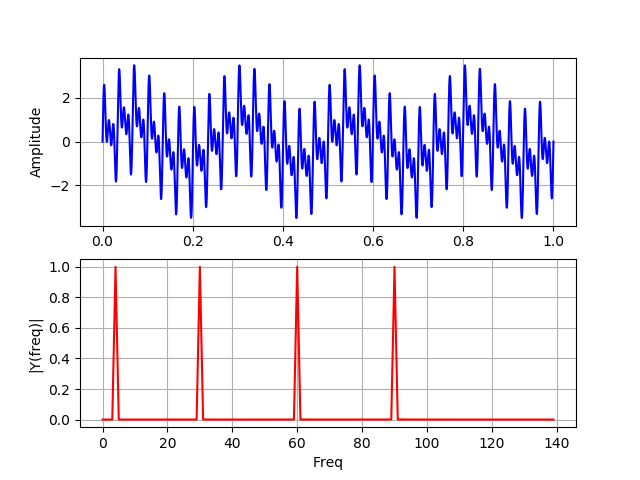sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y= y1a + y2a + y3a + y4a spectrum_wavelet(y) show()

在此图上，所有四个频率在其整个操作期间都存在于信号中。

上市

 import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 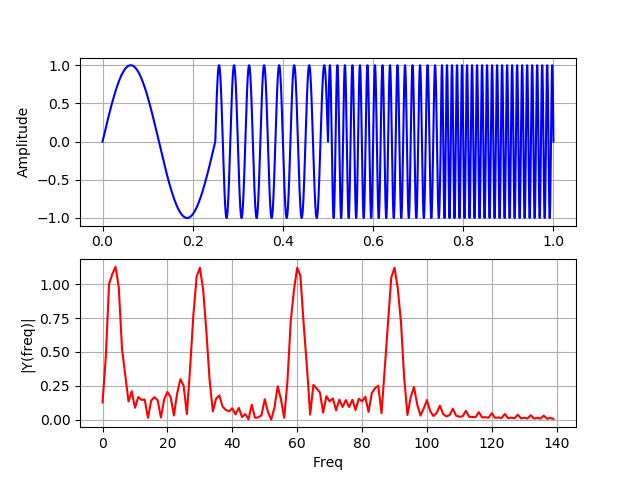sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y = np.concatenate([y1b, y2b, y3b, y4b]) spectrum_wavelet(y) show()

在此图上，信号没有在时间上重叠，旁瓣是由于四个不同频率之间的间隙引起的。

对于包含完全相同的四个峰值的两个频谱，傅立叶变换无法确定这些频率在信号中的位置。分析动态频谱信号的最佳方法是小波变换。

小波的主要特性

小波类型的选择以及因此的小波属性取决于分析任务，例如，确定电力行业电流的有效值，高阶Ingrid Daubechies小波提供更高的精度。可以使用以下清单中的pywt.DiscreteContinuousWavelet（）函数获得小波属性：

上市

 import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title("   -  -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title("  - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show()

我们得到：

离散小波-['db5'，'sym5'，'coif5'，'haar']

 Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False

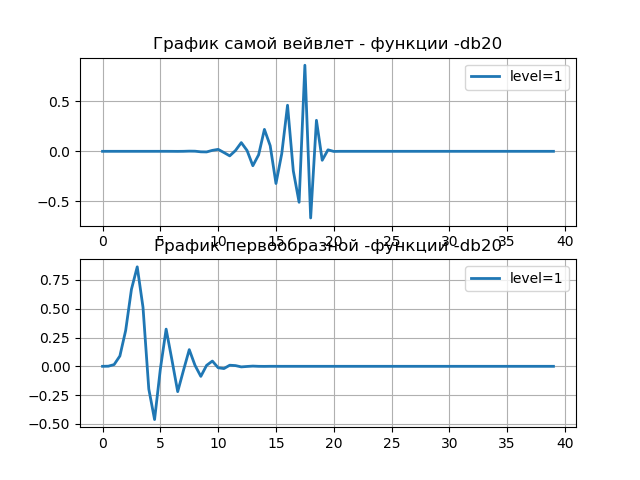
在许多实际情况下，需要获取有关psi小波中心频率的信息-例如，在信号的小波分析中使用此函数以检测齿轮中的缺陷：

 import pywt f=pywt.central_frequency('haar', precision=8 ) print(f) #  : scale=1 f1=pywt.scale2frequency('haar',scale) print(f1)

 0.9961089494163424 0.9961089494163424

使用中心频率

f_{c}

$f_ {c}$ 孕妇小波和比例因子“ a”可以将比例转换为伪频率

f_{a}

$f_ {a}$ 使用公式：

f_{a} = f r a c f_{c} a

$f_ {a} = \ frac {f_ {c}} {a}$

信号扩展模式

在使用滤波器组计算离散小波变换之前，有必要加长信号 。根据外推方法，可能会在信号边界处出现明显的伪像，从而导致DWT变换中的不准确。

PyWavelets提供了几种信号外推技术，可用于最小化这种负面影响。为了演示这种方法，请使用以下清单：

列出信号扩展方法的演示

 import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot # synthetic test signal x = 5 - np.linspace(-1.9, 1.1, 9)**2 # Create a figure with one subplots per boundary mode fig, axes = plt.subplots(3, 3, figsize=(10, 6)) plt.subplots_adjust(hspace=0.5) axes = axes.ravel() boundary_mode_subplot(x, 'symmetric', axes[0], symw=False) boundary_mode_subplot(x, 'reflect', axes[1], symw=True) boundary_mode_subplot(x, 'periodic', axes[2], symw=False) boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False) boundary_mode_subplot(x, 'antireflect', axes[4], symw=True) boundary_mode_subplot(x, 'periodization', axes[5], symw=False) boundary_mode_subplot(x, 'smooth', axes[6], symw=False) boundary_mode_subplot(x, 'constant', axes[7], symw=False) boundary_mode_subplot(x, 'zeros', axes[8], symw=False) plt.show()

这些图显示了短信号（红色）如何扩展（黑色）超过其原始长度。

离散小波变换

为了演示DWT，我们将使用动态频谱的信号，该频谱会随时间增加。信号的开头包含低频值，信号的结尾包含短波范围的频率。这使我们可以通过简单地查看时间轴轻松确定频谱的哪一部分被滤除：

上市

 from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title("     ") ax.plot(chirp_signal) show()

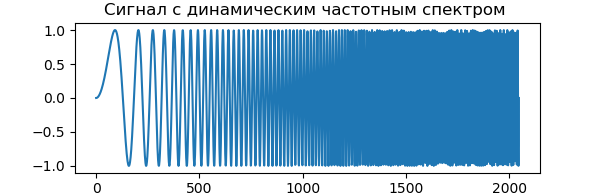
PyWavelets 1.0.3中的离散小波变换是pywt.dwt（）函数，该函数计算矢量指定信号的第一级小波变换的近似系数cA和详细系数cD：

转型一级上市

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show()

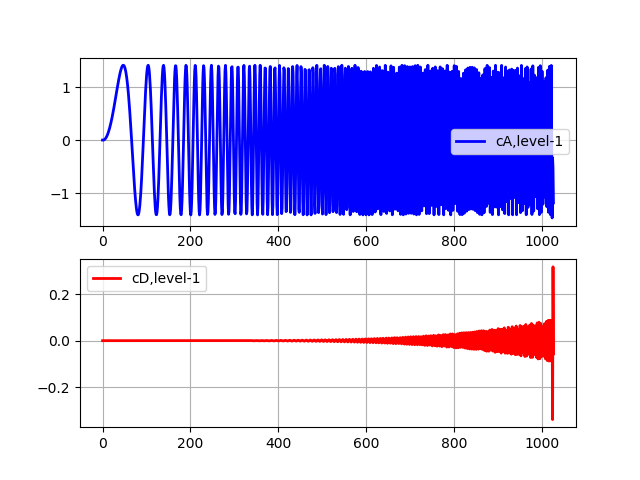
转换级别5清单

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

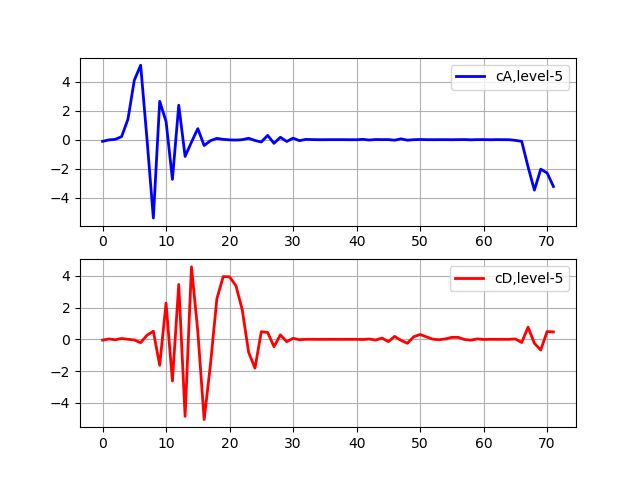
逼近系数（cA）代表低通滤波器（平均滤波器）DWT的输出。细节系数（cD）代表高通滤波器（差分滤波器）DWT的输出。

您可以使用pywt.wavedec（）函数立即计算更高级别的系数。此函数将输入信号和电平作为输入，并返回一组近似系数（第n级）和n组详细系数（从1至第n级）。这是第五级的示例：

 from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

结果，我们得到与上一个示例相同的图。系数cA和cD可以分别获得：

对于cA：

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)

对于CD：

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)

过滤银行

上一节讨论了一些与转换级别有关的问题。但是，DWT始终以高通和低通滤波器的级联形式实现为滤波器组。滤波器组是将信号划分为多个频率子带的非常有效的方法。

在小规模的第一阶段，分析信号的高频行为。在第二阶段，标度以2的倍数增加（频率以2的倍数减少），我们分析最大频率的一半左右的行为。在第三阶段，比例因子为4，我们分析了大约最大频率四分之一的频率行为。这一直持续到我们达到最大分解水平为止。

分解的最大级别可以使用pywt.wavedec（）函数来计算，而分解和细节如下所示：

上市

 import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print('  : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show()

我们得到：

最大分解度：7

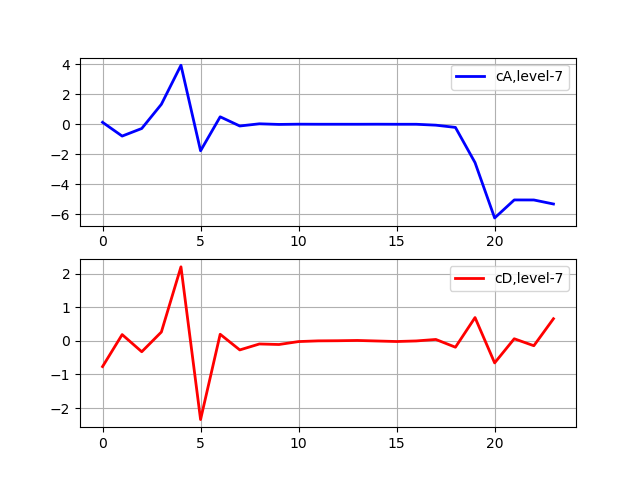
当信号变得短于给定sym5小波的滤波器长度时，分解停止。例如，假设我们有一个频率高达1000 Hz的信号。在第一阶段，我们将信号分为低频和高频部分，即0-500 Hz和500-1000 Hz。在第二阶段，我们将低频部分重新分为两部分：0-250 Hz和250-500 Hz。在第三阶段中，我们将0-250 Hz部分分为0-125 Hz部分和125-250 Hz部分。这一直持续到我们达到最大分解水平为止。

使用FFT傅立叶和小波比例尺分析WAV文件

为了进行分析，请使用WebSDR文件。考虑使用来自scipy.signal的triang的缩减信号分析以及python中离散傅立叶变换的实现（来自scipy.fftpack的fft）。如果序列fft的长度不是2n，则将执行离散傅里叶变换（dft）代替快速傅里叶变换（fft）。这就是这个团队的工作方式。

我们根据以下方案（例如数字数据）使用快速傅立叶变换缓冲区：

fftbuffer = np.zeros（15）; 创建一个填充零的缓冲区；
fftbuffer [：8] = x [7：]; 将信号的末尾移到缓冲区的第一部分； fftbuffer [8：] = x [：7]-我们将信号的开头移到缓冲区的最后一部分； X = fft（fftbuffer）-我们考虑充满信号值的缓冲区的傅立叶变换。

为了使相位频谱更具可读性，可以应用相位部署。为此，使用相位特性的计算来更改该行：pX = np.unwrap（np.angle（X））。

信号片段分析的清单

 import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st='  (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st='    ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st='    ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show()

为了进行比较分析，我们将使用可使用matplotlib中的tree = pywt.wavedec（signal，'coif5'）函数构建的小波比例尺。

列出小波刻度图

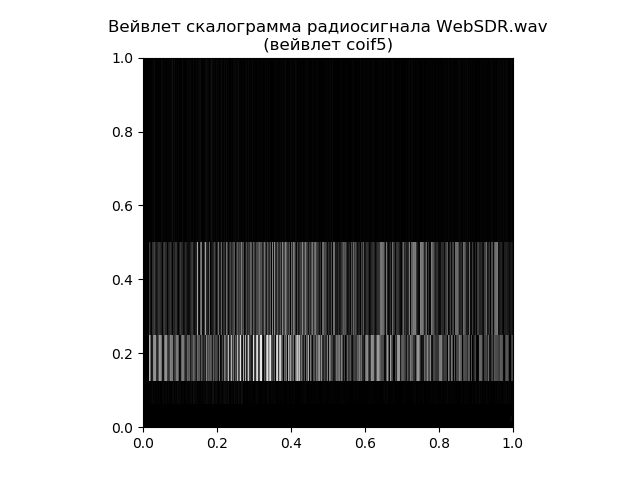
 from pylab import * import pywt import scipy.io.wavfile as wavfile #     ,     . def lepow2(x): return int(2 ** floor(log2(x))) #    MRA. def scalogram(data): bottom = 0 vmin = min(map(lambda x: min(abs(x)), data)) vmax = max(map(lambda x: max(abs(x)), data)) gca().set_autoscale_on(False) for row in range(0, len(data)): scale = 2.0 ** (row - len(data)) imshow( array([abs(data[row])]), interpolation = 'nearest', vmin = vmin, vmax = vmax, extent = [0, 1, bottom, bottom + scale]) bottom += scale #  ,   . rate, signal = wavfile.read('WebSDR.wav') signal = signal[0:lepow2(len(signal))] tree = pywt.wavedec(signal, 'coif5') gray() scalogram(tree) show()

因此，比例图给出了频率随时间的分布问题的更详细答案，而快速傅立叶变换负责频率本身。即使对于这样一个简单的示例，这都取决于任务。

结论

给出了将离散小波变换用于动态信号的原理。
提供了使用PyWavelets 1.0.3（根据MIT许可发行的免费开源软件）进行小波分析的示例。
考虑了实际使用PyWavelets库的软件工具。

小波分析第1部分

引言