解析一个奥林匹克问题，我们将沿着迷宫的产生及其通道蜿蜒曲折的道路走下去，并且还将看到在Julia语言中，算法实现的简单性与其伪代码接壤。

挑战赛

迷宫是一个10×10的方格，在某些单元中有障碍物，而在一个单元中有出口。 机器人处于这样的迷宫中，可以执行4个命令：上下左右移动一个单元格。 如果机器人试图越过迷宫的边界或带着障碍进入笼子，则它会保持在原位。 如果机器人进入出口，则它将退出迷宫，并忽略其他命令。 为机器人编写一个程序，无论机器人在开始时位于哪个单元格，无论如何都要执行该程序到达出口。 该计划不应超过1000个团队。

输入格式

没有条目。 您需要为一个指定的特定条件编写程序
迷宫。
您可以复制的迷宫的版本。 0-空闲单元格，1-障碍物，x-
出路。

0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000 

输出格式

一行由长度不超过1000的字符U，D，R，L组成

准备工作

那些没有使用Julia中的图形的人需要下载软件包

 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #     

在Jupyter中工作最方便，因为图片将在工作期间直接显示。 在这里，您可以找到有关安装的信息，以及针对初学者的介绍和任务。

在我们的任务条件下，有一个迷宫版本可以复制

 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000" 

要绘制迷宫，您需要制作一个矩阵。 由于我们不想手动放置空格，因此我们将使用以下行：

 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] " 

用数字替换笨拙的字母x并解析字符串，我们得到一个定义迷宫的整数矩阵。 然后，为了更大的方便，将“ 1”更改为零，然后将“ 0”更改为1，然后用墙壁将迷宫包围起来：

 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 

在矩阵中

 length(M) 144 

细胞和从他们

 sum(M)-9 70 

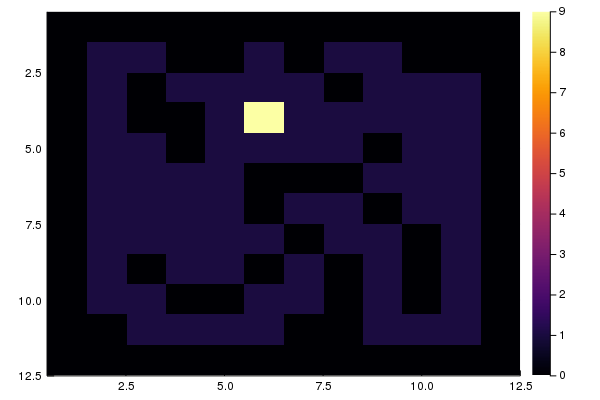
您可以在其上行走的位置-潜在的起始位置。 您可以通过构建二维直方图来显示结果

 using Plots heatmap(M, yaxis = :flip) # flip -   

解决方案验证

首先，您需要制定程序来验证所提出解决方案的正确性。 将复合类型Point设置为使用点和坐标的术语：

 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end 

现在，您需要学习如何将机器人可以理解的一系列命令转换为代码。

这个想法很简单：有一个起点坐标，一条线提出了一种算法，告诉人们如何走路。 我们拿一个字母，看看要踩哪个相邻的单元格。 对于当前坐标，我们添加存储在此单元格中的值。 也就是说，如果零（墙）为零，那么我们将不会移动到任何地方，否则我们将朝所需方向迈出一小步。

利用元编程的功能，您可以用庞大，统一的代码替换输入的方向序列，然后执行它

 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) ) 

但是此方法有许多不便之处，因此，我们将使用经典的条件运算符。 顺便说一下，输出由数字9表示是一个小技巧：为了不检查每个单元格以及是否是出路，我们通过添加存储在特定单元格中的值来启动移动。 当机器人踩到出口时，故意在其坐标上添加一个较大的数字，以使机器人飞越数组的边界，可以使用该块将其捕获为错误：

 try #     catch #       end 

因此，我们实现了一个函数，该函数将c执行字符串str命令来检查机器人是否从点c开始到达出口：

 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end 

让我们收集一个将迭代所有起始位置的函数

 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

检查命令：

 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false) 

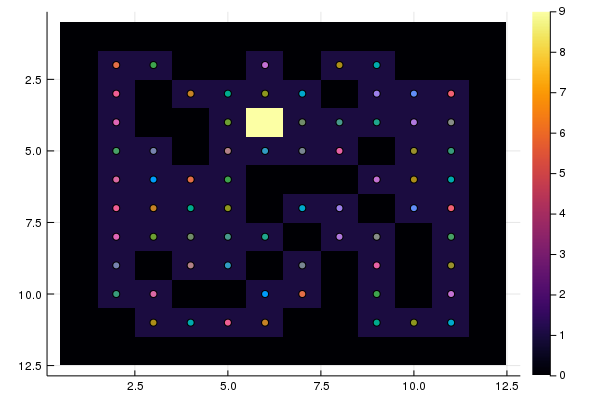
所有出发点均经过测试，只有10个导致退出。 必须建立从每个点到出口的路线。

在探究迷宫的产生和传播之前，我们将保存我们的结果。 我们将使用Images.jl包，该包在图像处理领域提供了许多可能性（一个很好的例子 ）。 他的支持工具之一是Colors.jl软件包， 它扩展了Julia的颜色处理能力。

 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze) 

深度搜寻

从关于哈勃（Habr）的文章中实现了这个想法。
这个想法很简单：创建墙壁网格

 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl 

然后，通过循环，我们突破了路线和分支。 我们定义了一个函数，该函数查找相邻的未访问区域（例如，将它们用平局指定），并返回这些相邻项之一（如果没有未访问的相邻项，则返回标记点）：

 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end 

我们将像这样打破墙壁：

 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end 

演算法

1. 使初始电池成为当前电池并将其标记为已访问。
2. 虽然有未访问的单元格
   1.如果当前单元格未访问“邻居”
   1.将当前单元格推入堆栈
   2.从附近选择一个随机单元格
   3.移除当前单元格和选定单元格之间的墙
   4.使选定的单元格为当前单元，并将其标记为已访问。
   2.否则，如果堆栈不为空
   1.将笼子从堆栈中拉出
   2.使其最新
   3.否则
   1.选择一个随机未访问的单元，使其成为当前单元并将其标记为已访问。

 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt) 

回溯路径搜索算法：

1. 使初始电池成为当前电池并将其标记为已访问。
2. 直到找到解决方案
   1.如果当前单元格未访问“邻居”
   1.将当前单元格推入堆栈
   2.从附近选择一个随机单元格
   3.使所选单元格成为当前单元格并将其标记为已访问。
   2.否则，如果堆栈不为空
   1.将笼子从堆栈中拉出
   2.使其最新
   3.否则，没有出路。

相反，我们正在一个小区的半径内而不是通过一个小区来寻找邻居：

 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end 

定义通过绘制路线和失败尝试通过迷宫的算法

 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end 

正如某些人所注意到的，也调用了一个函数，就像算法生成的函数一样（多重调度）。 当您用两个数字调用它时，它将解决构造迷宫的方法，但是如果您通过指定图像和两个点（输入和输出的坐标）作为参数来调用它，则在输出处我们会得到一个传递了迷宫的图像

 img0 = load("D:/dat/maze111.png") amazeng(img0) 

让我们尝试一下我们的迷宫：

 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) ) 

即使您修改功能以记住路线，该算法仍然会因为空白而被证明是无效的。 但是迷宫出来的很棒。

Prim的随机算法

一旦开始绘制迷宫，您就不会停止。 让我们执行另一个有趣的算法 ：

• 从充满墙壁的网格开始。
• 选择一个单元格，将其标记为迷宫的一部分。 将单元格墙添加到墙列表。
• 虽然列表中有墙：
  
  • 从列表中选择随机墙。 如果仅访问墙共享的两个单元之一，则：
    
    • 使墙壁成为通道，并将未访问的单元标记为迷宫的一部分。
    • 将相邻的单元格墙添加到墙列表。
  • 从列表中删除墙。

 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze) 

事实证明，它更具分支性，并且同样出色，尤其是在组装过程中。

现在，我们实现了用于查找最短路径的最通用算法：

方法A *

• 创建了2个顶点列表-待处理且已审阅。 将起点添加到待处理的起点，到目前为止，已审核的列表为空。
• 为每个点计算 $$$H$-从点到目标的大概距离。
• 从要考虑的点列表中，最小的点 $$$H$。 让她 $$$X$。
• 如果 $$$X$-目标，然后我们找到了路线。
• 我们随身携带 $$$X$从待处理列表到已审核列表。
• 对于相邻的每个点 $$$X$（表示该相邻点 $$$Y$），请执行以下操作：
  
  • 如果 $$$Y$已经在评论中-跳过它。
  • 如果 $$$Y$尚未在候补名单上-在此添加。
• 如果要考虑的点列表为空，但我们尚未达到目标，则该路线不存在。

首先，让我们定义“点”类，它将知道它与目标有多远：

 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end 

现在，我们为结构定义一个比较操作，一种用于确定数组中元素存在的方法，以及删除元素，查找点之间的距离并列出邻居的功能：

 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right 

与往常一样，可以使用以下命令来澄清晦涩的运算符： 例如?splice ?argmin 。

而且，实际上，方法A *本身

 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end 

我们将迷宫图像加载到图片中并以矩阵形式呈现：

 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0)) 

我们建立了一条从任意点退出的路线：

 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M) 

来自所有位置的搜索如下所示：

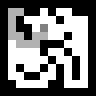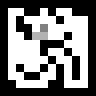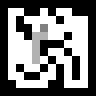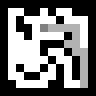
看到代理 冲 总是趋向出口，经常变成死胡同，这会导致不必要的步骤，并且会记住整个路线。 通过A *算法稍微复杂一点的版本可以避免这种情况。

• 创建了2个顶点列表-待处理且已审阅。 将起点添加到待处理的起点，到目前为止，已审核的列表为空。
• 为每个点计算 $$$F = G + H$。 $$$G$-从起点到终点的距离， $$$H$-从点到目标的大概距离。 每个点还存储指向其起点的链接。
• 从要考虑的点列表中，最小的点 $$$F$。 让她 $$$X$。
• 如果 $$$X$-目标，然后我们找到了路线。
• 我们随身携带 $$$X$从待处理列表到已审核列表。
• 对于相邻的每个点 $$$X$（表示该相邻点 $$$Y$），请执行以下操作：
  
  • 如果 $$$Y$已经在评论中-跳过它。
  • 如果 $$$Y$尚未在等待列表中-在此处添加它，记住指向的链接 $$$X$并且已经计算 $$$Y.G$（这是 $$$X.G$+距 $$$X$之前 $$$Y$）和 $$$Y.H$。
  • 如果 $$$Y$在列表中以供考虑-检查是否 $$$X.G$+距 $$$X$之前 $$$Y$$$$<Y$所以我们到了重点 $$$Y$较短的方法，更换 $$$Y.G$在 $$$X.G$+距 $$$X$之前 $$$Y$以及他们的出发点 $$$Y$在 $$$X$。
• 如果要考虑的点列表为空，但我们尚未达到目标，则该路线不存在。

但是，即使有不必要的步骤，我们的选择也完全在任务的限制之内，因此修改程序将是您的功课。

直到奥运会结束，我们什么都没剩下，但是我们仍然需要学习如何将算法的结果转换为"RRLUUDL..."形式的命令。

在经历了所有这些迷宫之后，我们可以假定解决方案要简单得多。 实际上，一个简单的选择马上就产生了，但是我真的很想制造精美的东西 。

如果我们将我们的艺术家放在一个空旷的地方并开始随机散步，他会在出发位置附近犹豫。 但是随着墙的引入，部分方向将开始消失，自由度将变小，并且在输入数据相同的情况下，主体将移动更大的距离。

这是我们的团队检查版本，以适合从迷宫中解救机器人：

 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end 

现在，生成随机行就足够了，直到您获得了一个适用于所有起始位置的行：

 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70 

另外，有可能不用担心测试。 读取任务并生成具有最大允许条件的随机字符串就足够了：

 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70 

也就是说，生产线将通过测试的可能性为70％。

仅此而已。 我希望读者能够成功的随机，耐心和直觉，寻求明显的解决方案。

对于好奇者-可以加深主题的链接：

• 迷宫时代最完整的游览
• 俄语版
• 时代方法
• 两种方法
• 埃勒算法
• 在线发电机
• 在线查找点之间路径的方法
• 跳点搜索路径算法
• 维基百科上的*
• A *简介
• 算法A简介*
• 路径查找算法的说明
• 艺术来源