本文的撰写提示了此评论 。 更准确地说，就是其中的一句话。

...花费数十亿美元的内存或处理器周期是不好的...

碰巧的是最近我不得不这样做。 而且，尽管我在本文中考虑的情况非常特殊-结论和适用的解决方案可能对某人有用。

一点背景

iFunny应用程序处理大量的图形和视频内容，并且模糊搜索重复项是非常重要的任务之一。 这本身就是一个重要的话题，值得单独撰写，但今天，我将只讨论一些与此搜索有关的计算非常大的数字数组的方法。 当然，每个人对“非常大的阵列”都有不同的理解，与强子对撞机竞争是愚蠢的，但仍然如此。 :)

如果算法很短，则对于每个图像，它的数字签名（签名）是由968个整数创建的，并且通过查找两个签名之间的“距离”来进行比较。 考虑到仅过去两个月的内容量就达到了约1000万张图像，那么细心的读者就会轻易地想到它-这些恰恰是“数十亿个元素中的元素”。 谁在乎-欢迎猫。

开头会有一个枯燥乏味的故事，关于节省时间和内存，结尾处有一个简短的说明性故事，即有时查看源代码非常有用。 引起关注的图片与该说明性故事直接相关。

我必须承认我有点狡猾。 在对该算法的初步分析中，可以将每个签名中的值数量从968减少到420。它已经是原来的两倍，但是数量级保持不变。

虽然，如果您考虑一下，这并不是我所欺骗的，这将是第一个结论：在继续执行此任务之前，值得考虑一下-是否可以通过某种方式预先简化它？

比较算法非常简单：计算两个签名差异的平方和的根，然后除以先前计算的值的总和（即在每次迭代中，总和仍将是并且不能完全取为常数）并与阈值进行比较。 值得注意的是，签名元素被限制为-2到+2的值，因此，差的绝对值被限制为0到4的值。


没什么复杂的，但数量决定。

天真的第一方法

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

让我们计算一下这里的操作数：

10M平方根Math.sqrt
10M增加和划分/ (first.norma + second.norma)
4.200M减法和平方Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M添加.sum()

我们有哪些选择：

1. 有了这样的卷，花费整个Byte （或者，天哪，有人会猜想使用Int ）来存储三个有效位是不可原谅的浪费。
2. 也许，如何减少数学量？
3. 但是是否可以进行一些初步的过滤，而这在计算上并不那么昂贵？

第二种方法，我们打包

顺便说一句，如果有人建议您如何使用这种包装简化计算，您将得到极大的感谢，并加深因果报应。 虽然一个，但我全心全意:)

一个Long是64位，在我们的情况下，它将允许我们在其中存储21个值（而1位将保持未结算状态）。

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

从内存上来说更好（ 4.200M与1.600M字节），但是计算呢？

我认为很明显，操作数量保持不变，并且8.400M班次和8.400M逻辑8.400M ，也许可以对其进行优化，但是趋势仍然不8.400M -这不是我们想要的。

第三种方法，用子潜艇重新包装

早上我可以闻到它的气味，在这里您可以使用魔法！

让我们以三个位而不是三个值来存储值。 通过这种方式：

是的，与以前的版本相比，我们将丢失堆积密度，但是我们将有机会一次用一个XOR接收16个（不太完全）差异的Long 。 另外，每个最终半字节中的位分配只有11个选项，这使您可以使用平方差的预先计算值。

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

从内存来看，它变成了2.160M而1.600M ，但仍然比最初的4.200M 。

让我们计算一下操作：

10M万平方根，加法和除法（无处不在）
270M XOR的
4.320从数组中进行加法，移位，逻辑4.320以及提取。

它看起来已经很有趣了，但是无论如何，计算量太多了。 不幸的是，似乎我们已经花费了这20％的努力来提供80％的结果，是时候考虑您还能从中获利的时候了。 首先想到的是根本不进行计算，而是使用一些轻量级的过滤器过滤掉明显不合适的签名。

第四种方法，大筛

如果稍微转换计算公式，则会得到以下不等式（计算的距离越小越好）：


即 现在，我们需要根据在Long设置的位数获得的信息，找出如何计算不等式左侧的最小可能值。 然后，简单地丢弃所有不满足他要求的签名。
让我提醒您，x _i可以取0到4之间的值（该符号并不重要，我认为很清楚为什么）。 假定每个项都是平方的，则很容易得出一个通用模式：


最终公式如下所示（我们将不需要它，但我推论了很长时间，只是忘记而不向任何人展示是可耻的）：


其中B是设置的位数。

实际上，仅用一个Long的64位读取64个可能的结果。 并与上一节类似，可以对它们进行预先完美的计算并添加到数组中。

此外，计算所有27个Long完全是可选的-足以超过下一个阈值，您可以中断检查并返回false。 顺便说一下，可以在主要计算中使用相同的方法。

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

在此必须理解，该滤波器的有效性（最高为负）灾难性地取决于所选的阈值，而强度略微小于输入数据。 幸运的是，对于所需的阈值d=0.3相当少量的对象成功通过了过滤器，并且它们的计算对总响应时间的贡献微乎其微，以至于可以忽略不计。 如果是这样，那么您可以节省更多。

第五种方法，摆脱顺序

在处理大型集合时， sequence可以很好地防御极其令人不快的内存不足 。 但是，如果我们显然知道在第一个过滤器上将集合缩减为合理的大小，那么一个更合理的选择是在创建中间集合的循环中使用普通迭代，因为sequence不仅时髦又年轻，而且是迭代器，其中有远非免费的hasNext同伴。

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

看来这里就是幸福，但我想“让它变得美丽”。 在这里，我们来谈谈承诺的教学故事。

第六种方法，我们想要最好的

我们在Kotlin上编写，这里有一些外国java.lang.Long.bitCount ！ 最近，无符号类型被引入该语言。 进攻！

言归正传。 所有ULong均由ULong代替， ULong从Java源代码中ULong并重写为ULong的扩展函数

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

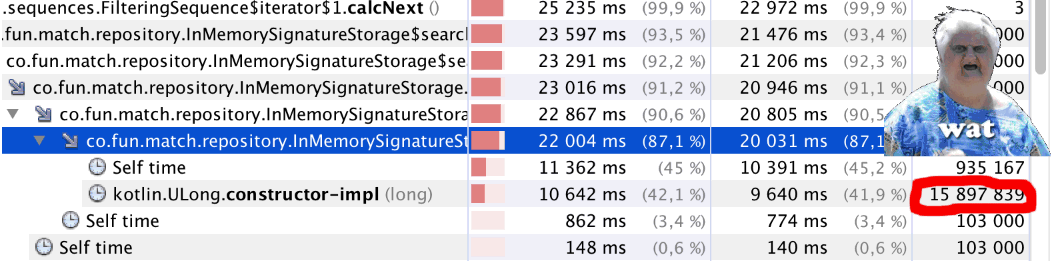
我们开始，……出了点问题。 代码开始工作的速度明显变慢。 我们启动了探查器，并看到了一些奇怪的东西（请参阅文章的bitCount() ）：对bitCount()调用少于一百万次， bitCount()对Kotlin.ULong.constructor-impl调用几乎为Kotlin.ULong.constructor-impl百万。 WAT！？

谜语的解释很简单-仅查看类代码ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

不，我了解一切， ULong现在ULong experimental ，但是那是怎么回事！
总的来说，我们认为这种方法是失败的，这很遗憾。

好吧，但是，也许还有其他可以改进的地方吗？

其实可以。 原始的java.lang.Long.bitCount代码不是最佳的。 在一般情况下，它可以提供良好的结果，但是如果我们事先知道我们的应用程序可以在哪些处理器上运行，那么我们可以选择一种更好的方法-这是有关Habré的一篇非常不错的文章。

我使用了“组合方法”

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

数鹦鹉

所有测量都是在本地计算机上进行开发时偶然进行的，并从内存中复制出来，因此很难说出任何精度，但是您可以估算出每种方法的大致贡献。

结论

• 在处理大量数据时，值得花时间进行初步分析。 也许并非所有这些数据都需要处理。
• 如果您可以使用粗略但便宜的预过滤功能，则将大有帮助。
• 一点魔术就是我们的一切。 好吧，当然适用。
• 查看标准类和函数的源代码有时非常有用。

感谢您的关注！ :)

是的，将继续。