免费的入门课程是Skyeng School功能。 潜在的学生可以熟悉平台上的语言,检查他的英语水平,最后,请尽情玩乐。 对于学校而言,入门课程是销售渠道的一部分,然后是第一笔付款。 这是由入门课程方法学家进行的,这是一个由老师和销售人员组成的特殊人员,无论客户是否购买了第一包产品,以及他是否完全上课,他的时间都是有偿的。 旷课是非常普遍的情况,因此,教训的代价太高了。
在本文中,我们将介绍如何借助分析模型和航空公司的经验将入门课程的成本降低近一半。
Skyeng销售漏斗包含五个步骤:在站点上注册,通过销售入门入门课程,入门课程,调用第一销售线,打响第二销售线,支付第一包费用。 早些时候,在第一个电话之后,我们为当时正在等待学生的特定入门课程方法学家设置了课程时间。 如果一个人签了名却没有来,则方法学家会浪费他的时间和学费-这段时间要花钱。 缺勤的平均发生率是一半。 入门课程后,三分之一的客户购买了第一包产品。 因此,从录制到入门课程到支付的转换仅为0.15。 在旧方案中,成功的入门课程(转换为付款)花费了我们4,000卢布,而我们必须为此做些事情。
您可以简单地拒绝它,但是在这种情况下,最终从铅到付款的转换将大大减少,这不适合我们。 我们将不得不寻找另一种解决方案,构建模型,进行计数和实验。
第一煎饼
我们转向了航空公司的经验,特别是超量预订的做法。 航空公司知道,购买机票的乘客中有100%很少乘坐飞机,因此可以通过卖出比飞机座位多的机票来利用这一优势。 如果突然有所有乘客降落,您会发现其中的志愿者准备起飞,准备下一次飞行的下一个面包。 航空公司因此增加了利润,我们可以通过类似的方法降低成本。
因此:我们拒绝将记录发送给特定的人,我们创建了一个入门课程的方法论者库,我们期望他们中的应用不会出现,从而分散了他们之间的应用。 如果还有更多建议,我们建议您注册另一天。 我们在测试中启动了这样的MVP,立即意识到我们做错了所有事情。
参加入门课程的学生中有一半是统计人员,实际上,该比例根据该人来自的时间,日期,渠道的不同而有很大差异。 此外,超过80%的潜在学生,由于对推迟课程的建议而立即退学,或者没有获得第二名。 所有这些都可能导致这样的事实,在糟糕的日子里,我们将失去多达三分之一的客户。 测试已关闭,并以一种智能的方式进行了所有操作。
模型,预测,多项式
首先,有必要找出参加入门课程的人的比例。 第一个观察结果是,这取决于人来自何处的营销渠道。 从转换到付款的角度,我们将这些渠道划分为“热”和“冷”,“热”表示较高的转换,“冷”表示较低的转换。 事实证明,“通道温度”以几乎相同的方式影响到入门课程输出的转换。
继续进行航空类比,我们为来自不同渠道的潜在客户制作了不同的“值机台”,将它们的系数与该渠道出现的历史概率相对应:0.8、0.4和0.2。 对于“热门”渠道,我们分配了更多的“冷”的方法专家-更少。 这种方法效果更好,但是在糟糕的日子里,仍有超过20%的“出发”(参加免费入门课程的客户多于免费的方法论者)。 他们试图通过增加0.1的余量来增加系数:一方面,我们越是聘用方法论者,就越不会失去客户;另一方面,开展入门课程的成本也在不断增加。
从这些观察,第二个MVP增长了。 对于每个已注册的学生,我们都会对他参加入门课程的可能性进行预测。 我们进行联合概率分布和置信区间,置信度为95%。 在少数情况下,如果有更多的客户涌出来而不是计划的话,我们会保留一个方法学家储备库-当前正在从事非紧急工作(例如检查论文)的老师。
为了计算特定学生的预测,我们基于历史数据并考虑了以下几个因素,建立了一个统计模型:渠道,地区,儿童/成人,私人/公司客户,从录制到入门课程的时间。
该模型具有以下概念:
- slot :入门课程的日期和时间;
- 校正因子 :在这一天和这一小时异常退出的可能性;
- 应用权重 :给定客户退出的允许概率;
- 出发 :未提供服务的应用程序(客户端已退出,所有方法学家都很忙);
- 简单的方法论者 :结果少于预期,人们无所事事;
- 限制 :置信区间的%,此后模型将禁止向该广告位添加订单。
每个插槽包含N名方法学家,并且插槽本身具有校正因子 k(以100为底)。 可用于该模型的方法学家的数量定义为舍入(N * k / 100)。 当出现一个应用程序时,模型将确定其权重 ,查看插槽中已有的此类权重之和,如果由于添加此应用程序而导致插槽中的应用程序权重之和不超过方法专家的人数,则确定该插槽是否可用。 评估模型的度量标准是:离场比例(必须最小化),广告位负载(最大化),客户的入门课程等待时间(最小化)。 可变的模型参数包括应用程序权重和限制 。
为了预测将释放多少客户,使用了概率乘积的公式:

考虑到所有可能的输出组合,我们得到的自然概率分布非常接近。 一百个客户的分配如下所示:

应用置信区间,我们可以调整模型的积极性。 例如,将限制向左移动会增加限制,即 我们用相同数量的方法学家释放了更多的客户,而向右移动会减少这种情况,因为 限制提前触发。 限制为90%和57%的示例:
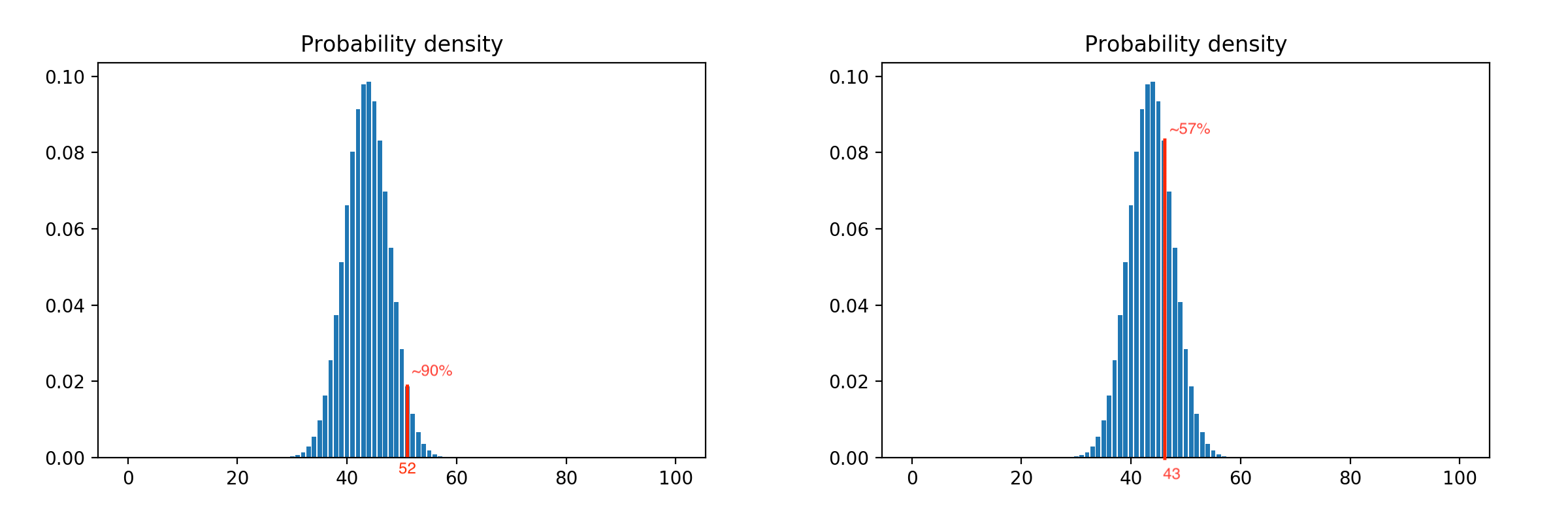
此外,可以通过校正因子来调整模型的主动性:减少会降低模型,增加会提高模型。 当我们知道在特定的一天/小时,某些外部因素会导致异常时,这很有用。
概率相乘的公式在测试中表现良好,但是从计算角度来看很困难,因此我们用多项式重写它:

该模型的缺点包括:
- 由于它基于历史数据,因此对出口的突然变化没有很好的响应;
- 如果方法专家发生不可抗力事件并且他退出了比赛,这几乎是可以保证的离职,则管理人员需要紧急重新分配课程;
- 如果渠道“热”的动态标记下降,则该模型将错误地估算出客户出现的可能性。
使用此模型的结果是,我们在入门课程中节省了多达45%的成本,对客户的损失最小。
为什么不使用机器学习?
由于统计模型运行良好,并且与其使用ML提高现有预测的准确性相比,将ML开发人员的工作引向其他任务更有利可图。
例如,我们正在为潜在客户开发一个评分系统,该系统与银行客户非常相似。 银行使用评分来确定还款的可能性,我们可以确定首次还款的可能性。 如果费用很低,则无需花费资源来组织入门课程; 相反,如果价格很高,则可以立即将客户发送到付款页面。
但是,这个故事还有一段时间了。