为了将消息从基站传输到移动设备(反之亦然),电磁波必须克服许多障碍:反射,折射,散射,阴影,多普勒频移等。 首先,根据这些影响的数学模型,将所有这些影响称为乘性(英文。乘法-乘法)。 其次,它可以在衰落的一般术语下收集。
从标准到标准,从一代到一代,从技术到技术,科学家和工程师都在努力解决这些衰落的问题(缓解衰落)。
并且一些解决方案很普遍。 让我们多说一点:几乎所有的一种或另一种方式都与多样性的概念有关。

插图的来源 (不,这不是广告,只是所需术语和猫的成功组合)。
此类解决方案的示例:
- 跳频 -防止频率选择性衰落;
- 通过反馈进行信道估计和均衡-GSM,以抑制时域变化;
- 频谱扩展 (UMTS);
- 下行链路(下行链路)上的导频信号(从UMTS开始)和上行链路(上行链路)上的信号跟踪(信号跟踪)–抑制时域变化;
- OFDM -LTE,防止频率选择性衰落;
- 时间分集( 纠错编码 );
- 极化分集(在发射机侧)+加法器(在接收机侧的组合器);
- 空间多样性 。
我们今天将考虑这些技术中的最后一个,作为MIMO另一个主题的一部分。
空间分集阶数和阵列增益
第一个。
有这样一个概念-空间分集顺序:如果可以从不同方向收集相同的信息 ,则恢复该信息的希望将会正确地增加。 作为生活中的一个例子,我们可以想象从独立的信息提供者那里收集有关同一事件的信息。 在无线电通信中,我们可以增加此顺序,包括使用MISO , SIMO或MIMO 。
这种多样性的理论极限  在哪里
在哪里  -发射天线的数量,以及
-发射天线的数量,以及  -接收天线的数量。 记住这一点。
-接收天线的数量。 记住这一点。
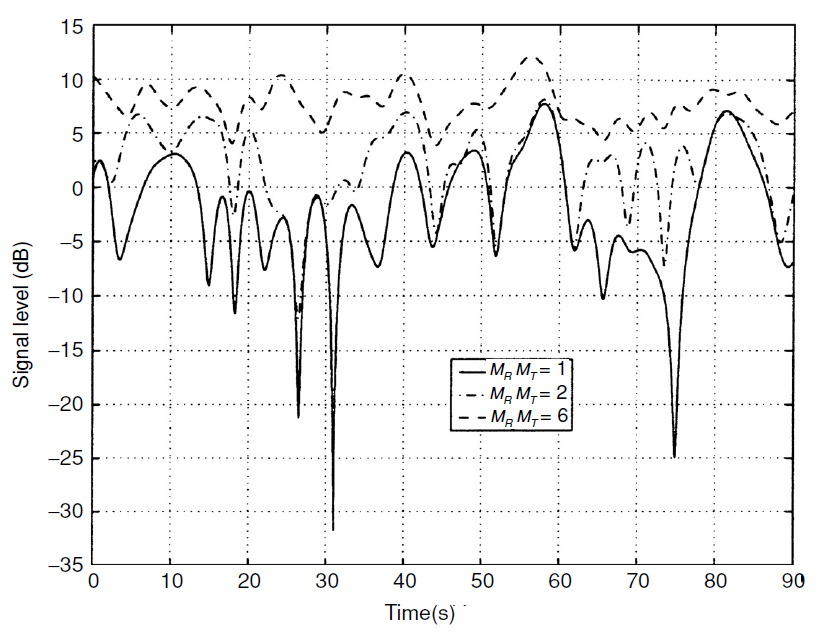
图1。 空间分集阶数增加导致信道稳定性。 在值  信道已完全稳定,将变为无衰落信道(AWGN)[1,第101页] 。
信道已完全稳定,将变为无衰落信道(AWGN)[1,第101页] 。
第二个。
使用SIMO , MIMO甚至MISO (在知名信道的情况下),人们可以获得所谓的阵列增益 。 这意味着使用多个接收天线和/或在发送端进行适当的能量分配可以提高信噪比(SNR)-从而减少错误数量。
可以通过分析得出各种配置的分集和阵列增益的阶数[1,p。2]。 86-100]并缩小到一张桌子[1,p。 [101]既针对信道未知的情况(CU-信道未知),又针对发射机侧信道已知(CK-信道未知)的情况。
好的,即使是较宽的笔触,但现在我们至少对抑制衰落的理论方面有了一定的了解。 下一个问题是如何达到这些理论极限? 激活考虑的奖金有哪些技术?
解决方案编号1。 时空码
对于空间分集,最流行的解决方案类别之一是空时代码(时空代码)。 例如,我认为,许多Alamouti方法(块码示例)[2,p。 40-46]:
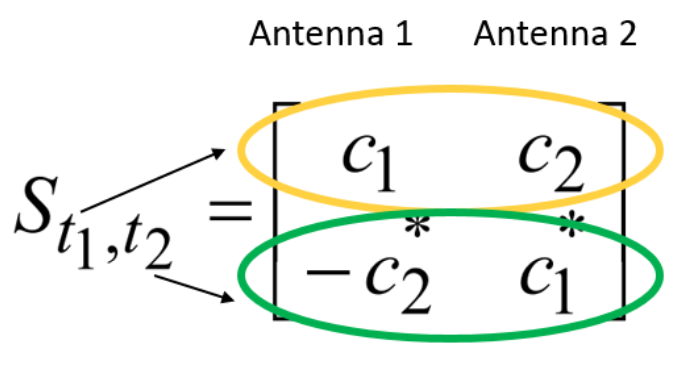
在哪里  在
在  是一些输入字符
是一些输入字符  在
在  是时隙,并且
是时隙,并且  -实际上,这是一个编码矩阵。
-实际上,这是一个编码矩阵。
Alamouti方案是正交的 [1,pp。93-95,97-98],最重要的是, 它不需要信道状态信息。
在我的存储库中,可以找到关于由Alamouti方案编码的信号的传输的数学描述,以及在MatLab中对该技术进行建模的几个示例。 有兴趣的欢迎!
但是,如您所见,在Alamouti电路中,我们只有两个发射天线(  )
)
但是请不要灰心:当然,还有其他选择,它们的名称略有不同。 例如,根据[3],可以应用以下编码方案:
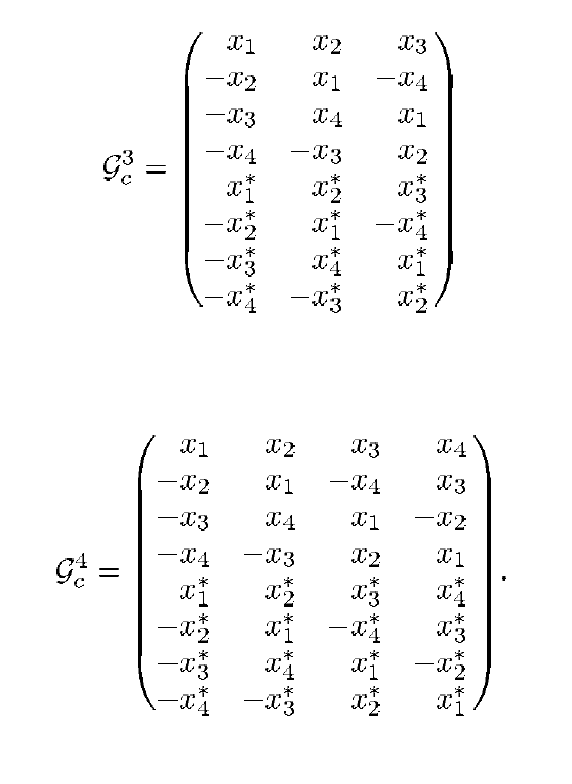
图 2.案件转移方案  和
和  [2]。
[2]。
还有许多其他选择:仅满足正交条件。
实际上,这样的代码需要与Alamouti代码相同的编码和解码过程。 因此,它们通常在通用术语正交空时分组码 (OSTBC-正交空时分组码)下组合。
MathWorks的“ MIMO系统简介”资料中对此类代码给予了极大的关注。 我强烈建议每个有兴趣的人阅读它!
价格多少?
从传输方案可以看出,尽管我们并行传输符号,但是我们在此花费了几个时隙。 因此,我们牺牲带宽(至少得到的带宽更少)。 对于Alamouti方案,这种折衷是对称的:我们使用2根天线和2个时隙(就带宽而言好像使用SISO)。 其他方案可能会进一步影响传输速度。
决定号2。 DET:主要本征模式传输
好吧,对于上一类技术,渠道的知识对我们而言并不重要。 但是,如果我们仍然掌握这些知识怎么办? 在这种情况下,还有其他合适的技术吗?
在我以前的一篇文章中,我们讨论了在了解现有信道状态的情况下,我们可以应用各种信号处理方法来提高吞吐量。 相同的原理可以提高抗扰度。
可能有很多人听说过MRC方法,并且很多人知道这种方法非常适合SIMO情况,即传输中至少有一根天线,但仍然很多,这意味着需要组合一些东西。
但是,可能已经有较少数量的阅读器在发送端(Tx-MRC)遇到了MRC [1,p。 95.96],甚至使用DET技术(主导本征模式传输)的情况更少[1,p。95.96]。 98-100]。 修复它!
首先,请考虑MIMO信道的一般情况以及这些方法中的最后一种-DET。
的本质是什么:
- 如果发射器有矩阵
 然后就可以处理了。
然后就可以处理了。 - 例如,通过SVD分解它:
 从而获得具有某种性质的几个矩阵
从而获得具有某种性质的几个矩阵 - 这些属性可用于优化传输,例如通过使用预编码。
我们介绍一些预编码向量:
在哪里  是第一个(可以说是主要的)矩阵向量
是第一个(可以说是主要的)矩阵向量  。
。
此外,我们还可以编写后处理矢量:
在哪里  是矩阵的第一个向量
是矩阵的第一个向量  。
。
重新定义接收信号的模型(请参见带宽主题 ):
瞧! 线性代数的魔力在所有分配路径中脱颖而出,并在此分配所有能量。 实际上,我们前面有一个线性波束成形算法。
与OSTBC一样,这种方法的代价是带宽限制。 没错,这现在纯粹是在空间领域发生的。
如果我们只讲奇异值,为什么该方法的名称中包含特征值?因为特征值(传播路径的基数—衰落)可以直接从奇数(衰落幅度)得出:
好吧,有了DET,或多或少就清楚了Tx-MRC是什么?
和他在一起更容易-这是DET的特例,现在我们将证明这一点。
对于Tx-MRC,文献中提出了以下预编码向量:
我们牢记Frobenius范数的平方等于特征值,因此等于奇数的平方  (对于SIMO和MISO)。
(对于SIMO和MISO)。
然后,仅在MISO情况下,我们再次重新定义接收信号的模型:
需要证明。
注意,现在我们不仅在谈论发送侧的信号分离,而且在接收侧将它们组合起来,就像OSTBC一样。 现在我们在谈论能量的最佳分配。 这意味着在这种情况下, 阵列增益的值高于OSTBC的值。
现在已经讲完所有单词,我们将尝试模拟我们的技术。
造型
今天我数了一下:对于OSTBC建模,使用了来自Communication Toolbox的现成对象(MatLab R2014a-是哪个):
对于调制和解调(以及误码计算-BER),不再使用功能 ,而是使用功能 。 它们的类似物位于通信 Octave软件包中。
源代码可以在这里找到。clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2;
结果应该是这样的:
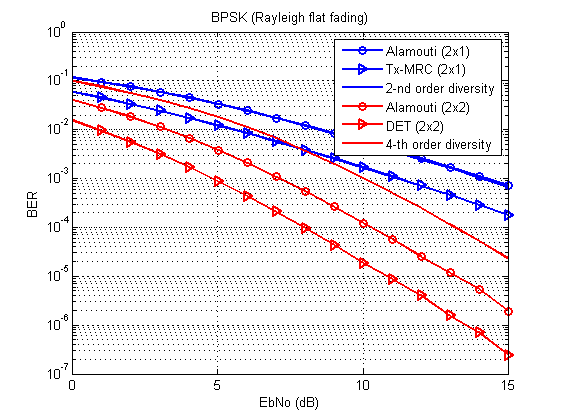
图 3.不同传输技术(BPSK,平坦衰落的瑞利信道)的位/符号误差曲线。 与[1,p。 96,100]。
现在的问题是:二阶分集的理论边界的曲线在哪里?
答案一切都按照表格进行:该曲线与Alamouti 2x1完全重合。 在MIMO的情况下,阵列增益也起作用,因此曲线是分开的。
无论哪种方式,DET(或Tx-MRC)的质量都有望超过Alamouti。
像这样:知识就是力量!
文学作品
Paulraj,Arogyaswami,Rohit Nabar和Dhananjay Gore。 时空无线通信简介。 剑桥大学出版社,2003年。
Bakulin M.G.,Varukina L.A.,Kreindelin V. B. MIMO技术:原理和算法// M .:热线–电信。 -2014年。-T. 244。
Tarokh,V.,Jafarkhani,H.和Calderbank,AR(1999)。 正交设计的时空分组码。 IEEE Transactions on Information theory,45(5),1456-1467。
聚苯乙烯
在我的母语专业的老师和学生友爱中,我问好!