众所周知,研究人员必须处理的大多数时间序列都是非平稳的,并且其分析要比固定过程的研究复杂得多。 由于对小波的兴趣似乎已消退,因此讨论一些其他“非平稳”仪器非常有用,这些仪器主要用于估计瞬时频率以及评估瞬时频谱。
首先,召回“分析信号”是有意义的。 下文中,“ An模型”是指测试信号的虚部完成后(相位偏移π/ 2)的瞬时阻抗和功率。
但是,并非总是可以修补吉尔伯特的转变。 之前,已经
提到了适用于短序列的自回归谱估计方法。 在这里,“ AR模型”将被理解为对原始信号的短(5个样本)重叠片段的研究,以便确定二阶自回归系数,从中找到模型的“极点”等。
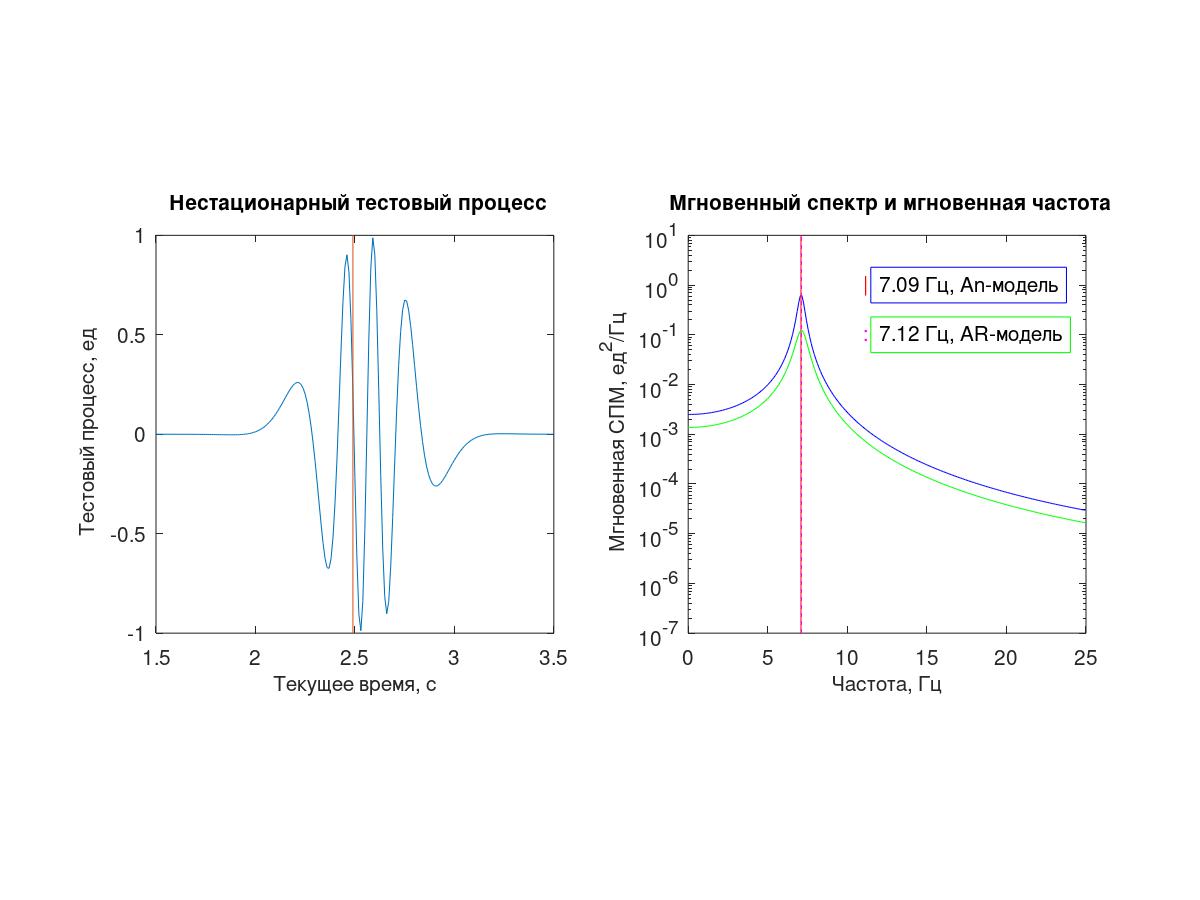

这里描述的两种方法都基于一个原理-假设在选定时刻的一小部分中,所研究的过程可以通过“指数”序列近似-一个复数(An)或两个复数共轭指数(AR)的总和。
作为测试过程,使用了从连续确定性过程(1)获得的512个条件采样间隔Δt= 0.01 s的样本序列。
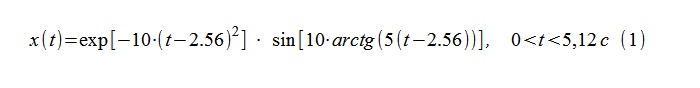
通过“对数”以及随后分别从(1)到高频填充和包络的微分,可以获得(瞬时)频率和减量的理论表达式(2)

对于通过周期图方法(直接和傅立叶逆变换)进行An建模,从初始序列x [i]生成分析信号y [i]。
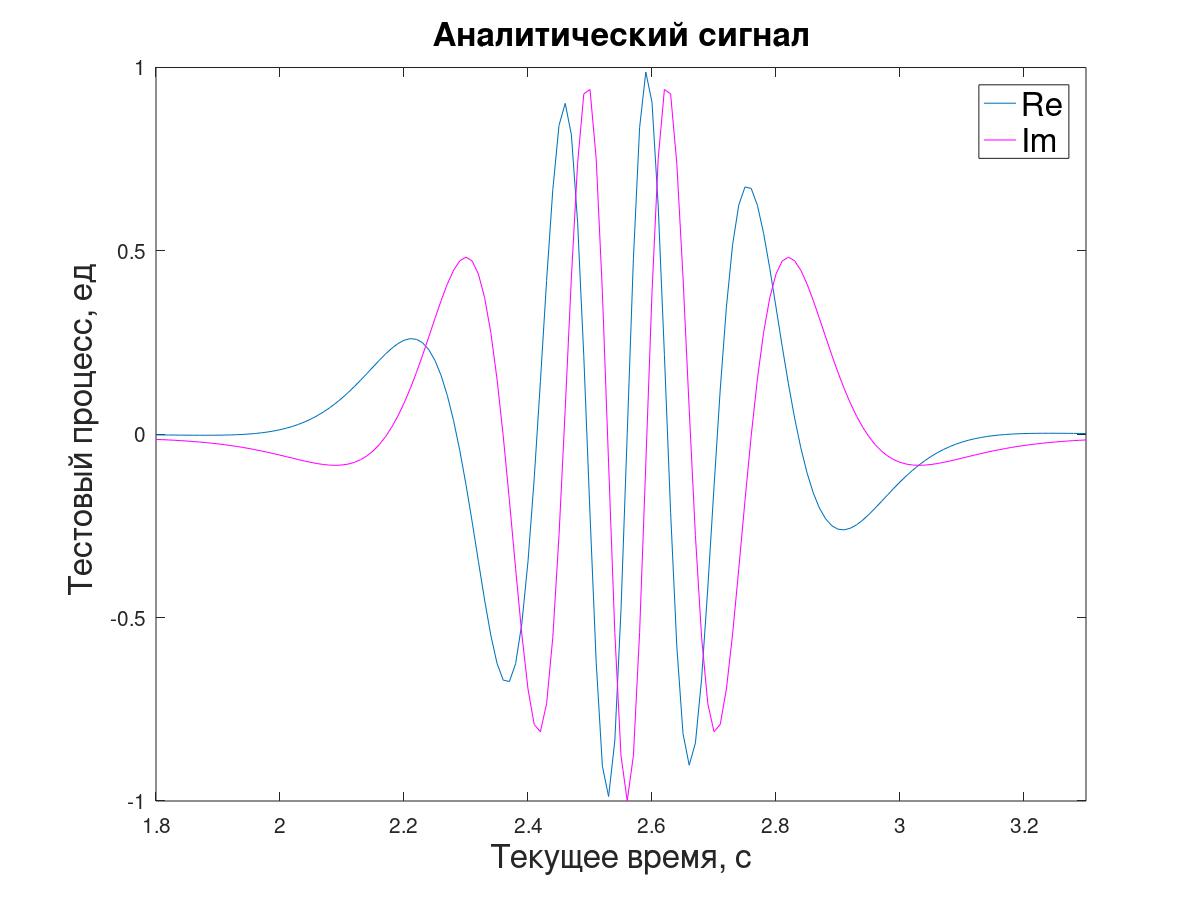
原则上,这样一个信号的两个连续采样的比率可以让您确定瞬时阻抗λ,但是为了简化此演示任务-为了不打扰创建中间采样或解释估计值Δt/ 2的偏移,我们决定使用“通过一个”的采样来计算λ
i相对于先前y [i-1]的后续y [i +1]信号值(3)。

对于AR建模(二阶模型),使用了使用Yule-Walker方程计算自相关系数1,a
1i ,a
2i的标准程序,以及5个样本序列x [i-2],x [i -1],... x [i + 2](4)。
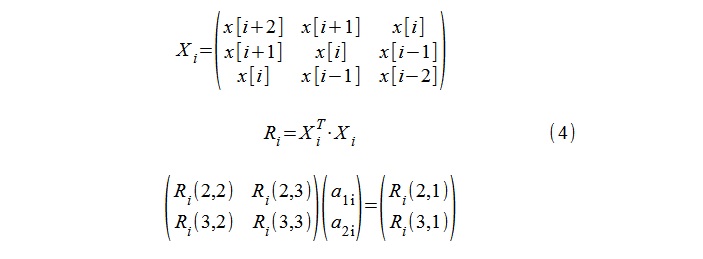
然后,可以通过二次方程式(5)的根的对数轻松计算模型λi的“极点”。
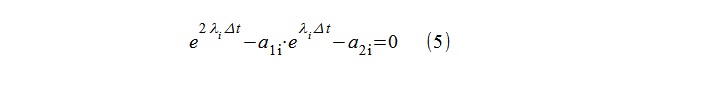

从已知“极点”到比例因子的频谱估计的构建
并不困难 。 下一个 An模型的“瞬时功率”显然定义为| y [i] |
2 ,缩放此估计的问题似乎已经解决。 对于AR模型,在信号不稳定的情况下,与确定常规白噪声功率有关的常用技术“不起作用”。 由于缺乏最好的主意,因此根据相应的5个样本的平均平方进行缩放。 似乎仅分析5个样本序列就无能为力了。 动画显示了SPM AR图表有时相对于An-score明显“失败”。 应该理解的是,AR模型的“通过零”转变的力矩不仅在瞬时频率的误差方面而且在瞬时振幅的误差方面都可能是困难的,尤其是在低频区域。
最后的几点评论。
- 根据经验,至少在平均频率范围内(基于采样频率),这两种方法通常都可以很好地估计瞬时频率。
- 吉尔伯特认为,An方法的结果相对较高的质量,其简单性以及易于理解和实施的“余地”,远远超过了转换过程可能遇到的困难。 高质量的吉尔伯特数字滤波器,特别是在很宽的频率范围内,可能具有不可接受的高阶。 在实现此变换的替代周期图方法时,必须考虑到傅立叶变换隐式暗示该过程已完成为周期性。 结果,可能需要以零显着完成该过程。 An-method的结果质量高是因为它在选定时刻的非常广泛的邻域中使用信息(严格来说-在过程的整个临时实施中),并且这种相同的属性使其难以实现该方法(例如,在实时工作时)。
- 如有必要,可以建议采取以下措施来改善AR方法的结果:
- 数据稀疏(采样率过高)
- 平均数的增加-邻域模型中涉及的“时间矩”的延长-具有大量行的跟踪矩阵X的构造。
- 增加AR模型的顺序。