👶🏼 🤣 🥪 小波分析。第三部分 🐭 👨‍🍳 ☺️

引言

使用PyWavelets库（根据MIT许可发布的免费开源软件）进行CWT分析时，在可视化结果方面存在问题。下面的清单显示了开发人员提出的可视化测试程序：

上市

import pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max()) # doctest: +SKIP plt.show() # doctest: +SKIP

当处理复杂的小波时，例如使用“ cmor1-1.5”，程序将产生错误：

 File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float

这个错误，以及选择刻度（宽度）以提供必要的时间分辨率的困难，使得特别是对于新手用户而言，研究CWT分析变得困难，这促使我撰写具有教育意义的文章。

本出版物的目的是考虑使用新的比例尺可视化模块来分析简单和特殊信号，以及在使用归一化方法，对数比例缩放和综合时，在时间序列分析中提供其他信息。

本文使用了出版物“数据分析的小波简介”中的信息。在出版物中给出的示例列表中，错误已得到修复，并且示例的每个列表都以其最终形式显示，这使您可以使用它而无需熟悉先前的示例。对于特殊信号的小波分析，使用了来自PyWavelets 样本数据库的数据。

小波比例尺是一维数据的二维表示。时间绘制在X轴上，标度显示在Y轴上-信号的小波变换结果对应于时间X处的信号幅度。信号的这种图形显示的分析值是时间分辨率显示在Y轴上，这提供了更多信息关于信号的动态特性。

小波-简单信号刻度图

1.带有高斯包络的余弦波（替换小波。您可以研究时间分辨率对比例的依赖性）：

上市

 from numpy import* from pylab import* import scaleogram as scg import pywt #  ,        #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) p1=10; periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(periodic1); ax1.set_xlim(0, len(time)) ax1.set_title("   ") fig1.tight_layout() ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w")) tight_layout() print("    :", scg.get_default_wavelet(), "(", pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")") show()

用于信号转换的小波函数：cmor1-1.5（复杂的Morlet小波）

现在，周期信号在点Y = p1处以水平连续带的形式出现，其强度根据周期信号的幅度而变化。

由于带宽不等于零，因此在检测中存在一些模糊性，这是由于小波没有检测一个频率而是检测一个频带这一事实。这种影响与小波带宽有关。

2.三个脉冲以增加的周期顺序添加（要考虑不同比例的周期性变化：多分辨率分析）：

上市

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg #          #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) pulses = zeros(ns, dtype=float32) steps = linspace(0, ns, 8) periods = [10, 20, 40] for i in range(0,3): step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2]) pulses += cos(2*pi/periods[i]*time) * step_mask fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); ax1.set_title("     "); ax1.set_xlabel("Time") fig1.tight_layout() ax2 = scg.cws(pulses, scales=scales, figsize=(7,3)) for i in range(0, 3): txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), bbox=dict(boxstyle="round4", fc="w")) ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) ax2.plot(steps[i*2+2]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) tight_layout() show()

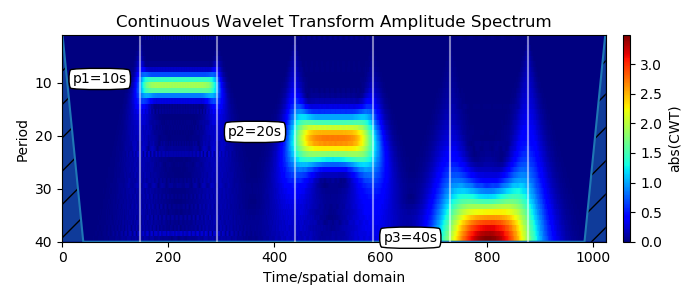
脉冲出现在预期位置Y中，与它们的周期性相对应，它们在频率和时间上都处于局部状态。条带的起点和终点与脉冲相对应。
带宽随周期的长度而缩放。这是小波变换的一个众所周知的属性：当比例增大时，时间分辨率减小。这也称为时间和频率之间的权衡。当您查看这种类型的频谱图时，您会进行大量的分辨率分析。

3.同时具有三个不同频率的周期性振荡（小波分析可以通过频率区分信号的成分，如果它们之间的差异很大）：

上市

 from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) allwaves = np.zeros(ns, dtype=np.float32) periods = [10, 20, 40] for i in range(0,3): allwaves += cos(2*np.pi/periods[i]*time) fig1, ax1 = subplots(1, 1, figsize=(6.5,2)); lines = ax1.plot(allwaves); ax1.set_title("  ") ax1.set_xlim(0, len(time)); ax1.set_xlabel("") fig1.tight_layout() ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2)) tight_layout() show()

4.非正弦周期信号（考虑周期为30秒的三角波信号的小波变换与先前考虑的信号之间的差异）：

上市

 from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) ptri = 30.0 # period in samples raising = 0.8 # fraction of the period raising triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising) # plot the signal fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(triangle); ax1.set_xlim(0, len(time)) ax1.set_title("triangle wave increasing 80% of the time with a 30s period") fig1.tight_layout() # and the scaleogram ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w")) txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w")) tight_layout() show()

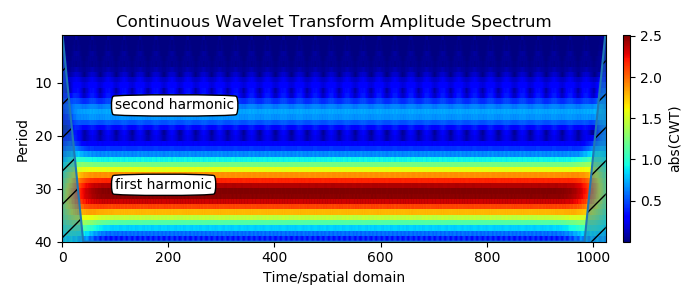
大频带是一次谐波。二次谐波恰好在一次谐波周期值的一半处可见。这是周期性非正弦信号的预期结果。模糊的垂直元素出现在二次谐波附近，二次谐波较弱，对于三角波，其幅度为第一次谐波的1/4。

5.平滑的脉冲（高斯）类似于真实的数据结构。（此示例显示了如何使用小波分析来检测局部信号随时间的变化）：

一系列具有不同sigma值的平滑脉冲：

$2 \ cdot \ sigma _ {1} = 2$
$2 \ cdot \ sigma _ {2} = 10$
$2 \ cdot \ sigma _ {3} = $ 2$

脉冲宽度

$\ omega _ {1} = 2$
$\ omega _ {2} = $ 2$
$\ omega _ {3} = $ 10$

上市

 from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) #       s1=1; s2=5; s3=10 events = [ns*0.1, ns*0.3, ns*0.7] bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + \ exp(-((time-events[2])/s3)**2) #      w1=1; w2=5; w3= 50 steps = ((time > events[0]-w1) & (time < events[0]+w1)) + \ ((time > events[1]-w2) & (time < events[1]+w2)) + \ ((time > events[2]-w3) & (time < events[2]+w3)) #   fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); ax1.set_title("Bumps"); ax2.set_title("Steps") lines = ax1.plot(bumps); ax1.set_xlim(0, len(time)) lines = ax2.plot(steps); ax2.set_xlim(0, len(time)) fig1.tight_layout() #   scales_bumps = scg.periods2scales(arange(1, 120, 2) ) fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3)); ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3) ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4) for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]: ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5) ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5) fig2.tight_layout() show()

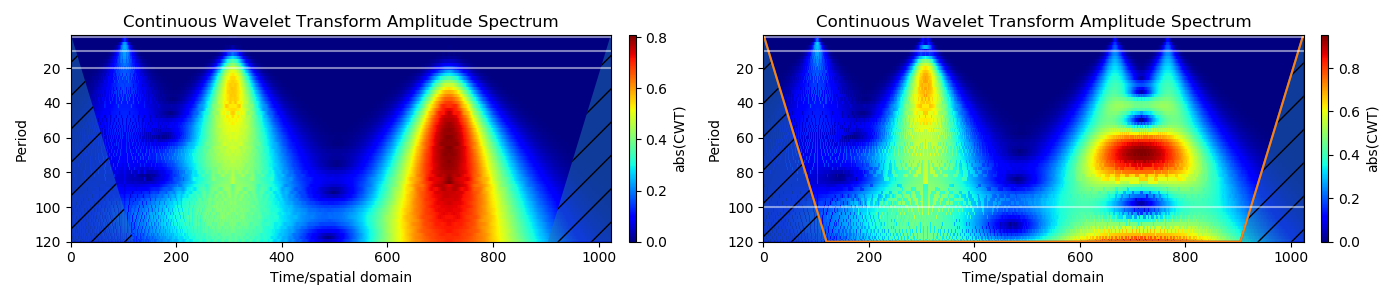
离散脉冲会在唾液曲线图上创建锥形结构，也称为影响锥。平滑脉冲（高斯）类似于真实的数据结构，并创建向大比例扩展的圆锥。水平引导线大致对应于时间段（2 s，10 s，20 s）。因此，脉冲类似于具有一个周期的周期信号。

6.噪声（在唾液图上显示噪声）：

上市

 from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) noise =random.sample(range(ns), ns) fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2)); ax1.set_title("  ") lines = ax1.plot(time, noise) ax1.set_xlim(0, ns) fig1.tight_layout() ax2 = scg.cws(noise, scales=scales, figsize=(7,2)) tight_layout() show()

噪声通常显示为一组元素，某些不规则现象看起来像真实数据的对象，因此，在使用真实数据时，必须小心，并在必要时检查噪声水平。每次启动程序时，较高的时间表将有所不同。

小波特殊信号波形

PyWavelets数据库包含二十个特殊的小波变换信号，这对研究和开发都是有用的。因此，我将列出一个清单，使您可以对所有二十个信号进行小波分析：

上市

 #!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from pylab import* import scaleogram as scg import pywt signals = pywt.data.demo_signal('list') signal_length=1024 for signal in signals: if signal in ['Gabor', 'sineoneoverx']: x = pywt.data.demo_signal(signal) else: x = pywt.data.demo_signal(signal, signal_length) times=[] signals=[] for time, sig in enumerate(x.real): times.append(time) signals.append(sig) scg.set_default_wavelet('cmor1-1.5') scales = scg.periods2scales( arange(1, 40) ) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(signals); ax1.set_xlim(0, len(times)) ax1.set_title("%s"%signal) fig1.tight_layout() ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); tight_layout() show()

我将仅给出多普勒信号的小波变换的一个结果：

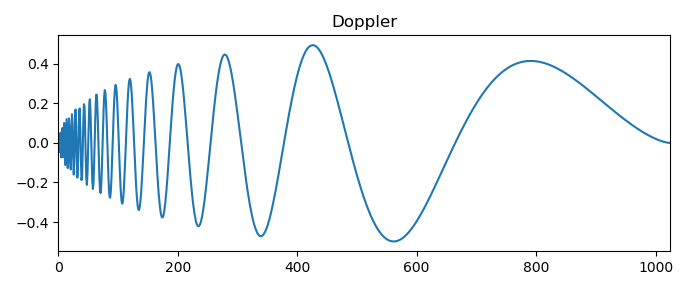
考虑了简单信号和特殊信号的最常见种类，这使我们可以切换到使用比例尺来解决时间序列分析的某些问题。

小波时间轴比例图

1.美国1969-2008年的CDC生育率数据（生育率数据包含周期性特征，包括年度尺度和较小尺度）：

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) fig = figure(figsize=(12,2)) lines = plot(births.index, births.values/1000, '-') xlim(datetime_lim) ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)"); xlim = xlim() ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

出现一条水平线，频率大约为7天。高值出现在刻度的边界附近，这是小波处理的正常行为。这些效果被称为影响锥，这就是为什么（可选）遮罩覆盖此区域的原因。

2.规范化（除去平均值是必不可少的，否则必须将数据边界视为会产生许多错误的圆锥形检测的阶段），否则必须删除平均值-births_normed = births-births.mean（ ）。

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()

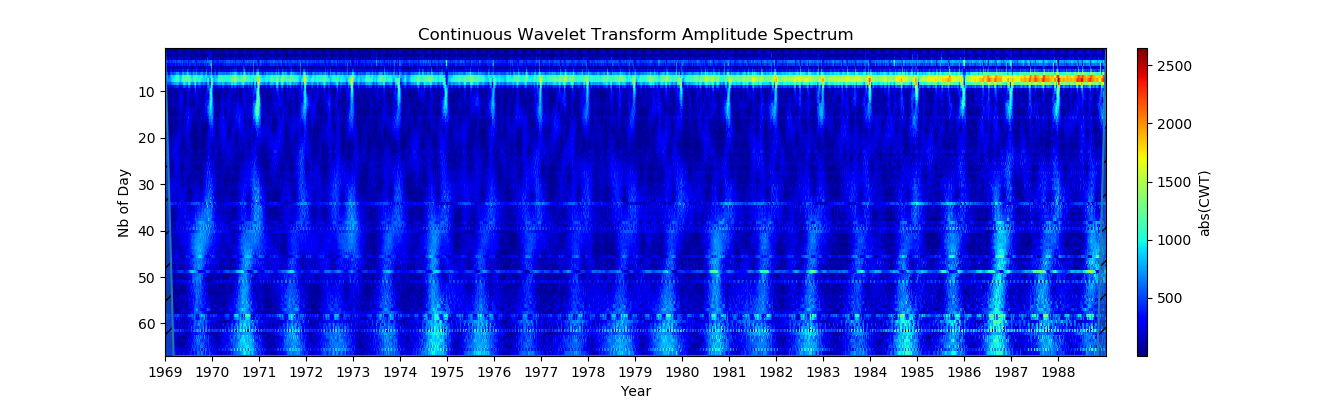
3.幅度比例的变化（要查看年度对象，请使用period2scales（）指定沿Y轴的比例）。

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day", clim=(0, 2500)) set_x_yearly(ax, len(births)) show()

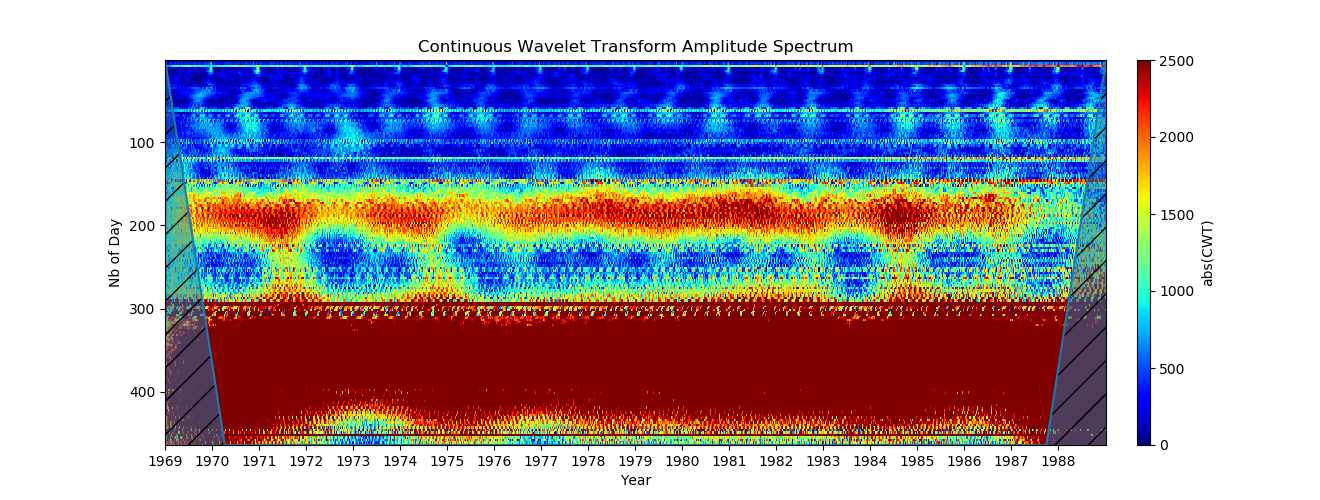
现在，通过clim =（0.2500）设置颜色图（Y轴）的幅度范围。振荡幅度的确切值取决于小波，但将保持接近实际值的顺序。这要好得多，现在我们可以很好地看到年度变化以及大约6个月的变化！

4.使用对数刻度（为了能够同时看到大和小的周期，最好在Y轴上使用对数刻度。这是通过xscale = log选项实现的。）

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) print("Number of available days:", len(births_normed)) show()

结果好得多，但是现在低周期值的像素沿Y轴拉长。

5.对数刻度上的均匀分布（要获得刻度上的均匀分布，必须将周期值均匀分布，然后转换为刻度值，如下所示：）：

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #  CWT  ,       cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowpropsf = dict(facecolor='yellow', shrink=0.05) text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), bbox=bboxf, arrowprops=arrowpropsf) show()

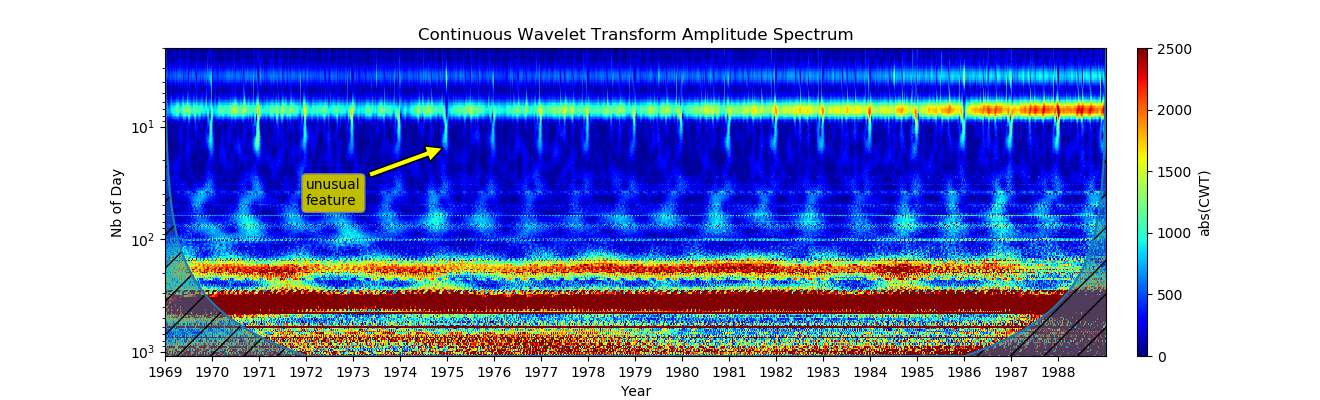
我们可以看到各种规模的信号变化。图表显示了每年的相等时间段。

6.突出显示时间线的一部分（检查工件或丢失的数据以检查时间线标记之间的中间数据）：

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) #    : 1974-1976 fig = figure(figsize=(12,4)) lines =plot(births.index, births.values/1000, '-') xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01")) ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 ) show()

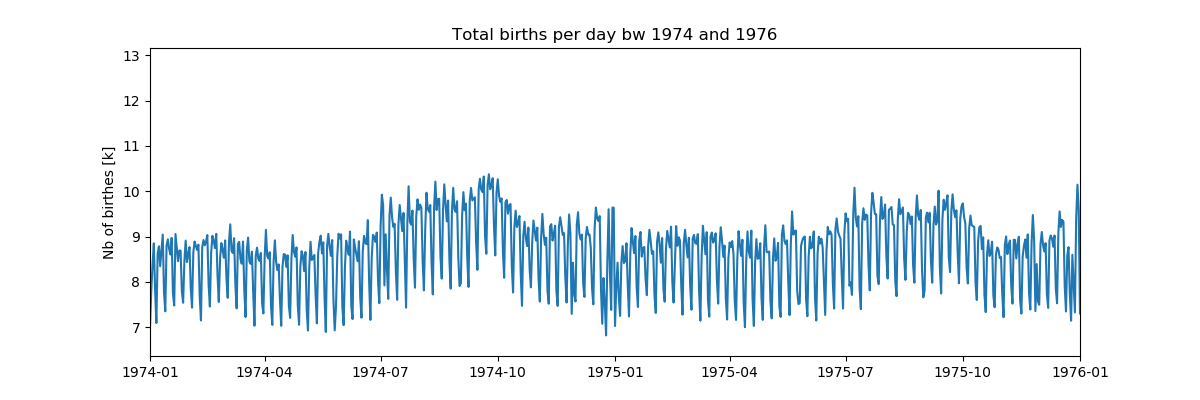
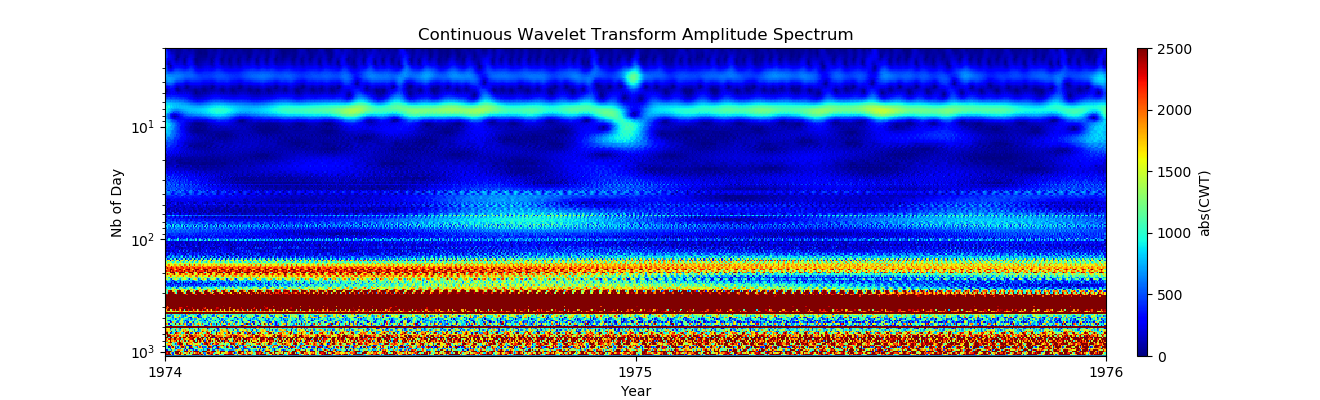乍一看，每周的模式看起来非常均匀，但是在圣诞节那天发生了一些事情，让我们再次来看一下这段时间：

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) # :  1975    1976  fig = figure(figsize=(12,4)) lines = plot(births.index, births.values/1000, '.-') xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01")) ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 ) show()

现在很明显，这是今年年底的结果：

圣诞节：12月23/24/25日的出生人数异常偏低，这些天与每周的时间表有所不同。
有12月的数据，这与1月1日和2日的受影响日期的某些值一致，这些日期通常少于个人事件

7.综合（根据标准化数据构建图表，对所有刻度都具有更好的可读性）：

上市

 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5") bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowprops = dict(facecolor='white', shrink=0.05) arrowprops2 = dict(facecolor='yellow', shrink=0.05) for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), (365, "one year"), (365*2.8, "long trends")]: text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), bbox=bbox, arrowprops=arrowprops) text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), bbox=bbox2, arrowprops=arrowprops2) text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), bbox=bbox2, arrowprops=arrowprops2) show()

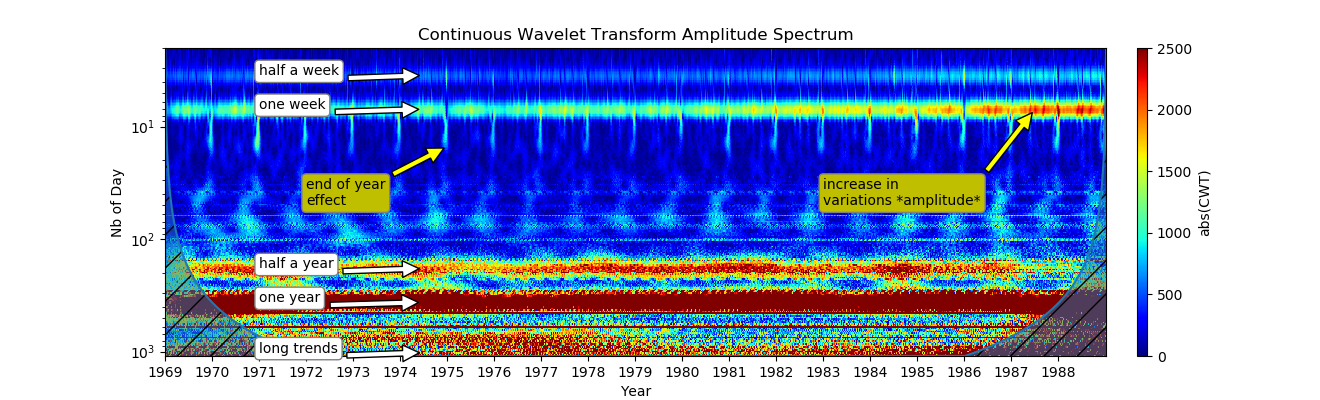CWT在很短的时间内揭示了很多信息：

几十年来，每周一次的变化显示出医院的习惯；

在80年代，每周指标有所增加，这可能是由于医院工作习惯的变化，生育率的变化或人口的简单变化引起的；

下半年频段显然是二次谐波。在3到1个月的区域中出现模糊模式，这可能是由于三次谐波引起的，因为年度波动非常大。它也可能是假期对生育能力的影响，可能需要进一步研究；

在圣诞节和1月1日注意到了年底的影响。这可能是另一种频率方法看不见的。

结论：

在此出版物中，我们看到了信号变化的基本形式如何转换为比例图。然后，使用一个按时间排序的数据集的示例来逐步演示CWT如何应用于标准数据。

可以将上述技术扩展为分析网络流量并检测对象的异常行为。 CWT是一种功能强大的工具，越来越多地用作神经网络的输入，可用于创建新功能来分类或检测异常。

每个示例都是作为一个独立的程序实现的，它使您可以为自己的任务选择一个示例，而无需深入研究之前和之后的示例。用户可以尝试每个程序开头给出的列表中的任何wavelet-函数，例如mexh或gaus5。分别为示例1：

PS对于清单的实际使用，我将给出其中使用的模块的版本：

 >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2

对于* .csv文件中的一组独立数据，我带了数据结构（在一列中）：
年，月，日，性别，出生
日期1969,1,1，F，4046
1969,1,1，M，4440
1969,1,2 ，F，4454
1969.1.2，M，4548
...
对于版本0.24.1的熊猫，您将需要显式注册matplotlib转换器。

要注册转换器：

 from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

小波分析。 第三部分

引言

小波-简单信号刻度图

小波特殊信号波形

小波时间轴比例图

结论：

More articles:

小波分析。第三部分