ARA：用于查找直线上最大点数的算法

最近，我遇到了一个经典的面试问题：搜索一条直线上（在平面上，整数坐标）上的最大点数。 穷举搜索的想法立即浮现在我的脑海，它在O（n ^ 2）中具有明显的时间复杂性，但是在我看来，应该还有其他东西，至少在O（n * log（n））中有其他选择。 。 半小时后，发现更好的东西！



_{有关输入输出示例问题的更详细说明，请参见GeeksForGeeks和LeetCode}

最初，我注意到您可以轻松地仅针对水平或垂直线解决问题，只需将字典中每个点的X / Y相加即可。 其他的线有什么区别？ 只是一个斜坡？..但是可以修复！

因此，我认为通过旋转它们可以多次遍历整个点列表。 并获得O（n）中的解！ 虽然系数很大。 我真的希望我没有发明自行车:)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

可视化，看起来像这样：
_{我的第一个自制GIF，请不要骂:)}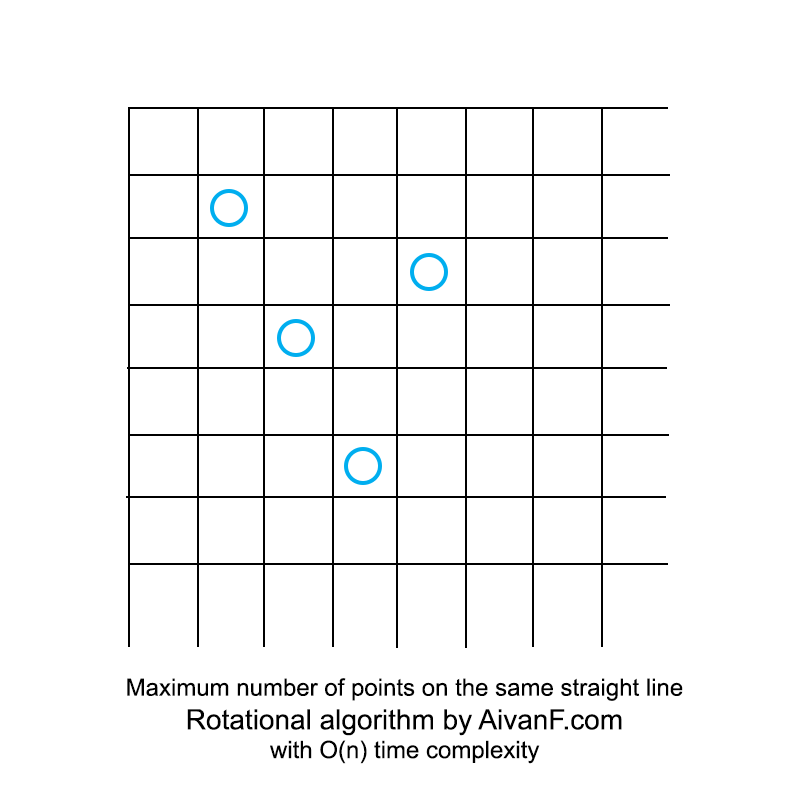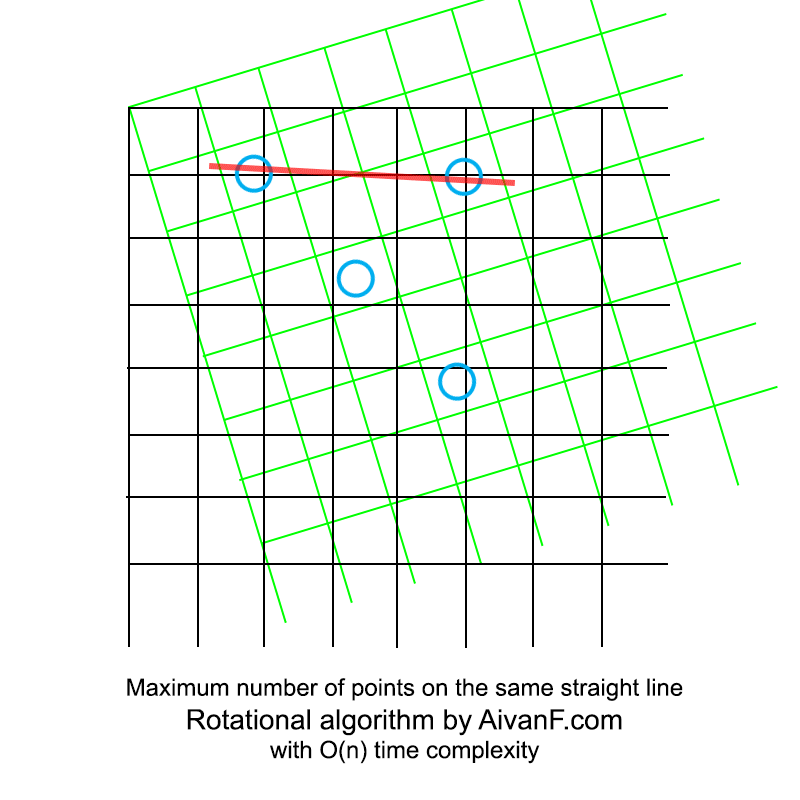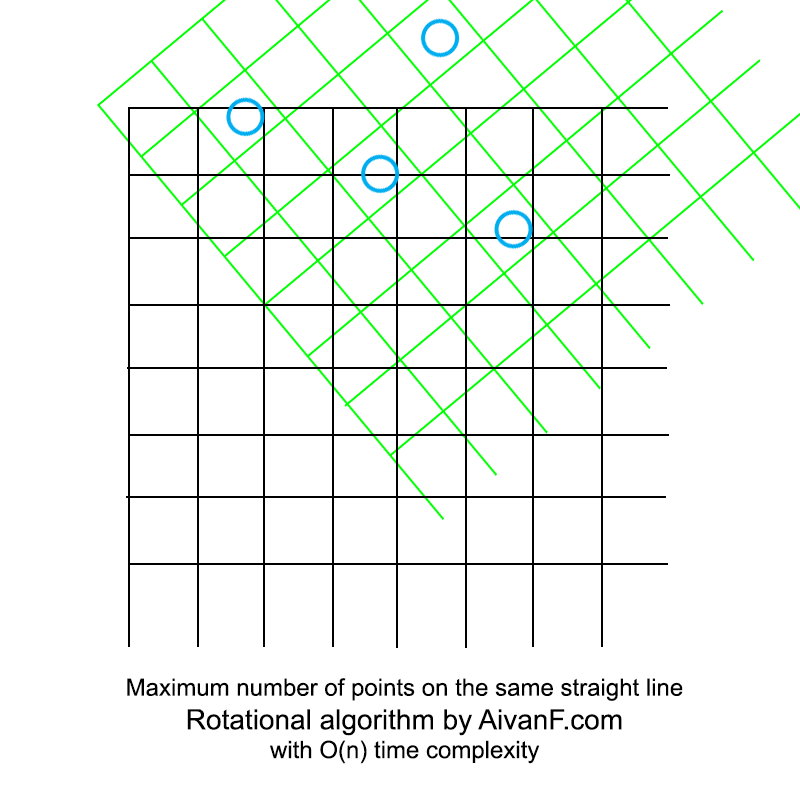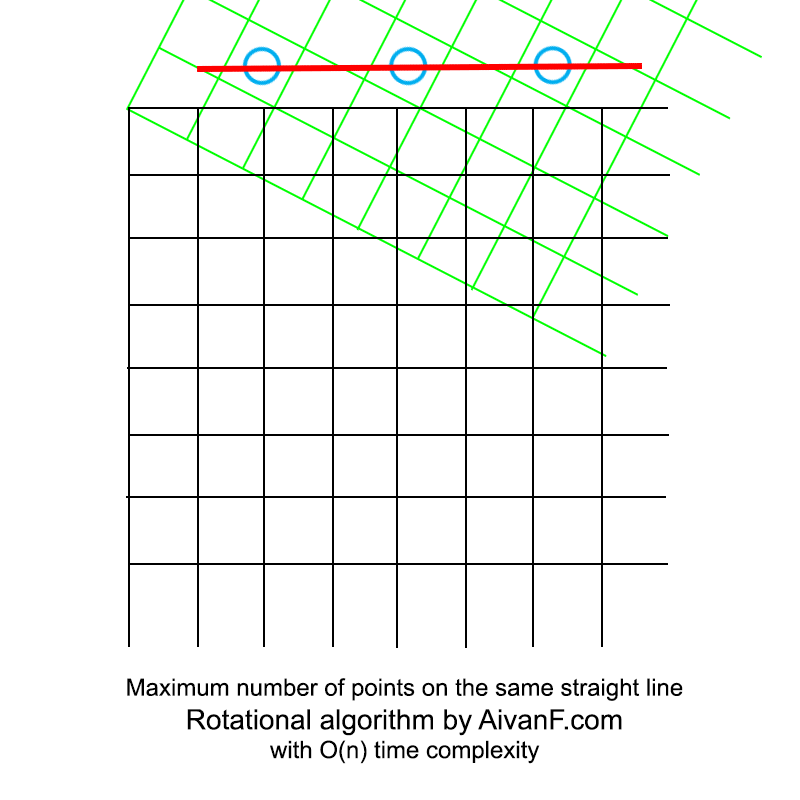



有趣的是，随后的穷举搜索实现占用了更多的代码行。

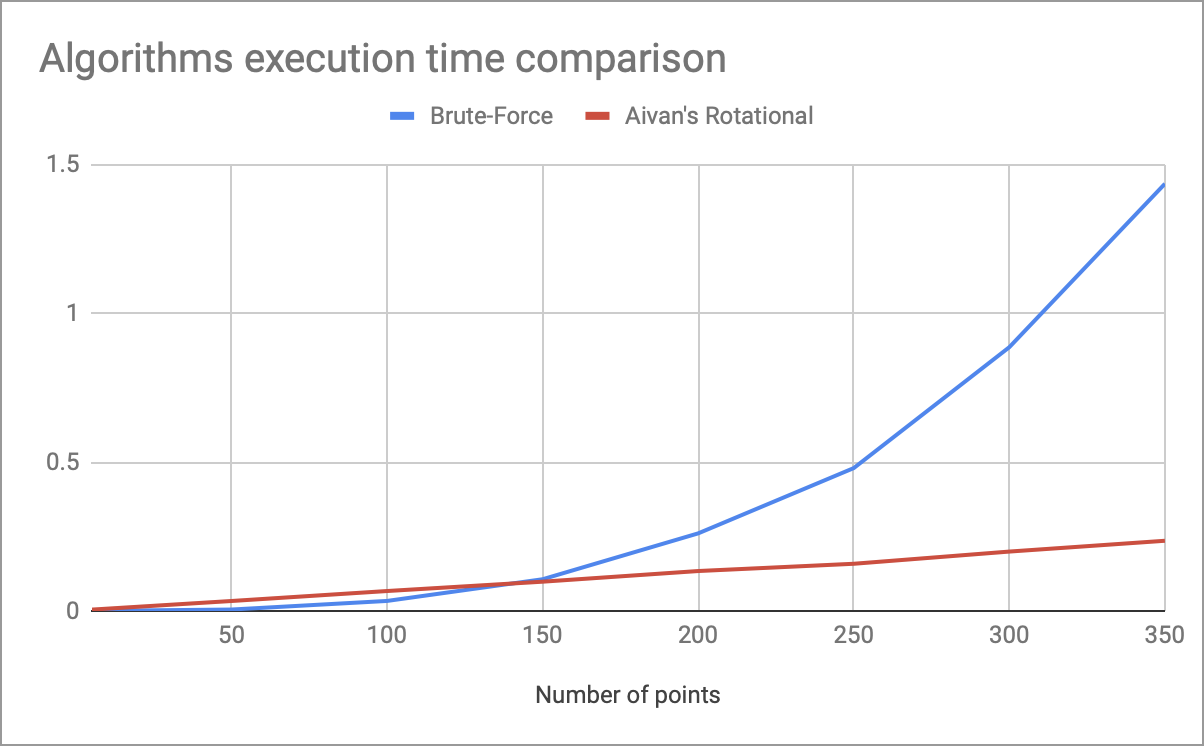
标头中包含带有旋转算法运行时间测量值以及根据点数进行的完整枚举的图形。


大约150个点显示了时间线性复杂度的优势（使用上面代码中的系数）。 结果，该算法具有以下缺点：

• 精度不是绝对的。
• 小点集上的运行时间很长。
  _{通常，通过选择合适的系数可以很容易地纠正这一问题：对于简单的集合，ROT_COUNT = 36而不是2000就足够了，这可以将代码加速50倍以上。}

并具有以下优点：

• 它可以使用分数坐标来平稳工作。
• 时间复杂度是线性的，这在大型数据集上很明显。

此处提供带有测量值的表格。 带有算法和各种检查的项目的完整源代码在GitHub上 。

更新资料 我想再次指出，该算法既有优点也有缺点，我不主张将其作为蛮力的理想替代品，我只是描述了一个有趣的可能替代方案，在某些情况下可能更合适。