
嗨,habrozhiteli! Marcos Lopez de Prado分享了他们通常隐藏的内容-他二十年来使用的最赚钱的机器学习算法来管理最苛刻的投资者的大量资金。
机器学习几乎改变了我们生活的方方面面; MO算法执行的任务直到最近才得到可信赖的专家的信任。 在不久的将来,机器学习将主导金融,算命将成为过去,投资将不再是赌博的代名词。
借此机会参加“机器革命”,因为它足以使人们熟悉第一本书,该书提供了与金融相关的机器学习方法的完整而系统的分析:从财务数据结构开始,标记财务系列,权衡样本,区分时间序列...最后以整个部分致力于对投资策略进行正确的回测。
摘录。 了解风险策略
15.1。 相关性
投资策略通常根据持有的头寸来执行,直到满足以下两个条件之一为止:1)使头寸获利的条件(获利)或2)使头寸亏损的条件(制止亏损)。 即使该策略未明确声明止损,也总是存在隐性的止损限额,在该限额下,投资者将无法为自己的头寸融资(追加保证金),也不会因未实现亏损的增加而遭受损害。 由于大多数策略具有(显式或隐式)这两个退出条件,因此通过二项式过程对结果的分布进行建模是有意义的。 反过来,这将帮助我们了解下注率,风险和支出的哪些组合不经济。 本章的目的是帮助您评估策略何时容易受到上述任何数量的微小变化的影响。
考虑一种策略,该策略每年产生n个分布均匀,相互独立的下注,其中下注i∈[1,n]的结果Xi是利润π> 0,概率为P [Xi =π] = p,损失–π的概率为P [Xi = –Π] = 1-p。 您可以将p想象成二元分类器的准确性,其中肯定的结果表示押注机会,而否定的结果则意味着失去机会:对正确的陈述进行奖励,对错误的陈述进行惩罚,对否定的结果(无论是对还是错)没有任何回报。 由于下注{Xi} i = 1,...,n的结果是独立的,因此我们将计算每个下注的期望时刻。 一个投注的预期获利为E [Xi] =πp+(–π)(1- p)=π(2p-1)。 方差是
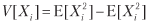
在哪里
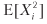
=π2p+(–π)2(1-p)=π2,因此,V [Xi] =π2-π2(2p-1)2 =π2[1–(2p-1)2] =4π2p(1- p ) 对于每年n个相同分布且相互独立的费率,年平均夏普比率(θ)为
注意,由于支出是对称的,因此π如何平衡上述方程式。 与高斯情况一样,θ[p,n]可理解为重新定标的t值1。 这说明了即使是很小的事实
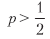
对于足够大的n,可以提高夏普比率。 这是高频交易的经济基础,其中p可以略高于.5,成功进行交易活动的关键是增加n。 夏普比率是准确性的函数,而不是正确性的函数,因为错过机会(否定陈述)不会得到直接奖励或惩罚(尽管太多否定陈述会导致n变小,这会使夏普系数降至零)。
例如,对于
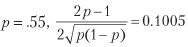
并且要达到平均每年2的夏普比率,每年需要396下注。 清单15.1通过实验验证了这个结果。 图15.1显示了不同投注频率下的Sharpe比率与准确性的关系。
清单15.1 夏普比率与下注次数的关系
out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out)
对于给定的Sharpe系数(θ),该方程式非常清楚地表达了精度(p)和频率(n)之间的权衡。 例如,为了使仅产生每周费率的策略的年平均夏普比率为2(n = 52),将需要相当高的准确性p = 0.6336。
15.3。 不对称付款
考虑一种策略,该策略每年产生n个分布均匀的相互独立的下注,其中下注i∈[1,n]的结果Xi为π+,概率为P [Xi =π+] = p,结果π–(π– <π+ )发生的概率为P [Xi =π_] = 1-p。 一个投注的预期获利为E [Xi] =pπ+ +(1- p)π– =(π+-π–)p + π–。 色散为V [Xi] =,其中
最后,我们可以将前面的方程解为0≤p≤1并得到
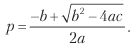
其中:
a =(n +θ2)(π+-π–)2;
b = [2nπ-θ2(π+-π-)](π+-π–);

注意:清单15.2使用在Google App Engine云服务
live.sympy.org上运行的Python SymPy Live shell验证了这些符号操作。
清单15.2 使用SymPy库进行符号操作
>>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v)
上面的方程式回答了以下问题:对于以参数{π–,π+,n}为特征的给定交易规则,达到等于Sharp比率θ*的精确度p是多少? 例如,为了在n = 260,π– = –.01,π+ = .005时得到θ= 2,我们需要p = .72。 由于大量下注,p的很小变化(从p = .7到p = .72)将夏普系数从θ= 1.173提升到θ=2。另一方面,这也告诉我们,该策略容易受到小影响。 p的变化 清单15.3实现了预期精度的推导。 在图。 15.2显示了假定精度与n和π–的关系,其中π+ = 0.1,θ* = 1.5。 当阈值π–对于给定的n变得更负时,对于给定的阈值π+,需要更高的度数p才能达到θ*。 对于给定的阈值π,随着n的数量变小,对于给定的π+,需要更高的p度才能达到θ*。
清单15.3 估算精度的计算
def binHR(sl,pt,freq,tSR): ´´´
对于以参数{sl,pt,freq}为特征的给定交易规则,达到等于tSR的Sharpe比率所需的最低精度是多少?
1)输入
sl:止损阈值
pt:利润门槛
频率:每年的下注次数
tSR:目标年度平均夏普比率
2)退出
p:达到tSR所需的最低精度p
´´´
a =(频率+ tSR ** 2)*(pt-sl)** 2
b =(2 *频率* sl-tSR ** 2 *(pt-sl))*(pt-sl)
c =频率* sl ** 2
p =(-b +(b ** 2-4 * a * c)**。5)/(2. * a)
返回p
清单15.4求解估计的下注频率n的θ[p,n,π–,π+]。 在图。 15.3显示了取决于p和π–的估计频率,其中π+ = 0.1,θ* = 1.5。 当阈值π–对于给定的度数p变得更负时,对于给定的阈值π+,需要更大的数字n才能达到θ*。 对于给定的阈值π,随着度p变小,对于给定的阈值π+,需要更大的数量n才能获得θ*。
清单15.4 计算估计的下注频率
def binFreq(sl,pt,p,tSR): ´´´
对于以参数{sl,pt,freq}为特征的给定交易规则,每年需要多少次下注才能以准确度p达到Sharp系数tSR?
注意:带有自由基的方程,请检查无关的解。
1)输入
sl:止损阈值
pt:利润门槛
p:准确度p
tSR:目标年度平均夏普比率
2)退出
频率:每年所需的下注次数
´´´
freq =(tSR *(pt-sl))** 2 * p *(1-p)/((pt-sl)* p + sl)** 2#可能无关
如果不是np.isclose(binSR(sl,pt,freq,p),tSR):返回
返回频率
»这本书的更多信息可以
在出版商的网站上找到»
目录»
摘录小贩优惠券可享受25%的折扣-
机器学习支付纸质版本的书后,将通过电子邮件发送该书的电子版本。