👋🏼 🤱🏿 🛡️ 交换排序算法的比较 🖕🏾 👩🏻 👂🏽

本文讨论了用于对交换进行排序的各种选项，还描述了一个带有排序示例的简单图形应用程序（ processing.js ）。

阅读之前，建议您阅读valemak用户的文章：

→ 交换分类
→ 气泡排序和所有所有
→ 愚蠢的排序和其他一些更聪明

气泡排序

最简单的选择是从第一个元素到最后一个元素迭代数组，以交换（如果需要）相邻元素。

→ 在这里检查

为了移动滑块，您需要单击左下角的灰色按钮。
当您单击按钮时，将滑块向右移动一级

slider++;

接下来，我们检查：是否到达数组的末尾（然后跳到开头），然后比较（互换）相邻元素

按钮代码

 //  //  void mousePressed() { if(boolButton) { counter++; if(mods[slider].rectHight < mods[slider-1].rectHight) { vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[slider].rectHight; mods[slider].rectHight=vTemp; } } } // void mouseReleased() { if(boolButton) { slider++; if(slider>=moduleSize) { slider=1; } } }

Processing.js使用Java数据结构，然后将代码转换为javascript（ link ），因此，负责渲染元素和初始化实例的Module类实例数组的声明是这样发生的

代号

 Module[] mods; ... mods[0] = new Module(1*30, 30); mods[1] = new Module(2*30, 50); mods[2] = new Module(3*30, 10); mods[3] = new Module(4*30, 60); mods[4] = new Module(5*30, 20); mods[5] = new Module(6*30, 100); mods[6] = new Module(7*30, 80); mods[7] = new Module(8*30, 70); mods[8] = new Module(9*30, 90); mods[9] = new Module(10*30, 40);

绘制void draw（）的主要功能是一个无限循环，其中对类实例进行排序

 for (Module mod : mods) { mod.display(); }

添加randFoo（）函数，该函数返回随机值。为了确保这些值不会重复，我们将它们添加到listRand列表中的ArrayLis t中，并在randFoo（）函数中，检查新的随机数是否在listRand列表中

 int randFoo(){ newRand = int(random(1,11)); if(!listRand.contains(newRand) ) listRand.add(newRand ); else newRand=randFoo(); return newRand; }

→ 在这里检查

像素排序

像素排序（此处）是气泡排序的一种实现。
我们将较暖/较亮的像素移到一侧，将较暗/较冷的像素移到另一侧

 void draw(){ while (i <= height) { c=get(i,j); //    cTemp=c; //      i++; //     c=get(i,j); //     if(cTemp>c) { //   fill(c); //    rect(i-1,j,1,1); fill(cTemp); rect(i,j,1,1); } } if(mousePressed) { if(j>=width) j=0; } //      if(i >= height) {j++; i=0;} }

→ 在这里检查
要开始排序，请单击图片并按住按钮。
您可以在此处阅读有关像素排序的更多信息。
官方频道The Coding Train上有关像素排序的视频

限制器和标志

如果不迭代已排序的项目，则可以减少迭代次数。为此，在数组的末尾添加一个限制器 ，它将在每次迭代后移至数组的开头

 if(slider>=limiter) { slider=1; limiter--; if(limiter<1) limiter=1; }

→ 在这里检查

另一种减少胸围数量的方法可以在文章冒泡排序（Wikipedia）中找到。如果在数组通过期间我们从未切换过相邻元素，则对数组进行排序并完成循环（艾弗森条件）。

添加一个flag flag ，当我们遇到几个需要互换的元素时会出现。如果标志升高，则再次遍历数组。如果没有，请结束循环。标志的状态显示在控制台中。

检查相邻元素

 if(mods[slider].rectHight < mods[slider-1].rectHight) { flag=true; //   vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[slider].rectHight; mods[slider].rectHight=vTemp; }

→ 在这里检查

如果将限制器放在左侧，并使用具有限制器的元素作为参考/最小值，我们将按选择进行排序。

添加将要加载最小值的min变量。假设最初最左边的元素是最小的：在数组的第一遍，如果元素小于最小值，那么我们将该元素本身保存在变量min中。

 if(mods[slider-1].rectHight < min){ min=mods[slider-1].rectHight; }

然后交换第一个元素和最小元素

 if (mods[limiterL-1].rectHight>min) { vTemp= mods[limiterL-1].rectHight; mods[limiterL-1].rectHight=mods[slider-1].rectHight; mods[slider-1].rectHight=vTemp; }

如果滑块到达数组的右边缘，则限制器将向右移动一级，并且滑块将移至限制器

 if(slider==moduleSize){ if(limiterL<moduleSize) limiterL++; min=mods[limiterL-1].rectHight; incPaddle=limiterL-1; }

→ 在这里检查
如果在搜索开始时我们比较（互换）数组的当前元素和最右边的元素，则可以减少度量的数量

 if(mods[limiterL-1].rectHight>mods[moduleSize-1].rectHight) { vTemp=mods[limiterL-1].rectHight; mods[limiterL-1].rectHight=mods[moduleSize-1].rectHight; mods[moduleSize-1].rectHight=vTemp; }

那么你就不能检查数组的最右边的元素

 //if(slider==moduleSize){ if(slider==moduleSize-1){ //if(limiterL<moduleSize) limiterL++; limiterL++; min=mods[limiterL-1].rectHight; slider=limiterL-1; } // slider++; if(slider<moduleSize) slider++;

→ 在这里检查

在这里，您可以通过添加最大元素max来按降序添加数组右侧部分的排序-我们通过选择获得振动筛排序。请参阅文章末尾有关振动筛分类的部分。

快速分类

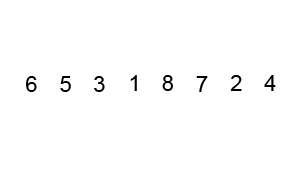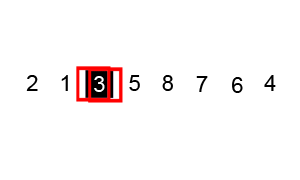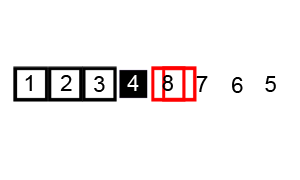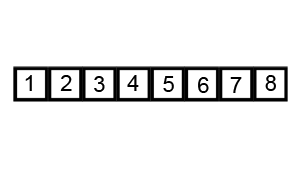
支持元素选择机制还用于快速排序。该算法涉及选择初始参考元素，并与数组的所有其他元素进行比较。算法的执行时间取决于初始元素的选择。在上面的gif中，起始元素是数字3 。您可以在文章（Wikipedia）中阅读有关选择起始支持元素的更多信息。
有关处理和p5.js语言的官方youtube频道上提供了有关快速排序的视频，您可以在此处看到算法的可视化。
如果第一个元素是基本元素，则可以在其前面插入比基本元素小的元素，然后将数组分为两部分，左边的元素将比右边的基本元素小-更多。对于这种方法，请参见下面有关按插入排序的部分。

矮人排序

本质上，侏儒会查看下一个和先前的花盆：如果它们的顺序正确，他会向前走一个花盆，否则他会交换它们并向后退一个花盆。

升起标志后，将滑块的坐标保存在变量limiterR中，然后逐步将滑块返回到数组的开头

 slider--;

一旦到达数组的开头，请重置标志并将滑块与我们保存在变量limiterR中的坐标一起放入单元格中

 if(slider==0){ flag=false; slider=limiterR; }

→ 在这里检查

通过更改此算法，我们得到“ 按插入排序 ”。
在按插入排序时，选择引用/最小元素，然后在数组的未排序部分中，选择小于引用的元素，并将其插入到引用之前

让我们拥有与先前元素之间的最小元素交换位置，直到参考元素为止，依此类推。插入参考的前面。
添加条件

 if(slider==limiterR-1 && mods[slider-1].rectHight<mods[limiterR-1].rectHight){ flag=false; slider=limiterR; }

→ 在这里检查

与限幅器比较

该分类选项可以任意地称为“矮人插入分类”。
将限制器放在左侧，我们将使用带有限制器的元素作为参考/最小值，就像在排序选择中一样。
如果当前元素大于最小值，则将滑块向右移动

 if(mods[slider-1].rectHight > mods[limiterL-1].rectHight) slider++;

如果当前元素小于最小值，则将滑块的坐标保存在变量limiterR中，并分步将滑块返回到数组的开头，如gnome排序

 vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[slider-2].rectHight; mods[slider-2].rectHight=vTemp; slider--;

一旦到达数组的开头，请重置标志并将滑块与我们保存在变量limiterR中的坐标一起放入单元格中

 if(flag && slider==limiterL) { flag=false; slider=limiterR; }

如果滑块超出右边缘，则将限制器向右移动一级，将滑块返回到限制器

 if(slider==moduleSize+1) { limiterL++; slider=limiterL+1; }

→ 在这里检查

在这里，您可以通过bubble方法添加当前元素和以下元素的比较（交换）

 if(slider<moduleSize)if(mods[slider].rectHight<mods[slider-1].rectHight){ vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[slider].rectHight; mods[slider].rectHight=vTemp; }

→ 在这里检查

“快速”插入排序

在该算法中，数组被支持元素分为两部分。
假设第一个元素为引用：从第二个开始，将数组的元素与引用进行比较（如果元素小于引用）

 if(mods[slider-1].rectHight < mods[pivot-1].rectHight)

在引用之前插入找到的元素

 if(mods[slider-1].rectHight < mods[pivot-1].rectHight){ flag=true; //   vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[slider-2].rectHight; mods[slider-2].rectHight=vTemp; }

如果标记升起，则将滑块向左逐步移动，直到遇到支撑元件

 if(flag){ slider--; if(slider<pivot){ flag=false; //   pivot++; slider=pivot; } }

T.O. 数组分为两部分，左侧-元素小于引用，右侧-更多

→ 在这里检查

如果在每次枚举之后，支撑元素的坐标都保存在ext中。 axissArr数组，然后当参考元素到达右边缘时，我们得到一个按级别/步骤排序的数组。每个下一级的元素将大于上一级的元素。级别的边界将包含在add中。 shaftsArr数组
每次您单击按钮时，我们都会将ivotsArr数组输出到控制台

 for(int i=0;i<pivotsArr.length;i++){ print(" "); print(pivotsArr[i]); print(" "); }

将随机函数randFoo（）添加到程序的末尾。

→ 在这里检查

现在您需要分别对每个级别的元素进行排序（仅添加结束循环的条件）

→ 在这里检查
可以将这种排序描述为按级别排序。
，因为在每次枚举之后，数值数据都是按级别排列的，所以每个下一个级别的数量都超过了上一个的数量。

奇偶排序

我们将滑块移动两步，比较相邻元素

 slider=slider+2;

T.O. 我们比较元素0和1、2和3、4和5、6和7等。
如果滑块到达数组的边缘，则使限制器向左移动一步，然后滑块向数组的开头移动。
接下来，我们比较元素1和2、3和4、5和6、7和8等。
到达限制器后，我们将其向右移动一步，将滑块放在数组的开头。

→ 在这里检查

整理梳子

设滑块在数组的开头，右定界符在结尾。比较（交换）元素。我们将限制器向左移动一步，并将其索引保存在limiterStore变量中

 if(limiter==moduleSize) { limiter = limiterStore-1; limiterStore = limiter; slider=1; }

逐步将带止点的滑块移动到数组的末尾

 if(limiter!=moduleSize) { //  limiter     limiter++; slider++; }

作为限制器到达数组的末尾，将滑块放在数组的开头，然后将限制器放入limiterStore-1

 if(limiter==moduleSize) { limiter = limiterStore-1; limiterStore = limiter; slider=1; }

→ 在这里检查

摇床排序

将左限制器limiterL添加到数组的开头。
当滑块到达右侧限制器limiterR时 ，使标志标记上升，然后限制器向左移动一级。此外，当标记升起时，滑块会逐步移回左侧限制器限制器L-限制器会向右侧移动一步-滑块会向右逐步移动

按钮代码

 //  void mouseReleased() { if(boolButton) { if(!flag) { slider++; if(slider==limiterR) { flag=true; limiterR--; if(limiterR<=limiterL+1) limiterR=limiterL+1; } } if(flag) { slider--; if(slider==limiterL) { flag=false; limiterL++; if(limiterL>=limiterR-1) limiterL=limiterR-1; } } } }

→ 在这里检查

摇床按选择排序
使用右限制器和左限制器将气泡添加到气泡排序中。每次向右移动滑块时，我们都会检查（交换）较大的值-当前元素或限制器

 if(mods[slider-1].rectHight<mods[limiterL-1].rectHight){ vTemp= mods[slider-1].rectHight; mods[slider-1].rectHight=mods[limiterL-1].rectHight; mods[limiterL-1].rectHight=vTemp; }

当滑块到达右限制器R时，右限制器向左移动一级，左限制器向右移动一级，滑块返回左限制器

 if(slider>=limiterR){ limiterL++; slider=limiterL; limiterR--; }

→ 在这里检查

PS：此处描述的应用程序使研究算法和数据结构更加有趣 。
大量算法和数据结构的另一种可视化。
本文提到了另一个站点，您可以在其中查看如何通过不同算法对数据进行排序。
本文对气泡排序的复杂性进行了评估。
可以在这里，这里，这里，这里阅读有关复杂性评估的更多信息。

交换排序算法的比较

气泡排序

像素排序

限制器和标志

快速分类

矮人排序

奇偶排序

整理梳子

摇床排序

More articles: