
最近,我遇到了意大利科学家
所做的
有趣的工作,关于运气和机会在我们生活中的作用被大大低估了。 不幸的是,我没有找到俄语的完整版本(也许我看上去很糟糕?),但我真的很想与我的英语流利的同志分享我的读物。 因此,他rolling起袖子,着手进行手工翻译。 作者Alessandro,Alessio和Andrea允许将其发布在公共领域,因此,如果您有兴趣,欢迎关注。
作者
- A. Pluchino-意大利卡塔尼亚大学物理与天文学系和国家核物理研究所卡塔尼亚分院; alessandro.pluchino@ct.infn.it
- A. E. Biondo-意大利卡塔尼亚大学经济与商业系; ae.biondo@unict.it
- A. Rapisard-意大利卡塔尼亚大学物理与天文学系和国家核物理研究所卡塔尼亚分院; 维也纳复杂系统研究中心; andrea.rapisarda@ct.infn.it
注解
高度竞争的西方文化模式源于这样一种信念,即:主要
是精英制(专才制
是管理原则,根据这一原则,最有能力的人,无论他们的社会出身和财务状况如何),其领导力强的西方文化模式源于以下信念:取决于个人素质,例如才华,才智,技能,机智,勤奋,毅力,勤奋或冒险。 有时我们愿意承认,一定的运气也可以在取得重大的物质成功中发挥作用。 但是,实际上,外部力量在个人成功故事中的重要性常常被低估了。 众所周知,人口中的智力(或一般而言,才干和个人素质)具有高斯分布,而价值分布(通常被视为衡量成功的标准)通常在多数人贫穷且贫困时遵循幂定律(帕累托定律)。亿万富翁的数量微不足道。 具有正常水平(才华或才智)的正态分布输入与输出的恒定分布之间的差异表明,在幕后某处存在不可见的成分。 在本文中,基于一个非常简单且基于玩具代理的模拟,我们假设该组件是普通事故。 特别是,我们表明,人生的成功确实需要一定的才能,而最有才华的人几乎从来没有达到财富的最高峰,而被平庸的,但更成功的人格所取代。 据我们所知,这种矛盾的常识结果(尽管在许多文献中各行之间都暗含了假设)是第一个进行定量评估的结果。 这使您可以重新审视基于已取得的成功水平评估优劣的有效性,并强调将过多的荣誉或资源传播给从长远来看可能比其他人更成功的人们的风险。 使用该模型,我们还考虑并比较了几种行为假设,以显示最有效的公共研究资金策略,目的是提高精英水平,多样性和创新性。
1.简介
在许多物理,生物或社会经济复杂的系统中,普遍存在的幂律依赖性可以看作是其动态特性与尺度不变的拓扑结构的紧密关系的独特数学特征[1,2,3,4]。 在社会经济背景下,根据帕累托[5,6,7,8,9]的工作,众所周知,财富分配具有权力依赖的特征,其特征强烈拉长的形状反映了我们社会贫富之间现有深渊的深度。
最近的一份报告[10]显示,今天的贫富差距比我们所担心的要大得多:八个人拥有与36亿人一样的财富,这些人构成了人类最贫穷的部分。 在过去的20年中,已经开发了几种理论模型,这些模型在概率论和物理统计的背景下计算值的分布,通常采用具有简单内部动力学的多主体建模的形式[11、12、13、14、15、16、17]。
朝这个方向进一步发展,如果我们将个人财富视为成功的衡量标准,则可以说,人与人之间极不对称和不平等的分配是由于他们天赋,技能,能力,才智,能力,毅力,勤奋或有目的性。 这种隐含的假设是所谓的精英主义范式的基础:它不仅影响我们的社会如何提供就业机会,荣誉和名望,而且还影响政府采取的将资源和资金分配给那些被认为是最富裕的人的战略。尊贵的人物。
但是,先前的结论似乎与已证实的数据有很大不同,上述数据表明,人的上述属性和素质在整个人口中呈正态分布,即,相对于该平均值而言,对应于对称的高斯分布。 例如,通过智商测试测得的智力与以下模式相对应:平均智商为100,但没有人的智商为1000或10000。同样的情况也适用于以工作时间计的工作:某人的工作量超过平均水平,另一人的工作量大于平均水平。更少,但没有人比其他人工作十亿倍。
但是,在我们这个时代,越来越多的证据表明,机会,运气或通常是随机因素在决定我们的个人和专业事务的成败中起着根本作用。 尤其是,事实证明,所有科学家在其职业生涯中都有相同的机会发表突破性的工作[18]。 那些姓氏首字母更接近字母开头的人更有可能担任部门主管的职位[19]; 由于与通货膨胀的“出版或死亡”机制有关的现象不断增加,科学家收集的文献计量指标的分布可能变得随机且毫无意义[20]; 某人在按字母顺序排序的列表中的位置对于确定受场所数量限制的公共服务的访问可能很重要[21]; 中间名的首字母可以提高对智力的评估[22]; 与名字复杂的人相比,名字易于发音的人得到的评价更高[23]; 那些名字听起来比其他人更贵族的人是领导而不是下属[24]; 有男性昵称的妇女在法律界比较成功[25]; 世界各地人之间大约一半的收入差异仅由其居住国和各自国家内的工资分配来解释[26]; 成为董事的可能性在很大程度上受到您的姓名和出生月份的影响[27、28、29]; 创新思想是我们大脑细胞中随机反应的结果[30]; 而且甚至患上癌症的可能性,很可能破坏一个出色的职业生涯,在很大程度上取决于失败[31,32]。 关于终生生殖成功这一主题的最新著作证实了这种说法,表明如果性状的改变会影响整个人口的命运,那么特定个体的生活往往取决于运气。
近年来,许多学者,包括统计学家和风险分析师Nassim Taleb [35,36],投资策略师Michael Mobussin [37]和经济学家Robert Frank [38],在多本畅销书中研究了运气与金融交易技巧之间的关系,商业,体育,艺术,音乐,文学,科学等许多领域。 他们得出的结论是,随机事件在生活中的作用比许多人想象的要大得多。 实际上,他们并不认为成功不取决于人才和努力,因为在竞争激烈的领域或市场中,例如“胜利者承担一切”,此时我们生活和工作的地方,生产力最高的人几乎总是与众不同有才华和努力。 他们仅得出结论,才干和努力还不够:您还需要在正确的时间放置在正确的位置。 简而言之,运气也会产生影响,尽管成功人士几乎总是低估它的作用。 这是由于以下事实:随机性通常以一种不明显的方式起作用,因此很容易将显示成功的事件进行比较是不可避免的。 塔勒布(Taleb)称这种倾向为“极好的谬论” [36],社会学家保罗·拉扎斯菲尔德(Paul Lazarsfeld)提出了“有偏见的回顾”一词。 社会学家和网络科学先驱邓肯·沃茨(Duncan Watts)在他的最新著作《一切都是显而易见的:知道答案之后》 [39]中指出,神话般的妄想和偏颇的追溯性都吸引了一种特殊现象,在这种现象中,人们看到了异常成功的结果,认为它们无疑是努力和才能的产物。 但是,成功主要是通过复杂而相互交织的步骤而产生的,每个步骤都取决于先前的步骤:如果每个步骤都不相同,则整个职业或人生道路几乎肯定也会有所不同。 这个论点也是基于几年前瓦茨本人与其他作者合作进行的一项创新性实验研究的结果[40],其中在人工音乐市场上以前未知的歌曲的成功并未显示出与作品本身的质量相关。 当然,这会极大地增加任何预测的复杂性,如另一项最近的研究[41]所示。
在本文中,我们将使用基于代理的统计方法来尝试定量地确定运气和才能在成功职业中的作用。 在第2节中,基于最少的假设,即人才分配的高斯性质[42]和成功与失败的乘性动力学[43],我们提出了一个简单的模型,我们将其称为“人才与运气”模型(TPU),它模仿了一群人在40年的工作生涯中的职业发展。 该模型表明,实际上,随机性在确定最成功的个人方面起着根本作用。 真实的事实是,正如人们可能期望的那样,与准备不足的人相比,有才华的人更有可能在自己的生活中变得富有,成名或显赫。 但是,由于这种不太直观的解释,从统计学上讲,具有普通水平的才能的普通人注定会比最有才能的人更成功(即位于成功的某些动力分配的末尾),前提是他们成为财富的最爱。一生 如参考文献[35、36、38]所示,经常遇到这个事实,但是据我们所知,它是在这项工作中首先被建模和测量的。
具有普通才能的人的成功令人质疑“精英主义”范式,以及所有那些为所在领域中最优秀的人提供更多奖励,机会,荣誉,名望和资源的战略和机制[44,45]。 事实是,在大多数情况下,对某人的才能的所有评估都是在事实发生之后进行的,仅是通过查看他/她在社会的特定领域(例如体育,商业,金融,艺术)的活动或取得的结果来进行的,科学等 这种类型的误导性评估会导致因果关系的替代,将最简单,最成功的人视为最有才华的人[46,47]。 根据这种观点,先前的研究警告了类似类型的“近端精英”,并显示了在许多不同环境(例如管理,政治和财务)中基于随机样本的其他策略的有效性[48,49,50,51,52, 53、54、55]。 在第3节中,我们将应用我们的方法并概述在科学研究的背景下如何分配公共资金。 我们研究了各种分配策略的后果,其中包括“接近”的精英管理,目的是探索新的方法,以同时提高社会上最有才华的人的成功率和政府支出的总效率。 我们还将总体上考察以教育和收入水平(即外部因素取决于国家和人民所来自的社会层面)形式提供的环境所提供的机会对于增加成功的可能性的重要性。 最后的评论完成了工作。
2.型号
此外,我们基于少量假设,提出了一个称为“人才与好运”的代理模型,旨在描述在随机发生的成功和失败事件的影响下,一群人的职业发展。
 图1:用于模拟的初始参数示例。 本文介绍的所有模拟都是在NetLogo代理模拟环境中进行的[56]。 N = 1000人(代理人),他们具有不同程度的才能(才智,技能等),随机分布在201×201个具有循环边界条件的正方形世界中的固定位置上。 在跨越数十年的每次模拟过程中,它们都受到一定数量的N E成功(绿色圆圈)和不成功(红色圆圈)事件的影响,这些事件沿着随机轨迹在世界范围内移动(随机游走)。 在此示例中, NE = 500。
图1:用于模拟的初始参数示例。 本文介绍的所有模拟都是在NetLogo代理模拟环境中进行的[56]。 N = 1000人(代理人),他们具有不同程度的才能(才智,技能等),随机分布在201×201个具有循环边界条件的正方形世界中的固定位置上。 在跨越数十年的每次模拟过程中,它们都受到一定数量的N E成功(绿色圆圈)和不成功(红色圆圈)事件的影响,这些事件沿着随机轨迹在世界范围内移动(随机游走)。 在此示例中, NE = 500。我们认为
N个具有
T i才能(智力,技能,能力等)的个人在[0; 0; 1]围绕给定的平均
m T并以标准差
σT随机放置在具有循环边界条件(即环形拓扑)的正方形世界(见图1)内的固定位置上,并被一定数量的
N E所 “包围”事件(标有点),其中一些是成功的,没有其他事件(此模型中的中性事件没有考虑,因为它们对个体的生活没有重大影响)。 在图1中,我们以彩色圆点的形式显示了这些事件:绿色成功,相对百分比为
p L ,红色不成功,百分比为(
100-p L )。 事件点的总数
N E是均匀分布的,但是,当然,这样的分布在理想情况下仅对于
N E →∞是均匀的。 在我们的模拟中,通常会出现
N E≈N / 2 ,因此,在每次模拟开始时,世界各个区域都会随机出现大量成功或失败事件点,而其他地区则更为中立。 随后点在正方形矩阵(即世界)内的随机移动不会改变模型的这一基本特征,即对于不同的人来说,一生中成功或失败的事件数量不同,这并不取决于他们的个人才能。

图2:人才在人群中的正态分布(中值
m T = 0.6用垂直虚线表示,标准偏差
σT = 0.1-值
m T ±σT用两条垂直虚线显示)。 该分布在间隔[0; 1],并且在仿真过程中不会更改。
一个模拟运行检查了40年的工作寿命
P (20至60岁),时间步长
δt为6个月。 在模拟开始时,为所有代理赋予相同的资本
C i = C(0)Ɐi = 1,...,N ,表示他们成功/幸福的起始水平。 这种选择的明显目标是不给任何人最初的优势。 尽管坐席的才华不随时间而变,但他们的资本正在变化。 在此模型的开发过程中,即在特工生命的预期期间,所有事件点都会在世界各地随机移动,并且同时可能与某些特工的位置相交。 如果要详细介绍,每个事件点每次都沿随机方向覆盖2个部分的距离。 我们认为,如果圆内表示的事件点(半径为一个线段)以主体为中心,则该事件与个人存在相交(相交后事件点不会消失)。 ,
t (.., ),
A k :
- A k – , , A k .
- A k – , ( , [30], , ); , A k / , T k . C k (t) = 2C k (t − 1) , rand[0; 1] < T k , .., , .
- A k – , ; , A k / , .. C k (t) = C k (t − 1) / 2 .
( , ), , , , . , , , ( , ). , , , , . , «», « , ». , «» , , , , , , , , . , , .
2.1。
. , , , , , .
N = 1000
C (0) = 10 ( )
T i ϵ [0; 1],
m T = 0,6
σ T = 0,1 (. 2). ,
P = 40 , , ,
I = 80 .
N E = 500 ,
p L = 50%.
, () 3, , / , () (). , (b) ,
y© ≈ C −1,27 .
, , , , , : . , 4 500 , 20 44% , 10 . , «80/20», 80% 20% , 20% 80% . , , , , , / , . ?
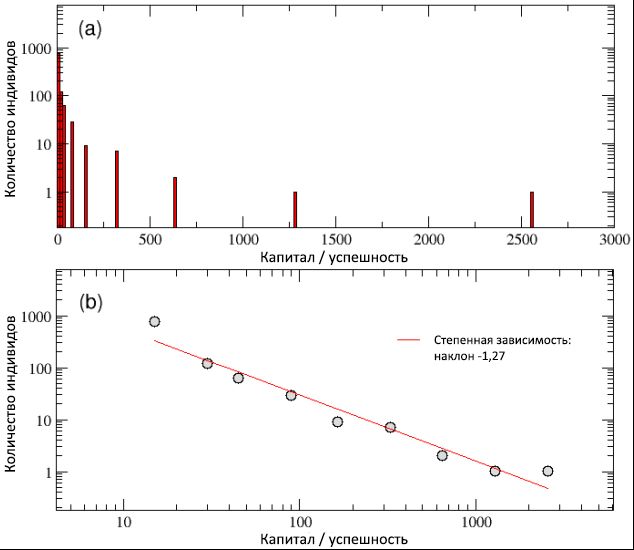
3: / , (a) (b) . , — (b) — −1,27. , / «80/20», 20% 80% .
4, (a) (b), , / , ( , (a) / – ). , , , , , . , ,
C max = 2560,
T* = 0,61,
m T = 0,6, (
T max = 0,89) / , 1 (
C = 0,625).
, , , , : , . , . ,
T > T* C ≈ 20; , / 128 , / , , . , , , , . , .
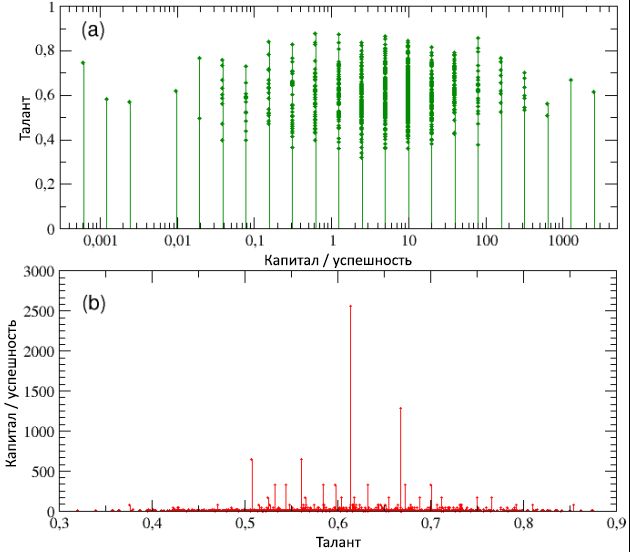
4: () / ( , ) – , , , . (b), , / – , ,
C max = 2560, ,
m T = 0,6, / ,
C = 1 ,
C (0). .
5 , , / . (a) , ( , , , , , ). , (b), , . , , , , . , , © (d), , 0,64 0,48, 1,35 1,66, , , , 10 15. , 16% «» , , 40% - ( ).
/ , , , 40 (80 , 6 ) . , , 6. (a) 5, , , , .
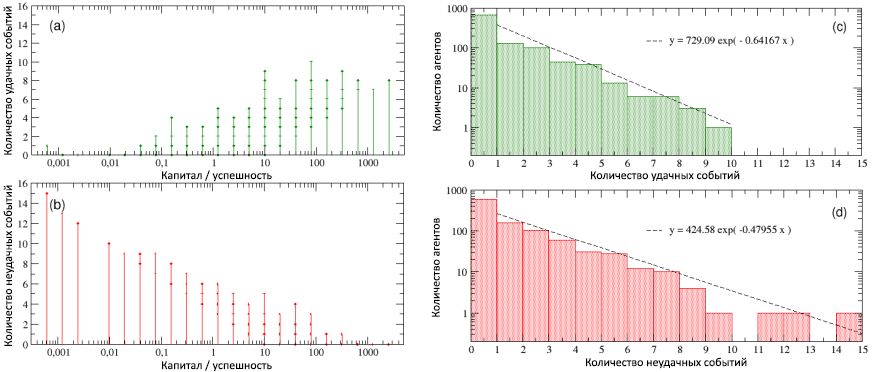
5: (a) (b) , / . : , . , - , , / . © (d) , , . , ).
( ) (a) 6, , , , , ( ), ( ), , 30 40 (.. 40- ) , 10 (.., 5 ) ,
C = 320
C max = 2560.
, ( ) (b) , , , , , / ,
C = 0,00061. ,
T = 0,74, , . , . , , ( ), , , , .
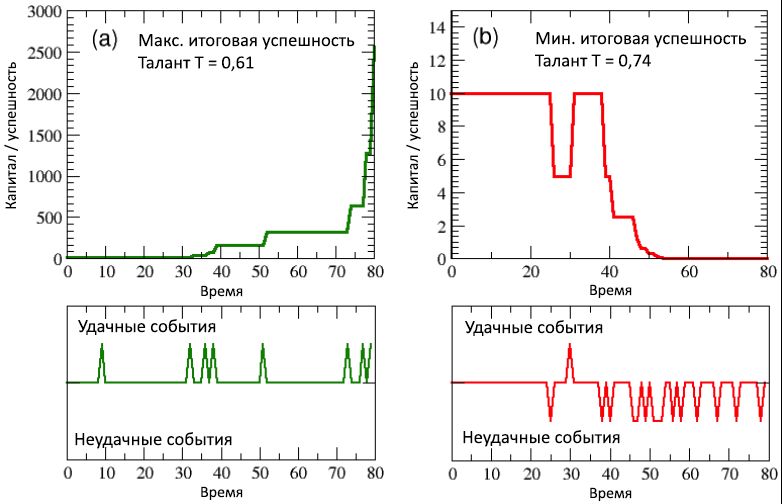
6: (a) / (b) , , ( 80 , .., 40 ). , .
(- NetLogo , ,
Open ABM), , , , , , , , .
2.2。
在本小节中,我们介绍了平均100多次运行的一般模拟结果,每个运行都从不同的,随机选择的初始条件开始。 控制参数的值与上一部分相同:
N = 1000个人,
m T = 0.6,
σT = 0.1(对于人才的正态分布),
I = 80次迭代(每个代表
δt = 6个月的工作寿命) ),
C (0)= 10个单位的初始资金,
NE = 500个事件点,成功事件的百分比
p L = 50%。
在图7的图表(a)中,以对数标度显示了作为100次运行所收集的所有代理之间总资本/成功总数的总分布,并通过角系数为-1.33的幂律曲线很好地描述了该分布。 因此,在多次运行中,无论规模大小,都可以在一次运行中观察到资本恒定的特性,从而导致个人之间的高度不平等以及帕累托规则“ 80/20”。 实际上,富人(成功)和穷人(不成功)之间的差距甚至扩大了,因为最富裕人士的资本现在已超过40,000个单位。
通过查看图7的方案(b),可以最好地估计此结果,其中仅将最成功的个人的总资本
C max显示为人才的函数。 在100次运行中均显示出最佳结果。 人才
T 最佳 = 0.6048的代理商,与达到峰值资本
C 最佳 = 40960的人才分布的中位数(
m T = 0.6)几乎相吻合,得分最高。人才
T max = 0.91,获得的资本
C max = 2560,仅是
C best的 6%。
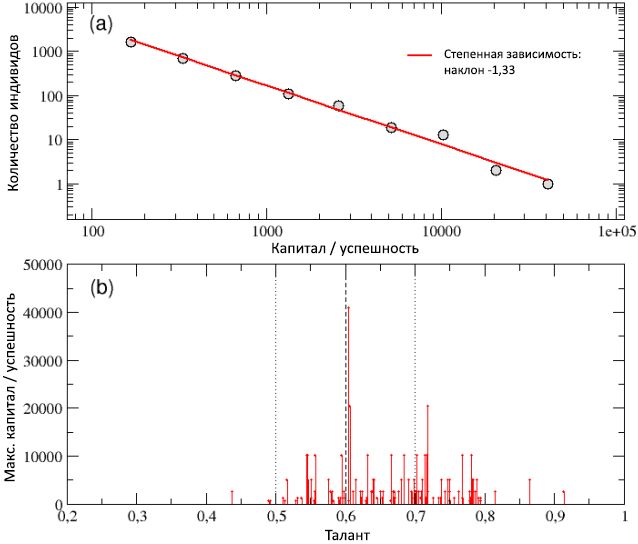
图7:方案(a)-对于具有不同随机确定的初始条件的人群,在100多次运行中计算的总资本/成功的分布。 该分布可以通过具有-1.33斜率的幂曲线来描述。 方案(b)-在每100次运行中,最成功的个人的总资本
C max ,显示为其才能的函数。 平均而言,具有中等天赋的人比那些具有低天赋或中度天赋的人更成功,并且最成功的人通常是有天赋的特工,而偶尔也只有最有才华的人。
m T的值以及
m T ±σT的值分别以垂直虚线和虚线的形式显示。
为了更详细地考虑这种观点,在图8(a)中,我们绘制了以100次运行计算的最佳绩效人才的分布情况。 显然,分布沿人才轴向右移动,平均值为
T av = 0.66>
m T-一方面,这证实了要取得显著成功,通常需要适度的高才能; 但是,另一方面,这也表明,这种条件几乎是远远不够的,因为才华最高的特工(即
T >
m T =
2σT或
T > 0.8)才是表现最好的代理商在3%的情况下,他们的资本/成功从未超过
C best的 13%。
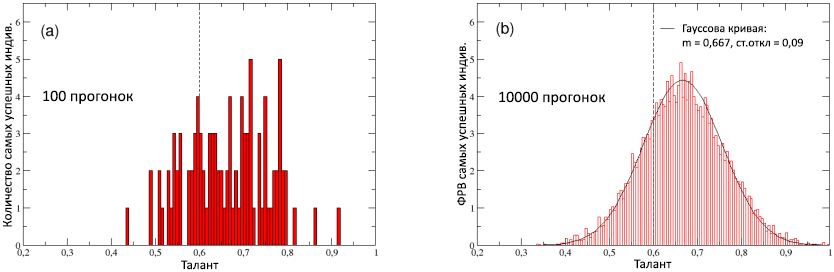
图8:(a)在每100次跑步中,最成功的人物(表现最佳)的才华分布。 (b)最成功的人才的概率分布函数(RFF),以10,000次计算:用正态分布很好地描述,中位数为0.667,标准偏差为0.09(实线)。 为了进行比较,显示了总体中人才的初始正态分布的中位数
m T = 0.6,在两个方案中均以垂直虚线表示。
在图8的图(b)中,为了了解其真实形状,计算了10,000次运行的相同分布(减少到总面积以获得FRF):看起来它符合平均
T av = 0.667的高斯曲线
G(T)标准偏差为0.09(实线)。 当然,这证实了与最初的分配相比,绩效最佳的人才的分配相对于人才的轴线向右移动。 更准确地说,这意味着条件概率
P (
C max |
T )=
G(T)dT可以在表现最佳的人中找到区间为[
T ;
T + dT ]随着人才
T的增长而增长,在大约中度人才
T av = 0.66附近达到峰值,然后在人才价值较大时急剧下降。 换句话说,在成功之上找到一个中等才华的人的可能性要比在那里找到一个有天赋的人的可能性高。 请注意,在人才是成功的主要原因的理想世界中,预计
P (
C max |
T )将成为
T的增长函数
。 因此,我们可以得出结论,观察到的高斯形式
P (
C max |
T )证明了运气比天赋对获得极高成功水平的重要性更大。
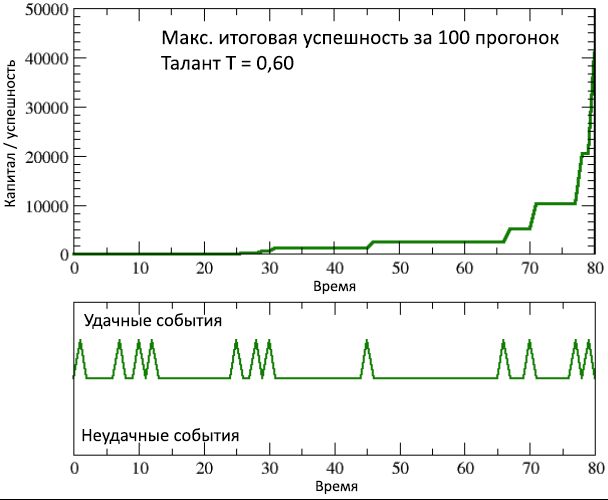
图9:在100次模拟运行中,最成功的人(但同时具有中度天赋)的成功时间/资本的变化与她一生中发生的相应异常成功事件的序列相比。
从100次运行中比较最有才华的人的平均资本/成功率
C mt≈63 ,而与之接近中位数
m T的人的相应平均
C约为≈33
。 在这两种情况下,我们都发现指标很低(即使大于初始资本
C (0)= 10),但
C mt >
C at的事实表明,尽管在成功的顶部找到中度才华的人的可能性更高,与那些天赋高的人相比,每次跑步中最有才华的人平均比中度天赋的人更成功。 另一方面,从100多次平均运行来看,人才
T > 0.7(即高于中位数的标准差)和最终成功/资本
C 结束 > 10的个体比例(考虑到所有具有人才
T > 0.7(每次跑步平均≈160),我们发现这一比例为32%-这意味着我们人口中最有才华的人的平均表现相对较小,因为其中三分之一的总资本超过了原始资本。
无论如何,在100次模拟运行中表现最好的代理人的才能
T best = 0.6(与中位数完全匹配),而最终成功
C best = 40960(比
C mt高 650倍)是
无可辩驳的 。在2/3的最有才华的人中,比
C end <10的成功率高出4000倍以上。 最后,这仅仅是因为他比其他人幸运。 从图9可以看出,无条件的幸运表明了他的资本/成功在他的工作生涯中的增长,以及一系列令人印象深刻的成功(也是成功的)事件,尽管缺乏杰出的才能,但他仍然能够在自己的职业生涯中获利职业。
总结一下,在这一点上,我们发现尽管TPU模型非常简单,但它似乎能够考虑到许多特征,正如引言中所述,这是我们社会中财富分配和成功的高度不平等现象,这明显与高斯的人才分配形成了鲜明的对比。人。 同样,以定量形式表示的模型表明,出色的人才不足以保证成功的职业生涯,相反,才华横溢的人往往会达到成功的顶峰-这是现实生活中经常观察到的另一个“条件性事实” [35,36,38]。
与有才华的人相比,有才华的人能够(经常)获得更大的荣誉和成功,直觉地解释了这种情况会发生的一个关键方面是,运气存在着一个隐藏的且常常被低估的作用,这很明显从我们的模拟中可以看到 但是要了解我们研究结果的真正含义,重要的是要区分宏观和微观观点。
实际上,在微观层面上,遵循TPU模型的动态规则,有天赋的人比具有中等才能的人更容易获得高水平的成功,因为他有更高的把握机会的能力。 因此,从个人的角度出发,我们应该得出这样的结论:不能(按定义)影响成功事件的出现,增加成功可能性(在任何水平的人才)的最佳策略是扩大个人活动,产生想法,交流与其他人一起寻求多样性和相互丰富。 换句话说,成为一个愿意与他人保持联系的胸怀宽广的人,是成功事件的最大可能性(这将取决于个人的才能)。
另一方面,从整个社会的角度来看,在成功的顶峰遇见有天赋的人的可能性要比在那里找到极有才能的人高得多,因为前者更大,而且由于运气好,他们总体上具有统计意义尽管他们自己先验的可能性较低,但取得巨大成功的优势。
在下一节中,我们将考虑这种宏观层面的观点,探索我们的模型提供的机会,以便更详细地研究更有效的战略和政策,以提高人口中最有才华的人的平均绩效水平,采用更富有成效的方式分配奖励和资源。 实际上,我们期望,任何能够提高作为我们社会进步与创新引擎的最有才能的人的水平的政策都会产生累积的有益影响。
3.有效的运气平衡策略
上一节中给出的结果与导言中记录的经验证据明显吻合,后者引证了人称的假设,即人才,技能,能力,才智,勤奋或毅力的自然差异是成功的唯一原因。 正如我们已经表明的那样,运气也有影响并且可以发挥关键作用。 讨论的实质是,由于个人素质难以衡量(在许多情况下,很难用精确的术语来确定),优点管理策略通常用于分配荣誉,财务或奖励,通常基于私人结果,以个人财富或成功来衡量。 结果,由于积极的反馈机制,这种策略影响了进一步行动,以增强和提升最成功人士的财富/成功,这类似于“致富致富”过程(也称为“马修效应” [57,58,59]) ,结果不公平。
假设有一个政府资助的研发理事会,其中有固定数量的资金可供支配。 对于提高平均研究效率,将有什么更有效的方法:只给少数几个毫无疑问的优秀科学家提供大笔资金,或给许多显然更多的普通科学家提供小笔资金? 最近的一项研究[44]基于对相关出版物的科学意义的四个指标的分析,发现意义与资金筹集仅具有弱的正相关关系。 特别是,对于大笔赠款持有人来说,美元的意义要低一些,获得资助增加的科学家的意义并未适当增加。 该研究的作者得出结论,科学意义(如出版物中所反映的)仅在融资方面具有弱势,并建议旨在多样化思想而非“卓越”的融资策略可能更具生产力。 后来的一篇论文[60]表明,无论是在产生的文件数量上还是在其科学重要性上,集中的研究经费通常都会导致边际收益的下降,而且研究经费最多的研究人员在有效性和科学意义上也不突出。 通常,根据最近的另一项发现[18],得出这样的结论并不令人惊讶,该发现指出,根据有影响力的出版物来衡量,其重要性随机分布在许多科学家的出版物中。 换句话说,运气很重要,如果运气的影响超出我们想承认的范围,则精英管理策略的效果就不及预期的不足为奇,特别是如果我们试图欣赏后验的优点时,这一点也就不足为奇了。 在先前的研究中[48、49、50、51、52、53、54、55],已经出现了针对这种“近端精英”的警告,表明基于随机选举的替代策略在管理,政治和金融领域的有效性。 根据这种观点,TPU模型显示了如何提高世界上大多数幸运的人才的最低成功水平,而偶然发现常常会带来重要的成就。
3.1。 偶然发现,创新和有效的融资策略
“偶然发现”一词在文学中对历史事实的引用中被广泛使用,这表明研究人员在寻找其他东西时,常常是纯粹地偶然地做出了意外和有用的发现[61,62]。 从巧合上发现的发现故事一长串:从亚历山大·弗莱明(Alexander Fleming)的青霉素到玛丽·居里(Marie Curie)的放射性,从射电天文学家亚诺·彭齐亚斯(Arno Penzias)和罗伯特·伍德罗·威尔逊(Robert Woodrow Wilson)的宇宙微波背景辐射,到石墨烯Andrei Geim和Konstantin Novosyolov。 这是最近的一个例子:在简单的内窥镜检查中偶然发现了一个人体中充满液体的通道网络,这个先前未知的器官显然促进了癌细胞的扩散[63]。 因此,许多人认为,由好奇心驱动的研究应始终得到资助,因为没有人真正能够提前知道或预测他们将导致什么[64]。
是否可以量化随机发现的重要性? 模拟随机发现的最有效方法是什么? 它可以采用许多不同的形式,并且难以限制和量化。 这就是为什么直到现在,学术研究仍将偶然的科学发现视为哲学概念的原因。 但是时代在变。 欧洲研究委员会最近向生物化学家Ohid Yakubu分配了170万美元的赠款,以计算科学中偶然发现的重要性[65]。 雅库布(Yakub)发现,随机发现可以分为四种基本类型[66],并且可能存在影响其外观的重要因素。 他的发现似乎与早期研究[67,68,69,70,71,72]的想法相吻合,后者认为追求优势和取代多样性的普遍接受的,显然是精英的策略似乎注定会失败。和无效的。 原因是他们先验地拒绝了最初看起来不太有希望的研究,但是特别是由于随机发现,这些研究可能使后验者具有难以置信的创新性。
从这个角度来看,我们想应用TPU模型,该模型自然地将运气(因此,是随机发现)表示为该策略的定量参数,以便研究本小节中各种融资方案的有效性。 尤其是,在如上所述的情况下,具有中等才干但很幸运的人通常比拥有更多天赋但不太幸运的人更成功,因此,评估融资策略对维持最低成功水平的能力(包括针对成功者)的有效性非常重要。最有才华的人,有望带来最创新和进步的想法。
从第2.2节中使用的相同初始参数开始,即
N = 1000,
m T = 0.6,
σT = 0.1,
I = 80,
δt = 6,
C (0)= 10,
NE = 500,
p L = 50%并进行了100次仿真可用的总资金资本
F T会根据各种标准定期分配给个人。 例如,可以发行财务:
- 平等分享(平等标准)以鼓励研究的多样性;
- 只有一定比例的最成功的(“最佳”)个人(精英标准),以前称为“近乎精英”,可以根据过去的表现在人与人之间分配资金。
- 在一定比例的最成功的个体中“溢价”分布,其余部分在其余部分中一小部分相等(混合标准);
- , ( ).
,
F T 5 , 40- ,
F T = 8 . . ,
P T , 100 ,
T >
m T + σ T , / , ..,
C end >
C (0).
, 2.2. , , , / . ,
P T0 ≈ 32%
T > 0,7 , , / , . , ,
P T P T0 , .
P * T = P T − P T0 . : 100 ,
P * T 2%. ,
P * T , 40 ,
E , ,
E = P * T / F T .
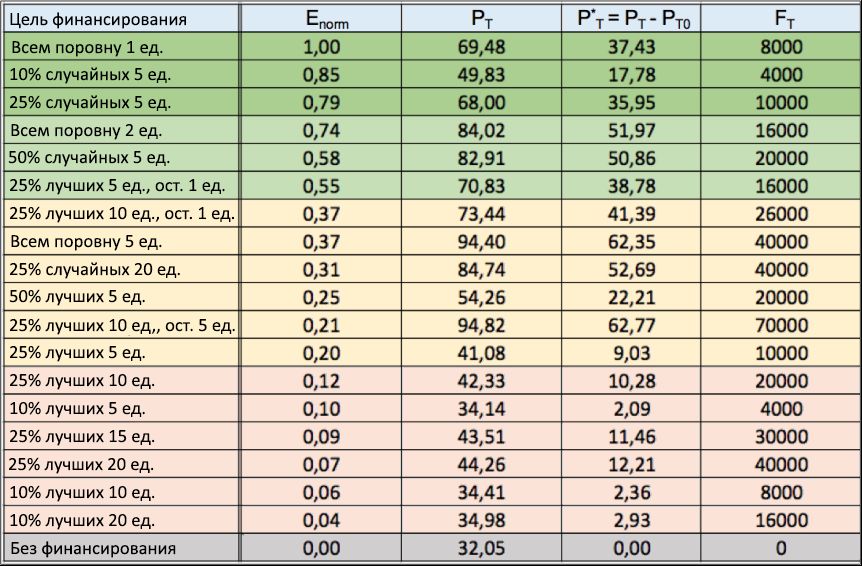
10: . (1 ),
E norm (2 ), . , , ,
P T P * T , « », 100 . ,
F T , .
, 10, (2- ), , (1 ),
P T (3- )
P * T (4- ). , ,
F T .
E E max , ()
E norm = E / E max . , ,
E norm = 0.
E norm 11.
P T , 2%,
E norm .
11, , ( ), ( ) , , , .
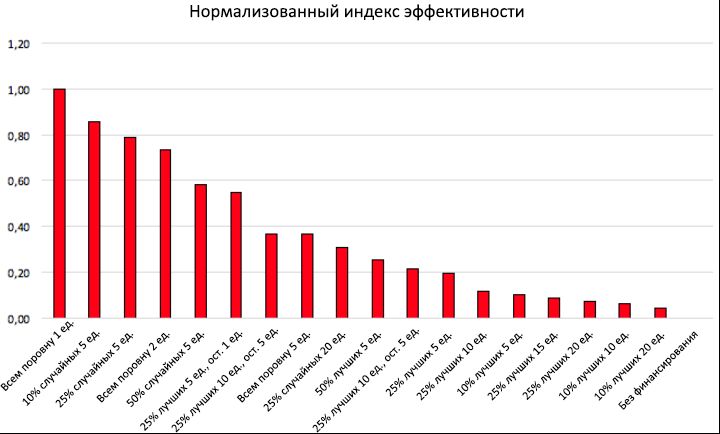
11: .
E norm . , ,
C end >
C (0), , , .
, , «» , 1 5 , ,
E norm = 1 (..,
E =
E max ):
F T 8000 , , « »,
P T0 = 32,05%
P T = 69,48%,
P * T = 37,43. (, 2 5 ), ( 69,48% 94,40%), ,
E norm = 1
E norm = 0,74,
E norm = 0,37, .
, «» , 5 (5, 10, 15 20 ) 50%, 25% 10% , ,
E norm < 0,25 ,
P * T , « », ( 20%), , . , , , .
, «» , .. «» , , 25%, , , « » , . , «» . , , : 16000 ,
P T , , , (70,83% 84,02%),
E norm (0,55 0,74).
( ), . , , , , : , , .
, , . , , , 5 10% , 4000 ,
P * T = 17,78%, . , 25% ( 10000 )
P * T = 35,95, , , . ,
P * T (
P * T = 9,03%), (. 12 ), (10000 ) (25% ). , , , , , , « » , . , , , , [48, 49, 50, 51, 52, 53, 54, 55], , , .
, 12 . , 100
F T = 80000, 5
F T /8 = 10000 , , , . , , ,
P T 100%. ( 50% ), , 25% , , , . , , « » .
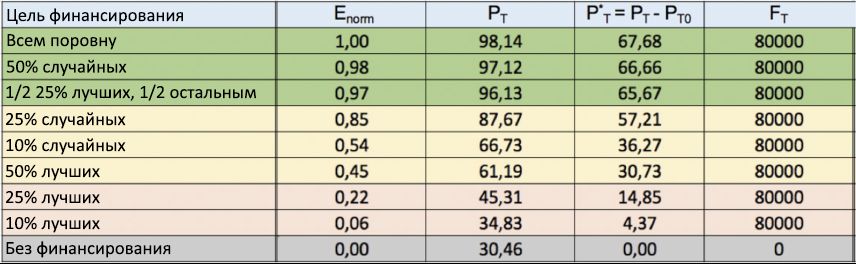
12: .
E norm (1- ) , . 10,
F T = 80000. .
, , (, , ) , . , , , , .
3.2。
, . . , , , , ,
m T ,
σ T , , , , .
13 / , 100 , . , 2.2 (
N = 1000,
I = 80,
δ t = 6,
C (0) = 10,
N E = 500
p L = 50%), . , (a)
m T = 0,6,
σ T = 0,2, (b) ,
σ T = 0,1
m T = 0,7. , .
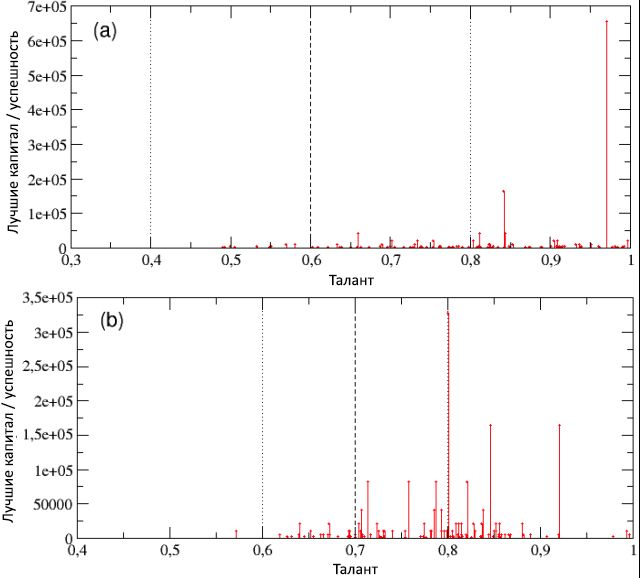
13: 100 , : (a)
m T = 0,6
σ T = 0,2 ( ); (b)
m T = 0,7
σ T = 0,1 ( ).
m T m T ± σ T , , .
, ,
σ T ,
m T , (a), – ,
T = 0,97, /
C best = 655360. , , , , , , , . (b) ,
m T σ T C best = 327680
T = 0,8, ,
C = 163840 , ,
T = 0,85
T = 0,92. , , .
, / 100
C mt ≈ 63, 2.2. ,
C mt ≈ 319 (a)
C mt ≈ 122 (b), . , –
P T , , ..
T >
m T + σ T /
C end > 10,
T >
m T + σ T ( , , ,
m T + σ T = 0,8). ,
P T = 38% (a)
P T = 37,5% (b),
P T0 = 32% (
m T = 0,6
σ T = 0,1).
, , , , , , . , , , , . , , , .
, , , , , .. , - , , .
14 , , , , 100 , , 2.2 (
N = 1000,
m T = 0,6,
σ T = 0,1, I = 80,
C (0) = 10,
N E = 500)
p L (, 2.2
p L = 50%). (a)
p L = 80%, , , [26]. , (b)
p L = 20% , , , , « ».
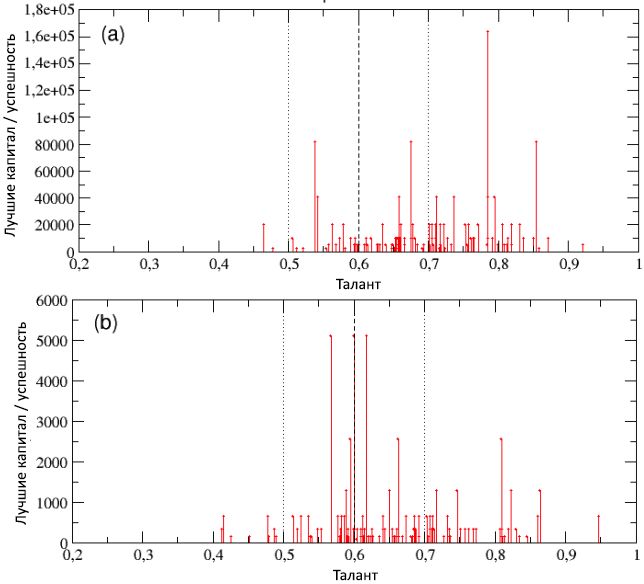
14: 100 ,
p L : (a)
p L = 80%; (b)
p L = 20%. , ,
m T = 0,6
m T ± σ T ,
σ T = 0,1.
, / , ,
p L .
p L = 80%, (a), - ,
p L = 50%, ,
C best = 163840. , / ,
C mt ≈ 149, , ,
P T = 62,18% (
P T0 = 32%), , , , .
p L = 20%. , (b), , , 2.2,
C best 5120 – , . ,
P T , , , 8.75%.
, , , , , , . , , , .
4.
, , , . , , , / , 40 , «80/20», , . , , , – , . . , , / , , . , « », , . , – , . , , , .
, .
- Bak, P., Tang, C. and Wiesenfeld, K., Self-organized criticality. Phys. Rev. A , 38:364{374 (1988).
- Barab´asi, A.-L., Albert, R., Emergence of Scaling in Random Networks, Science , Vol. 286, Issue 5439, pp. 509{512 (1999).
- Newman, MEJ, Power laws, Pareto distributions and Zipf's law, Contemporary Physics , 46 (5): 323{351 (2005).
- Tsallis, C., Introduction to Nonextensive Statistical Mechanics. Approaching a Complex World , Springer (2009).
- Pareto, V., Cours d'Economique Politique , vol. 2 (1897).
- Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
- Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
- Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
- Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
- Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
- Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
- Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
- Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
- Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
- Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
- During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
- During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
- Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
- Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
- Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
- Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
- Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
- Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
- Silberzahn, R., Uhlmann, EL, It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
- Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal , DOI10.2139/ssrn.1348280 (2009).
- Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452{60.
- Du, Q., Gao, H., Levi, MD, The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
- Deaner, RO, Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
- Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House , 424 pp. (2011).
- Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
- Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
- Newgreen, DF et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
- Snyder, RE and Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
- Snyder, RE and Ellner, SP, Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
- .., . , , (2018).
- .., . , (2018).
- Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
- .., . , (2019).
- Watts, DJ, Everything Is Obvious: Once You Know the Answer , Crown Business (2011).
- Salganik, MJ, Dodds PS, Watts DJ, Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
- Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
- Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
- Sinha, S. and Pan, RK, How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds BK Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
- Fortin, J.-M., Curr, DJ, Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
- Jacob, BA, Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
- O'Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
- Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences , 109(24):9331{9336 (2012).
- Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
- Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
- Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
- Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
- Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
- Biondo, AE, Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
- Biondo, AE, Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
- Biondo, AE, Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
- Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
- Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
- . ., , II: , https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
- Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences , DOI: 10.1073/pnas.1719557115 (2018).
- Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
- Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
- Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
- Benias, PC et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports , vol. 8, 4947 (2018).
- Flexner, A, The Usefulness of Useless Knowledge , Princeton University Press, Princeton (2017).
- Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence. , Nature Editorial, Vol.554, 1 February 2018.
- Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
- Page, SE, The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
- Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
- Curry, S., Let's move beyond the rhetoric: it's time to change how we judge research, Nature 554, 147 (2018).
- Nicholson, JM and Ioannidis, JPA, Research grants: Conform and be funded, Nature 492, 34{36 (2012).
- Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
- Garner, HR, McIver, LJ and Waitzkin, MB, Research funding: Same work, twice the money?, Nature 493,599{601 (2013).
: Talent vs Luck: the role of randomness in success and failure