G.M.工作的插图 Adelson-Welsky和E.M. 兰迪斯1962
搜索树是用于有序存储和简单搜索项目的数据结构。 二进制搜索树被广泛使用,其中每个节点只有两个孩子。 在本文中,我们考虑了两种组织二叉搜索树的方法:Adelson-Welsky和Landis算法(AVL树)和弱化AVL树(WAVL树)。
让我们从定义开始。 二进制树由节点组成,每个节点以键-值对的形式(或在简单情况下,仅值)形式存储一条记录 ,并且最多有两个子级 。 后代节点通过左右区分,并且满足密钥排序的条件:左子节点的密钥不再多,右子节点的密钥不小于父节点的密钥。 另外,服务信息可以存储在(并且通常存储在)节点中,例如,到父节点的链接或其他数据。 特殊情况是树进入的根节点 ,以及不存储任何信息的空节点 。 两个后代都为空的节点称为树叶 。 具有所有后代的节点形成一个子树 。 因此,每个节点都是子树的根或叶。
此定义使您可以构建用于存储节点和树本身的简单结构。 我们假定一个空节点的特殊值为Nothing类型。 然后,在节点中存储对右后代和左后代以及对父代的引用就足够了。 用于存储树的结构仅包含指向根节点的链接。
在这种情况下,出现了如何表示一棵空树的问题。 为此,我们使用《算法:构造和分析》一书中的方法,将不是根的而是作为其父节点的虚拟节点作为入口插入到树中。 要创建这样的节点,请将构造函数添加到BSTNode结构描述中:
mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V}
在这种情况下,可以使BST结构保持不变,因为 链接到入口点的链接将不再需要更改。 此外,我们假设树的根节点紧接输入节点的左右后代。
自然,需要搜索树的主要操作是搜索元素。 由于左子键不多,右子键不小于父键,因此元素搜索过程的编写非常简单:从树的根开始,将输入键与当前节点的键进行比较; 如果键匹配,则返回值;否则,根据键的顺序转到左或右子树。 如果它们同时到达一个空节点-树中没有键,则引发异常。
通过键搜索元素显然需要O ( h )时间,其中h是树的高度,即 从根到叶的最大距离。 可以很容易地计算出一个高度为h的二叉树如果人口稠密 ,最多可以包含2 h +1 1 -1个节点。 除了非常极端的一层之外,所有节点都具有两个后代。 另外,很明显,任何预先给定的键序列都可以导致这种密集的树。 这给出了一种在树中搜索元素的非常乐观的渐近行为,其时间为O (log 2 N ),其中N是元素的数量。
自然地,需要以一种满足键顺序的条件的方式来构造用于将元素添加到搜索树的算法。 让我们编写一个通过键插入元素的简单实现:
不幸的是,树的幼稚构造只能在随机输入数据上给出所需的结构,但实际上它们通常是相当结构化的。 在最坏的情况下,如果严格要求输入密钥的顺序(至少按升序,至少按降序排列),则幼稚树结构将始终在一个方向上发送新元素,实际上是收集线性列表。 很容易猜测元素的插入,即搜索将在O ( N )期间以这种结构进行,这否定了构建复杂数据结构的所有努力。
结论:搜索树必须在构建过程中保持平衡 ,即 在每个节点处对齐左右子树的高度。 有几种平衡方法。 最简单的是指定一定数量的插入或删除操作,此后将重新平衡树。 在这种情况下,树在平衡之前将处于相当“运行”的状态,因为在最坏的情况下,平衡将花费大约O ( N )时间,但是后续操作将达到对数时间,直到达到插入/删除的特定阈值。 另一个选择是立即构建插入和删除算法,以使树始终保持平衡,这为任何操作提供了保证的时间复杂度O (log 2 N )。
由于存在允许树``狂野''的算法,但是在那之后,可以在对数时间内在相当长的时间内执行操作,然后必须将树长时间恢复到平衡状态,才能区分元素插入/删除的保证和摊销时间。 对于使用二分搜索树的操作的某些实现,可以保证插入和删除O (log 2 N )的复杂性,对于某些算法则可以分摊,从而降低O ( N )。
Adelson-Welsky和Landis算法(AVL)
自平衡二进制搜索树的第一个实现是1962年由Adelson-Welsky和Landis提出的。 在现代文学中,关于姓氏首字母的这种结构称为AVL树 。 该结构由以下属性描述:
- 顺序:对于任何节点,左子树顶部的键小于右子树顶部的键(如果后代不是空节点)。
- 高度增加:父节点的高度比其后代的最大高度大一。 空节点的高度可以认为等于零。
- AVL平衡:对于任何节点,左右子树的高度相差不超过1。
从这些属性可以得出,整棵树的高度是O (log 2 N ),其中N是存储在树中的记录数,这意味着该记录是在对数时间内搜索的。 为了在每次插入之后保持ABL平衡的状态,每次插入都需要进行平衡操作。 为了有效地执行此操作,每个节点都需要存储服务信息。 为简单起见,只需将节点的高度保持在那里。
mutable struct AVLNode{K,V}
插入记录
基本插入是根据标准算法完成的-向下浏览树,寻找可以插入新节点并插入的位置。 我们将编写包装器,以使用索引-1和1而不是左右索引来获取和替换子节点:
function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end
接下来,我们走到树上,查找是否违反条件2和3。接下来,我们考虑可能出现的选项(在图中,绿色表示更改高度的节点,正在处理的节点为其父节点)。
案例0
插入后,节点的高度与姐妹节点的高度相同,比父节点的(旧)高度小1。
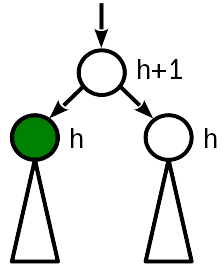
最好的情况是,无需进一步接触。 上方,您也无法观看,因为 那里什么都不会改变。
情况一
在插入之前,结的高度等于姐妹结的高度。 插入将提升子树的根,并将节点的高度与父节点的高度进行比较。
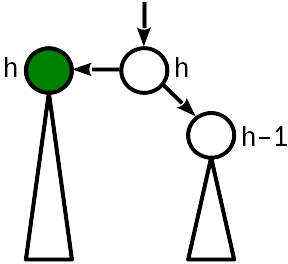
在这种情况下,足以“提升”父节点,将其高度增加1。同时,您需要继续移至树的根,因为更改父节点的高度可能会导致违反条件2一级。
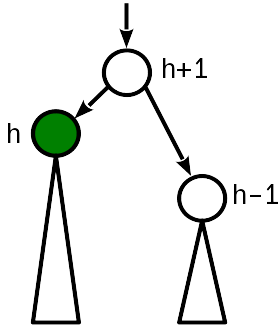
代号 fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end
情况二
插入后,与子树的高度差变为2,而左子树“推”向上:
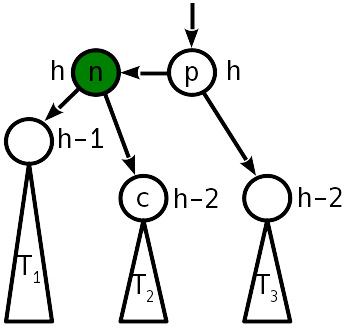
可通过称为“简单旋转”的操作来解决该问题,该操作将树转换如下:
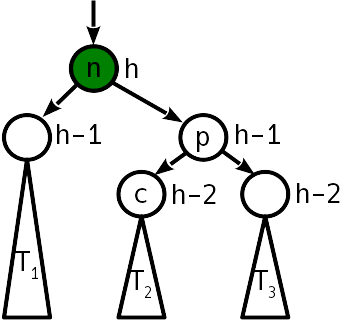
一个简单的转弯就需要更改6个指针。
注意,在水平轴上的投影中,旋转前后的顶点n , p和树T 1 - T 3的顺序保持不变。 这是订购条件的满足。 如您所见,打开树后,不再需要平衡。
情况3
插入后,与子树的高度差变为2,右子树“推”上:
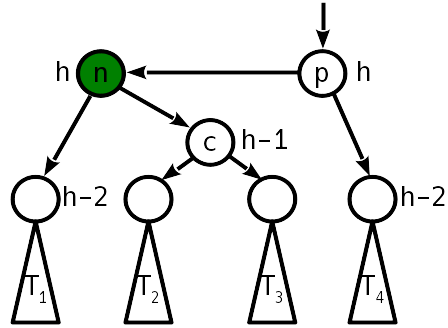
在这种情况下,一个简单的转弯将不再有用,但是您可以绕着右后代进行简单的左转,这将导致情况2,该情况已经通过简单的向右转进行了处理。
为了减少节点的“重量”数,可以将两匝合并为一个操作,称为大匝或双匝。 然后,无需更改12个指针,只需10个指针即可。由于两次旋转,该树采用以下形式:
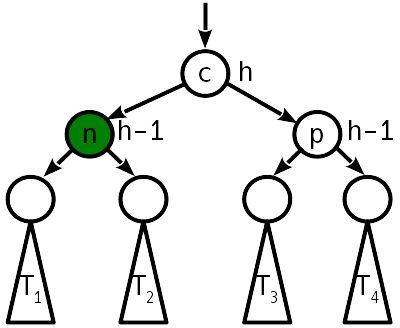
如您所见,在两次转弯之后,也不需要进一步平衡树。
因此,在将记录插入AVL树中时,需要在有关节点高度的信息中进行O (log 2 N )个更改,并且最多进行两次旋转操作。 将所有内容组合到一个插入函数中。 它与基本插入的区别仅在于,在插入新节点之后,将fix_insertion!()函数,该函数将从新插入的节点传递到根,检查并在必要时更正余额。
function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left
fix_insertion!()函数从插入的父节点开始检查两个子节点之间的高度差。 如果它等于1-在情况1中,则需要提高节点的高度并向更高方向移动。 如果为零,则树是平衡的。 如果等于2-这是情况2或3,则需要应用适当的旋转,树将达到平衡状态。
删除记录
移除比插入困难。
首先,考虑从二叉搜索树中通常删除条目。
- 如果已删除的记录在工作表中,那么该记录将被简单地删除,此处的一切都很简单。
- 如果已删除的记录位于只有一个后代的节点中,则该后代及其所有子树都将放置在远程节点的位置。
- 如果有两个后代,则从树中提取最大子元素,或从左侧子树中搜索最小子元素(通过搜索树的属性,保证最大元素的节点不具有右后代,但最小子节点不向左,因此此删除很容易)代替已删除的记录。
但是在那之后,树平衡可能会受到干扰,因此您需要从远程节点的父节点上来,进行恢复。 请注意,一开始就要确保所讨论的父级的后代之一将高度降低1。考虑到这一点,您需要考虑以下选项(更改高度的节点以红色显示,处理后的节点是红色的父级):
情况一
零失衡。 因此,在删除之前,它是1模,现在子节点比父节点低2。
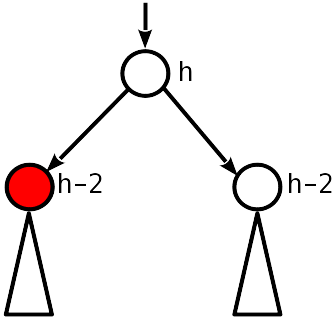
您需要将父节点降低1并继续向上移动。
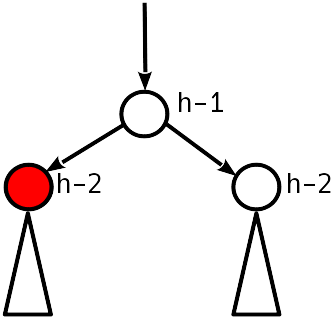
情况二
不平衡1模。
AVL条件已满足,您可以停止。
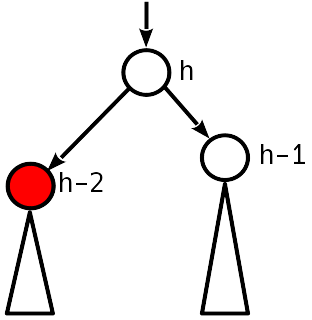
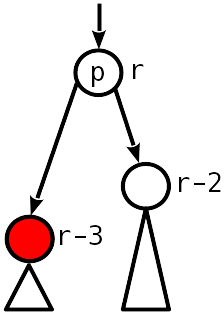
情况3
不平衡2是模数,降序的姊妹节点具有不为零的不平衡。
我们可以通过简单的操作(如果T 1低于T 2 )或通过两次(否则)旋转来恢复平衡,就像在插入过程中那样。 子树的高度减小,即 在树上方可能会发生违规。
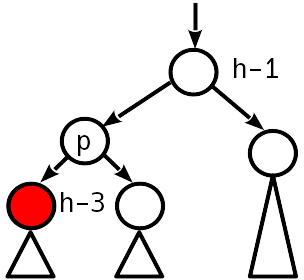
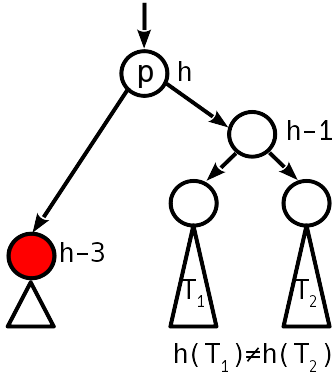
案例4
不平衡2为模,姊妹节点不平衡为零。
简单旋转即可恢复平衡条件,而子树的高度不会改变-我们停止向上移动。
钥匙取出码 function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end
AVL树的兴衰
经典AVL树的一个不太好的功能是删除记录的困难: 旋转可以将整个子树向下“重置”一级,然后在最坏的情况下,删除操作需要O (log 2 N )树旋转-每次您在fix_deletion!()中上fix_deletion!()一级。
由于这种不太好的渐近行为,AVL树被1970年代出现的红黑树所取代,并且平衡条件较弱-从根到最远的叶子的路径不超过从根到最近的叶子的路径的两倍。 因此,在最坏的情况下,红黑树的高度为2log 2 N ,而AVL树的高度为1.44log 2 N ,但是删除一条记录最多需要进行三个简单的旋转。 因此,由于较高的树高而导致的搜索和插入可能会降低性能,但是如果插入时常插入删除点,则会有潜在的收益。
AVL反击
事实证明,在添加或删除记录时,用于构建二分搜索树的“理想”算法应保证较小的高度(在经典AVL树的水平上)和固定的旋转数。 这尚未被发明,但在2015年发表了一项工作 ,提出了一种可以改善AVL和红黑树特性的结构。 这个想法更接近AVL树,但是放宽了平衡条件以允许更有效地删除记录。 称为“弱AVL树”(W(eak)AVL树)的结构的属性公式如下:
- 顺序:对于任何节点,左子树顶部的键小于右子树顶部的键(如果后代不是空节点)。
- 升序。 每个节点被分配一个等级。 所有空节点的等级为零,图纸的等级为1。父节点的等级严格大于子节点的等级。
- ABL平衡不足:节点的等级与子节点的等级相差不超过2。
事实证明,这种结构既包括经典AVL树又包括红黑树的属性。 特别是,如果引入两个子节点的等级不能与父节点的等级相差2的条件,我们将得到一个规则的AVL树,并且等级将与子树的高度完全匹配。
SAVL树的优点在于,略微减弱AVL条件可使删除记录的记录树平衡不超过两圈! 树高估计为h <min(1.44log 2 M ,2log 2 N ),其中N是树中的条目数, M是插入数,而红黑树的h <2log 2N 。 , - , , .
- , . - .
.
-, "" "". , :
mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V}
, -. : 1 , — , 0 ( ) 1 ( ). imbalance() , , .
wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end
, . , , , , -, - .
, — -. .
0
, ..:
- 1, 1
- 0, 2 , .
.
1
2 ( 0, 2 ).
1 .
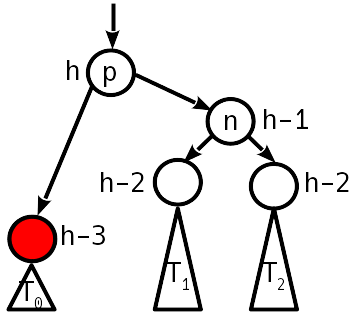
2
1, 2.
1, .
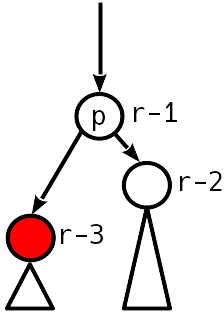
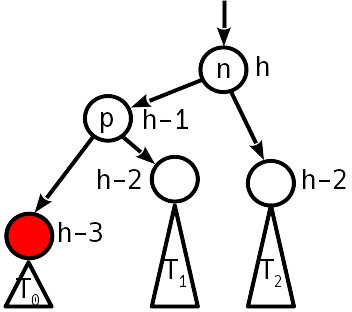
3
2 ( 1, .. ), 2 .
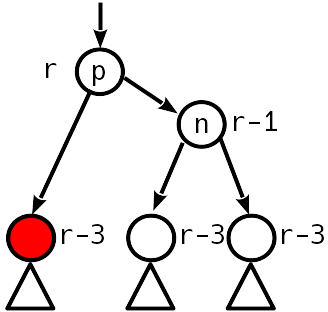
, . .
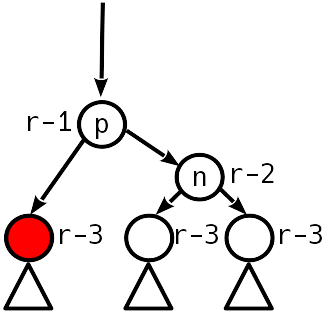
4
.
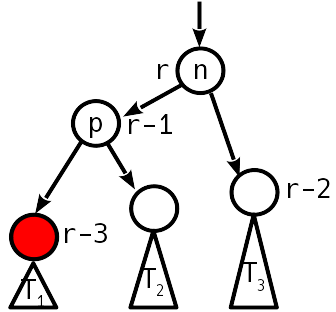
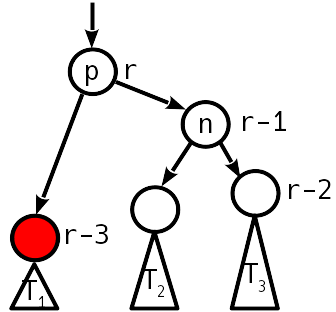
, , , .. .
— T 1 T 2 , p 2, p 1.
5
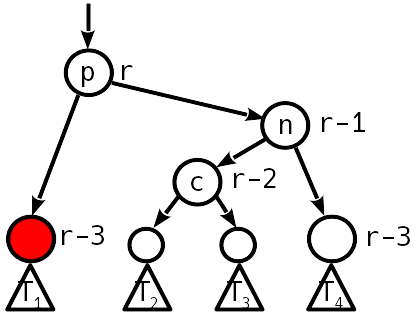
.
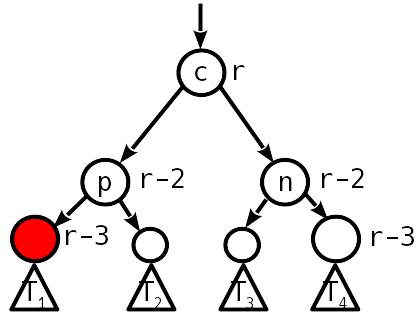
, , .
function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end
-.
julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000)
, , . , , - , -, .
— ?
— , . , , .
.
— , . n - . , , .. , .
*
— , " ", " ", " -", " ". , , -. . , .
*
** O (1), ...
, " — ". , . — ( ) , , , . .
*
** ,
结论
() — , , , , , . — , .. , , .
参考文献
- "-" nickme
- Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
- Goodrich MT, Tamassia R. Algorithm Design and Applications