在硕士专业“通信与信号处理”(TU Ilmenau)中开发摘要主题时,我想继续学习“自适应与阵列信号处理”课程的主要主题之一。 即,自适应滤波的基础。
本文最初是为谁编写的:
1)对于本地专业的学生团体;
2)对于准备实践研讨会但尚未决定工具的老师-以下是python和Matlab / Octave中的示例;
3)对于任何对过滤主题感兴趣的人。
可以在切割下找到什么:
1)来自理论的信息,我试图尽可能简洁地进行整理,但在我看来,这是翔实的;
2)滤波器使用示例:特别是作为天线阵列均衡器的一部分;
3)链接到基本文献和开放库(使用python),这可能对研究有用。
一般来说,欢迎您,让我们按要点对所有内容进行排序。

我想,照片中沉思的人对许多人来说都是Norbert Wiener所熟悉的。 在大多数情况下,我们将研究他的名字的过滤条件。 但是,不能不提及我们的同胞安德烈·尼古拉耶维奇·科尔莫戈洛夫(Andrei Nikolaevich Kolmogorov),他在1941年的文章也为最优滤波理论的发展做出了重要贡献,即使在英语中也被称为Kolmogorov-Wiener滤波理论 。
我们在考虑什么?
今天,我们正在考虑具有有限冲激响应(FIR,有限冲激响应)的经典滤波器,可以通过以下简单电路来对其进行描述(图1)。
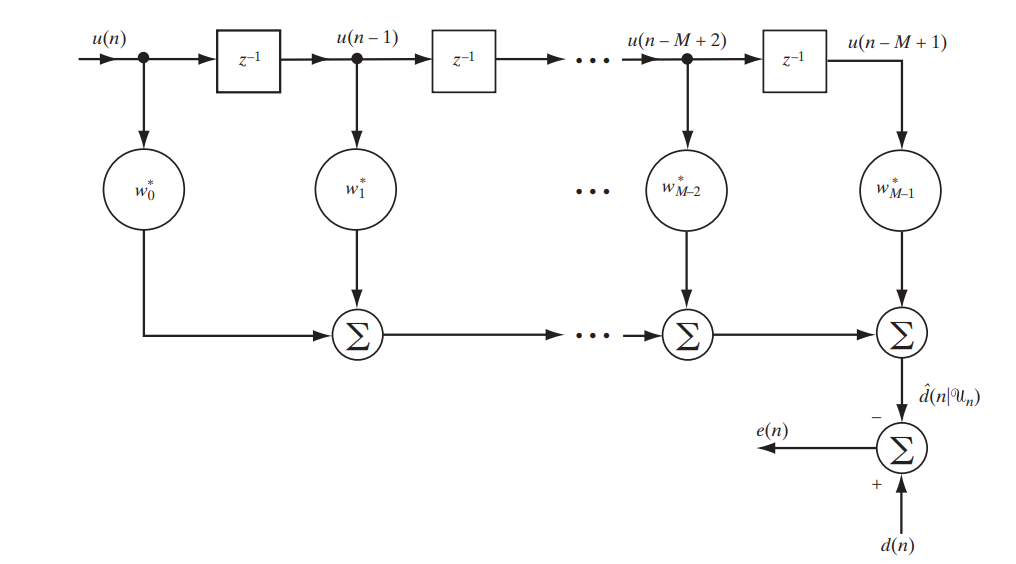
图1。 研究维纳滤波器的FIR滤波器方案[1。 第117页]
我们将以矩阵形式编写此展位输出的确切信息:
解密符号:
 给定和接收信号之间的差异(误差)是
给定和接收信号之间的差异(误差)是 是一些预定义的信号
是一些预定义的信号 是样本的向量,或者换句话说,是滤波器输入端的信号
是样本的向量,或者换句话说,是滤波器输入端的信号 信号在滤波器输出端吗
信号在滤波器输出端吗 -这是滤波器系数向量的Hermitian共轭-滤波器的适应性在于它们的最佳选择
-这是滤波器系数向量的Hermitian共轭-滤波器的适应性在于它们的最佳选择
您可能已经猜到了,我们将努力在给定信号和滤波信号之间寻求最小的差异,即最小的误差。 这意味着我们正面临优化任务。
我们将优化什么?
为了优化或最小化,我们不仅会表示误差, 均方误差 ( MSE-均方误差 ):
在哪里  表示滤波器系数向量的代价函数,并且
表示滤波器系数向量的代价函数,并且  表示垫子。 等待中。
表示垫子。 等待中。
这种情况下的平方非常令人愉快,因为这意味着我们面临着凸编程的问题(我只用谷歌英语凸优化的类似物),这反过来意味着一个极值 (在我们的例子中是最小)。
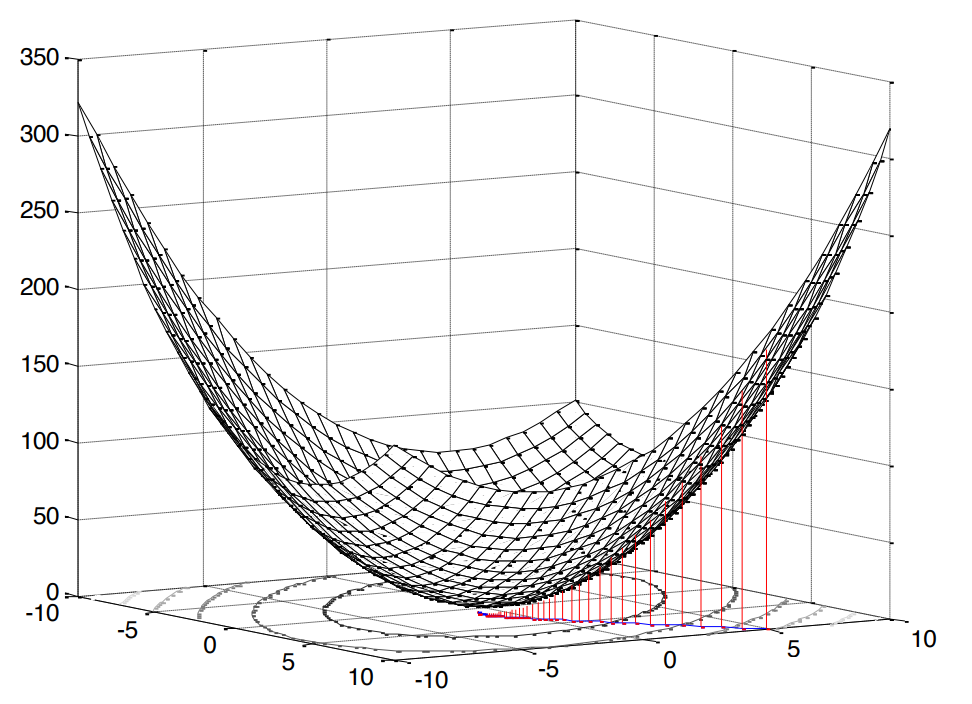
图2。 表面的均方误差 。
我们的误差函数具有规范形式[1,第121页]:
在哪里  是预期信号的方差,
是预期信号的方差,  是输入矢量和期望信号之间的互相关矢量,并且
是输入矢量和期望信号之间的互相关矢量,并且  是输入信号的自相关矩阵。
是输入信号的自相关矩阵。
如上所述,如果我们谈论凸编程,那么我们将有一个极值(最小)。 因此,要找到成本函数的最小值(最小均方根误差),找到切线斜率的切线就足够了,换句话说, 就我们的研究变量而言 ,找到偏导数就足够了:
在最佳情况下(  ),误差当然应该很小,这意味着我们将导数等于零:
),误差当然应该很小,这意味着我们将导数等于零:
实际上,这里是我们的炉子,从中我们可以进一步跳动:在我们前面的是一个线性方程组 。
我们将如何决定?
应当立即指出,在这种情况下,我们将在下面讨论的两种解决方案都是理论上和教育上的,因为  和
和  事先已知(也就是说,我们据称有能力收集足够的统计数据来进行计算)。 但是,这里对此类简化示例的分析是理解基本方法的最佳方式。
事先已知(也就是说,我们据称有能力收集足够的统计数据来进行计算)。 但是,这里对此类简化示例的分析是理解基本方法的最佳方式。
分析溶液
可以说,可以使用反矩阵在额头上解决此问题:
这样的表达式称为维纳-霍普夫方程-它仍然对我们有用。
当然,要完全谨慎,以一般的方式记下这种情况可能更正确,即 不与  和
和  ( 伪反转 ):
( 伪反转 ):

但是,自相关矩阵不能是非平方或奇异的,因此,很正确地,我们认为不存在矛盾。
从该方程式可以分析得出成本函数的最小值等于多少(即在我们的情况下MMSE-最小均方误差):
好吧,有一种解决方案。
迭代解
但是,是的,可以解决线性方程组而无需反演自相关矩阵的情况( 以节省计算量 )。 为此,请考虑使用本机且易于理解的梯度下降 方法(最陡/梯度下降方法 )。
该算法的实质可以简化为以下几点:
- 我们将所需变量设置为某个默认值(例如,
 )
) - 选择一些步骤
 (我们如何选择,我们将在下面讨论)。
(我们如何选择,我们将在下面讨论)。 - 然后,实际上,我们沿着给定的步骤沿着原始曲面(在本例中,这是MSE曲面)下降
 并由梯度的大小确定一定的速度。
并由梯度的大小确定一定的速度。
因此,名称为: 梯度 -梯度或最陡 -逐步下降 -下降。
在我们的案例中,梯度是已知的:实际上,是在微分成本函数时发现的(表面为凹面,与[1,p。220]比较)。 我们写了所需变量(滤波器系数)的迭代更新公式如何看起来像[1,p。 220]:
在哪里  是迭代次数。
是迭代次数。
现在让我们谈谈选择步长的方法。
我们列出了明显的前提:
- 步骤不能为负或零
- 步长不应太大,否则算法将不会收敛(实际上,它会从一条边跳到另一边,而不会陷入极端)
- 当然,步长可能很小,但这也不是完全理想的-算法将花费更多时间
关于维纳过滤器,当然,很早以前就已经发现了限制条件[1,第222-226页]:
在哪里  是自相关矩阵的最大特征值
是自相关矩阵的最大特征值  。
。
顺便说一下,在线性滤波的背景下,特征值和向量是一个单独的有趣主题。 在这种情况下,甚至有一个完整的本征滤波器 (请参阅附录1)。
幸运的是,这还不是全部。 还有一个最佳的自适应解决方案:
在哪里  是负梯度。 从公式中可以看出,该步骤将重新计算到每次迭代中,也就是说,它可以适应。
是负梯度。 从公式中可以看出,该步骤将重新计算到每次迭代中,也就是说,它可以适应。
公式的结论在这里(很多数学-只看像我这样臭名昭著的书呆子)。 好的,对于第二个决定,我们也做好了准备。
但是有可能举例吗?
为了清楚起见,我们将进行一个小的模拟。 我们将使用Python 3.6.4 。
我将立即说这些示例是一项家庭作业的一部分,每项作业将在两周内提供给学生以解决。 我在python下重写了该部分(以便在无线电工程师中普及该语言)。 也许您会在网上找到其他以前的学生的其他选择。
import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]
我们将使用线性滤波器解决信道均衡问题,其主要目的是均衡该信道对有用信号的各种影响。
可以在此处或此处的一个文件中下载源代码(是的,我有这样的爱好-编辑Wikipedia)。
系统型号
假设有一个天线阵列(我们已经在有关MUSIC的文章中对其进行了检查)。
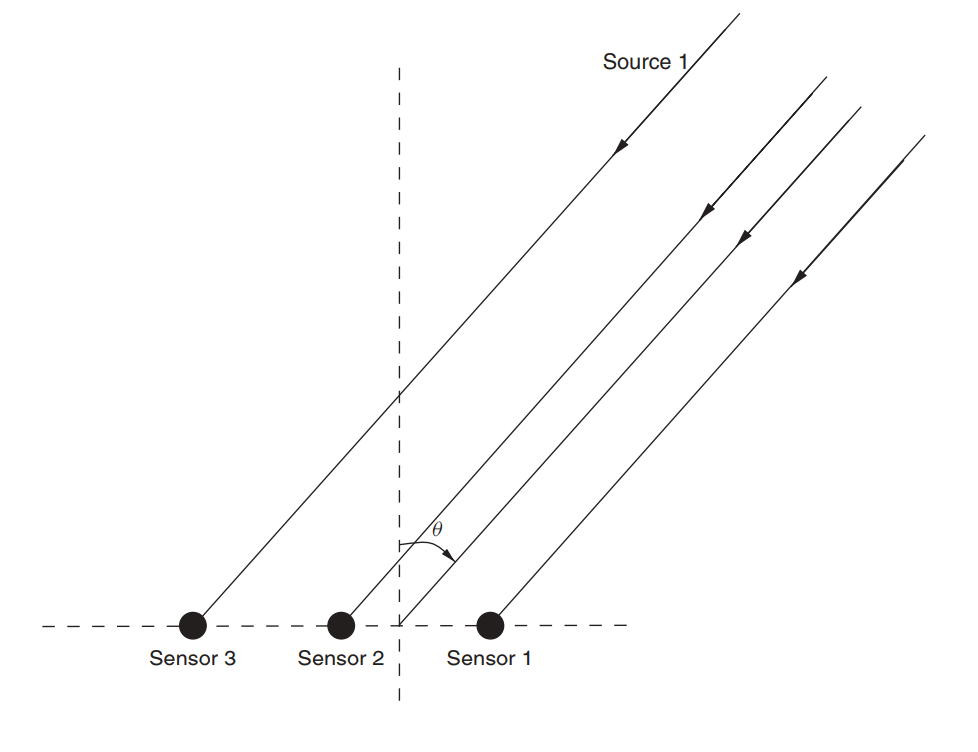
图 3.无方向性线性天线阵列(ULAA-均匀线性天线阵列)[2,p。 32]。
定义初始晶格参数:
M = 5
在本文中,我们将考虑带有衰落的宽带信道之类的东西,其特征是多径传播 。 对于这种情况,通常采用一种方法,其中使用一定幅度的延迟对每个波束建模(图4)。
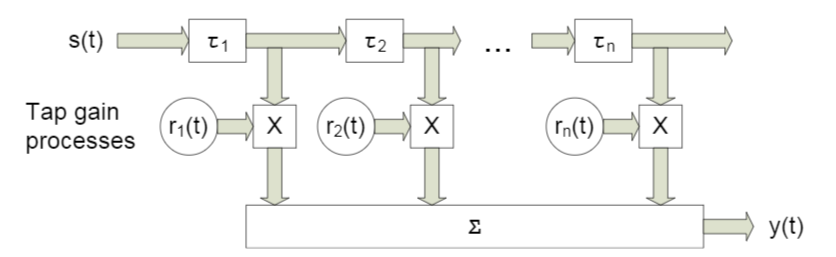
图 4.具有n个固定延迟的宽带信道模型[3,p。2]。 29]。 如您所知,特定名称不起作用-在接下来的内容中,我们将使用略有不同的名称。
一个传感器的接收信号模型表示如下:
在这种情况下  表示参考编号,
表示参考编号,  是信道沿着第l束的响应, L是延迟寄存器的数量, s是传输的(有用的)信号,
是信道沿着第l束的响应, L是延迟寄存器的数量, s是传输的(有用的)信号,  -加性噪声。
-加性噪声。
对于多个传感器,公式将采用以下形式:
在哪里  和
和  -有尺寸
-有尺寸  尺寸
尺寸  等于
等于  ,以及尺寸
,以及尺寸  等于
等于  。
。
假设由于波以一定角度入射,每个传感器还接收到具有一定延迟的信号。 矩阵  在我们的例子中,它将是每条射线的响应向量的卷积矩阵。 我认为代码会更清晰:
在我们的例子中,它将是每条射线的响应向量的卷积矩阵。 我认为代码会更清晰:
h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1
结论将是:
>>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])
接下来,我们为有用的信号和噪声设置初始数据:
sigmaS = 1
现在我们转到相关性。
Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))
我们找到了维纳的解决方案:
现在,让我们继续进行梯度下降法。
找到最大特征值,以便可以从中推导台阶的上边界(参见公式(9)):
lamda_max = max(np.linalg.eigvals(Rxx))
现在,让我们设置一些步骤,这些步骤将构成最大值的一部分:
coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff
定义最大迭代次数:
N_steps = 100
运行算法:
MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)
现在,我们将执行相同的操作,但对于自适应步骤(公式(10)):
MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)
您应该得到这样的内容:
画图 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()
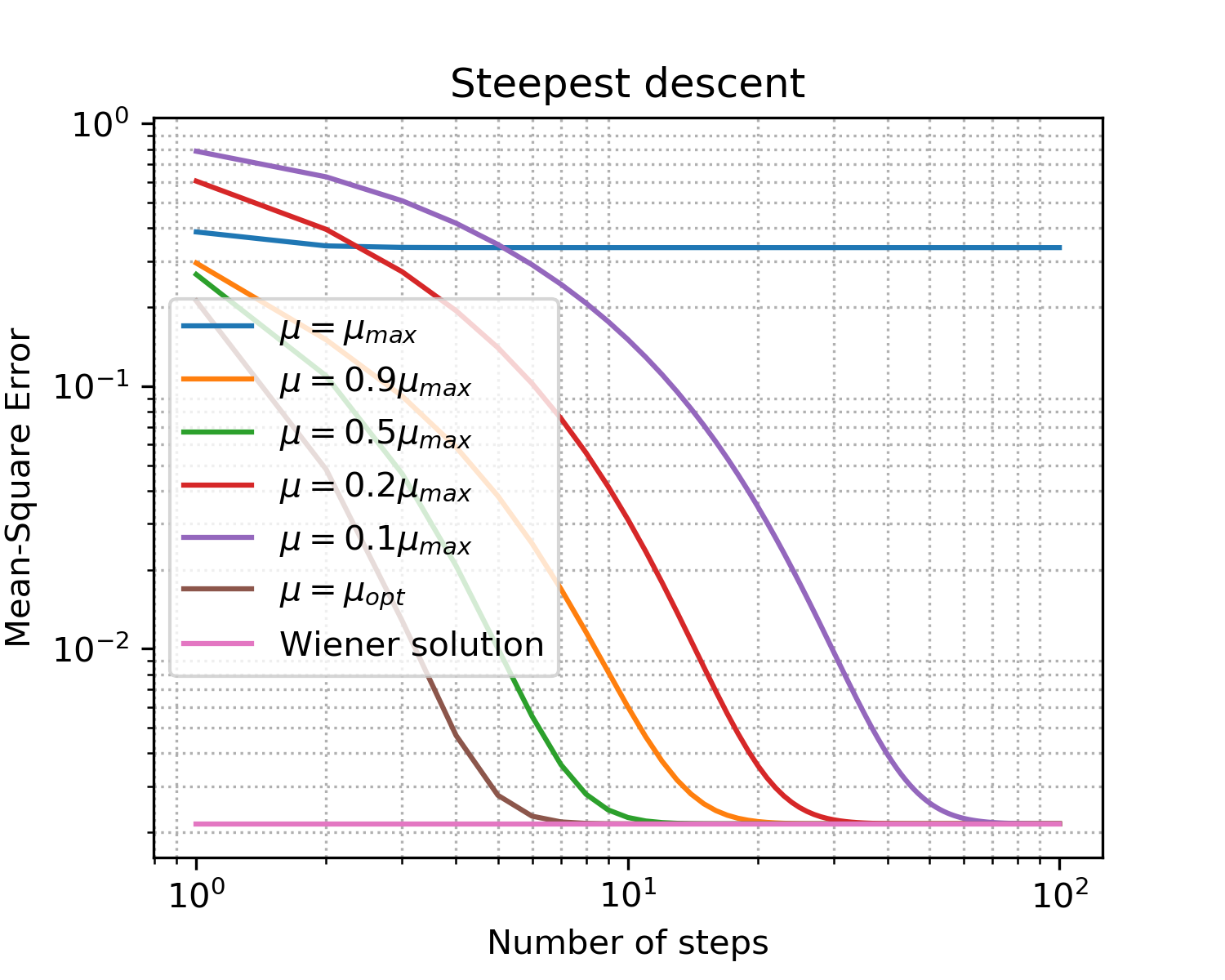
图 5.学习不同大小步长的曲线。
为了说明有关梯度下降的要点,紧固件:
- 不出所料,最佳步骤可提供最快的收敛速度;
- 不再意味着更好:超出上限之后,我们根本没有达到收敛。
因此,我们找到了滤波器系数的最佳矢量,它可以最佳地平化通道的效果-我们训练了均衡器 。
有没有更接近现实的东西?
当然可以! 我们已经说过好几次了,在实时系统中收集统计数据(即计算相关矩阵和向量)远非总是负担得起的。 但是,人类已经适应了这些困难:在实践中,不是采用确定性方法,而是使用了自适应方法。 它们可以分为两个大组[1,p。1。 246]:
自适应过滤器的主题在开源社区(python示例)中得到了很好的体现:
在第二个示例中,我特别喜欢该文档。 但是,要小心! 当我测试padasip软件包时,在处理复数时遇到了困难(默认情况下,float64隐含在其中)。 当使用某些其他实现时,可能会出现相同的问题。
当然,算法各有优缺点,其总和决定了算法的范围。
让我们快速看一下示例:我们将考虑已经提到的三种算法SG , LMS和RLS (我们将以MATLAB语言进行建模-我承认,已经存在空白,为了...而将所有内容重写为均一Python)。
LMS和RLS算法的说明可以在例如padasip扩展坞中找到。
1)与上述情况类似的情况。
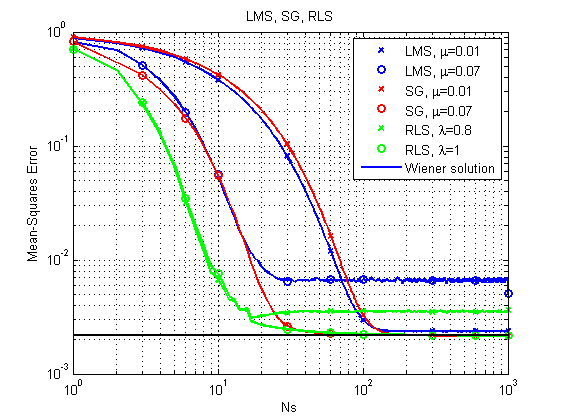
图 6. LMS,RLS和SG的学习曲线。
可以立即注意到,由于LMS算法相对简单,原则上可能不会以较大步长获得最佳解决方案。 RLS给出最快的结果,但是它也可能由于相对较小的遗忘因子而失败。 到目前为止,SG表现不错,但让我们来看另一个示例。
2)频道随时间变化的情况。
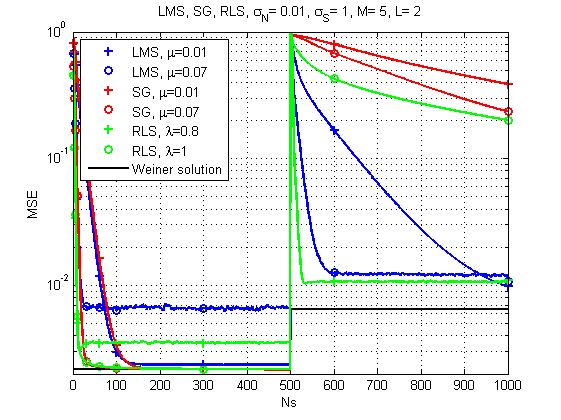
图 7.学习LMS,RLS和SG的曲线(通道随时间变化)。
而这里的情况已经变得更加有趣:随着信道响应的急剧变化,LMS已经似乎是最可靠的解决方案。 谁会想到的。 尽管具有正确遗忘因子的RLS也可以提供可接受的结果。
关于性能的几句话。是的,当然每种算法都有其特定的计算复杂度,但是根据我的测量,我的旧机器可以在LMS和SG的情况下每次迭代处理大约120μs的时间,而在RLS的情况下每次迭代处理250 s的时间。 即,通常该差异是可比较的。
今天就这些了。 感谢所有看过的人!
文学作品
- Haykin SS自适应滤波器理论。 -印度Pearson Education,2005年。
- Haykin,Simon和KJ Ray Liu。 阵列处理和传感器网络手册。 卷 63.约翰·威利父子(John Wiley&Sons),2010年。 102-107
- Arndt,D.(2015年)。 陆上移动卫星接收的信道建模(博士学位论文)。
附录1
本征过滤器这种滤波器的主要目的是使信噪比(SNR)最大化。
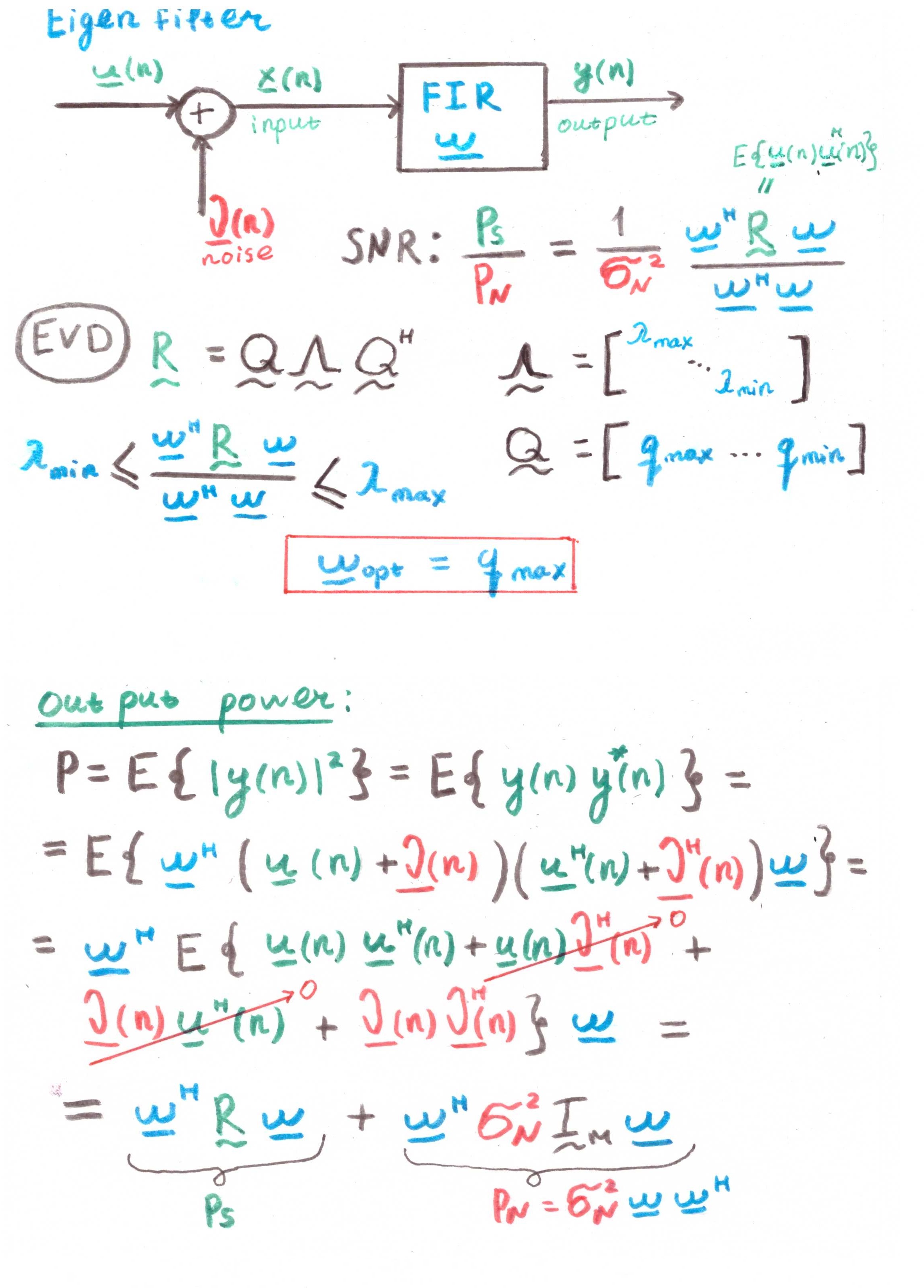
但是从计算中存在相关性来看,这也更多是一种理论构造,而不是实际解决方案。