将细胞自动机与遗传算法联系起来,看看会发生什么。
本文包含Gif(流量!)和对比图像。 癫痫病患者可能会癫痫发作。细胞自动机规则
最简单的元胞自动机是一维元胞自动机(也有零维自动机-我们将在下面讨论它们)。 在一维元胞自动机中,我们有一维数组,其中的元胞(元胞)可以采用两种状态之一(1/0,真/假,白/黑,活/死)。 根据一些规则,阵列中单元的下一个状态由单元的当前状态和两个相邻单元的状态确定。
总计存在
23=8 单元状态和两个相邻单元的组合:

接下来,对于每种组合,我们为下一次迭代(对于自动机的下一个状态)编写单元的状态:
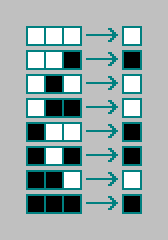
有了细胞自动机的规则。 一维元胞自动机的规则用8位编码(“钨代码”)。 总计存在
28=256 基本细胞自动机:
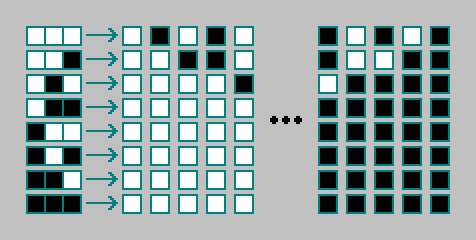
可以手动整理256台机器。 我们将不讨论它们。 我们计算二维元胞自动机的现有规则数量。
二维元胞自动机使用二维数组。 每个单元在Moore附近有8个邻居(还有一个von Neumann邻域,其中不考虑对角单元。在本文中我们将不考虑):

为了方便起见,我们将单元格写在一行中(我们将在本文后面使用选定的顺序):
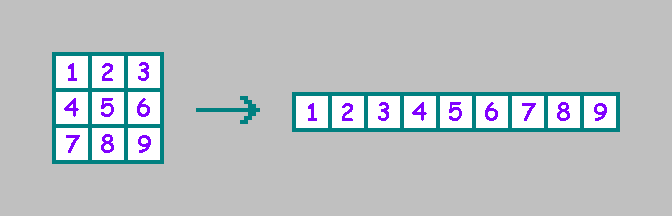
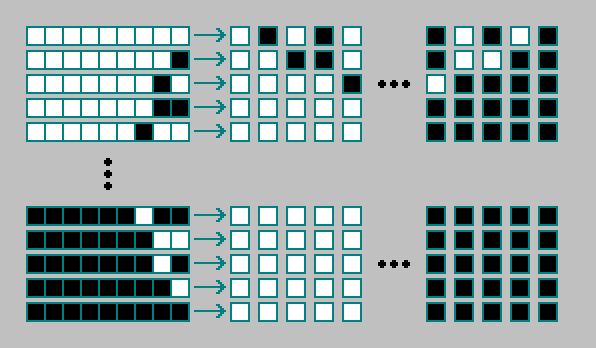
对于二维元胞自动机,存在
29=512 单元状态和8个相邻单元的组合:

二维元胞自动机的规则以512位编码。 总计存在
2512 二维细胞自动机:
号码:
2512\约1.340781 times10154
可观察的宇宙中有更多
原子 (
1080 )
手动无法解决此数量的计算机。 如果我们每秒查看一个自动机-在宇宙存在期间,我们将设法查看所有内容
\约4.35 times1017 自动机。
简单的枚举不起作用,但是借助遗传算法,我们可以找到最适合某些预定义条件的自动机。
我们将使用JavaScript进行编程。 所有代码片段都隐藏在扰流器下,以免使不熟悉编程语言的读者感到困惑。
二维元胞自动机
我们编写带有随机规则的二维元胞自动机。 我们将规则存储在规则数组中,规则数组的长度rulesize = 512:
填写规则数组var rulesize=512; var rule=[]; for(var i=0;i<rulesize;i++) rule[i]=Math.round(Math.random());
接下来,用随机数填充机器的初始状态:
我们填写机器的初始状态 var sizex=89; var sizey=89; var size=2; var a=[]; for(var x=0;x<sizex;x++){ a[x]=[] for(var y=0;y<sizey;y++){ a[x][y]=Math.round(Math.random()); if(a[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } }
(在本文中以及本文的后续部分中,作为机器的宽度和高度,将采用随机数-不是很大,也不是很小的奇数89)计算自动机以下状态的函数如下所示(为了不乱扔垃圾,它删除了画布的初始化):
我们考虑自动机的以下状态 function countpoints(){ var temp=[]; var xm, xp, ym, yp, q; for(var x=0;x<sizex;x++){ xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0; temp[x]=[]; for(var y=0;y<sizey;y++){ ym=y-1; if(ym==-1) ym=sizey-1; yp=y+1; if(yp==sizey) yp=0; q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q]; if(temp[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } } a=temp; }
变量xm和xp在左侧存储邻居的X坐标,在右侧存储邻居的X坐标(x减号和x加号)。 变量ym和yp存储相应的Y坐标。
在这里:
机器的领域被卷成百吉饼 xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0;
我们设置周期性边界条件(自动机的场是圆环的表面)。
下一个:
...进一步 q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q];
按照上述顺序,将单元格的内容写入字符串。 我们将字符串转换为十进制数。 对于此组合,我们在规则数组中找到具有x和y坐标的单元格应采用的状态。
优化选项 q=a[xm][ym]; q=(q<<1)+a[x][ym]; q=(q<<1)+a[xp][ym]; q=(q<<1)+a[xm][y]; q=(q<<1)+a[x][y]; q=(q<<1)+a[xp][y]; q=(q<<1)+a[xm][yp]; q=(q<<1)+a[x][yp]; q=(q<<1)+a[xp][yp]; temp[x][y]=rule[q];
在所有迭代之后,用新状态替换自动机的先前状态:
我们使用setInterval函数绘制一个自动机:
setInterval timerId = setInterval(function() { countpoints(); }, 1);
在浏览器中运行在继续阅读本文之前,我建议使用随机规则启动计算机10-20次。
我们可以使用不同的随机规则长时间运行计算机。 在没有信号的情况下,我们获得的图像将与电视屏幕上的图像没有不同:

接下来,让我们继续使用遗传算法设置“电视”。
遗传算法
初始人口为200台计算机(个人)。 对于规则,我们将使用二维填充数组来代替规则的一维数组。 第一个指数(n)是人口总数。
创建人口 var PopulationSize=200; var rulesize=512; var population=[]; var fitness=[]; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
适应度数组包含每个人的适应度系数。 在选择过程中将填充此数组。 选择之后,我们开始进化过程。
进化过程
从人口中,我们选出适应性最强(根据适应系数)的一半的人。 剩余的一半被摧毁。 接下来,我们带走两个幸存的个体,并将其穿过。

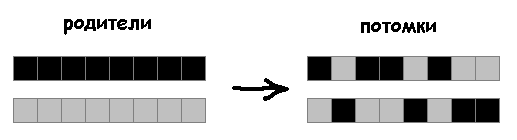
要进行杂交,请在两个祖先的基因型中选择一个随机位置。 在此职位之前,我们从一个祖先那里获取基因,在此职位之后-从另一个祖先那里获取基因。 我们将基因型中的选定基因带给一个后代。 剩下的基因是另一个。 我们将两个祖先和两个后代置于新的种群中。 同时,每个人都参加一次穿越。
变异。 每个个体中有一个随机选择的基因以5%的概率发生突变(反转)。 如果您增加突变的可能性,将会有更多成功的突变体,但是同时,一个成功的突变体可能没有时间离开成功的后代,而无法再次成功地进行突变。 我们稍后会再讨论这个问题。
函数evolute(); function evolute(){ var sizehalf=PopulationSize/2; var sizequarter=sizehalf/2; var arrayt=[]; for(var n=0; n<PopulationSize; n++) arrayt[n]=[population[n], fitness[n]]; arrayt.sort(sortf); arrayt.length=sizehalf; population=[]; fitness=[]; for(var i=0; i<sizequarter; i++){ var i0=i*4; var i1=i*4+1; var i2=i*4+2; var i3=i*4+3; var removed1=Math.floor(Math.random()*(arrayt.length)); var parent1f = arrayt.splice(removed1,1); var parent1=parent1f[0][0]; var removed2=Math.floor(Math.random()*(arrayt.length)); var parent2f = arrayt.splice(removed2,1); var parent2=parent2f[0][0]; var child1=[]; var child2=[]; var qen=Math.floor(Math.random()*rulesize); var temp0=parent1; var temp1=parent2; var temp2=temp0.splice(qen,rulesize); var temp3=temp1.splice(qen,rulesize); var parent1=temp0.concat(temp2); var parent2=temp1.concat(temp3); var child1=temp1.concat(temp2); var child2=temp0.concat(temp3); population[i0]=parent1; population[i1]=parent2; population[i2]=child1; population[i3]=child2; fitness[i0]=0; fitness[i1]=0; fitness[i2]=0; fitness[i3]=0; } var mutation=document.getElementById("mutatepercent").value*1; var m=100/mutation; var m2=0;
自然选择
在开始进化过程之前,必须进行选择。 选择可以是自然的也可以是人工的。 人工选择是手动进行的-稍后进行。 对于自然选择,我们将设置一些条件并选择最符合给定条件的机器。
可以预先确定哪些标准? 采取最简单的一种。 我们的“电视”闪烁太多。 我们保存了元胞自动机的两个状态-分别为99和100次迭代。 计算未更改的单元格数。 所得的数字将用作适应度系数。 显然,一个标准对我们来说还不够。 手动选择最能满足给定标准的自动机很容易:自动机[0,0,0,...,0]和自动机[1,1,1,...,1]。 第一次迭代时,这两个自动机将填充零或一,并停止更改其状态。 我们定义第二个标准:机器中0和1(单元)的数量之差不超过100(该数字是“从推土机中获取的”)。
array1-第99次迭代时自动机的状态。 array2-第100次迭代:
我们考虑 function countfitness(array1, array2){ var sum=0; var a0=0; var a1=0; for(var x=0;x<sizex;x++){ for(var y=0;y<sizey;y++){ if(array1[x][y]==array2[x][y]) sum++; if(array1[x][y]==0){ a0++; }else{ a1++; } } } if(Math.abs(a0-a1)<100) return sum; return 0; }
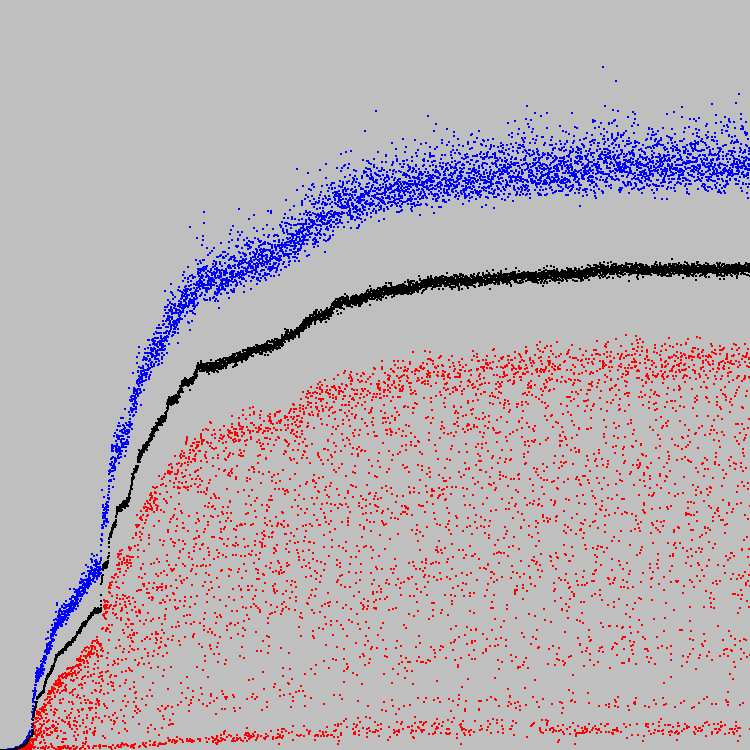
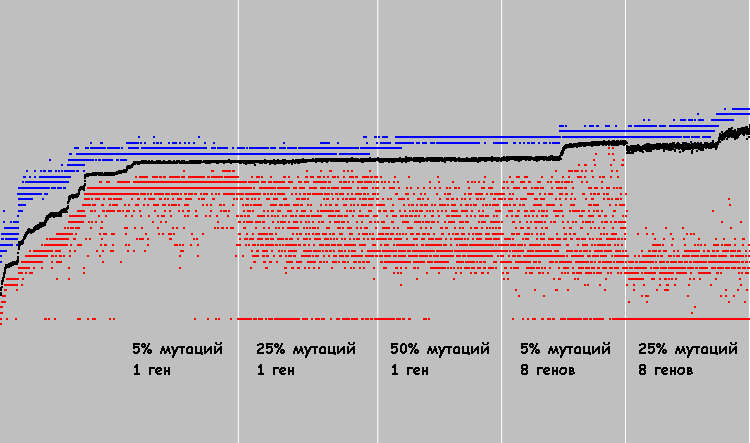
我们开始。 在进化的第421个循环中找到了最佳解。 在图表上,您可以看到进度:
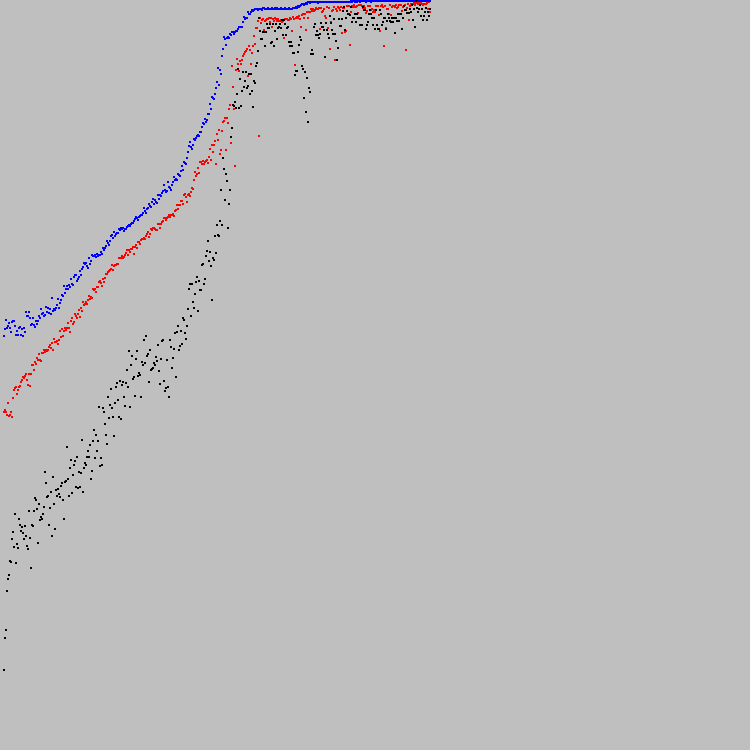
该图沿Y轴缩放,最低点为0,最高点为7921。很明显,7921是最佳解决方案(89x89机器中的所有单元格都满足指定的条件)。 经过100次迭代后,没有单元会更改其状态。
图表上的蓝点是总体中最好的个体。 红色是最差的(仅考虑满足第二个条件的个人)。 黑点-整个人群的平均适应系数(考虑到不符合第二个条件的个人)。 第二个标准(白色和黑色之间的平衡)非常严格。 一些自动机甚至在421个演化周期后仍不满足第二个条件。 因此,黑点在红色下方。
群体的基因库(个人沿Y轴,个人沿X轴):

让我们看看我们的“电视”捕获了哪个频道:

找到的解决方案不是唯一的最佳解决方案。 如果我们重新运行进化过程(使用随机初始基因型),我们将找到其他最佳解决方案。 其中之一:

更改选择标准。
我们将考虑在摩尔数为2的摩尔附近出现模式的像元数。 让我们采用最简单的模式:
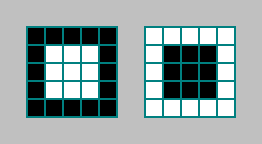
这个标准很有趣,因为我们检查了25个单元格,而自动机基于9个单元格的状态来计算单元格的状态。
该标准非常严格。 如果我们采用随机自动机,则经过100次迭代后,它看起来像这样:

在这种自动机中,没有一个单元格符合给定标准。 因此,我们将标准稍微软化:
- 让我们在模式上犯一个错误。
- 我们不会在最后一次迭代中搜索模式,而是在最近50次迭代中搜索。
第二个条件(白色和黑色之间的平衡)被删除。
我们开始。 图表:
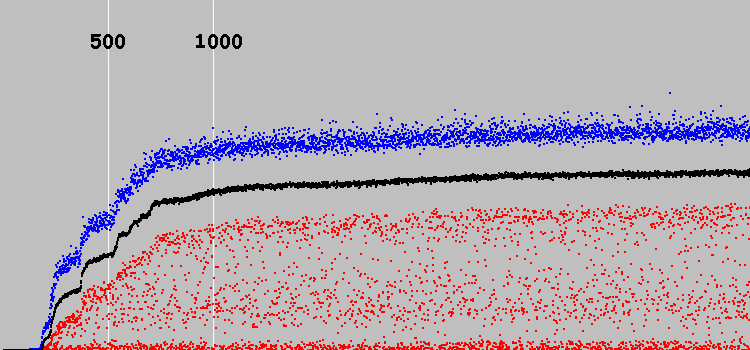
y轴是任意的。 (在以前的机器中,最佳解决方案是7921。在这台机器中,大约30。)
X轴-3569个演化周期。 两条白色垂直线标记了500和1000个进化周期。
蓝点-人口中最好的个人,红色-最差的人,黑色-整个人口的平均比例。
解决方案是在进化的前500个循环中找到的。 在接下来的500个循环中,解决方案得到了改善。 然后,该系统实际上停止了发展。
在以下三个图片中:500个周期,1000个周期和3569个演化周期:



基因库(3569):

在动力学方面:

在下面的图片中,您可以看到振荡器(滑翔机)在本机中的形成方式:

我们可以以填充一个单元格的初始状态启动机器。 接下来,修复在以下自动机迭代中找到的所有单元格组合。 基因阵列(自动机的基因型)是所有可能组合的阵列。 仅将出现的组合分离出来,我们可以轻松地注意到与振荡器形成有关的所有基因。 灰条是不参与振荡器形成的基因:

由于这些基因的突变会破坏模式的形成,因此不会生根。
在我们的机器中,仅在黑色单元周围形成图案(正方形)。 让我们尝试从第二条标准开始进化过程:白细胞和黑细胞数量之间的差异不超过400。
我们开始3569个进化周期。 图表:
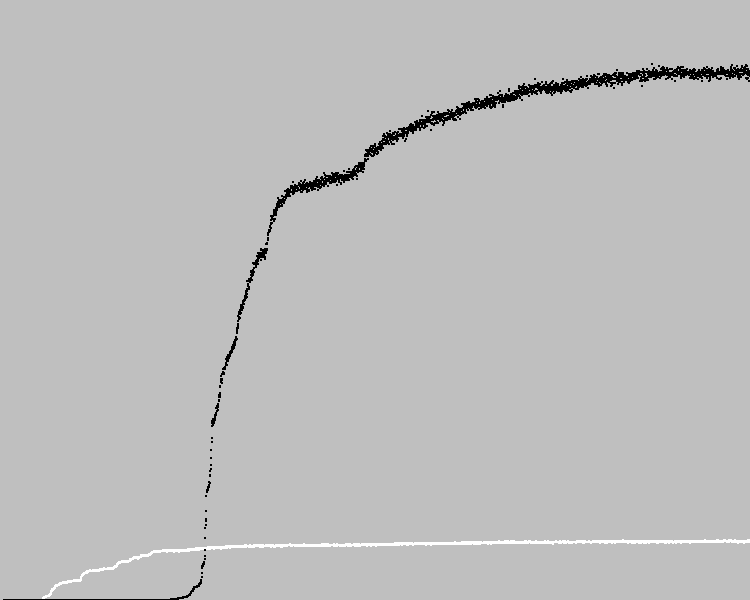
图中的黑点是总体中的平均适应系数。 白点-前一台机器的平均适应系数。 找到了模式中有一个错误的解决方案。
基因库:

100个第一次迭代:

最后(100)次迭代:

一点不是我们预期的结果。 有黑色正方形,白色-不。 收紧第二个标准:白细胞和黑细胞的数量之差不超过100。
我们开始了14865个进化周期。
该图比较了人口的平均适应系数。 蓝点是我们的机枪。 白色和黑色是以前的机器。

自动机发展得如此之猛,以至于它似乎根本就没有发展。 第二张图沿Y轴缩放,两条白线-500和1000个循环。
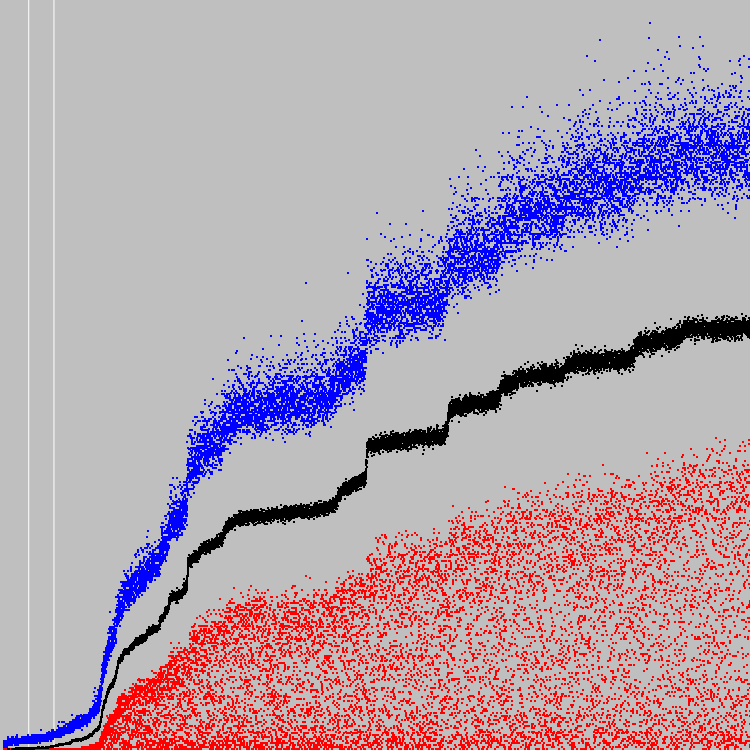
在最佳个体中,平均有6个单元格对应给定标准。
让我们看一看人口中的随机机器。
50次迭代:

最后(50)次迭代:

找不到可接受的结果。 第二个条件使搜索变得复杂,因此我们将拒绝它(我们将在本文后面不再使用它)。 让我们离开这个模式,寻找其他一些模式。
模式:

我们开始。 3000个进化周期。 图表:
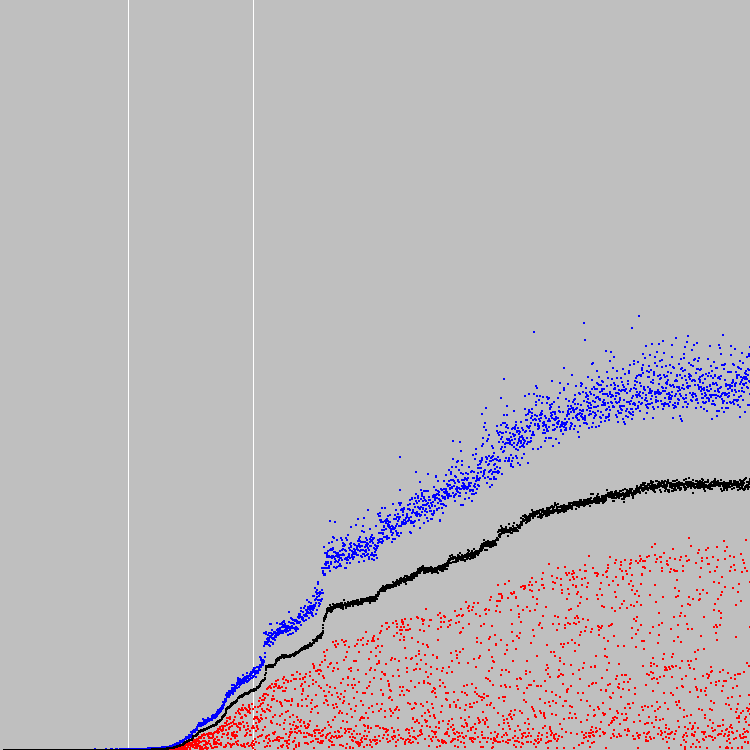
基因库:

在动力学中(100次迭代):

最后(100)次迭代:

模式:

在以前的机器中,我们允许在模式中犯一个错误。 这次,让我们寻找确切的模式。
我们开始4549个进化周期。 图表:
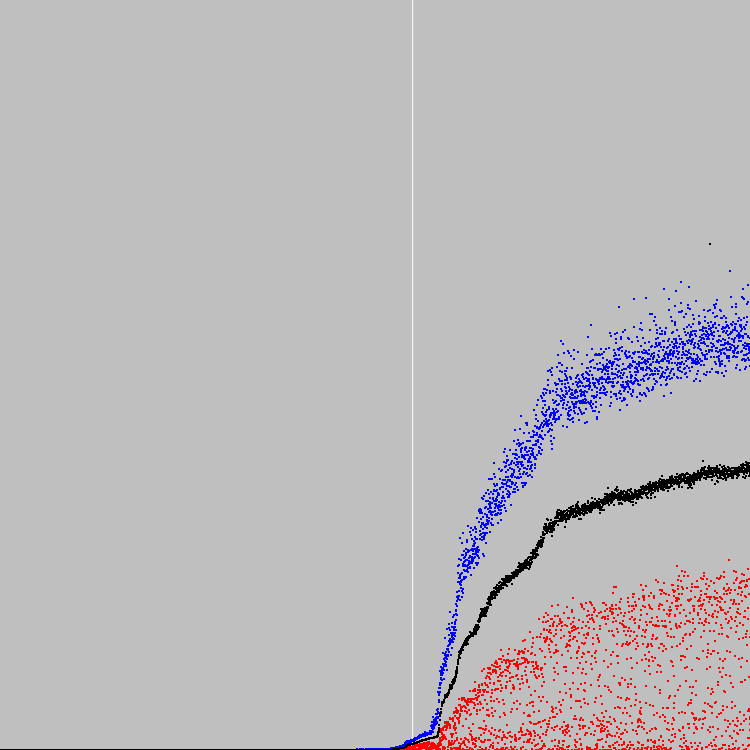
白色垂直线-2500个演化周期。 在这一点上(较早),人口的适应能力开始迅速增长。 节省了群众以寻求一个临时解决方案。 事实证明,中间解决方案比第4549个演化周期的解决方案有趣得多。
在第4549个演化周期中找到的解决方案:

Gif上有100次迭代。 经过一定数量的迭代(大约500-2000)后,自动机的状态几乎完全有序(自动机的高度和宽度由奇数专门选择,以使自动机无法完全有序):

经过一定数量的迭代后,具有均等大小的边的自动机处于完全有序的状态。 自动90x90,大约1200次迭代:

中间解决方案(在第2500个演化周期中发现):

该自动机还知道如何将某个初始混沌状态处理为某个有限有序状态(最终有序状态是模式沿着X轴向左移动+多个振荡器单元)。
16x16机器经过约100次迭代整理:

32x32-大约1000次迭代:

64x64-约6000次迭代:

90x90-约370000次迭代:

11x11(自动机字段的奇数维)-约178700次迭代:

13x13突击步枪在可接受的时间内没有精简。
在下图中,机器在第100,000次迭代的256x256字段上:

我建议在一个较大的领域中研究这种自动机的动力学-观察这种自动机中的混沌自组织过程非常有趣:
在浏览器中运行中级人群的基因库:

重新启动进化过程可以使您找到其他解决方案。 其中之一:


另一种模式:
搜索模式时,让我们再次犯一个错误(没有错误,具有所选模式的系统不会进化)。
我们开始。 5788个进化周期。 图表:
规模是任意的。
基因库:

在动力学方面:

自动机的有序状态(模式沿Y轴向上移动+多个振荡器单元):

更有趣的是,观察机器而不是机器,而是观察出现在该种群中的突变体:
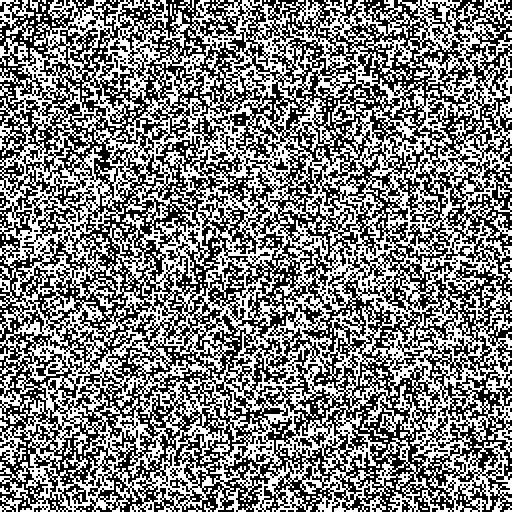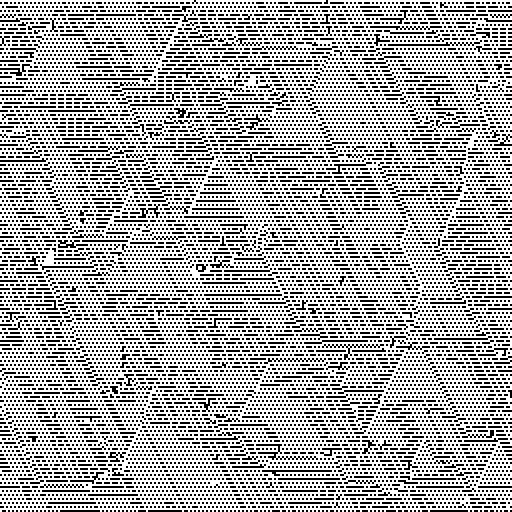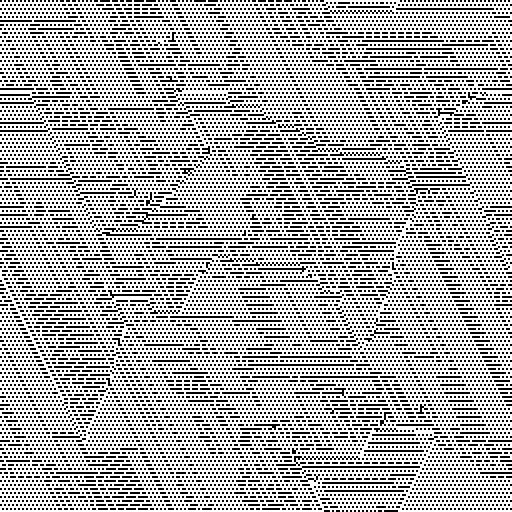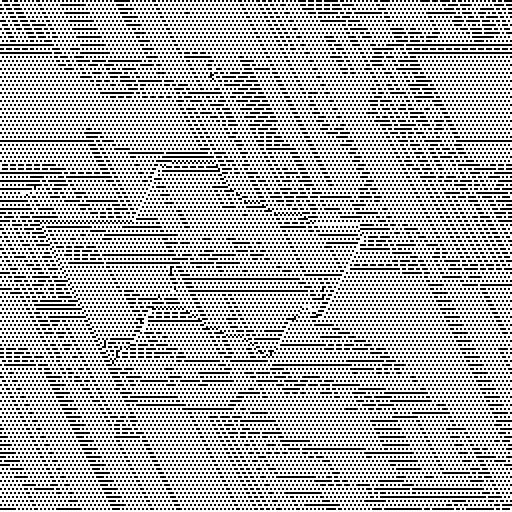
在Gif上,计算机为256x256。 200次迭代。 其余的迭代可以
在浏览器中查看 。
一个可以以自然选择结束,然后再进行人工选择,但我想展示一下
2512 数量庞大。 在此数量的自动机中,我们可以找到绘制任何给定图案的自动机(对于更复杂的图案,其准确性较高)。
以下模式:

在先前的实验中,我们计算了围绕其形成图案的像元的总和(如果有一个错误,则将总和加1,如果没有错误,则将其加2)。 将所得的量用作遗传算法的适应度因子。
对于更复杂的模式,此方法不起作用。 数量较少的单元格更紧密地匹配给定标准(与单元格附近的模式匹配的单元格的数量)的自动机每次都会丢失,其中数量较大的单元格不太精确地匹配给定标准的自动机。 如上面的正方形的示例所示:

对于所需的模式,在种群中每个自动机被第一个单元包围的第100次迭代中,我们将考虑与该模式匹配的单元数。 我们只会为每台机器取得最佳结果。 匹配模式的单元格数量将用作适应度因子。 模式由7x17 = 119个单元组成。 该数字将被视为最佳解决方案。 6000个进化周期使我们能够找到一个自动机,该自动机绘制有5个错误的模式(114个单元与该模式重合)。
任意比例的图形:
突变百分比的增加不会损害人群的健康。
种群的基因库中有许多突变体:

来自种群动态的随机自动机:

第100次迭代中最好的机器:

搜索和找到的模式:

考虑了选择标准,自动机字段的大小和突变的百分比后,事实证明可以改善总体并找到仅在模式中出现3个错误的自动机。
基因库:

第100次迭代的机器:

搜索和找到的模式:

2个错误在撰写本文的过程中,系统不断发展。 为了更精确地进行搜索,计算机字段的大小已增加到513x513。 发现一个自动机,该自动机仅在模式中出现两个错误:

在四个图中,您可以看到系统如何以不同的突变概率(1个基因突变)进化:
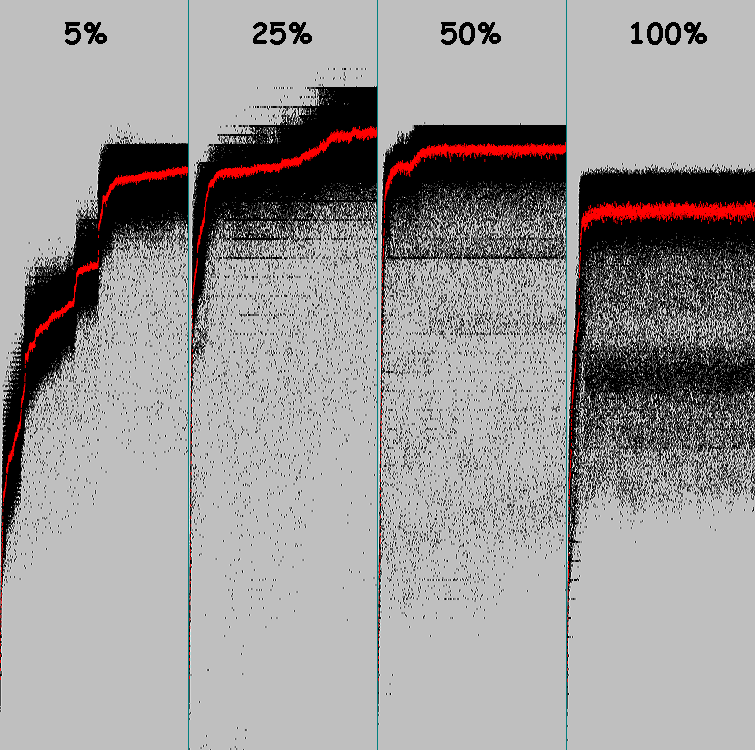
红点是总体中的平均适应系数。 黑点是每个人的适应系数。 每个系统3000个演化周期。
种群的基因库(按相同顺序):




第100次迭代的自动机:




让我们做另一个实验。 模式是相同的。 最初的基因型充满了随机基因。 发生突变的可能性为5%。 从1到8个基因发生突变(每个个体随机获取一个突变基因)。 100个进化周期。

该图是一个热图。 图表上的点大小为5像素。 原点是左上角。
在Y轴上(从0到100)-演化周期。 在X轴上(从0到119)-与模式一致的细胞数(对于种群中的每个个体,我们都获得最佳结果)。 点的亮度是具有指定(X坐标)结果的个人数量。
使用相同的参数(100个周期,5%的突变,最多8个基因突变)运行遗传算法4次。 在图中,所有5个开始:

以下是5个开始:25%的突变,最多8个基因突变:

样本很小,但是我们可以得出有关增加突变百分比的有效性的结论。
接下来,我将展示本文中使用的交叉方法的效率低下。
先前使用的方法:

后代将基因型分为两个部分,而不是将其分为两个部分:
5%突变:

25%:

接下来,我们将使用这种交叉方法。
在这与自然选择完成。 如果有人对自然选择的标准有有趣的想法-请在评论中表达他们的想法。
对于人工选择,我们将使用
二阶细胞自动机 。
二阶元胞自动机
考虑一阶的零维元胞自动机(我们上面考虑的所有元胞自动机都是一阶的)。 零维元胞自动机由一个像元组成。 一个单元可以处于两种状态之一。 单元格(t)的下一个状态由单元格(t-1)的当前状态确定。 总共有4个零维元胞自动机(其中一个是振荡器):
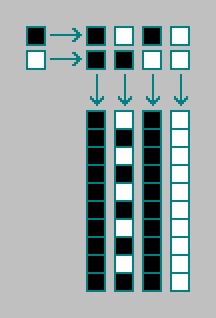
在二阶元胞自动机中,元胞的下一状态(t)由当前状态(t-1)和元胞的先前状态(t-2)确定。 总共有两个单元状态的4种组合。
24=$1 -二阶零维元胞自动机的数量:

这种细胞自动机表现出更复杂的振荡器。
28=256 三阶元胞自动机:
 216=65536
216=65536 一张图片无法显示四阶元胞自动机。
细胞自动机搜索 n 振荡周期等于的四阶 n -这项任务并不简单,而且非常有趣。 本主题值得另写一篇文章。在第二维一维细胞自动机中,一个单元格的下一个状态由三个单元格的当前状态和一个单元格的前一个状态确定:
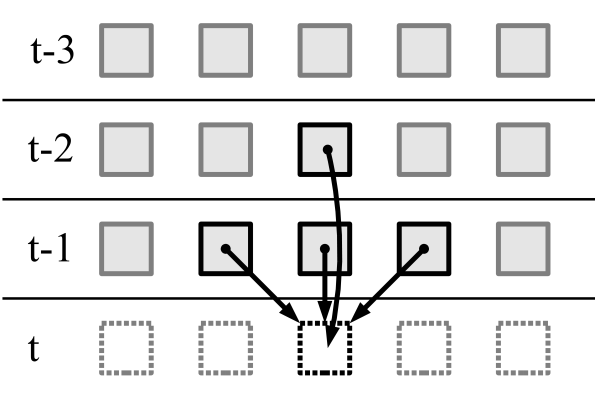
有
216=65536 一阶二阶元胞自动机。
代码:
var rule=[]; for(var i=0;i<16;i++) rule[i]=Math.round(Math.random()); var a=[]; var b=[]; var temp; for(var x=0;x<sizex;x++){ a[x]=0; b[x]=0; } b[63]=1; var xm, xp, q; for(var y=2;y<sizey;y++){ temp=[]; for(var x=0;x<sizex;x++){ xm=x-1; if(xm<0) xm=sizex+xm; xp=x+1; if(xp>=sizex) xp=xp-sizex; q=b[xm]; q=(q<<1)+b[x]; q=(q<<1)+b[xp]; q=(q<<1)+a[x]; temp[x]=rule[q]; if(temp[x]) context.fillRect(x*size, y*size, size, size); } a=b; b=temp; }
 0101101110011110:
0101101110011110: 0110000110010010:
0110000110010010: 0110011010010110:
0110011010010110: 1110011010010110:
1110011010010110: 0110111010000101:
0110111010000101: 1111101001110110:
1111101001110110: 1001010001100000:
1001010001100000: 同一台机器256x256:
同一台机器256x256: 512x512
512x512 在这里可以看到其他机器:二阶一维蜂窝机器。三阶一维元胞自动机。二阶一维元胞自动机可以在Wolfram的著作《一种新型的科学》中找到。
在这里可以看到其他机器:二阶一维蜂窝机器。三阶一维元胞自动机。二阶一维元胞自动机可以在Wolfram的著作《一种新型的科学》中找到。人工选择
像二阶的一维元胞自动机一样,在二阶的二维元胞自动机中,我们将使用来自自动机先前状态(t-2)的其他像元。为方便起见,我们将该单元格放在二进制行的开头: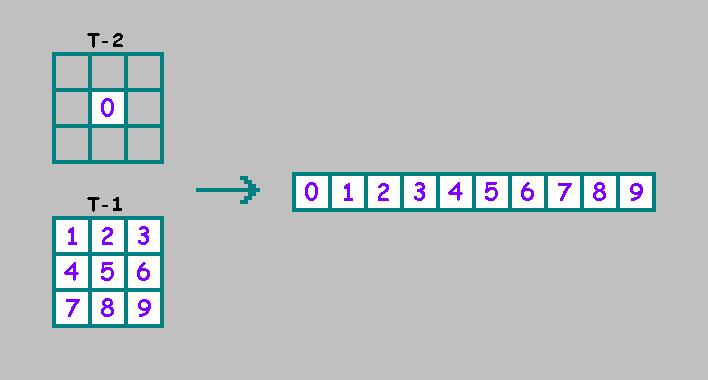 方便之处在于,当基因型的前半部分和后半部分重合时,自动机可以被视为一阶自动机:
方便之处在于,当基因型的前半部分和后半部分重合时,自动机可以被视为一阶自动机: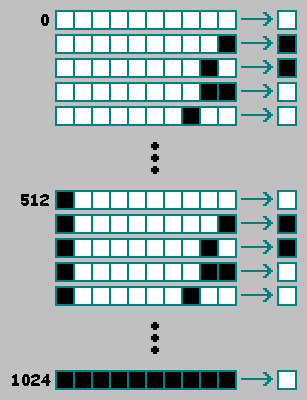 通过添加一个单元格,我们增加了现有自动机的数量。2 512倍。2 512 × 2 512 = 2 1024-二阶现有二维自动机的数量。对于自然选择,我们确定了一些标准,并根据此标准比较了自动机。在人工选择的过程中,我们使用一些模糊的原理手动选择机器:“这台机器很有趣,但不是很有趣。” 此原则不允许您在随机计算机中选择最佳计算机:有几种方法可以解决此问题。我建议考虑四种方式。
通过添加一个单元格,我们增加了现有自动机的数量。2 512倍。2 512 × 2 512 = 2 1024-二阶现有二维自动机的数量。对于自然选择,我们确定了一些标准,并根据此标准比较了自动机。在人工选择的过程中,我们使用一些模糊的原理手动选择机器:“这台机器很有趣,但不是很有趣。” 此原则不允许您在随机计算机中选择最佳计算机:有几种方法可以解决此问题。我建议考虑四种方式。





1.在机器的初始状态下,一个单元被填充
一种方法是观察细胞自动机的发展,在其初始状态下一个细胞被充满。我们用随机机器填充初始人口。初始种群中的几台机器(每个机器30次迭代):

 少数自动机表现出较少的混沌行为。我们将选择它们进行交叉:
少数自动机表现出较少的混沌行为。我们将选择它们进行交叉:




 从初始种群中选出20个随机机器(第30次迭代时的机器状态):
从初始种群中选出20个随机机器(第30次迭代时的机器状态): 经过三个演化周期:
经过三个演化周期: 经过八个演化
经过八个演化 周期:八个演化周期足以用具有特定特征的机器(绘制三角形的机器)填充整个种群。 。
周期:八个演化周期足以用具有特定特征的机器(绘制三角形的机器)填充整个种群。 。2.基因型已部分填充
如果违反了基因型中的单位和零的比率,则违反了表型中的单位和零的比率。在自动机的基因型(规则)中,记录了该单元格和相邻单元格的所有可能组合的以下单元格条件。如果基因型中有更多零(或一),则零(或一)会在以下自动机状态下累积。有趣的是,查看了基因型中1和0的比率与表型中1和0的比率之间的相关性。建立图表。创建200台计算机。我们用零填充基因型(二维二阶自动机的基因型中有1024个基因)。下一个n个基因充满单位。对于第一个人口n = 0,对于第513个人群n = 512 。
沿轴 x是人口数。沿轴y标志(带有白色圆点)在种群基因库中的一和零之比。我们得到了一个双曲线:对于每个自动机(字段大小为89x89),我们考虑100次迭代。在第100次迭代中,我们计算每个自动机的状态(表型)中的1和0的数量。我们在图上标记单位与零的比率(所有单位的总数除以所有零的总数)。我们得到一条曲线:您可以查看每种表型中的一和零的比率,而不是所有表型中的一和零的总比率:在图的左侧,存在与平均值偏差最大的点。可以假定它们是零基因的基因型为1的自动机。假设-已选中。我们将零基因设置为始终等于零。我们绘制一个新图表: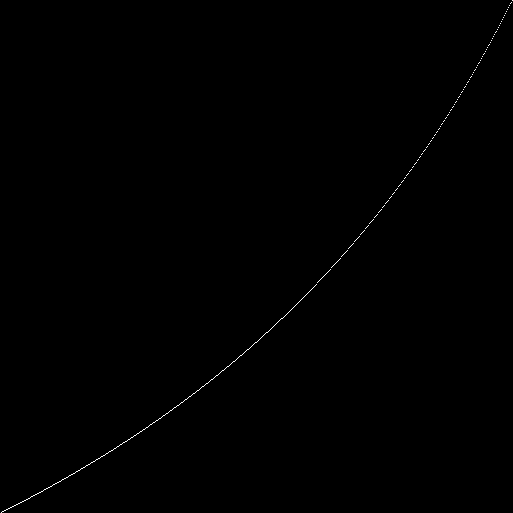
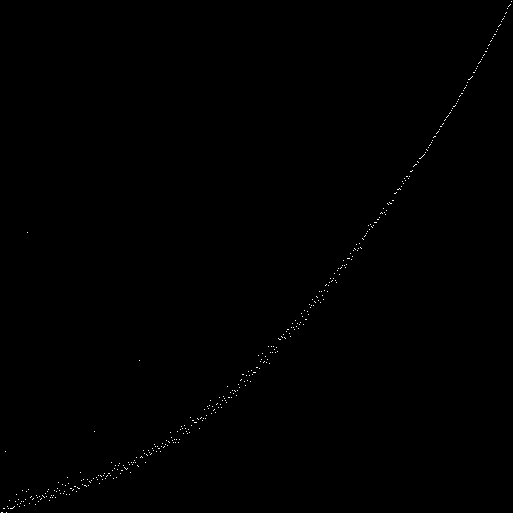

 与零基因始终等于1的机器进行比较:
与零基因始终等于1的机器进行比较: 在二阶机器中,还有另一个“零”基因-第512个基因。让我们看看这个基因如何影响表型。第0和512个基因始终为零:第
在二阶机器中,还有另一个“零”基因-第512个基因。让我们看看这个基因如何影响表型。第0和512个基因始终为零:第 0个基因始终为零。第512个基因始终等于1:
0个基因始终为零。第512个基因始终等于1: 为了不再次嘲笑我们尊敬的癫痫病患者,在遗传算法的初始种群中,第0和512个基因将被零填充。让我们看一下通过将零设置为0th和512th基因而摆脱的机器。自动机的前8个状态,其中仅填充第0个基因(零基因为一个,其余为零):一个
为了不再次嘲笑我们尊敬的癫痫病患者,在遗传算法的初始种群中,第0和512个基因将被零填充。让我们看一下通过将零设置为0th和512th基因而摆脱的机器。自动机的前8个状态,其中仅填充第0个基因(零基因为一个,其余为零):一个 自动机,其中仅
自动机,其中仅 填充第512个基因:一个自动机,其中仅填充第0个和第512个基因:
填充第512个基因:一个自动机,其中仅填充第0个和第512个基因: 让我们在图中开始一个区域,在该位置上,人口开始分为几类:
让我们在图中开始一个区域,在该位置上,人口开始分为几类: 在这个地方,基因型已填充25%。比较两个人口。第一人口。第1000次迭代有30台随机计算机。基因型已满50%(512个单位和512个零):
在这个地方,基因型已填充25%。比较两个人口。第一人口。第1000次迭代有30台随机计算机。基因型已满50%(512个单位和512个零): 第二个种群。第1000次迭代有30台随机计算机。基因型已满25%(256个单位和768个零):
第二个种群。第1000次迭代有30台随机计算机。基因型已满25%(256个单位和768个零): 第二个种群适合人工选择。我们可以轻松地突出显示此类机器中的一些标志。例如:“较暗”,“较少混乱”(将白细胞分组的自动机)等。我们选择“较暗”。突变的可能性是10%,最多4个基因发生突变。在第一次选择
第二个种群适合人工选择。我们可以轻松地突出显示此类机器中的一些标志。例如:“较暗”,“较少混乱”(将白细胞分组的自动机)等。我们选择“较暗”。突变的可能性是10%,最多4个基因发生突变。在第一次选择 之后:在第二次选择之后:
之后:在第二次选择之后: 种群中出现了一个有趣的自动机。256x256,计算机在第1000次迭代时的状态:
种群中出现了一个有趣的自动机。256x256,计算机在第1000次迭代时的状态: 计算机逐渐填充总体。第八次选择之后:
计算机逐渐填充总体。第八次选择之后: 另一个有趣的机器出现了。256x256,第1000次迭代时自动机的状态:
另一个有趣的机器出现了。256x256,第1000次迭代时自动机的状态: 十三次选择后的
十三次选择后的 总体:此总体中的几个自动机。256x256,每个人的第1000次迭代。图片下方是一个链接,单击该链接,您可以动态
总体:此总体中的几个自动机。256x256,每个人的第1000次迭代。图片下方是一个链接,单击该链接,您可以动态 查看 机器:动态查看。
查看 机器:动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。 动态查看。
动态查看。3.康威自动机等
一阶最著名的二维元胞自动机是Conway自动机游戏“生活”。Conway自动机的规则编写如下:如果一个死细胞周围有3个活细胞,则该细胞会活着(否则它将保持死状态)。如果一个活细胞周围有2或3个活细胞,则该细胞将保持存活(否则死亡)。死单元是0,活单元是1。一个单元周围可以是0到8个活单元。根据围绕活细胞和死细胞的9种选择。我们将所有选项写入r数组:数组 r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ];
阵列的前半部分用于死细胞,后半部分用于活细胞。我们可以为一个像元和8个相邻像元的所有可能(512)组合描述Conway自动机的规则:画规则 r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; var q1, q2; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[1]+1*ii[2]+1*ii[3]+1*ii[5]+1*ii[6]+1*ii[7]+1*ii[8]; if(q1==0) rule[i]=r[q2]; else rule[i]=r[q2+9]; }
优化选项 r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; for(var i=0;i<512;i++){ var q=((i>>4)&1)*8; for(var j=0;j<9;j++){ q+=(i>>j)&1; } rule[i]=r[q]; }
对于二阶自动机,请从前一个复制规则数组的后半部分:复制 for(var i=0;i<512;i++){ if(rule[i]==0) rule[i+512]=0; else rule[i+512]=1; }
我们使用指定的规则启动计算机。我们看到了典型的滑翔机和振荡器。此自动机的几次迭代: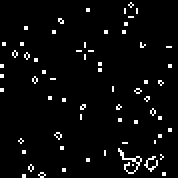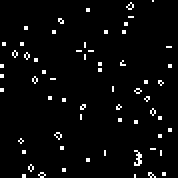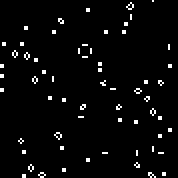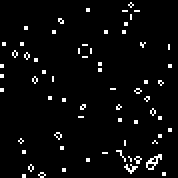 数组r由18个像元组成。有2 18 = 262144自动机,类似于Conway自动机(可以用相同的规则来写:被死者包围的活细胞的数量,其中有生命的细胞得以存活;处于死亡环境中的活细胞的数量,其中细胞死亡)。您可以在此处查看它们(默认情况下,Conway自动机启动,“更改规则”按钮随机填充r数组)。几个随机机器(二进制代码-数组R):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111
数组r由18个像元组成。有2 18 = 262144自动机,类似于Conway自动机(可以用相同的规则来写:被死者包围的活细胞的数量,其中有生命的细胞得以存活;处于死亡环境中的活细胞的数量,其中细胞死亡)。您可以在此处查看它们(默认情况下,Conway自动机启动,“更改规则”按钮随机填充r数组)。几个随机机器(二进制代码-数组R):110010011001111111100001100110111110011111000100101110010000110000110010001111010011100111000111001000000110000101100010100001000001111101011111000001100110111111






 对于遗传算法,作为基因型,可以使用数组r( 2 18个组合)和规则数组(2个512的元胞自动机的第一级的组合和2 1024-用于二阶元胞自动机)。2 18是相对较小的数字。此数字使您可以手动选择计算机的规则,而无需使用遗传算法(实际上是Conway所做的)。如果您用这种类型的随机计算机填充规则数组并将此数组用作基因型,则在某种程度上可以认为该实验是不成功的(足够在本文中未显示该实验的结果)。在这种类型的细胞自动机规则中,存在对称性。例如,对于以下单元格组合:
对于遗传算法,作为基因型,可以使用数组r( 2 18个组合)和规则数组(2个512的元胞自动机的第一级的组合和2 1024-用于二阶元胞自动机)。2 18是相对较小的数字。此数字使您可以手动选择计算机的规则,而无需使用遗传算法(实际上是Conway所做的)。如果您用这种类型的随机计算机填充规则数组并将此数组用作基因型,则在某种程度上可以认为该实验是不成功的(足够在本文中未显示该实验的结果)。在这种类型的细胞自动机规则中,存在对称性。例如,对于以下单元格组合: 下次迭代时单元的状态是相同的。第一次穿越后,后代个体规则中的对称性被打破。祖先个体积累的突变也破坏了对称性。基因型中对称性的违反导致表型中对称性的违反。如果一个细胞在自动机的初始状态下被填充,则可以在表型上看到这种对称性的表现。让我们做一个实验。为了保持对称,我们将使用r数组作为基因型。 5%的突变,1个基因突变。在初始状态下,将填充一个单元格。初始人口中有30台随机机器。第30次迭代的自动机状态:
下次迭代时单元的状态是相同的。第一次穿越后,后代个体规则中的对称性被打破。祖先个体积累的突变也破坏了对称性。基因型中对称性的违反导致表型中对称性的违反。如果一个细胞在自动机的初始状态下被填充,则可以在表型上看到这种对称性的表现。让我们做一个实验。为了保持对称,我们将使用r数组作为基因型。 5%的突变,1个基因突变。在初始状态下,将填充一个单元格。初始人口中有30台随机机器。第30次迭代的自动机状态: 让我们尝试从一个细胞中分离最缓慢(生长)的自动机。
让我们尝试从一个细胞中分离最缓慢(生长)的自动机。



 第一次选择后,他们摆脱了不会发展的自动机:
第一次选择后,他们摆脱了不会发展的自动机: 在新种群中,有几种这样的自动机(不发展)-它们是不成功的后代和突变体。接下来,我们将主要选择具有白色背景的机器(该机器尚未显影的单元格)。
在新种群中,有几种这样的自动机(不发展)-它们是不成功的后代和突变体。接下来,我们将主要选择具有白色背景的机器(该机器尚未显影的单元格)。黑色自动售货机闪烁。( — ) — . ( ) ( ). . — () . ( — , — ). 30- , — . ( 30- ) — ( ).
第二个选择之后的填充: 3个选择:
3个选择: 5个选择:
5个选择: 8个选择:
8个选择: 13个选择:
13个选择: 第60次迭代时相同的机器:
第60次迭代时相同的机器: 21个选择。第30次迭代
21个选择。第30次迭代 的自动机状态:第60次迭代的自动机状态:
的自动机状态:第60次迭代的自动机状态: 34个选择。第30次迭代
34个选择。第30次迭代 的自动机状态:第60次迭代的自动机状态:
的自动机状态:第60次迭代的自动机状态: 此外,系统不进化。此总体中的三个自动机(每次100次迭代):[1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1,1]
此外,系统不进化。此总体中的三个自动机(每次100次迭代):[1,0,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1,1] [1 ,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1]
[1 ,0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,1,1,1] [1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1,1]
[1,0,0,1,1,0,0, 1,1,0,1,0,1,1,0,1,1,1,1] 作为比较,随机机器:[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]
作为比较,随机机器:[1,0,0,1,1,1,0,1,1,1,0, 0,1,1,0,0,0,1]
4. Conway自动机等(2)
在具有Conway类型规则的机器中,我们计算Moore附近细胞的存活数量(单位)。该邻域可以分为4对,并计算这些对中的活细胞数量: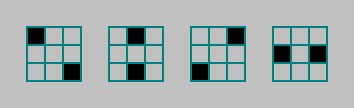 因此,我们增加了自动机的数量,但保持了表型的对称性。每对可以有0到2个活细胞。参数4.组合数3 4 = 81
因此,我们增加了自动机的数量,但保持了表型的对称性。每对可以有0到2个活细胞。参数4.组合数3 4 = 81 。
根据第81种组合,围绕活细胞和死细胞。总计存在2 162台此类自动机器。号码:2 162 ≈ 5846 × 10 48
它完全是天文数字,适合遗传算法。每个个体的基因型大小为162个基因:用随机机填充人群 var rulesize=162; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }
接下来,我们为一个单元格和八个相邻单元格的所有可能组合绘制此规则:函数fillrule(); function fillrule(){ var r; for(var n=0;n<PopulationSize;n++){ rule[n]=[]; r=population[n]; var q1, q2, q3, q4, q5; var q; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[8]; q3=1*ii[1]+1*ii[7]; q4=1*ii[2]+1*ii[6]; q5=1*ii[3]+1*ii[5]; q=parseInt(''+q2+q3+q4+q5,3); if(q1==0) rule[n][i]=r[q]; else rule[n][i]=r[q+81]; } } }
在计算自动机的下一个状态时,我们将使用规则数组。我们在加载页面之后和调用evolute()函数之后调用fillrule()函数。最初的人口看起来很混乱。 30台随机机器,第1000次迭代: 这种混乱在动态方面略有不同,这些机器非常适合选择,但让我们更容易些-我们将选择“最黑”的机器。五种选择后的填充:
这种混乱在动态方面略有不同,这些机器非常适合选择,但让我们更容易些-我们将选择“最黑”的机器。五种选择后的填充: 接下来,您可以搜索具有最复杂振荡器的机器。整个布局过程毫无意义。以下是使用遗传算法发现的一些最有趣的自动机。256x256,每个人的第10000次迭代。图片下方是一个链接,单击该链接,您可以动态查看机器:动态
接下来,您可以搜索具有最复杂振荡器的机器。整个布局过程毫无意义。以下是使用遗传算法发现的一些最有趣的自动机。256x256,每个人的第10000次迭代。图片下方是一个链接,单击该链接,您可以动态查看机器:动态 查看。
查看。 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.?
您可以在这里玩:二阶二维元胞自动机。界面: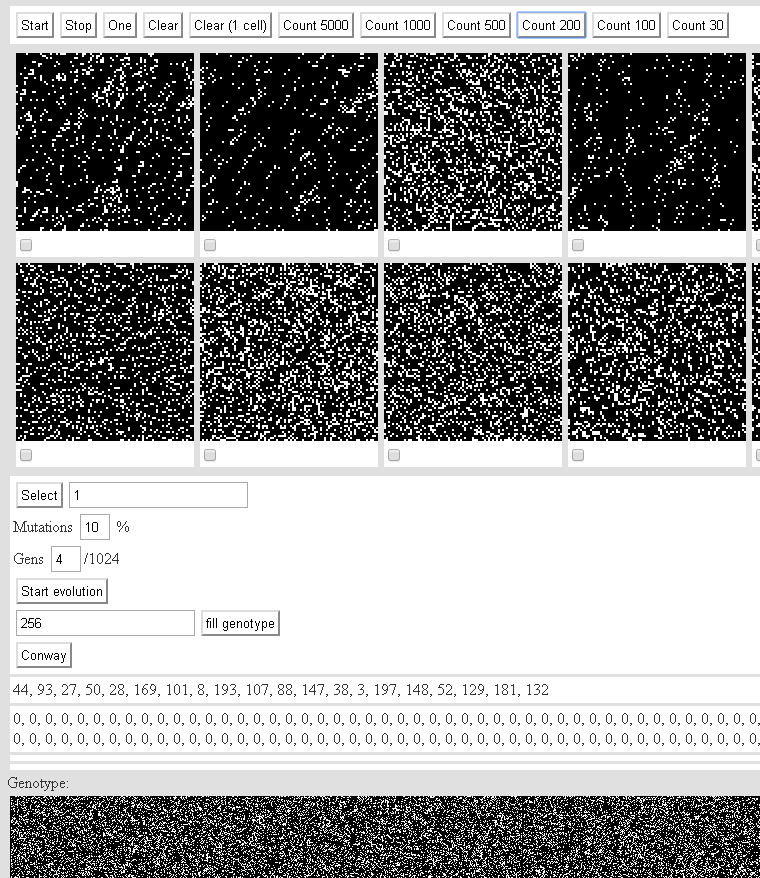 “开始”按钮启动机器。停止-停止。一是一迭代。清除-停止机器并随机填充初始状态。清除(1个单元格)-停止机器并在初始状态下填充一个单元格。该行上的其余按钮为每个自动机计数指定的迭代次数。在画布上渲染自动机会消耗所有性能。如果您需要快速计算200次迭代,请点击Count200。我们不需要点击Count 5000按钮-浏览器可以将其挂起。低于20台随机计算机(人口规模-200台计算机)。在自动售货机下的复选框。我们标记了最有趣的。按选择-机器的适用性将增加右侧指示的数字。突变-突变的可能性。基因是突变基因的数量。开始进化-启动杂交和突变机制。填充基因型-在每个自动机的基因型中填充指定数量的基因。康威(Conway)-用Konveevsky型机器填满人口。下面是两行:显示的机器编号。fenotype数组的内容。人口的基因库甚至更低。所有进度都存储在本地存储中。您可以在此处使用Konveevsky型突击步枪(以及本文中最后考虑的突击步枪):4. Conway自动机等(2)。
“开始”按钮启动机器。停止-停止。一是一迭代。清除-停止机器并随机填充初始状态。清除(1个单元格)-停止机器并在初始状态下填充一个单元格。该行上的其余按钮为每个自动机计数指定的迭代次数。在画布上渲染自动机会消耗所有性能。如果您需要快速计算200次迭代,请点击Count200。我们不需要点击Count 5000按钮-浏览器可以将其挂起。低于20台随机计算机(人口规模-200台计算机)。在自动售货机下的复选框。我们标记了最有趣的。按选择-机器的适用性将增加右侧指示的数字。突变-突变的可能性。基因是突变基因的数量。开始进化-启动杂交和突变机制。填充基因型-在每个自动机的基因型中填充指定数量的基因。康威(Conway)-用Konveevsky型机器填满人口。下面是两行:显示的机器编号。fenotype数组的内容。人口的基因库甚至更低。所有进度都存储在本地存储中。您可以在此处使用Konveevsky型突击步枪(以及本文中最后考虑的突击步枪):4. Conway自动机等(2)。