🤹🏻 🐣 🐲 三维超球体的世界。具有球形几何形状的封闭宇宙中的测地线追踪 👨🏾‍✈️ 🥁 💇🏼

您是否想通过生活在球形球形紧凑封闭宇宙中的生物的眼睛看世界？看到世界没有一夜？一个在天空中可以看到行星另一极的世界？日食与月食之间没有区别的世界吗？欢迎来到猫！

引言二维封闭世界

为了更好地理解下一步将发生的情况，请想象您是一个二维生物，并且生活在一个代表球体的二维世界中。您将如何看待自己的世界？让我们从确定物体的位置开始。您可以声明您是“宇宙中心”的点，选择两个相互垂直的单位矢量，并在“宇宙中心”附近使用生成的笛卡尔坐标系。

但是，当您离开“宇宙中心”时，奇怪的事情就会开始发生。与“宇宙中心”相距一定距离的垂直线变成了平行线...

...平行线相交。

原因很简单-您认为直线实际上是一个大圆 -球的测地线。因此，笛卡尔坐标系不适合确定物体在世界中的位置-当您离开“宇宙中心”时，它就失去了意义。

您将不得不选择另一个更适合您的世界的坐标系统-polar 。该坐标系是自然且一致的。确实-极轴与到身体的方向之间的角度保持恒定，而不管到身体的距离如何。

能够确定物体的位置，我们可以在精神上探索您的世界，并描述当您离开“宇宙中心”并且由于您的世界是一个球体而出现的某些效果。

相反的观点。 通常，当物体远离“宇宙中心”移动时，其角度大小会减小。但是，随着人体的离开，测地线距离“宇宙中心”的距离超过四分之一线的长度，其角度大小将增加。该效果是由于以下事实：球体的测地线到赤道之间的距离增加，而在赤道之后减小。距赤道相同距离的物体将具有相同的角度大小，而不管其位于赤道的哪一侧。并且该角度大小将大于赤道上物体的角度大小。

全身伸向天空。 在这里，术语“整个天空”的含义是-二维物体的整个视场（上下左右或前后左右）。如果身体位于与“宇宙中心”相对的点附近，那么无论您在哪里看，都将与这个身体相遇。身体不会有一个看不见的点-每个点在天空中都有一个位置。这是反向透视效果的最终案例。

对称转换电话。 如果物体与“宇宙中心”的距离等于测地线长度的一半以上，那么您将看到该物体对称变形-物体的左右两侧将改变位置。通常，从“宇宙中心”发出的左右光线落在身体的左右两侧。但是，从“宇宙中心”到测地线的长度的一半距离处，光线相交并且相交后落入人体的相对两侧。

第二种向前和向后的观点。 如果物体距“宇宙中心”的距离大于测地线长度的一半，也会观察到这种效果。从“宇宙中心”到测地线长度的一半到四分之三的距离处，随着物体的移走，其角度大小将再次减小（直接透视）。在距“宇宙中心”四分之三点到测地线的整个长度的距离处，随着身体的移动，其角度大小将再次增加（反向透视）。这种效果以及反透视效果与球的测地线之间的距离变化有关-在返回“宇宙中心”的过程中，球的测地线到赤道之间的距离增加，在赤道之后减小。

双打。 世界上的每个身体都会有一个双体-如果您看到前方有一个体，那么转身就可以看到其另一侧（双体）。沿着很长的路径发射的射线绕过您的世界，并进入身体的后部。应当注意，双精度曲面的表面将是您在您面前看不到的那部分表面，并且它将对称地变形。在这里，术语``表面''的含义是-由二维存在的物体感知的二维物体的边界-应用于圆时，我们实际上是在讨论以二维存在的物体作为分段的圆的弧，但是为了清楚起见，我们不仅会突出显示弧，还会突出显示位于其后面的圆的一部分。

身体通过与“宇宙中心”相对的点的通道。 由于将身体伸展到整个天空的效果非常不寻常，因此我们将对其进行更详细的考虑。在图中：与“宇宙中心”相对的点的邻域。

可以看出：

首先，您前面的身体表面增大（涂成蓝色），后面的身体表面减小（涂成蓝色）；同时，两个表面都具有相同的角度尺寸-也就是说，位于您前面的物体的表面会收缩（该表面的较大部分位于每个度数之内），而位于您身后的那个表面会被拉伸（该表面的所有较小部分位于每个度数之内）
当身体接触与“宇宙中心”相对的点时，两个表面的角度大小均为180度-天空的一半（在您的前面）占据了整个身体的表面，而天空的后半部分（在您的后面）被位于身体背面的一个点占据
当身体的中心与“宇宙的中心”相对的点对齐时，反向拉伸和拉伸的过程
当身体位于与“宇宙中心”相对的点时，其表面在整个天空上都不会变形
从“宇宙中心”对面滑动的身体看起来类似

双重视野。 想象一下，你生活在一个二维星球上。往下看，您会看到行星侧面的表面，往上看，您会看到……行星背面的表面。此外，它会非常紧-您可以看到行星背面的表面以及行星侧面的一部分在地平线后面的背面-您可以在头顶看到所有这些。天空将以细条状呈现，就像一条细线，从上方和下方由您和行星背面的视线夹在中间。这是在整个天空上伸展身体的效果和两倍效果的结合。一般而言，在您的世界中，如果没有任何事物打扰您的视线，那么在您的眼前就可以看到您的颈背……如此健康的颈背，其所有细节……延伸到整个天空）

没有夜晚的世界。 想象一下，您生活的二维星球围绕一个二维恒星旋转。恒星在短路径上发出的光落在行星的白天。同时，恒星沿着很长的路径发出的光会绕过您的世界，并落在行星的夜侧。夜晚不再存在。剩下的就是同时发生的日落和日出-当面向您的恒星侧面开始超出地平线时，恒星的背面将开始从地平线后面向后升起。当然，您可以沿光线通过的路径突出显示真正的日落和黎明，但是几乎不可能将它们与双倍区域区分开。

还有一个极端的情况。如果行星不走运并且位于对面恒星的位置，那么该恒星将在整个天空中伸展，但是佩服它会存在问题，因为恒星发出的所有光都将落在行星上（在行星际介质不吸收和散射光的情况下）。

日食和月食。 想象一下，一个二维自然卫星围绕着您所生活的二维行星旋转。当卫星进入行星和恒星之间时，其阴影落在行星上。另一方面，与此同时，行星位于恒星沿长路径发射的光与人造卫星之间，也就是说，行星的阴影落在人造卫星上。同时发生日食和月食。当然，可以沿光通过的路径的长度区分真正的日食和月食，但是实际上将它们与双胞胎区分开是不可能的。在日食时掉入落在行星及其卫星上的阴影是在世界上处于黑暗中的唯一方法）

三维封闭世界

上面，我们研究了二维生物的奇妙世界。那我们的三维生物呢？宇宙的几何形状是什么？不幸的是，科学还不能回答这个问题。主要是宇宙的性质和大小相互干扰。让我们尝试帮助科学。我们选择具有球形几何形状的最有趣的封闭宇宙作为候选对象，并对其进行目视检查。我们会为二维模拟发现一些影响吗？也许我们会学到新的东西？您没想到的事吗？甚至看到我们每天看到的东西，但不注意它？这样的宇宙会是什么样？

型号

我们将探索这个世界，它是一个三维超球面（3球），也就是一个位于四维空间中的球。我们选择一种类型的对象进行可视化-球体（属于3球体的2球体）。

基本概念和关系

三维空间中的笛卡尔坐标 -我们将其表示为

（ ， ， ， ）

$（x_0，x_1，x_2，x_3）$ -这实际上是

（ ， ， ， ）

$（x，y，z，w）$ 。

二维空间中的超球坐标 （我们仅使用角度，因为我们的世界半径将是一个常数）-我们将它们表示为

（ ， ， ）

$（a_0，a_1，a_2）$ -这实际上是

（ ， ， ）

$（\ phi，\ theta，\ psi）$ 。

以原点为中心的3球面 -一组点的半径矢量的长度等于3球体的半径

$R$ 是我们的世界

$\ quad \ quad x_0 ^ 2 + x_1 ^ 2 + x_2 ^ 2 + x_3 ^ 2 = R ^ 2$

属于3球的2球 -半径向量的长度等于3球的半径的一组点

$R$ 并以2球体中心的半径向量形成

$c$ 角度等于2球的角半径

$r_a$ 是我们的可视化对象

$\ quad \ quad x_0 c_0 + x_1 c_1 + x_2 c_2 + x_3 c_3 = R ^ 2 \ cos r_a$

在哪里

$\ Quad \ Quad r_a = r / R$

$\ Quad \ Quad R$ -2球的测地线半径

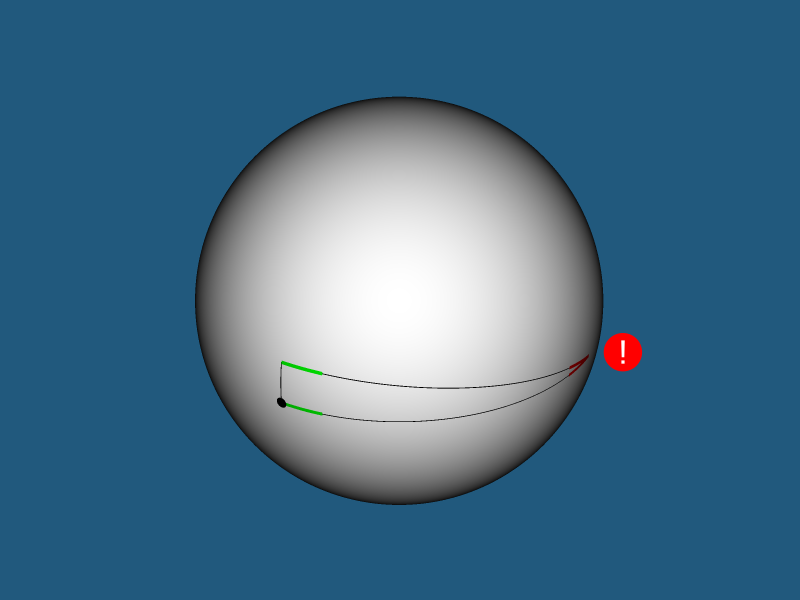
测地线，角线和条件半径 -为了更好地理解它的含义，请考虑属于3个球体的2个球体（属于一个球体的圆）的二维模拟。

图中的红色弧是圆的测地线半径

。图右侧的红色角是圆的角半径

$r_a = r / R$ 。图右侧三角形的高度是圆的条件半径

$r_n = R \ sin r_a$ 。

从超球面坐标过渡

$（a_0，a_1，a_2）$ 到笛卡尔

$（x_0，x_1，x_2，x_3）$

$\ Quad \ Quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ Quad \ Quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ Quad \ Quad x_2 = R \ sin a_2 \ cos a_1$

$\ Quad \ Quad x_3 = R \ cos a_2$

在哪里

$\ Quad \ Quad a_0$ 从

$0$ 之前

$2 \ pi$

$\ Quad \ Quad a_1$ 从

$0$ 之前

$\ pi$

$\ Quad \ Quad a_2$ 从

$0$ 之前

$\ pi$

3球的测地线与属于3球的2球的交点。
该比率将用于光线跟踪。设一条从3球极延伸的测地线

$（0，0，0，R）$ 在角度定义的方向上

$a_0$ 和

$a_1$ -这些角度与确定3球极附近的三维空间方向的角度一致

$（0，0，0，R）$

$\ Quad \ Quad x_0 = R \ sin a_2 \ sin a_1 \ cos a_0$

$\ Quad \ Quad x_1 = R \ sin a_2 \ sin a_1 \ sin a_0$

$\ Quad \ Quad x_2 = R \ sin a_2 \ cos a_1$

$\ Quad \ Quad x_3 = R \ cos a_2$

简化我们有（1）

$\ Quad \ Quad x_0 = r_0 \ sin a_2$

$\ Quad \ Quad x_1 = r_1 \ sin a_2$

$\ Quad \ Quad x_2 = r_2 \ sin a_2$

$\ Quad \ Quad x_3 = r_3 \ cos a_2$

在哪里

$\ Quad \ Quad r_0 = R \ sin a_1 \ cos a_0$

$\ Quad \ Quad r_1 = R \ sin a_1 \ sin a_0$

$\ Quad \ Quad r_2 = R \ cos a_1$

$\四元\四元r_3 = R$

将（1）代入2球面方程并简化，我们得到（2）

$\ Quad \ Quad A \ sin a_2 + B \ cos a_2 = C$

在哪里

$\ Quad \ Quad A = r_0 c_0 + r_1 c_1 + r_2 c_2$

$\ Quad \ Quad B = r_3 c_3$

$\ Quad \ Quad C = R ^ 2 \ cos r_a$

将（1）代入3球的方程式并进行简化，我们得到（3）

$\ Quad \ Quad D \ sin ^ 2 a_2 + E \ cos ^ 2 a_2 = F$

在哪里

$\ Quad \ Quad D = r_0 ^ 2 + r_1 ^ 2 + r_2 ^ 2$

$\ Quad \ Quad E = r_3 ^ 2$

$\ Quad \ Quad F = R ^ 2$

从（2）表示

$\ cos a_2$ 我们有

$\ Quad \ Quad \ cos a_2 =（C-A \ sin a_2）/ B$

代以（3）

$\ cos a_2$ 我们有

$\ Quad \ Quad D \ sin ^ 2 a_2 + E / B ^ 2（C-A \ sin a_2）^ 2 = F$

简化我们有

$\ Quad \ Quad a \ sin ^ 2 a_2 + b \ sin a_2 + c = 0$

在哪里

$\ Quad \ Quad m = E / B ^ 2$

$\ Quad \ Quad a = m A ^ 2 + D$

$\ quad \ quad b = -2 m A C$

$\ quad \ quad c = m C ^ 2-F$

3球的测地线的连续点上的一个点，该点通过两个点。
该关系将用于在属于3球的2球的任意点上找到纹理坐标和外部法线。让

$\ Quad \ Quad O$ -3球中心

$\ Quad \ Quad A$ -2球的中心

$\ Quad \ Quad B$ 是2球面的任意点

$\ Quad \ Quad C$ -期望点位于大地测量线上

$AB$ 在小角度距离

$\ delta$ 从点

$B$

$\ Quad \ Quad D$ -线的交点

$AB$ 和

$OC$

$\ Quad \ Quad E$ -穿过点的线的交点

$D$ 垂直于直线

$AB$ 和一条线穿过一个点

$O$ 平行于直线

$AB$

$\ Quad \ Quad r_a$ -2球的角半径

$\ Quad \ Quad a =（\ pi-r_a）/ 2$

$\ Quad \ Quad b = a-\ delta$
如果

$r_a> \ pi$ 那应该放

$r_a = 2 \ pi-r_a$ 和

$\ delta =-\ delta$
会发现

$\ vec {OD}$

$\ quad \ quad \ vec {OD} = \ vec {OA} + \ vec {AB} / | \ vec {AB} | \ cdot | \ vec {AD} |$

在哪里

$\ quad \ quad | \ vec {AD} | = | \ vec {AB} | / 2 + | \ vec {OE} |$

$\ quad \ quad | \ vec {OE} | = | \ vec {DE} | / \棕褐色$

$\ quad \ quad | \ vec {DE} | = R \罪$

会发现

$\ vec {OC}$

$\ quad \ quad \ vec {OC} = \ vec {OD} / | \ vec {OD} | \ cdot R$

灯饰

我们将使用两种照明模型。

简单的照明模型。 在此模型中，表面点的亮度取决于表面的外部法线与观察者的方向之间的角度的余弦值。我们将在为说明材料构造图像时使用它。实际上，这是一个点光源位于观察者所在位置的模型，其中，表面点的亮度不取决于与光源的距离。

逼真的照明模型。 该模型将具有专用的点光源。我们将在构建逼真的图像时使用它。该模型可以考虑波前区域对表面点亮度的影响（实际上是到光源的距离的影响）。在具有球形几何形状的封闭宇宙中，波前面积与球的条件半径的平方成正比，而测地线半径等于从曲面点到光源的距离。随着距光源距离的增加，到赤道的波前面积增加（光线发散），在赤道减小之后（光线会聚，聚焦）。通过与“宇宙中心”相对的点之后，发生相反的过程：光线首先发散，然后再次会聚。此外，该模型可以考虑感知特性（韦伯-费希纳定律）。

为了构建图像，我们将使用反向光线跟踪。为了使模型具有交互性（我们将检查世界并在其中移动），必须实时构建图像。因此，我们将在片段着色器中执行计算（我们使用WebGL）。我们用JavaScript实现该接口。

贴图

从这里纹理Earth.jpg

从这里纹理moon.jpg

从这里纹理sun.png

初次相识

我们将创建一个测地线长度为100的三维封闭世界-因此对我们来说更容易导航-我们的世界赤道将位于距离25（测地线长度的四分之一）处，而与地球相对的极点位于距离50（测地线长度的一半）处。我们将一个行星放置在我们的世界中，并根据其所属的八分圆数将其表面的某些部分涂上颜色：

Octant	X标志	Y标志	Z标志	色泽
我	+	+	+	红色（ R ed）
II	--	+	+	绿色（绿色）
三级	--	--	+	蓝色（ B lue）
IV	+	--	+	橘色
V	+	+	--	蓝色（ C yan）
六	--	+	--	紫色（ M agenta）
七	--	--	--	黄色（黄色）
八	+	--	--	白

作为主要纹理，我们将使用3x6棋盘的纹理，也就是说，每个平行和子午线将恰好经过12个像元。作为替代纹理，我们将使用地球的纹理。下面是我们这个星球熟悉飞行的照片。

北极快照。 X轴指向右侧，Y轴指向上方，Z轴指向我们。应用替代纹理时，您可以看到：

右边是太平洋
以上-北美
左-大西洋
底部-欧亚大陆

从北极到赤道以及从赤道到南极的飞行照片。

南极快照。 X轴指向右侧，Y轴向下，Z轴远离我们。应用替代纹理时，您可以看到：

右-太平洋，新西兰，澳大利亚
从上面-印度洋
左-非洲大西洋
底部-南美洲

视觉研究

我们将对我们的世界进行视觉研究，以发现与我们在二维封闭世界中发现的效应类似的事物。

双打。 就像在二维模拟中一样，我们世界上的每个身体都会有一个双重物体-如果我们看到北极摆在我们面前，那么转身就可以看到……南极。由于我们离行星足够近，所以双星表面的收缩很明显。

观察者远离行星移动的实验 （每个图像左上角的数字是观察者与行星之间的距离）。

可以看出：

最初，行星的角大小减小-这是通常的直接透视图
然后，当行星经过我们世界的赤道（距离超过25）时，其角大小会增加-这是我们熟悉的相反视角的影响
爬到世界的另一极时，我们看到了一个狭窄的表面（距离46.875）
当行星位于我们世界的另一极（距离50）时，它延伸到整个天空
从世界的另一端滑动时，我们看到了一个拉伸的表面（距离53.125）
行星经过我们世界的另一极后，它看起来是对称变换的-红色八分位变了蓝色，依此类推
然后，行星的角大小减小（从50到75的距离），然后增大（从75到100的距离）-这是第二个正向和反向透视的熟悉效果

人工制品。 使用该模型时，注意到在行星经过观察者位于25、50和75距离处的点的过程中，可能会出现伪影-头发可能“生长”在行星上，甚至可能“破碎”。显然我的数学没有考虑到某些因素）

行星在我们世界另一极附近的图片 （使用了广角“镜头”）。我们面前的行星表面非常狭窄-您不仅可以看到整个北半球，而且可以看到赤道后面的南半球的一部分。我们身后的行星表面非常伸展-南极清晰可见。两个表面彼此相对延伸，试图将我们包围在球形壳中，并向我们展示行星在天空中延伸的图片。

观察者仰视的实验 （每张图片左上角的数字是向下方向与凝视之间的角度）。

在图片中：

首先出现在我们这星球的地平线上
然后，我们在其上方看到第二个地平线，在这里我们找到了位于我们这一星球后面背后我们星球一侧的东西
仰望，我们看到了地球的背面

双水平图像 （使用广角“镜头”）。天空带足够大，因为我们处于大约50公里的高度。

头部上方的天空图片 （使用了广角“镜头”）。

没有夜晚的世界。
此外，为简单起见，我们将地球称为地球，其自然卫星-月亮，以及绕其旋转的恒星-太阳。为了清楚起见，将不会观察到太阳，地球，月球及其轨道的大小比例。
图中：穿过大西洋的白天和黑夜之间的边界。同时，不断缩小和成长的地球是可见的。坐在我们世界月球基地上的家伙看到的照片大致相似）

关于动画：地球白天和黑夜之间边界的移动。您可以看到太阳盘与太阳盘的重叠部分，这是太阳盘沿长路径释放的光线所照亮的。

日食和月食。
图为：月亮从地球的阴影中出现。可见地球和月球白天和黑夜之间的边界。

在动画上：日食和月食。

可以看出：

首先，地球在月亮上投下阴影，月亮在地球上投下阴影
然后月亮从地球的阴影中出来，月亮的阴影离开了地球的表面
然后月亮的影子回到地球的表面，月亮又进入了地球的影子
当月球被地球的圆盘覆盖时，月亮的白天和黑夜之间的边界是不可见的，因为面对我们的月亮一侧仍在地球的阴影下

动画方面：地球与月球在白天和夜晚之间的边界移动以及日食和月食。在我们世界的拉格朗日点 L _2上为天文台服务的人看到的照片大致相同）（当然，如果我们忽略了地球自转）

图：世界上国际空间站的曙光）

结论

这都是为了什么？我只是真的想通过一个生活在球形几何形状的紧凑封闭宇宙中的生物的眼睛看世界。要了解这个没有Christoffel符号和类似事物的美好世界，同时又要保留在高等数学课程的框架内。结果就在您眼前。一切似乎都解决了。希望您度过了愉快而愉快的一天！

源代码。

工作模型（在PC上打开，不适用于移动设备）。

对于那些对此主题感兴趣的人，有一篇宏伟的文章，讨论了在真实的宇宙中可以观察到的惊人现象：如何绘制黑洞。弯曲时空中的测地线追踪。

三维超球体的世界。 具有球形几何形状的封闭宇宙中的测地线追踪

引言 二维封闭世界

三维封闭世界

型号

初次相识

视觉研究

结论

More articles:

三维超球体的世界。具有球形几何形状的封闭宇宙中的测地线追踪

引言二维封闭世界