后勤行动，单独收集可回收物品

而不是加入

俄罗斯对废物收集和处理的流程进行了完全调整后，这很难说，但我现在不想参与垃圾填埋场的补充。 因此，在许多大城市，以一种方式或另一种方式，都有志愿人员进行特别收集的运动。

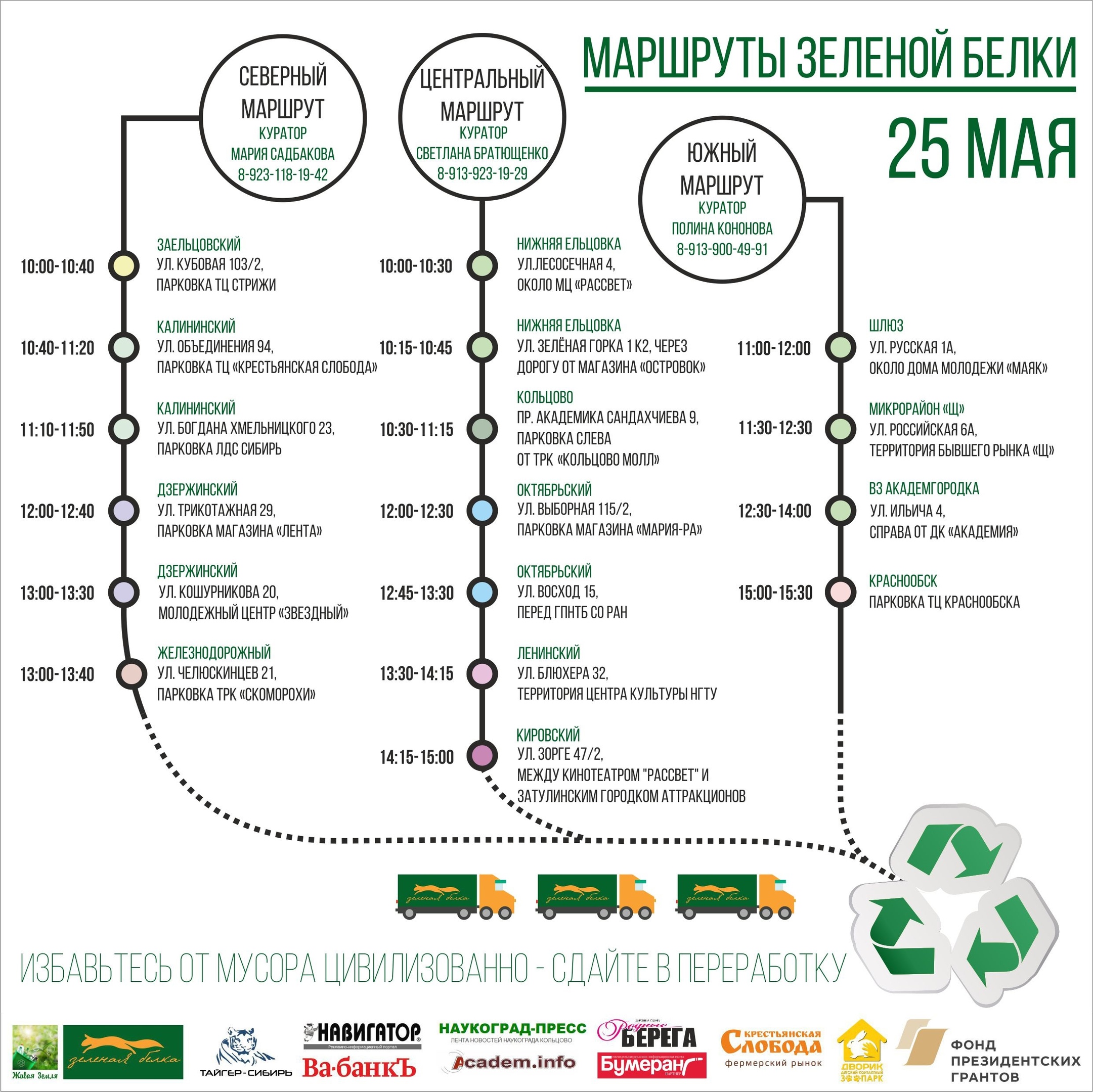
在新西伯利亚，这种活动是在“绿色松鼠”运动的周围开展的，在该框架下，每月一次，关注环境的城市居民在特定时间将积累的可回收家庭垃圾带到预定的地方。 同时，一辆租来的卡车到达那里，将收集和分类的可回收材料带到现场，从那里在各种加工企业之间重新分配。 该行动自2014年以来一直存在，自那时以来，可回收物的收集点数量及其数量都大大增加了。 对于卡车路线选择而言，仅仅注视是不够的，我们开始开发优化模型以最小化运输成本。 这些模型中的第一个是本文的主题。

在第1部分中，我将详细说明并举例说明组织行动的方案。 此外，在第2节中，将运输成本最小化的任务正式化为使用时间窗解决异构车辆车队车辆路由问题的任务。 第3节专门使用自由分布的软件包来解决此问题，以解决混合整数线性数学编程问题GLPK。

1.动作“绿松鼠”

自2014年以来，“ 生命地球”倡议小组每月进行一次活动，以分离新西伯利亚回收的绿色松鼠的收藏。 在撰写本文时，已接受了一些保留，包括标签为PET，PE，PP，PS，玻璃，铝，铁，家用电器，废纸等的废塑料被回收。 50多名志愿者参加了行动的准备和实施。 该诉讼不是商业性的，参与是免费的，并不意味着金钱上的回报。

点数

行动在城市的17个地点举行，彼此之间的距离为15分钟至90分钟，汽车被汽车覆盖。 照片中的这些要点之一：左边是沿着墙壁收集各种塑料碎片的袋子，右边是一辆卡车，将来要装载所有东西，而右边是一个有耳朵的志愿者。



此时的所有活动都是由策展人组织的，他们对准备好履行职责的时间有限制。 在计划一个动作时，策展人报告在该时间点动作必须经过的时间间隔。

在每个点上也有关于可回收材料平均收集量的数据。

路线

点被组织成由卡车连续驱动的路线。 卡车的行驶由路线负责人监控，路线负责人监视操作环境并做出处理特殊事件的决定。



货车

在按小时计算的货车运输建议框架内共同租赁。 无法将塑料压紧到位，因此，表征卡车的主要参数是车身的体积。 在我们的情况下，承载能力不是限制因素。

这项行动的主要费用与支付卡车租金有关，因此，减少这一行动对于我们份额的存在和发展至关重要，从形成负责任的消费观念的意义上说，这一点具有制度上的意义。 接下来，将基于离散优化方法的应用，即数学编程，描述解决该问题的方法。

2.形式化

在构建数学模型时，我们将停留在线性混合整数程序的框架内，对于该程序而言，了解7类代数的知识就足够了。

唯一的困难可以与在公式中使用抽象符号和求和符号相关联。 我希望这不会吓跑那些很少接触数学课本的读者。

在优化模型中，可以区分四个组件：

• 形成单独路线的点组的形成；
• 为每个组定义一个绕道方案；
• 满足卡车到达每个时间点的要求；
• 确定服务每条路线所需的卡车类型。

我们考虑每个部分，并在必要时引入必要的符号。

点分组

让 $$$V = \ {1，\点，n \}$ 有很多可回收材料的收集点索引，然后将收集的可回收材料运到的地点（我们称为仓库 ）的索引为0。 $$$\ bar {V} = V \ cup \ {0 \}$

每组点形成一条单独的路线。 通过 $$$R$ 表示路线号的集合。

让数量 $$$z_ {ir}，i \ in I，r \ in R$ 如果点等于1 $$$我$ 包含在路线中的数字 $$，否则为零。 然后要求点 $$$i \ in V$ 必须输入其中一条路线可以写为

$$

$$\ sum_ {r \ in R} z_ {ir} = z_ {i1} + z_ {i2} + \点+ z_ {in} =1。$$

仓库必须输入所有路线： $$$z_ {0r} = 1，r \ in R$


绕行的定义

路线是点和交叉点之间的交替序列。 形式上，它们都始于集合的某一点 $$$V$ 并在仓库中结束，但是，假设所有路线都是循环的将更容易。 这种假设不会改变本质，但会使所有顶点相同：在这种情况下，没有最终顶点，它们都是过渡的。

积分 $$$i，j \ in \ bar {V}$ 和路线 $$$r \在R $$ 设置一个变量 $$$x_ {ijr}$ 如果在带数字的路线中等于1 $$卡车从点移动 $$$我$ 到这一点 $$$j$ ，否则为零。

然后我们首先要求卡车沿着路线行驶 $$$r \在R $$ 参观了要点 $$$i \ in V$ 如果她分成几组然后按数字落入该组 $$：

$$

$$\ sum_ {j \ in \ bar {V}} x_ {jir} = z_ {ir}，\ quad i \ in \ bar {V}，r \ in R$$

其次，卡车到达终点后 $$$i \ in \ bar {V}$ 必须离开她。

$$

$$\ sum_ {j \ in \ bar {V}} x_ {jir} = \ sum_ {j \ in \ bar {V}} x_ {ijr}，\ quad i \ in \ bar {V}，r \ in R$$

您可能会注意到，这些限制允许数量 $$$x_ {ijr}$ 定义一组不相交的回路的路由。 当然，这种路线是没有意义的，为避免这种情况需要采取一些限制措施。


满足卡车到达各点时的要求

换句话说，您只需要在策展人指示的时间窗口内访问点。 通过 $$$B_i$ 和 $$$E_i$ 分别表示时间点的开始和结束，在该时间间隔中，点的管理者 $$$我$ 可以参加。

为了跟踪这些限制的执行情况，我们需要有关卡车在路线上的停靠站和过路处所花费的时间的信息。 通过 $$$L_i，i \ in V$ 表示该点的加载持续时间 $$$我$ ，并通过 $$$D_ {ij}，i，j \ in \ bar {V}$ -从一点移动的时间 $$$我$ 到这一点 $$$j$ 我们预订 $$$D_ {0i} = 0$ 对于所有 $$$i \ in \ bar {V}$ ，通常可以执行 $$$D_ {ij} \ neq D_ {ji}$ 对于任何 $$$i \ neq j$

我们介绍非负变量 $$$a_i，i \ in \ bar {V}$ 和 $$$w_ {ir}，i \ in \ bar {V}，r \ in R$ 等于该点的到达时间和等待时间 $$$我$ 沿路线行驶时 $$，分别。 对于输入的值，应满足以下关系。

等待时间不能少于加载所需的时间

$$

$$w_ {ir} \ geq L_iz_ {ir}，\ quad i \ in \ bar {V}，r \ in R，$$

如果该点不属于路线，则等于零 $$

$$

$$w_ {ir} \ leq Mz_ {ir}，\ quad i \ in \ bar {V}，r \ in R，$$

到达时间 $$$j$ 在适当的时间为上一点计算 $$$我$ 这是一个相当大的常数 $$$M$ 用于消除相互之间移动时不必要的依赖性 $$$我$ 和 $$$j$ 没有完成。

$$

$$a_i + \ sum_ {r \ in R} w_ {ir} + D_ {ij} \ leq a_j + M（1-\ sum_ {r \ in R} x_ {ijr}），\ quad i \ in I，j \在V中，$$

卡车的进出必须在馆长指定的间隔内。

$$

$$a_i \ geq B_i，\ quad i \ in V，$$

$$

$$a_i + \ sum_ {r \ in R} w_ {ir} \ leq E_i，\ quad i \ in V.$$

确定维修每条路线所需的卡车类型
表示以下类型的可供出租的卡车： $$$T$ 卡车类型 $$$t \ in T$ 以身体体积为特征 $$$C_t$ 一小时的租金 $$$P_t$ 最小卡车租赁时间 $$$t$ 用...表示 $$$U_t ^ 0$ 该点收集的可回收物数量 $$$i \ in V$ 用...表示 $$$G_i$

我们介绍变量 $$$y_ {tr}，t \ in T，r \ in R$ 如果卡车类型等于1 $$$t$ 用编号分配给服务路线 $$，否则为零。

整数变量 $$$u_ {tr}，t \ in T，r \ in R$ 设置租用卡车类型的时间 $$$t$ 用号码服务路线 $$
对于每条路线， $$$r \在R $$ ，您必须指定卡车的类型：

$$

$$\ sum_ {t \ in T} y_ {tr} = 1，\ quad r \ in R$$

根据路线之间的点的细分，某些路线可能变得微不足道，即仅包含仓库。 如果路线 $$不平凡，那么至少要租用分配给它的卡车 $$$U_t ^ 0$ 小时。

$$

$$u_ {tr} \ geq U_t ^ 0（y_ {tr}-\ sum_ {i \ in V} z_ {ir}），\ quad t \ in T，r \ in R$$

同时，租约的期限也应超过停车和沿路线行驶的总期限。

$$

$$u_ {tr} \ geq \ sum_ {i \ in V} \ sum_ {j \ in \ bar {V}} D_ {ij} x_ {ijr} + \ sum_ {i \ in \ bar {V}} w_ { ir} -M（1-y_ {tr}），\ quad r \ in R，t \ in T.$$

添加限制以提供以下属性：如果卡车是类型的 $$$t$ 未分配给路线 $$，其租用时间为零。

$$

$$u_ {tr} \ leq My_ {tr}$$

在路线点收集的所有可回收物品应装在卡车的后部。

$$

$$\ sum_ {i \ in V} G_iz_ {ir} \ leq \ sum_ {t \ in T} C_ty_ {tr}，\ quad r \ in R.$$

最后，我们的目标是最大程度地减少卡车的租赁费用，使用引入的名称写成： $$$\ sum_ {t \ in T} \ sum_ {r \ in R} P_tu_ {tr}$

寻找解决方案

容易验证优化模型中涉及的所有表达式都是变量的线性函数，因此，要找到精确和近似的解决方案，可以使用标准包来解决混合整数编程问题，例如Gurobi ， CPLEX ， Xpress ， ORtools ， SCIP ， BLIS等
我们使用GMPL语言编写了一个模型，以最小化运输成本。 这将使我们能够使用免费的GLPK软件包来实现我们的目的。 要编写代码和调试模型，可以方便地下载GUSEK开发环境 ，该环境已包含GLPK。

古瑟克看起来像这样：



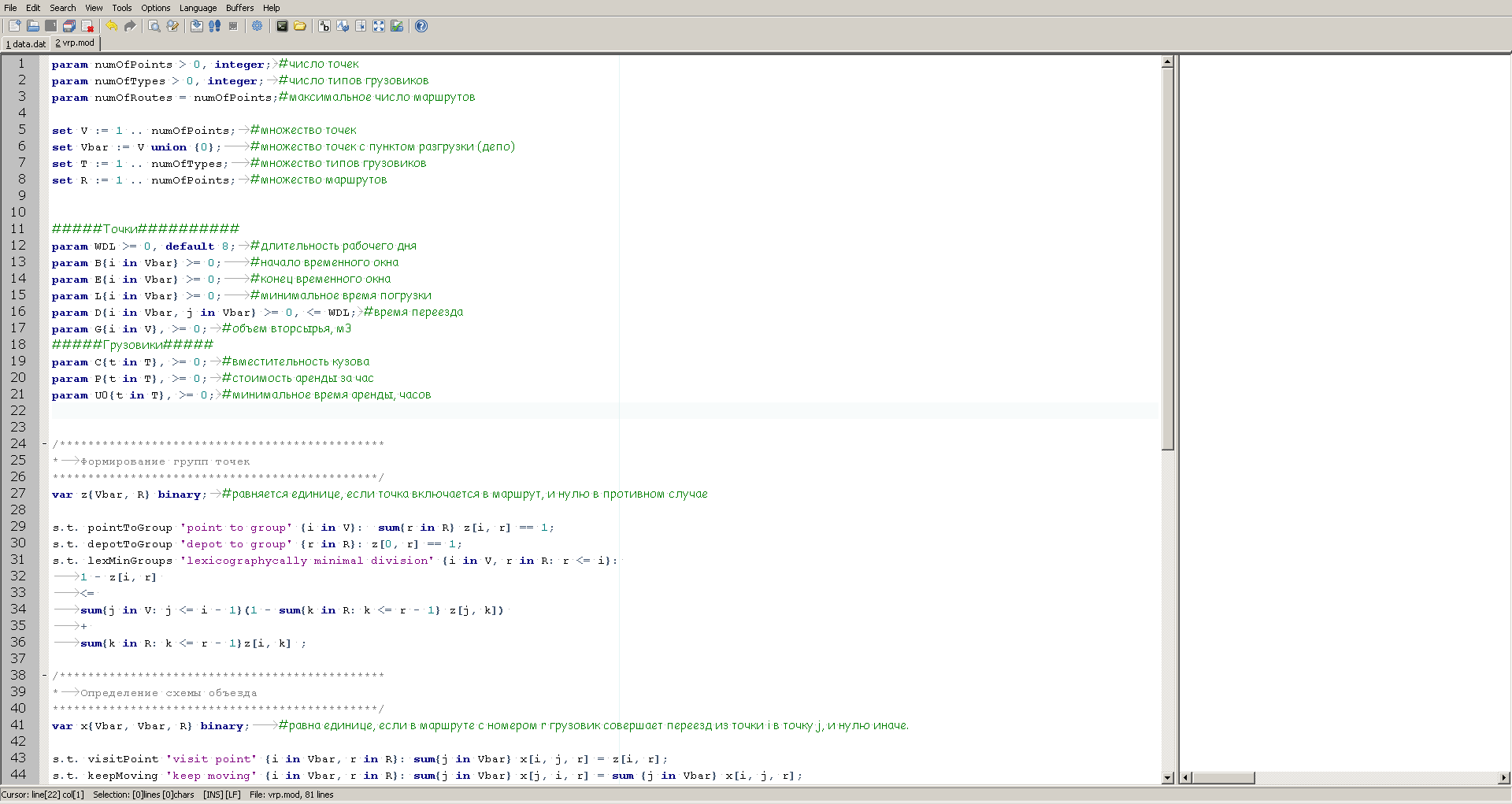
左边是模型的描述，右边是显示计算进度信息的窗口，求解器将在启动后提供该窗口。


为了快速入门，我还将添加准备好用于模型的头部数据：


将模型代码复制到名称为例如model.mod的文件并将输入数据复制到data.dat文件后，一切就绪。 我们将计算时间设置为100秒（使用键--tmlim [以秒为单位的时间]完成），使用输入数据将路径传输到文件（使用键-d [文件路径]），



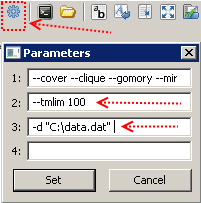
然后按F5。 如果成功，则会在右侧窗口中显示消息，并且一百秒钟后，我们将获得GLPK在分配的时间内设法找到的最佳解决方案。



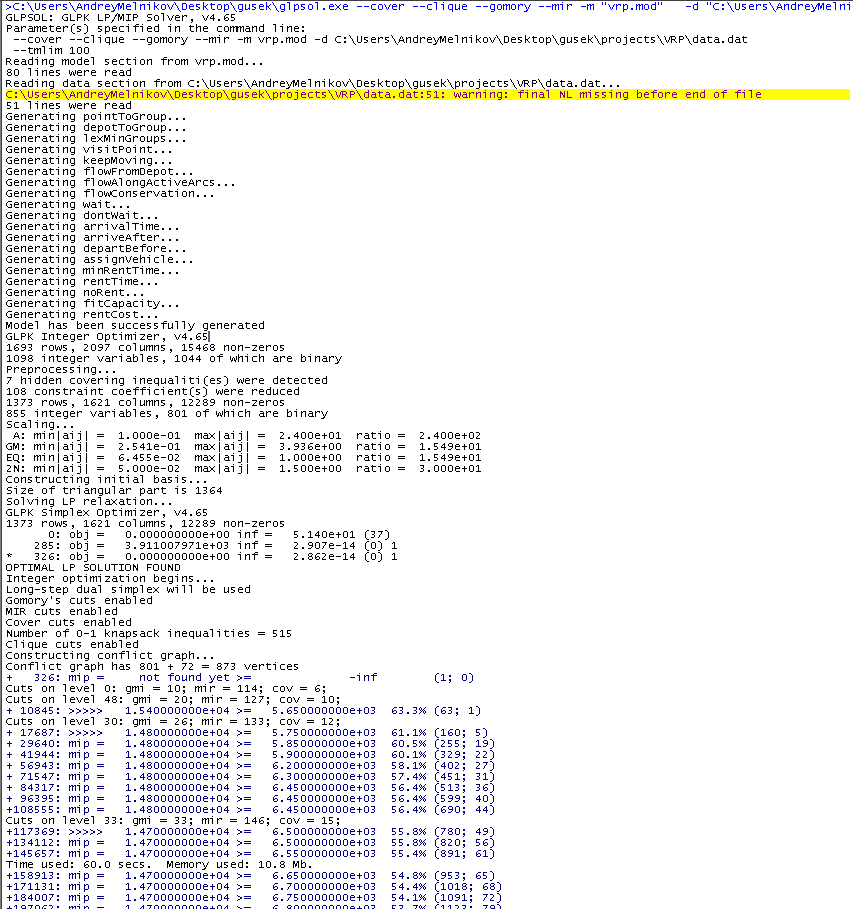
在蓝色文本中，我们对铭文“ mip =”之后的含义感兴趣。 如您所见，它不时减少。 所有新的解决方案都在工作中，此栏中显示了最多的运输成本值（到目前为止有14700个）。 下一个数字是现有最佳解决方案的下限。 最初，估计值被大大低估了，但是随着时间的推移而完善，即增加。 左右两边的值在收敛，截屏时它们之间的相对差距为54.1％。 一旦该数字变为零，该算法将证明找到的最佳解决方案是最佳解决方案。 在实践中并不总是需要等待此事件的合理性，这不仅是因为时间长，而且重要的是要保留一个好的解决方案，这通常是相对较快的解决方案，并且主要时间成本与证明最佳可能所需的估计值有关。

而不是结论

路由问题的计算极其复杂，并且随着需要访问的点数的增加，求解器找到解决方案并证明其最优性所需的时间正在迅速增长。 但是，对于相当小的示例，在合理的时间内，求解器能够构建成功的路线集，并可用于支持决策。 对模型提出的工艺路线选项的分析帮助我们发现了降低成本的重要机会，这对于库存的存在和发展至关重要。

我们的进一步努力是在工作地点收集可回收物的数量不确定的情况下进行的。 我们正在开发许多随机编程模型，以制定卡车路线规划中的战略和运营决策。 如果这个话题最终引起人们的关注并引起人们的兴趣，我也将写这篇文章，因为不久我们所有人都将不得不更加彻底地深入研究环境问题，这就是我们希望我们取得成功的原因。