让我们进行一些可能发生某些事件的抽象实验。 该实验进行了五次,其中四次发生了相同的事件。 从这4/5可以得出什么结论?

有
一个伯努利公式可以给出答案,即在已知的初始概率下,五分之四的概率出现。 但这没有给出答案,如果事件被证明是5分之4,那么最初的概率是多少。让我们撇开伯努利公式。
我们将创建一个简单的小型程序,以模拟这种情况下的概率过程,并基于计算结果构造一个图形。
void test1() { uint sz_ar_events = 50;
该程序的代码以及辅助功能可在
此处找到。
计算结果被放入Excel并制定了时间表。

该图的这种形式可以称为概率值的概率密度分布。 它的面积等于在此土墩中分布的单位。
为了使图片更完整,我将提到该图对应于根据概率参数的伯努利公式得出的图,再乘以N +1个实验次数。
此外,在本文中,我在文章中使用k / n形式的小数,这不是除法,而是n次实验中的k个事件,以免每次都不从n中写入k。
下一个 可以增加实验次数,并获得概率值主要值所在位置的较窄区域,但是无论如何增大,该区域都不会以众所周知的概率减小到零区域。
下图显示了4 / 5、7 / 9、11 / 14和24/30的分布。 面积越窄,土墩越高,其面积是一个恒定的单位。 选择这些关系是因为它们都约为0.8,而不是因为这些关系可能以初始概率的0.8出现。 选择该参数以证明即使进行了30次实验,仍可能存在哪些值范围。
该图的程序代码
在这里 。

由此可以得出结论,实际上无法精确确定实验概率,但是我们只能假设该数量可能位置的区域,其准确度取决于进行了几次测量。
无论进行多少次实验,初始概率始终可能分别为0.0001和0.9999。 为简单起见,将丢弃极不可能的值。 例如,我们以分发计划主要区域的95%为例。
这样的事情称为置信区间。 我还没有就应该留下多少利息以及为什么要留下利息提出任何建议。 为了减少天气预报,需要发射更多的航天飞机。 他们通常也没有提到仍然将哪个置信区间用于事件的概率以及是否使用了该置信区间。
在我的程序中,在
此执行置信区间边界的计算。
事实证明,该事件的概率由概率值的概率密度确定,并且仍然有必要在其上施加主要值区域的一定百分比,以便您至少可以明确地说出正在研究的事件是哪种概率。
现在,关于一个更真实的实验。
让每个人都对硬币感到无聊,扔掉这个硬币,然后从尾巴上的5滴中抽出4滴-这是非常真实的情况。 实际上,这与前面所描述的不太一样。 这与之前的实验有何不同?
先前的实验是在事件概率可以在0到1的间隔内平均分配的前提下进行描述的
。 。 但是没有硬币掉落的可能性,例如0.1或0.9总是在一侧。
如果您从普通硬币到最弯曲的硬币上取一千种不同的硬币,然后将它们抛掷一千次或更多次来衡量损失,那么它将表明它们确实从0.4到0.6的范围内掉了下来(这些是随机数,我不会但我要找出1000个硬币,然后每扔1000次)。
这个事实如何改变模拟一个特定硬币的概率的程序,对于该硬币,接收到5个尾巴中的4个?
假设硬币的一侧损失分布被描述为参数均值= 0.5,标准偏差= 0.1时正态分布图的近似值。 (在下图中,它以黑色显示)。
在程序中,当根据指定规则将初始概率的生成从等分分布更改为等分分布时,将得到以下图形:
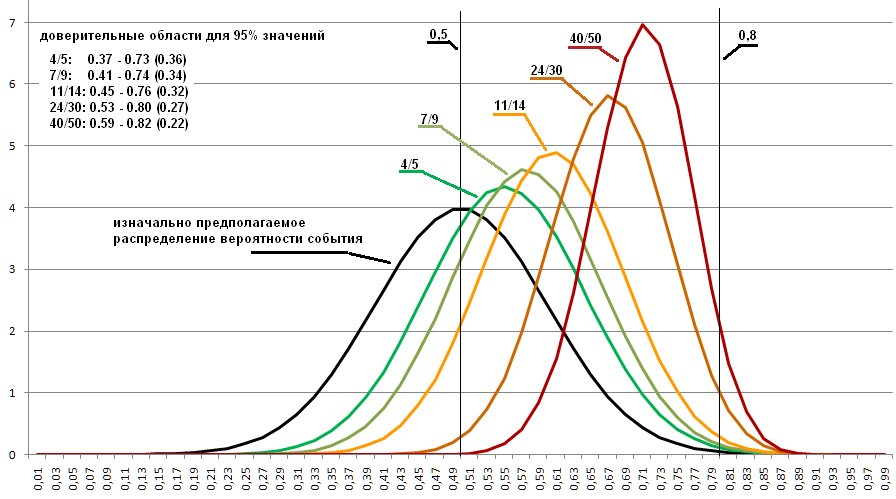
此选项的代码
在此处 。
可以看出,分布发生了很大的变化,现在确定了一个稍微不同的区域,在该区域中很有可能达到所需的概率。 因此,如果知道这些事物存在什么概率(我们要测量其中一种概率),则可以在某种程度上改善结果。
结果,4/5并不意味着什么,甚至进行的50个实验也不是很有用。 这是很少的信息,无法确定哪种概率仍然是实验的基础。
==更新==
正如
jzha在评论中提到的那样,一个非常了解数学的人,也可以使用精确的公式来构造这些图。 但是,本文的目的仍然是尽可能清晰地展示每个人如何称呼概率。
为了使用精确的公式进行构建,有必要通过beta分布的近似值考虑所有硬币的概率分布的可用数据,并通过计算分布,已经进行了计算。 这样的方案对如何执行此操作有大量的解释,如果我在这里进行描述,它将变成一篇有关数学计算的文章,而不是日常概率。
如何用硬币描述公式的特殊情况,请参见
jzha的评论。