🐷 🙏🏼 👩🏻‍🔧 如何在ClickHouse中加快LZ4解压缩？ 💌 👨🏻‍✈️ ⬛️

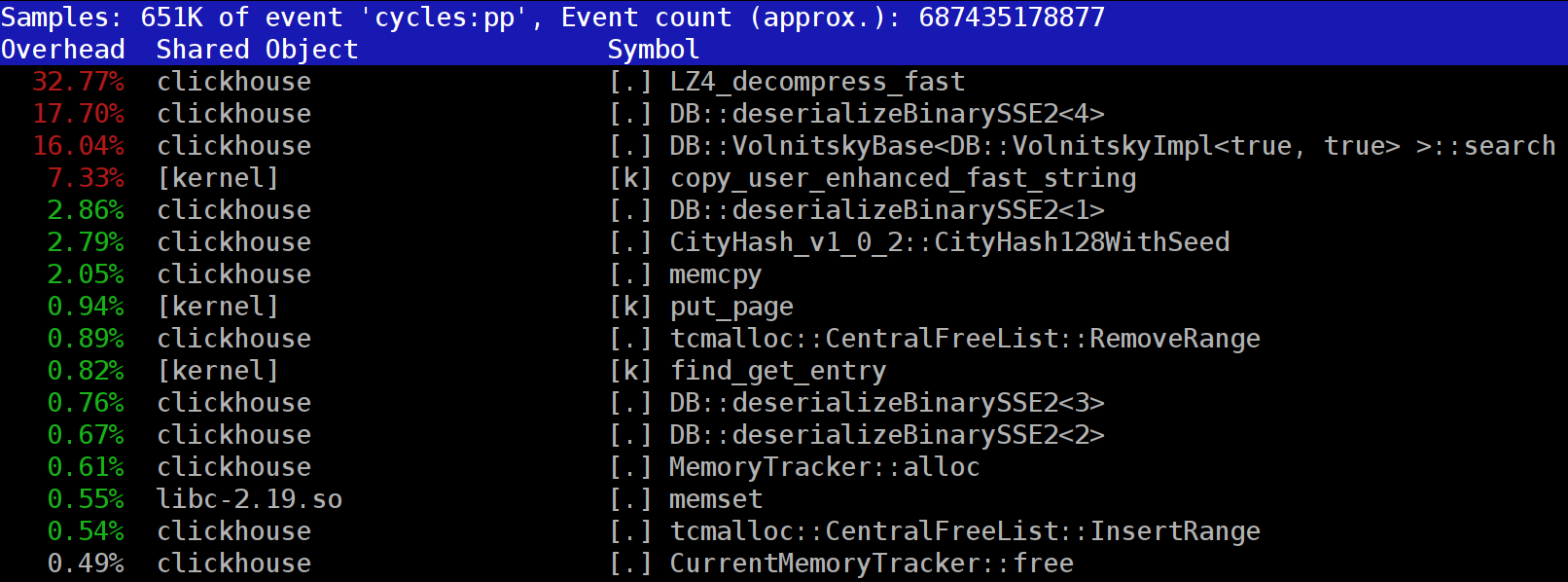
在ClickHouse中运行查询时，您可能会注意到分析器经常在顶部附近显示LZ_decompress_fast函数。这是怎么回事？这个问题使我们想知道如何选择最佳的压缩算法。

ClickHouse以压缩形式存储数据。在运行查询时，ClickHouse尝试尽可能少地做，以节省CPU资源。在许多情况下，所有潜在耗时的计算都已经过优化，而且用户编写了经过深思熟虑的查询。然后剩下要做的就是执行减压。

那么，为什么LZ4减压会成为瓶颈？ LZ4似乎是一种非常轻巧的算法：每个处理器内核的数据解压缩速率通常为1-3 GB / s，具体取决于数据。这比典型的磁盘子系统快得多。此外，我们使用所有可用的CPU内核，并且解压缩在所有物理内核上线性扩展。

但是，有两点需要牢记。首先，从磁盘读取压缩数据，但是解压缩速度是根据未压缩数据的数量给出的。如果压缩率足够大，则几乎没有任何内容可以从磁盘读取。但是会有很多解压缩的数据，这自然会影响CPU利用率：对于LZ4，解压缩数据所需的工作量几乎与解压缩数据本身的大小成正比。

其次，如果缓存了数据，则可能根本不需要从磁盘读取数据。您可以依靠页面缓存或使用自己的缓存。在面向列的数据库中，缓存效率更高，因为只有经常使用的列保留在缓存中。这就是LZ4在CPU负载方面经常成为瓶颈的原因。

这又提出了两个问题。首先，如果解压缩使我们放慢了速度，那么值得一开始压缩数据吗？但是这种推测在实践中是无关紧要的。直到最近，ClickHouse配置仅提供两个数据压缩选项-LZ4和Zstandard 。默认情况下使用LZ4。切换到Zstandard会使压缩更强或更慢。但是没有选择完全禁用压缩，因为假定LZ4提供了可以始终使用的合理的最小压缩。（这正是我爱LZ4的原因。）

但是随后，一个神秘的陌生人出现在国际ClickHouse支持聊天中，他说他有一个非常快的磁盘子系统（带有NVMe SSD），并且解压缩是唯一使他的查询速度变慢的事情，因此能够在没有存储空间的情况下存储数据会很好压缩我回答说我们没有此选项，但是添加起来很容易。几天后，我们收到了一个实现压缩方法none 请求。我要求贡献者报告该选项在多大程度上有助于加快查询速度。对此的回应是，该新功能实际上没有用，因为未压缩的数据开始占用过多的磁盘空间，并且不适合那些NVMe驱动器。

出现的第二个问题是，如果有缓存，为什么不使用它来存储已经解压缩的数据？在许多情况下，这是可行的可能性，它将消除减压的需要。 ClickHouse也具有这样的缓存：解压缩块的缓存。遗憾的是浪费了很多RAM。因此，通常只对使用几乎相同数据的小型顺序查询有意义。

我们的结论是，始终最好以压缩格式存储数据。始终以压缩格式将数据写入磁盘。压缩也可以通过网络传输数据。我认为，即使在10 GB网络中的单个数据中心内传输数据而没有超额订购，默认压缩也是合理的，而在数据中心之间传输未压缩的数据则是不可接受的。

为什么选择LZ4？

为什么选择LZ4？我们不能选择更轻的东西吗？从理论上讲，我们可以，这是一个好主意。但是，让我们看一下LZ4所属的算法类别。

首先，它是通用的，不会适应数据类型。例如，如果您事先知道将有一个整数数组，则可以使用VarInt算法之一，这样可以更有效地使用CPU。其次，LZ4并不过度依赖数据模型假设。假设您有一个有序的传感器值时间序列，是一个浮点数数组。如果考虑到这一点，则可以计算这些数字之间的增量，然后使用通用算法对其进行压缩，这将导致更高的压缩率。

将LZ4与任何字节数组或任何文件一起使用都不会有任何问题。当然，它确实具有专门化（稍后会详细介绍），在某些情况下，它的使用是没有意义的。但是，如果我们将其称为通用算法，我们将非常接近事实。我们应该注意，由于其内部设计，LZ4作为特殊情况自动实现了RLE算法。

但是，更重要的问题是，就整体速度和压缩强度而言，LZ4是否是此类中的最佳算法。最佳算法被称为Pareto边界，这意味着没有其他算法可以以一种方式绝对好，而在其他方式（以及各种各样的数据集）上却不差。一些算法速度更快，但压缩率较小，而其他算法则具有较强的压缩率，但压缩或解压缩速度较慢。

老实说，LZ4并不是真正的帕累托前沿-有一些可用的选项稍微好一点。例如，从绰号为powturbo的开发人员那里查看LZTURBO 。毫无疑问，归功于encode.ru社区（有关数据压缩的最大且唯一的论坛），结果的可靠性也得到了保证。不幸的是，开发人员没有分发源代码或二进制文件；只有少数人可以使用它们进行测试，也可以花很多钱（尽管看起来还没有人为此花钱）。还要看看蜥蜴（以前是LZ5）和密度。当您选择某个压缩级别时，它们可能比LZ4更好。另一个非常有趣的选择是LZSSE 。但请先阅读本文，然后再签出。

lz4如何工作

让我们看一下LZ4的总体工作原理。这是LZ77算法的实现之一。 L和Z代表开发人员的名称（Lempel和Ziv），而77代表该算法于1977年发布。它还具有许多其他实现：QuickLZ，FastLZ，BriefLZ，LZF，LZO以及gzip和zip（如果使用了低压缩级别）。

使用LZ4压缩的数据块包含两种类型的条目序列（命令或指令）：

文字：“将以下N个字节保持原样并将其复制到结果中”。
匹配：“从解压缩结果中取N个字节，起始于相对于当前位置的偏移值”。

例子压缩前：

 Hello world Hello

压缩后：

 literals 12 "Hello world " match 5 12

如果我们在执行这些命令时获取一个压缩块并遍历游标，则将得到原始的未压缩数据。

因此，基本上这就是数据解压缩的方式。基本思想很明确：为了执行压缩，该算法使用匹配对重复的字节序列进行编码。

一些特征也很清楚。这种面向字节的算法不会剖析单个字节。它只会完整复制它们。这就是它与熵编码的不同之处。例如， zstd是LZ77和熵编码的组合。

请注意，压缩块的大小不应太大。选择大小以避免在解压缩期间浪费大量RAM，避免在压缩文件（包含大量压缩块）中降低随机访问速度，并且有时使块适合CPU缓存。例如，您可以选择64 KB，以便压缩和未压缩数据的缓冲区将适合L2高速缓存，其中一半仍然可用。

如果需要压缩更大的文件，则可以串联压缩的块。这对于在每个压缩块中存储其他数据（例如校验和）也很方便。

匹配的最大偏移量是有限的。在LZ4中，限制为64 KB。该数量称为滑动窗口。这意味着可以在光标之前的64 KB窗口中找到匹配项，该窗口随光标向前移动而滑动。

现在让我们看一下如何压缩数据，或者换句话说，如何在文件中找到匹配的序列。您可以始终使用后缀trie（如果您真的听说过，那就太好了）。有一些方法可以确保最长的匹配项在压缩后位于前面的字节中。这称为最佳解析，它为固定格式的压缩块提供了几乎最佳的压缩率。但是有更好的方法，例如找到不一定足够长的足够好的匹配。找到它的最有效方法是使用哈希表。

为此，我们迭代游标遍历原始数据块，并在游标之后占用几个字节（比方说4个字节）。我们对它们进行哈希处理，然后将距块开头（从中取出4个字节）的偏移量放入哈希表中。值4称为“最小匹配”-使用此哈希表，我们可以找到至少4个字节的匹配项。

如果我们查看哈希表并且该哈希表已经有匹配的记录，并且偏移量不超过滑动窗口，我们将检查以查看在这4个字节之后还有多少个字节匹配。也许还有更多的比赛。哈希表中也可能有冲突，但没有匹配项，但这不是什么大问题。您可以将哈希表中的值替换为新值。哈希表中的冲突只会导致较低的压缩率，因为匹配项会更少。顺便说一句，这种类型的哈希表（具有固定的大小，没有冲突的解决方案）称为“缓存表”。这个名称很有意义，因为在发生冲突的情况下，缓存表只会忘记旧条目。

细心的读者面临的挑战。假设数据是小尾数格式的UInt32数字数组，表示自然数序列的一部分：0、1、2 ...说明为什么使用LZ4时不压缩此数据（压缩数据的大小）与未压缩的数据相比没有任何缩小）。

如何加快一切

所以我想加快LZ4的减压速度。让我们看看减压循环的样子。这是伪代码：

 while (...) {    read(input_pos, literal_length, match_length);    copy(output_pos, input_pos, literal_length);    output_pos += literal_length;    read(input_pos, match_offset);    copy(output_pos, output_pos - match_offset,        match_length);    output_pos += match_length; }

LZ4格式的设计目的是使文字和匹配项在压缩文件中交替出现。显然，字面量总是第一位的（因为从一开始就没有地方可以进行比赛）。因此，它们的长度被一起编码。

实际上，这要复杂得多。从文件中读取一个字节，然后将其分成两个半字节（半字节），其中包含0到15的编码数字。如果相应的数字不是15，则假定为文字长度和匹配项，分别。如果为15，则长度更长，并在以下字节中进行编码。然后读取下一个字节，并将其值添加到长度中。如果等于255，则对下一个字节执行相同的操作。

请注意，LZ4格式的最大压缩率未达到255。另一个无用的观察是，如果您的数据非常冗余，则两次使用LZ4会提高压缩率。

当我们读取文字的长度（然后是匹配长度和匹配偏移量）时，仅复制两个内存块就足以将其解压缩。

如何复制内存块

似乎您只能使用memcpy函数，该函数旨在复制内存块。但这不是最佳方法，也不是真正合适的方法。

使用memcpy并不是最佳选择，因为：

它通常位于libc库中（并且libc库通常是动态链接的，因此将通过PLT间接进行memcpy调用）。
如果在编译时不知道size参数，则编译器不会内联它。
它花费了大量精力来正确处理不是机器字长或寄存器倍数的存储块的剩余数据。

最后一点是最重要的。假设我们要求memcpy函数精确复制5个字节。使用两个movq指令立即复制8个字节，将是很好的选择。

Hello world Hello wo ...
^^^^^ ^^^ - src
^^^^^ ^^^ - dst

但是接下来我们将复制三个额外的字节，因此我们将在缓冲区范围之外进行写入。 memcpy函数无权执行此操作，因为它可能会覆盖程序中的某些数据并导致内存重载错误。而且，如果我们写入未对齐的地址，这些额外的字节可能会落在虚拟内存的未分配页面上或没有写访问权的页面上。这将给我们带来细分错误（这很好）。

但是在我们的情况下，我们几乎总是可以写入额外的字节。我们可以读取输入缓冲区中的额外字节，只要额外字节完全位于其中即可。在相同条件下，我们可以将多余的字节写入输出缓冲区，因为在下一次迭代时仍将覆盖它们。

LZ4的原始实现中已经存在此优化：

 inline void copy8(UInt8 * dst, const UInt8 * src) {    memcpy(dst, src, 8); /// Note that memcpy isn't actually called here. } inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy8(dst, src);        dst += 8;        src += 8;    } while (dst < dst_end); }

要利用这种优化，我们只需要确保距离缓冲区边界足够远即可。这不应该花任何钱，因为我们已经在检查缓冲区溢出。处理最后几个字节，即“剩余”数据，可以在主循环之后完成。

但是，仍然存在一些细微差别。复制在循环中发生两次：带有文字和匹配项。但是，当使用LZ4_decompress_fast函数（而不是LZ4_decompress_safe ）时，当我们需要复制文字时，检查仅执行一次。复制匹配项时不执行检查，但是LZ4格式的规范中有一些条件可以让您避免：

最后5个字节始终是文字。
最后的匹配必须在块结束之前至少12个字节开始。
因此，少于13个字节的块无法压缩。

特殊选择的输入数据可能会导致内存损坏。如果使用LZ4_decompress_fast函数，则需要保护以防止不良数据。至少，您应该为压缩数据计算校验和。如果您需要免受黑客保护，请使用LZ4_decompress_safe函数。其他选择：采用加密哈希函数作为校验和（尽管这可能会破坏性能）；为缓冲区分配更多的内存；通过单独的mmap调用为缓冲区分配内存并创建保护页。

当我看到复制8字节数据的代码时，我立即想知道为什么正好是8字节。您可以使用SSE寄存器复制16个字节：

 inline void copy16(UInt8 * dst, const UInt8 * src) { #if __SSE2__    _mm_storeu_si128(reinterpret_cast<__m128i *>(dst),        _mm_loadu_si128(reinterpret_cast<const __m128i *>(src))); #else    memcpy(dst, src, 16); #endif } inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end) {    do    {        copy16(dst, src);        dst += 16;        src += 16;    } while (dst < dst_end); }

复制AVX的32字节和AVX-512的64字节时，同样的工作。此外，您可以多次展开循环。如果您曾经看过memcpy的实现方式，那么这就是所使用的方法。（顺便说一句，在这种情况下，编译器将不会展开或向量化循环，因为这将需要插入大量检查。）

为什么原始的LZ4实现不这样做？首先，尚不清楚这是好是坏。所获得的增益取决于要复制的块的大小，因此，如果它们都较短，那么它将无所作为而产生额外的工作。其次，它破坏了LZ4格式的规定，这些规定有助于避免内部循环中不必要的分支。

但是，我们暂时会记住此选项。

棘手的复制

让我们回到是否总是有可能以这种方式复制数据的问题。假设我们需要复制一个匹配项，即从位于游标后面某个偏移处的输出缓冲区中获取一块内存，然后将其复制到游标位置。

想象一个简单的情况，当您需要以偏移量12复制5个字节时：

Hello world ...........
^^^^^ - src
^^^^^ - dst

Hello world Hello wo ...
^^^^^ - src
^^^^^ - dst

但是，当我们需要复制一个比偏移量更长的内存块时，情况更加困难。换句话说，它包含一些尚未写入输出缓冲区的数据。

复制10个字节，偏移量为3：

abc .............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

abc abcabcabca ...
^^^^^^^^^^ - src
^^^^^^^^^^ - dst

我们在压缩过程中拥有所有数据，很可能会找到这样的匹配项。 memcpy函数不适用于复制它，因为它不支持存储块范围重叠的情况。 memmove函数也不起作用，因为尚未完全初始化应从中获取数据的内存块。我们需要采用与逐字节复制相同的方式进行复制。

 op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ...

运作方式如下：

a bc a ............
^ - src
^ - dst

a b ca b ...........
^ - src
^ - dst

ab c ab c ..........
^ - src
^ - dst

abc a bc a .........
^ - src
^ - dst

abca b ca b ........
^ - src
^ - dst

换句话说，我们必须创建一个重复序列。 LZ4的原始实现使用一些令人惊讶的奇怪代码来执行此操作：

 const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4}; const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3}; const int dec64 = dec64table[offset]; op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; match += dec32table[offset]; memcpy(op+4, match, 4); match -= dec64;

它一个接一个地复制前4个字节，向前跳过一个幻数，完全复制接下来的4个字节，然后使用另一个幻数将光标移至匹配项。代码的作者（ Yan Collet ）以某种方式忘记了对这意味着什么的评论。此外，变量名称令人困惑。它们都被命名为dec ... table，但是一个被添加，另一个被减去。此外，其中一个是无符号的，另一个是int的。但是，作者最近在代码中改进了该位置。

实际上是这样的。我们一次复制前四个字节：

abc abca .........
^^^^ - src
^^^^ - dst

现在我们可以一次复制4个字节：

abcabca bcab .....
^^^^ - src
^^^^ - dst

我们可以照常继续，一次复制8个字节：

abcabcabcab cabcabca .....
^^^^^^^^ - src
^^^^^^^^ - dst

众所周知，有时理解代码的最佳方法是重写代码。这是我们想到的：

 inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    /// Or if 4 % n is zero, we use n.    /// It gives an equivalent result, but is more CPU friendly for unknown reasons.    static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset]; }

不出所料，这根本不会改变性能。我只是真的想尝试一次复制16个字节的优化。

但是，这使“特殊情况”复杂化，并导致更频繁地调用它（ offset < 16条件至少与offset < 8一样频繁地执行）。使用16字节复制来复制重叠范围如下所示（仅显示开头）：

 inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset) {    /// 4 % n.    static constexpr int shift1[]        = { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 };    /// 8 % n - 4 % n    static constexpr int shift2[]        = { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 };    /// 16 % n - 8 % n    static constexpr int shift3[]        = { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 };    op[0] = match[0];    op[1] = match[1];    op[2] = match[2];    op[3] = match[3];    match += shift1[offset];    memcpy(op + 4, match, 4);    match += shift2[offset];    memcpy(op + 8, match, 8);    match += shift3[offset]; }

可以更有效地执行此功能吗？我们想找到一种神奇的SIMD指令来处理这种复杂的代码，因为我们要做的就是写入16个字节，该字节完全由几个字节的输入数据组成（从1到15）。然后，只需按照正确的顺序重复它们。

像这样的一条指令称为pshufb （打包的洗牌字节），它是SSSE3（三个S）的一部分。它接受两个16字节寄存器。寄存器之一包含源数据。另一个具有“选择器”：每个字节包含一个从0到15的数字，具体取决于要从中获取结果的源寄存器的哪个字节。如果选择器的字节值大于127，则结果的相应字节将填充为零。

这是一个例子：

  xmm0：abc .............
 xmm1：0120120120120120

 pshufb％xmm1，％xmm0

 xmm0：abcabcabcabcabca

结果的每个字节都填充有源数据的选定字节-这正是我们所需要的！结果中的代码如下所示：

 inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset) { #ifdef __SSSE3__    static constexpr UInt8 __attribute__((__aligned__(16))) masks[] =    {        0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */        0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,        0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0,        0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,        0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0,        0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7,        0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1,        0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0,    };    _mm_storeu_si128(reinterpret_cast<__m128i *>(op),        _mm_shuffle_epi8(            _mm_loadu_si128(reinterpret_cast<const __m128i *>(match)),            _mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset)));    match += masks[offset]; #else    copyOverlap16(op, match, offset); #endif }

_mm_shuffle_epi8是一个内在函数，可编译为pshufb CPU指令。

我们可以使用更新的指令一次执行更多字节的操作吗？毕竟，SSSE3是一个非常古老的指令集，自2006年以来就存在。AVX2的指令一次可对32个字节执行此操作，但可对单个16字节通道进行此操作。这被称为向量置换字节，而不是打包的洗牌字节-字是不同的，但是含义是相同的。 AVX-512 VBMI还有另一条指令可同时处理64个字节，但是支持该指令的处理器只是最近才出现。 ARM NEON具有类似的指令，称为vtbl（向量表查找），但它们仅允许写入8个字节。

此外，还有一个带有64位MMX寄存器的pshufb指令版本，以便形成8个字节。替换代码的原始版本是正确的。但是，我决定改用16字节选项（出于严重原因）。

在Highload ++ Siberia会议上，一位与会者在我演讲后向我走来，并提到对于8字节的情况，您可以使用乘以一个特殊选择的常量（您还需要一个偏移量）-甚至都没有发生以前对我！

如何删除多余的if语句

假设我要使用一个复制16个字节的变体。如何避免必须对缓冲区溢出进行额外检查？

我决定不做这项检查。该函数的注释将表明，开发人员应为超出指定数量的指定字节数分配一块内存，以便我们可以在那里读写不必要的垃圾。函数的接口将更难使用，但这是一个不同的问题。

实际上，可能会有负面后果。假设我们需要解压缩的数据是由65,536字节的块组成的。然后，用户为我们提供了一个65,536字节的内存，用于解压缩的数据。但是使用新功能接口时，将要求用户分配一个65,551字节的存储块。然后，根据其实现，分配器可能被迫实际分配96甚至128 KB。如果分配器非常糟糕，它可能会突然停止在“堆”中缓存内存，并每次都使用mmap和munmap进行内存分配（或使用madvice释放内存）。由于页面错误，此过程将非常缓慢。结果，这点优化可能最终会减慢一切。

有加速吗？

因此，我制作了使用三个优化的代码版本：

复制16个字节而不是8个字节。
对于offset < 16情况，请使用随机播放指令。
如果删除了一个额外的。

我开始在不同的数据集上测试此代码，并获得了意外的结果。

范例1：
Xeon E2650v2，Yandex浏览器数据，AppVersion列。
参考：1.67 GB /秒。
16字节，随机播放：2.94 GB /秒（速度提高76％）。

范例2：
Xeon E2650v2，Yandex Direct数据，ShowsSumPosition列。
参考：2.30 GB /秒。
16字节，随机播放：1.91 GB /秒（慢20％）。

起初我真的很高兴，当我看到一切都以如此大的速度加速了。然后，我发现其他文件的运行速度没有任何提高。对于某些人来说，速度甚至要慢一些。我得出的结论是，结果取决于压缩率。文件压缩得越多，切换到16个字节的优势就越大。感觉很自然：压缩率越大，要复制的片段的平均长度越长。

为了进行调查，我使用C ++模板为四种情况提供了代码选项：使用8字节或16字节的块，以及带有或不带有shuffle指令。

 template <size_t copy_amount, bool use_shuffle> void NO_INLINE decompressImpl(    const char * const source,    char * const dest,    size_t dest_size)

完全不同的代码变体在不同文件上的表现更好，但是在台式机上进行测试时，总是会获得带有随机播放功能的版本。在桌面上进行测试很不方便，因为您必须这样做：

 sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium)

然后，我使用一台旧的“开发”服务器（使用Xeon E5645处理器），获取了更多数据集，并得到了几乎相反的结果，这完全使我感到困惑。事实证明，除了压缩率以外，最佳算法的选择还取决于处理器模型。处理器确定何时最好使用随机播放指令，以及何时开始使用16字节复制的阈值。

顺便说一句，在我们的服务器上进行测试时，这样做很有意义：

 sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client)

否则，结果将不稳定。还要注意热节流和功率上限。

如何选择最佳算法

因此，我们有四种算法变体，我们需要为条件选择最佳的一种。我们可以创建一组具有代表性的数据和硬件，然后执行严格的负载测试并选择平均水平最佳的方法。但是我们没有代表性的数据集。为了进行测试，我使用了Yandex Metrica ，Yandex Direct，Yandex Browser和美国航班的数据样本。但是，这还不够，因为ClickHouse被全球数百家公司使用。通过对一个数据集进行过度优化，我们可能会导致其他数据的性能下降甚至没有意识到。如果结果取决于处理器模型，我们将必须在代码中明确编写条件并在每个模型上对其进行测试（或参考时序说明参考手册，您认为呢？）。无论哪种情况，这都非常耗时。

因此，我决定使用另一种方法，这对在我们的数据分析学院学习的同事来说是显而易见的： “多臂匪徒” 。关键是算法的变体是随机选择的，然后我们使用统计数据逐渐选择性能更好的选项。

我们有许多数据块需要解压缩，因此我们需要独立的函数调用来解压缩数据。我们可以为每个块选择四种算法之一，并测量其执行时间。与处理数据块相比，这样的操作通常不花费任何费用，并且在ClickHouse中，未压缩的数据块至少为64 KB。（阅读有关测量时间的文章。）

为了更好地理解“多臂匪”算法的工作原理，让我们看一下名称的来源。这类似于赌场中的老虎机，玩家可以拉几个杠杆以获取一些随机的钱。玩家可以按任意顺序多次拉动操纵杆。每个杠杆都有一定的概率发出相应的钱，但是玩家不知道其运作方式，只能从玩游戏的经验中学习。一旦弄清楚了，他们就可以最大限度地赢得奖金。

最大化奖励的一种方法是，根据先前步骤中的游戏统计信息，评估每个步骤中每个杠杆的概率分布。然后，我们根据收到的分配在精神上为每个杠杆“赢得”随机奖励。最终，我们拉动了在心理游戏中取得最佳结果的杠杆。这种方法称为汤普森采样。

但是我们正在选择一种解压缩算法。结果是执行时间（以每字节皮秒为单位）：越少越好。我们将执行时间视为一个随机变量，并使用数学统计数据评估其分布。贝叶斯方法通常用于这样的任务，但是将复杂的公式插入C ++代码会很麻烦。我们可以使用参数方法，说一个随机变量属于随机变量的参数族，然后评估其参数。

我们如何选择随机变量族？例如，我们可以假设代码执行时间具有正态分布。但这是绝对错误的。首先，执行时间不能为负，正态分布在数字行的任何地方都取值。其次，我假设执行时间在正确的一端会有一个沉重的“尾巴”。

但是，有一些因素可能使仅出于汤普森抽样的目的估计正态分布成为一个好主意（尽管目标变量的分布不一定是正态的事实）。原因是计算数学期望和方差非常容易，并且经过足够的迭代次数后，正态分布变得相当狭窄，与我们使用其他方法获得的分布差别不大。如果我们不太关心第一步的收敛速度，则可以忽略这些细节。

This may seem like a somewhat ignorant approach. Experience has shown us that the average time for query execution, website page loading, and so on is "garbage" that isn't worth calculating. It would be better to calculate the median, which is a robust statistic . But this is a little more difficult, and as I will show later, the described method justifies itself for practical purposes.

At first I implemented calculation of the mathematical expectation and variance, but then I decided that this is too good, and I need to simplify the code to make it "worse":

 /// For better convergence, we don't use proper estimate of stddev. /// We want to eventually separate the two algorithms even in cases /// when there is no statistical significant difference between them. double sigma() const {    return mean() / sqrt(adjustedCount()); } double sample(pcg64 & rng) const {    ...    return std::normal_distribution<>(mean(), sigma())(rng); }

I wrote it so that the first few iterations were not taken into account, to eliminate the effect of memory latencies.

The result is a test program that can select the best algorithm for the input data, with optional modes that use the reference implementation of LZ4 or a specific version of the algorithm.

So there are six options:
— Reference (baseline): original LZ4 without our modifications.
— Variant 0: copy 8 bytes at a time without shuffle.
— Variant 1: copy 8 bytes at a time with shuffle.
— Variant 2: copy 16 bytes at a time without shuffle.
— Variant 3: copy 16 bytes at a time with shuffle.
— The "bandit" option, which selects the best of the four optimized variants.

Testing on different CPUs

If the result strongly depends on the CPU model, it would be interesting to find out exactly how it is affected. There might be an exceptionally large difference on certain CPUs.

I prepared a set of datasets from different tables in ClickHouse with real data, for a total of 256 different files each with 100 MB of uncompressed data (the number 256 was coincidental). Then I looked at the CPUs of the servers where I can run benchmarks. I found servers with the following CPUs:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz

The most interesting part comes next — the processors provided by the R&D department:
— AMD EPYC 7351 16-Core Processor, a new AMD server processor.
— Cavium ThunderX2, which is AArch64, not x86. For these, my SIMD optimization needed to be reworked a bit. The server has 224 logical and 56 physical cores.

There are 13 servers in total, and each of them runs the test on 256 files in 6 variants (reference, 0, 1, 2, 3, adaptive). The test is run 10 times, alternating between the options in random order. It outputs 199,680 results that we can compare.

For example, we can compare different CPUs with each other. But we shouldn't jump to conclusions from these results, because we are only testing the LZ4 decompression algorithm on a single core (this is a very narrow case, so we only get a micro-benchmark). For example, the Cavium has the lowest performance per single core. But I tested ClickHouse on it myself, and it wins out over Xeon E5-2650 v2 on heavy queries due to the greater number of cores, even though it is missing many optimizations that are made in ClickHouse specifically for the x86.

 ┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐
│ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │
│ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │
│ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │
│ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │
│ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │
│ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │
│ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │
│ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │
│ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │
│ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │
│ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │
└───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘

ref, adapt, max — The speed in gigabytes per second (the value that is the reverse of the arithmetic mean of time for all launches on all datasets).
best — The number of the best algorithm among the optimized variants, from 0 to 3.
adapt_boost — The relative advantage of the adaptive algorithm compared to the baseline.
max_boost — The relative advantage of the best of the non-adaptive variants compared to the baseline.
adapt_over_max — The relative advantage of the adaptive algorithm over the best non-adaptive one.

The results show that we were able to speed up decompression by 12-20% on modern x86 processors. Even on ARM we saw 4% improvement, despite the fact that we didn't optimize much for this architecture. It is also clear that on average for different datasets, the "bandit" algorithm comes out ahead of the pre-selected best variant on all processors (except for very old Intel CPUs).

结论

In practice, the usefulness of this work is dubious. Yes, LZ4 decompression was accelerated on average by 12-20%, and on some datasets the performance more than doubled. But in general, this doesn't have much effect on query execution time. It's difficult to find real queries that gain more than a couple percent in speed.

We decided to use ZStandard level 1 instead of LZ4 on several Yandex Metrica clusters intended for executing long queries, because it is more important to save IO and disk space on cold data. Keep this in mind if you have similar workload.

We observed the greatest benefits from optimizing decompression in highly compressible data, such as columns with mostly duplicate string values. However, we have developed a separate solution specifically for this scenario that allows us to significantly speed up queries over this kind of data.

Another point to remember is that optimization of decompression speed is often limited by the format of the compressed data. LZ4 uses a very good format, but Lizard, Density and LZSSE have other formats that can work faster. Perhaps instead of trying to accelerate LZ4, it would be better to just integrate LZSSE into ClickHouse.

It's unlikely that these optimizations will be implemented in the mainstream LZ4 library: in order to use them, the library interface would have to be modified. In fact, this is often the case with improving algorithms — optimizations don't fit into old abstractions and they have to be revised. However, variable names have already been corrected in the original implementation. For instance, inc and dec tables have been corrected . In addition, about a month ago, the original implementation accelerated decompression by the same 12-15% by copying 32 bytes instead of 16, as discussed above. We tried the 32-byte option ourselves and the results were not that great, but they were still faster .

If you look at the profile at the beginning of the article, you may notice that we could have removed one extra copying operation from the page cache to userspace (either using mmap , or using O_DIRECT and userspace page cache, but both options are problematic). We also could have slightly improved the checksum calculation (CityHash128 is currently used without CRC32-C, but we could use HighwayHash, FARSH or XXH3). Acceleration of these two operations is useful for weakly compressed data, since they are performed on compressed data.

In any case, the changes have already been added to master more than a year ago, and the ideas that resulted from this research have been applied in other tasks. You can also watch the video from HighLoad++ Siberia, or view the presentation (both in Russian).

如何在ClickHouse中加快LZ4解压缩？