协整关系的对称性

本文的目的是在时间序列的协整研究中分享矛盾的结果：如果时间序列 $$与附近共同整合 $$$B$ 排 $$$B$ 并非总是与数字共同集成 $$。

如果我们纯粹从理论上研究协整，那么很容易证明 $$与...共同整合 $$$B$ 然后排 $$$B$ 与...共同整合 $$。 但是，如果我们开始凭经验研究协整，事实证明理论计算并不总是得到证实。 为什么会这样呢？

对称性

态度 $$如果称为对称 $$$A \ subseteq A ^ {-1}$ 在哪里 $$$A ^ {-1}$ -条件定义的反比： $$$x A ^ {-1} y$ 等于 $$$yAx$ 。 换句话说，如果关系 $$$xAy$ 然后关系 $$$yAx$ 。

考虑两个 $$$我（1）$ 一些 $$$x_t$ 和 $$$y_t$ ， $$$t = 0，\点，T$ 。 协整是对称的，如果 $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ 需要 $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ 也就是说，如果直接回归的存在导致逆的存在。

考虑方程式 $$$y_t = \ beta_1 x_t + \ varepsilon_ {1t}$ ， $$$\ beta_1 \ neq 0$ 。 左右互换并减去 $$$\ varepsilon_ {1t}$ 从两个部分： $$$\ beta_1 x_t = y_t-\ varepsilon_ {1t}$ 。 由于 $$$\ beta_1 \ neq 0$ 根据定义，将这两个部分分为 $$$\ beta_1$ ：

$$

$$x_t = \ frac {1} {\ beta_1} y_t-\ frac {\ varepsilon_ {1t}} {\ beta_1}$$

更换 $$$1 / \ beta_1$ 在 $$$\ beta_2$ 和 $$$-\ varepsilon_ {1t} / \ beta_1$ 在 $$$\ varepsilon_ {2t}$ 我们得到 $$$x_t = \ beta_2 y_t + \ varepsilon_ {2t}$ 。 因此，协整关系是对称的。

因此，如果变量 $$$X$ 与变量协整 $$$Y$ 然后变量 $$$Y$ 必须与变量共同集成 $$$X$ 。 但是，角度-格兰杰协整检验并不总能证实这种对称性，因为有时 $$$Y$ 不与变量协整 $$$X$ 根据这个测试。

我使用Angle-Granger检验在2017年莫斯科和纽约交易所的数据上测试了对称性。 莫斯科证券交易所共有7,975对股份。 对于7731（97％）共整合对，确认了对称性，对于244（3％）共整合对，未确认对称性。

纽约证券交易所共有140,903对联合整合的股票。 对于136586（97％）个协整对，确认了对称性，对于4317（3％）协整对，未确认对称性。

口译

第二种Dickey-Fuller检验是基于角度-格兰杰（Angle-Granger）检验的，它的低功效和高错误概率可以解释这一结果。 第二种错误的概率可以表示为 $$$\ beta = P（H_0 | H_1）$ 然后值 $$$1-\ beta$ 称为测试的力量。 不幸的是，Dickey-Fuller测试无法区分非平稳时间序列和非平稳时间序列。

什么是近乎不稳定的时间序列？ 考虑时间序列 $$$x_t = \ phi x_ {t-1} + \ varepsilon_t$ 。 固定时间序列是其中 $$$0 <\ phi <1$ 。 非平稳时间序列是其中 $$$\ phi = 1$ 。 近似不稳定的时间序列是其中值 $$$\ phi$ 接近一个。

在接近非平稳时间序列的情况下，我们通常无法拒绝非平稳时间的原假设。 这意味着Dickey-Fuller检验具有第二种错误的高风险，即不拒绝错误的原假设的可能性。

KPSS测试

对Dickey-Fuller检验的弱点的一种可能的应对方法是KPSS检验，其名称得益于Kvyatkovsky，Phillips，Schmidt和Sheen的科学家的名字缩写。 尽管此检验的方法论方法与Dickey-Fuller方法完全不同，但主要的区别应理解为零假设和替代假设的排列。

在KPSS检验中，零假设指出时间序列是平稳的，而不是关于存在非平稳性的选择。 使用Dickey-Fuller检验通常被确定为非平稳的近非平稳时间序列，可以使用KPSS检验正确地确定为非平稳的时间序列。

但是，我们必须意识到，统计检验的任何结果都只是概率性的，不应与某个真实的判断相混淆。 我们总是有一个非零的错误概率。 因此，建议将Dickey-Fuller和KPSS测试的结果结合起来，作为非平稳性的理想测试。



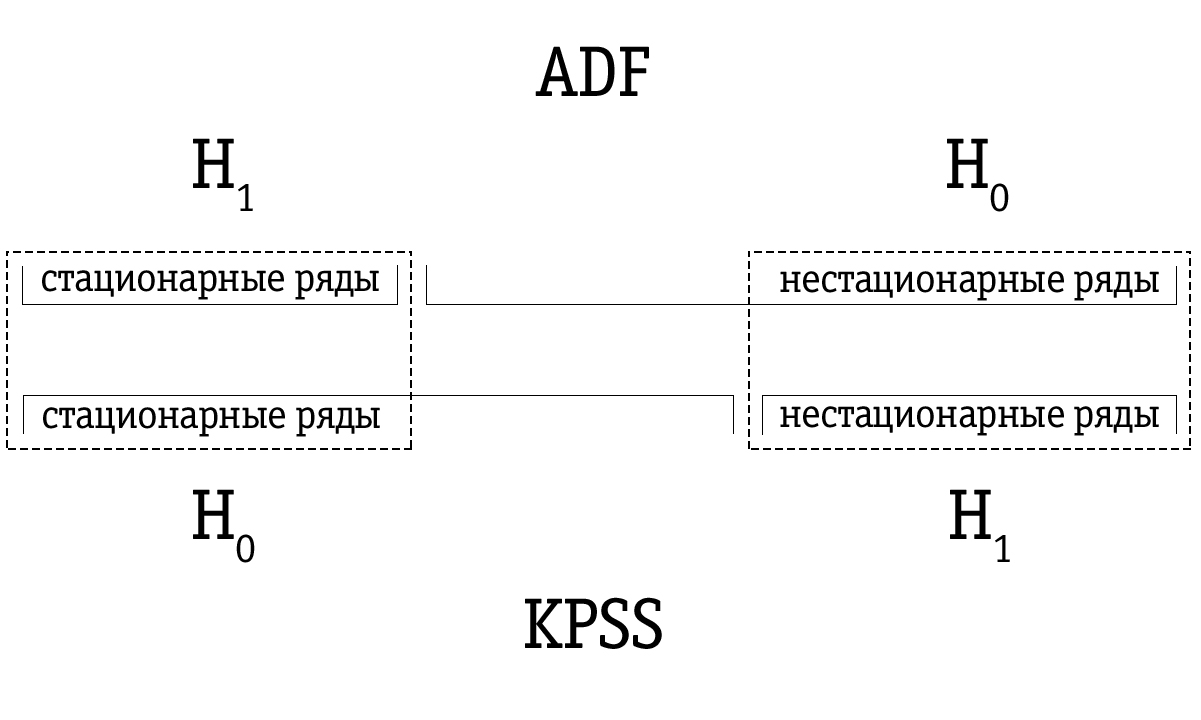
由于功率较低，Dickey-Fuller测试经常错误地将一个序列确定为非平稳的，因此与许多使用KPSS测试确定为非平稳的时间序列相比，Dickey-Fuller测试确定为不稳定的时间序列集更大。 因此，测试顺序很重要。

如果使用Dickey-Fuller检验将时间序列确定为固定时间，则很可能也将使用KPSS检验将时间序列确定为固定时间； 在这种情况下，我们可以假设该序列确实是固定的。

如果使用KPSS检验将时间序列确定为不稳定，那么使用Dickey-Fuller检验也很可能将其确定为不稳定。 在这种情况下，我们可以假设序列确实不稳定。

但是，经常发生的情况是，使用Dickey-Fuller检验被确定为非平稳的时间序列将通过KPSS检验被标记为平稳。 在这种情况下，我们必须非常谨慎地对待最终结论。 我们可以检查在KPSS检验中平稳性的基础是否牢固，在Dickey-Fuller检验中平稳性的基础是否牢固，并做出适当的决定。 当然，我们也可以不解决这种时间序列的平稳性问题。

KPSS测试方法假设时间序列 $$$y_t$ 相对于趋势进行平稳性检验的结果可以分解为确定性趋势的总和 $$$\ beta t$ 随机游走 $$$r_t$ 和固定误差 $$$\ varepsilon_t$ ：

$$

$$y_t = \ beta t + r_t + \ varepsilon_t，\\ r_t = r_ {t-1} + u_t，$$

在哪里 $$$u_t$ -均值和方差为零的正常iid过程 $$$\ sigma ^ 2$ （ $$$u_t \ sim N（0，\ sigma ^ 2）$ ） 初始值 $$$r_0$ 被视为固定成员，并扮演自由成员的角色。 固定误差 $$$\ varepsilon_t$ 可以由任何常见的ARMA流程生成，也就是说，它可以具有很强的自相关。

与Dickey-Fuller检验相似，考虑自相关的任意结构的能力 $$$\ varepsilon_t$ 非常重要，因为大多数经济时间序列都高度依赖时间，因此具有很强的自相关性。 如果要检查相对于水平轴的平稳性，则该术语 $$$\ beta t$ 只是从上面的等式中排除。

从上面的方程式可以得出原假设 $$$H_0$ 关于平稳 $$$y_t$ 等同于假设 $$$\ sigma ^ 2 = 0$ ，由此得出 $$$r_t = r_0$ 对于所有 $$$t$ （ $$$r_0$ 是一个常数）。 同样，另一种假设 $$$H_1$ 非平稳性等于假设 $$$\ sigma ^ 2 \ neq 0$ 。

检验假设 $$$H_0$ ： $$$\ sigma ^ 2 = 0$ （固定时间序列）与替代 $$$H_1$ ： $$$\ sigma ^ 2 \ neq 0$ （非平稳时间序列）KPSS测试的作者收到拉格朗日乘数测试的单向统计信息。 他们还计算其渐近分布并为渐近临界值建模。 在这里我们不考虑理论上的细节，而只是简要概述测试执行算法。

对时间序列执行KPSS测试时 $$$y_t$ ， $$$t = 1，\点，T$ 最小二乘法（最小二乘）用于估计以下方程式之一：

$$

$$y_t = a_0 + \ varepsilon_t，\\ y_t = a_0 + \ beta t + \ varepsilon_t$$

如果要检查相对于水平轴的平稳性，我们可以评估第一个方程。 如果我们计划检查趋势的平稳性，则选择第二个方程。

剩菜剩饭 $$$e_t$ 根据估计方程式计算拉格朗日乘数检验的统计量。 拉格朗日乘数检验基于以下思想：当满足零假设时，所有拉格朗日乘数必须等于零。

拉格朗日乘数检验

拉格朗日乘数检验与使用最大似然法（ML）的更通用的参数估计方法相关联。 根据这种方法，数据被认为是与分布参数有关的证据。 证据表示为未知参数的函数-似然函数：

$$

$$L（X_1，X_2，X_3，\点，X_n; \ Phi_1，\ Phi_2，\点，\ Phi_k），$$

在哪里 $$$X_i$ 是观测值，并且 $$$\披_$ -我们要评估的参数。

最大似然函数是样本观察的联合概率。

$$

$$L（X_1，X_2，X_3，\点，X_n; \ Phi_1，\ Phi_2，\点，\ Phi_k）= P（X_1 \地X_2 \地X_3 \点X_n）$$

最大似然法的目的是使似然函数最大化。 这是通过微分每个估计参数的最大概率函数并将偏导数等于零来实现的。 函数值最大的参数值是所需的估计值。

通常，为了简化后续工作，首先采用似然函数的对数。

考虑广义线性模型 $$$Y = \ beta X + \ varepsilon$ 假设 $$$\ varepsilon$ 正态分布 $$$N（0，\ sigma ^ 2）$ 那就是 $$$Y-\ beta X \ sim N（0，\ sigma ^ 2）$ 。

我们要检验系统的假设 $$$q$ （ $$$q <k$ ）独立的线性约束 $$$R \ beta = r$ 。 在这里 $$$R$ -著名 $$$q \乘以k$ 秩矩阵 $$$q$ 和 $$-著名 $$$q \乘以1$ 向量。

对于每对观测值 $$$X$ 和 $$$Y$ 在正常情况下，将存在以下形式的概率密度函数：

$$

$$f（X_i，Y_i）= \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {-\ frac {1} {2} \ left（\ frac {Y_i-\ beta X_i} {\ sigma} \ right）^ 2}$$

受制于 $$$n$ 联合观察 $$$X$ 和 $$$Y$ 观察样本中所有值的总概率等于概率密度函数各个值的乘积。 因此，似然函数定义如下：

$$

$$L（\ beta）= \产品\极限_ {i = 1} ^ n \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {-\ frac {1} {2} \ left （\ frac {Y_i-\ beta X_i} {\ sigma} \ right）^ 2}$$

由于求和比求积容易，因此通常采用似然函数的对数，因此：

$$

$$\ ln L（\ beta）= \ sum \ limits_ {i = 1} ^ n \ left（\ ln \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}}-\ frac {1} { 2 \ sigma ^ 2}（Y_i-\ beta X_i）^ 2 \ right）$$

这种有用的转换不会影响最终结果，因为 $$$\ ln L$ 是增加功能 $$$L$ 。 那么那么价值 $$$\ beta$ 最大化 $$$\ ln L$ 也将最大化 $$$L$ 。

的ML分数 $$$\ beta$ 有限制地回归 $$$R \ beta = r$ ）是通过使函数最大化而获得的 $$$\ ln L（\ beta）$ 服从 $$$R \ beta = r$ 。 为了找到这个估计，我们编写了Lagrange函数：

$$

$$\ psi（\ beta）= \ ln L（\ beta）-g'（R \ beta-r），$$

通过哪里 $$$g = \左（g_1，\点，g_q \右）'$ 标记的矢量 $$$q$ 拉格朗日乘数。

拉格朗日乘数检验统计量表示为 $$$\ eta_ \亩$ 如果相对于水平轴平稳且通过 $$$\ eta_ \ tau$ 在相对于趋势平稳的情况下，由以下表达式确定

$$

$$\ eta _ {\ mu / \ tau} = T ^ 2 \ frac {1} {s ^ 2（l）} \ sum \ limits_ {t = 1} ^ T S_t ^ 2，$$

在哪里

$$

$$S_t = \ sum \ limits_ {i = 1} ^ t e_i$$

和

$$

$$s ^ 2（l）= T ^ {-1} \ sum \ limits_ {t = 1} ^ T e_t ^ 2 + 2 T ^ {-1} \ sum \ limits {{1} ^ lw（s，l） \ sum \ limits_ {t = s + 1} ^ T e_t e_ {ts}，$$

在哪里

$$

$$w（s，l）= 1-\ frac {s} {l + 1}$$

在以上等式中 $$$S_t$ -部分余额的过程 $$$e_t$ 根据估计方程 $$$s ^ 2（l）$ -评估残留物的长期分散 $$$e_t$ ; 但是 $$$w（s，l）$ -所谓的巴特利特光谱窗口，其中 $$$l$ -滞后截断参数。

在此应用中，光谱窗口用于估计在一定间隔（窗口）内的误差的光谱密度，该间隔沿系列的整个范围移动。 间隔之外的数据将被忽略，因为窗口函数是某个选定间隔（窗口）之外等于零的函数。

方差估计 $$$s ^ 2（l）$ 取决于参数 $$$l$ ，以及 $$$l$ 增加且大于0，得分 $$$s ^ 2（l）$ 开始考虑残差可能的自相关 $$$e_t$ 。

最后，拉格朗日乘数检验统计 $$$\ eta_ \亩$ 或 $$$\ eta_ \ tau$ 与临界值比较。 如果拉格朗日乘数检验的统计量超过了相应的临界值，则原假设 $$$H_0$ （固定时间序列）偏向替代假设 $$$H_1$ （非平稳时间序列）。 否则，我们不能拒绝原假设 $$$H_0$ 关于时间序列的平稳性。

临界值是渐近的，因此最适合大样本量。 但是，实际上它们也用于少量样品。 此外，临界值与参数无关 $$$l$ 。 但是，拉格朗日乘数检验的统计信息将取决于参数 $$$l$ 。 KPSS测试的作者没有提供任何用于选择适当参数的通用算法。 $$$l$ 。 该测试通常针对 $$$l$ 在0到8的范围内。

随着增加 $$$l$ 我们不太可能拒绝原假设 $$$H_0$ 关于平稳性，这部分导致测试功效的降低，并且可能给出不同的结果。 但是，总的来说，我们可以说如果原假设 $$$H_0$ 时间序列的平稳性即使在很小的值下也不会被拒绝 $$$l$ （0、1或2），我们得出结论，验证的时间序列是固定的。

测试结果比较

开发了以下方法来评估对称的可能性。

1. 使用Dickey-Fuller检验以0.05的显着性水平检查所有时间序列的一阶可积性。 下面仅考虑一阶可积级数。
2. 在第1节中获得的一阶可积级数通过不重复地组合而组成对。
3. 使用Angle-Granger检验对第2节中得出的成对股票进行协整检验。 结果，识别出协整对。
4. 使用KPSS检验对通过第3款中的检验结果获得的回归残基进行平稳性检验。 因此，将两个测试的结果合并。
5. 将交换第2节中协整对中的时间序列，并使用Angle-Granger检验再次检查协整，即，我们检查时间序列之间的关系是否对称。
6. 互换项目4的协整对中的时间序列，并使用KPSS检验再次检查回归残差的平稳性，即，我们将检查时间序列之间的关系是否对称。

所有计算均使用MATLAB软件包执行。 结果列在下表中。 对于每个测试，我们都有许多根据测试结果对称的关系（标记为 $$$S$ ）; 根据测试结果，我们有许多不对称的关系（标记为 $$$¬$ ）; 并且根据测试结果，该比率具有对称性的经验概率（ $$$P（S）= \ frac {S} {S +¬S}$ ）

在莫斯科交易所：


在纽约证券交易所：

回测结果比较

让我们比较一下使用Angle-Granger检验选择的协整对和使用KPSS检验选择的协整对的历史数据的交易策略结果。

从表中可以看出，由于可以更准确地识别共同集成的股票对，因此交易单独的共同集成的股票对可以使平均年收益率提高9.21％。 因此，所提出的方法可以使用市场中立策略来提高算法交易的获利能力。

替代解释

正如我们在上面看到的，Angle-Granger测试的结果是彩票。 在某些情况下，我的想法似乎过于笼统，但我认为，不要对信念采用统计分析所证实的零假设是很有意义的。

检验假设的科学方法的保守性在于，在分析数据时，我们只能得出一个有效的结论：原假设在所选的显着性水平上被拒绝。 这并不意味着替代方案是正确的。 $$$H_1$ -我们只是根据典型的“相反证据”获得了其可信度的间接证据。 在真实的情况下 $$$H_0$ ，还要求研究人员做出谨慎的结论：根据在实验条件下获得的数据，不可能找到足够的证据来拒绝原假设。

与我在2018年9月的想法一致，有影响力的人们写了一篇文章 ，呼吁放弃“统计意义”的概念以及检验原假设的范式。

最重要的是：“诸如更改阈值级别的建议 $$$p$ -默认值，使用置信区间（重点在于它们是否包含零）或使用贝叶斯系数以及普遍接受的分类来评估来自与当前使用相同或相似的所有问题的证据的强度 $$$p$ 值为0.05 ...的值是一种统计炼金术，它错误地承诺将随机性转变为可靠性，即所谓的“不确定性洗钱”（Gelman，2016年），其始于数据，最后以关于真相或虚假的二分式结论结束-二元陈述“有效果”或“无效果”-是在实现某些目标的基础上 $$$p$ 值或其他阈值。

(Carlin, 2016; Gelman, 2016), , ( ) , , .»

结论

我们看到，尽管从理论上应满足协整关系的对称性，但实验数据与理论计算有所不同。 这种悖论的一种解释是Dickey-Fuller测试的低功耗。

作为一种识别共集成资产对的新方法，提出了使用KPSS检验来测试使用Angle-Granger检验获得的回归残差的平稳性，并结合这些检验的结果； 并结合Angle-Granger检验和KPSS检验的结果进行正向和反向回归。

对莫斯科交易所2017年的数据进行了回测。 根据回溯测试的结果，使用上述提议的识别组合股对的方法时的平均年收益率为22.72％。 因此，与使用Angle-Granger检验识别共同整合的股票对相比，可以将平均年收益提高9.21％。

悖论的另一种解释是不采用经统计分析证实的对信念的零假设。 原假设检验范式和这种范式提供的二分法给我们一种错误的市场知识感。

当我刚开始研究时，在我看来，您可以占领市场，将其放入统计测试的“绞肉机”中，并在出口处过滤掉美味的行。 不幸的是，现在我看到统计暴力的概念将行不通。

市场上是否存在协整—对我来说，这个问题仍然悬而未决。 对于该理论的创始人，我仍然有很大的疑问。 我曾经在西方和那些在计量经济学被视为苏联的腐败资产阶级的时候发展金融数学的科学家感到不安。 在我看来，我们已经远远落后了，在欧洲和美国的某个地方，金融之神坐在那里，他们知道真理的圣杯。

现在，我了解到，欧美科学家与我们的科学家并没有太大区别，唯一的区别是夸克的规模。 我们的科学家坐在一座象牙城堡里，他们写些废话，并获得50万卢布的赠款。 在西方，大约同一位科学家坐在同一座象牙城堡里，他们写着同样的废话，并为此获得“诺贝尔奖”和50万美元的赠款。 就是全部了。

目前，我对我的研究主题尚无明确的看法。 说“所有对冲基金都使用成对交易”是错误的，因为大多数对冲基金也都破产了。

不幸的是，您总是必须用自己的头脑去思考和决策，尤其是在我们冒钱的时候。