哈Ha! 我向您介绍了Akarsh Zingade撰写的文章
“使用深度排名的图像相似性”的翻译。
深度排名算法
没有介绍“
两个图像的相似性 ”的概念,因此让我们至少在本文的框架内介绍这个概念。
两个图像的相似性是根据某些标准比较两个图像的结果。 它的定量度量确定了两个图像的强度图之间的相似程度。 使用相似性度量,比较描述图像的某些特征。 汉明距离,欧几里得距离,曼哈顿距离等是相似度的度量。
深度排名 -研究细粒度的图像相似度,使用一组三元组表征精细划分的图像相似度比率。
什么是三胞胎?
三元组包含请求图像,正图像和负图像。 正图像比负图像更像是请求图像。
一组三元组的示例:
第一,第二和第三行对应于请求的图像。 第二行(正图像)比第三行(负图像)更像是请求图像。
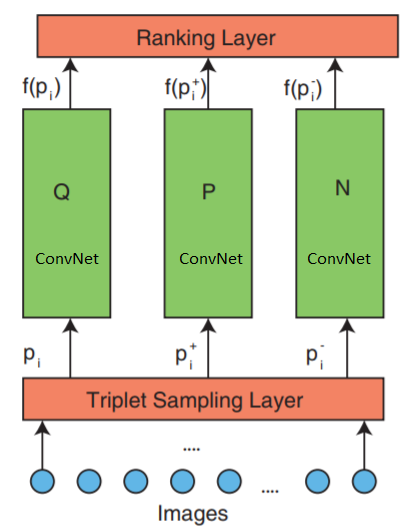
深度排名网络架构
该网络由3部分组成:三重采样,ConvNet和排名层。
网络接受三张图像作为输入。 一个图像三元组包含一个请求图像
$内联$ p_i $内联$ 正面形象
$内联$ p_i ^ + $内联$ 和负面形象
$ inline $ p_i ^-$ inline $ 它们独立地传输到三个相同的深度神经网络。
最顶层的层-评估三元组损失函数。 为了最小化损失函数,在较低层中纠正了该错误。
现在让我们仔细看一下中间层:
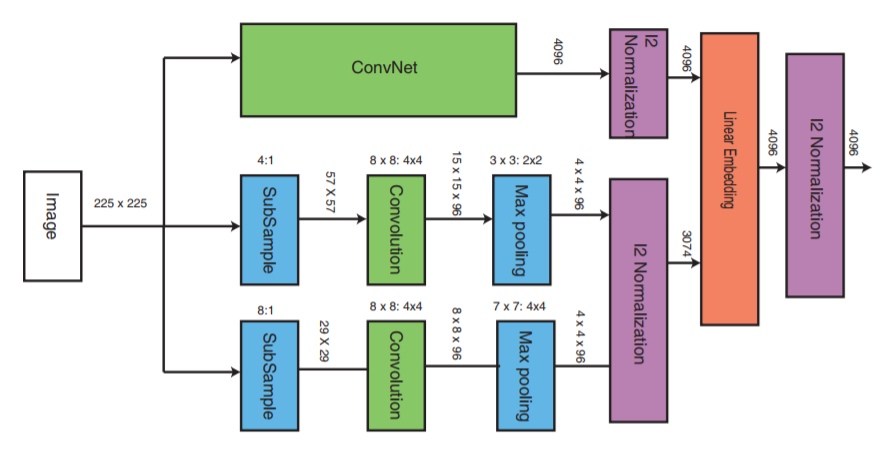
ConvNet可以是任何深度神经网络(本文将讨论卷积神经网络VGG16的实现之一)。 ConvNet包含卷积层,最大池层,本地规范化层和完全连接的层。
其他两个部分以降低的采样率接收图像,并执行卷积阶段和最大池化。 接下来,进行这三个部分的归一化阶段,最后将它们与线性层合并,随后进行归一化。
三重态形成
有多种方法可以创建三元组文件,例如,使用专家评估。 但是本文将使用以下算法:
- 类中的每个图像都构成一个请求图像。
- 除请求图像外,每个图像都将形成正图像。 但是您可以限制每个图像请求的正图像数量
- 从不是请求图像类别的任何类别中随机选择一个负图像
三重损失功能
目标是训练一种功能,该功能为最相似的图像分配一个较小的距离,为不同的图像分配一个较大的距离。 可以表示为:
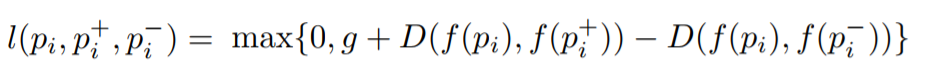
其中
l是三元组的损耗系数,
g是两对图像之间距离之间的间隙系数:(
$内联$ p_i $内联$ ,
$内联$ p_i ^ + $内联$ )和(
$内联$ p_i $内联$ ,
$ inline $ p_i ^-$ inline $ ),
f-将图片显示在矢量中的嵌入功能,
$内联$ p_i $内联$ 是请求的图像,
$内联$ p_i ^ + $内联$ 是正面形象,
$ inline $ p_i ^-$ inline $ 是负像,
D是两个欧几里得点之间的欧几里得距离。
深度排名算法实现
与Keras一起实施。
三个并行网络用于查询正图像和负图像。
该实现包括三个主要部分:
- 三种并行多尺度神经网络的实现
- 损失函数的实现
- 三重态产生
学习三个并行的深度网络将消耗大量的内存资源。 代替接收请求图像,正图像和负图像的三个并行深度网络,这些图像将被顺序地馈送到神经网络输入处的一个深度神经网络。 传递到损失层的张量将在每行中包含一个图像附件。 每行对应于分组中的每个输入图像。 由于请求图像,正图像和负图像是顺序发送的,因此第一行将与请求图像相对应,第二行将与正图像相对应,第三行将与负图像相对应,然后重复直到包结束。 因此,排名层接收所有图像的嵌入。 之后,计算损失函数。
要实现排名层,我们需要编写自己的损失函数,该函数将计算请求图像和正图像之间的欧几里得距离,以及请求图像和负图像之间的欧几里得距离。
损失计算功能的实现_EPSILON = K.epsilon() def _loss_tensor(y_true, y_pred): y_pred = K.clip(y_pred, _EPSILON, 1.0-_EPSILON) loss = tf.convert_to_tensor(0,dtype=tf.float32)
数据包大小应始终为3的倍数。由于三元组包含3张图像,并且三元组图像按顺序传输(我们将每个图像按顺序发送到深度神经网络)
其余代码在这里