动态编程以您在大学学习的方法而著称，然后仅在面试时记得。 但实际上，该方法适用于许多情况。 实际上，这是一种有效解决问题的技术，可以将其分为许多高度重复的子任务 。

在本文中，我将展示动态编程的一个有趣的实际应用-接缝雕刻任务。 该任务和方法在Avidan和Shamir的工作中作了详细描述， “为根据内容调整图像大小的接缝” （公共领域的文章）。

这是有关动态编程的系列文章之一。 如果您想重温方法，请参见图示的动态编程简介 。

根据内容调整图像大小

为了使用动态编程解决实际问题，您需要正确地制定公式。 本节介绍了所选任务的必要预设。

原始文章的作者描述了面向内容的图像大小调整，即基于内容更改图像的宽度或高度。 有关详细信息，请参见原始工作。我将进行简要概述。 假设您要调整冲浪者照片的大小：


冲浪者的顶视图在风平浪静中间的，有在右边的动荡波浪的。 照片： 基里尔·多布雷夫· Pixabay上的免费照片

如文章中详细描述的，有几种减小图像宽度的方法：这些是标准的裁剪和缩放，具有其固有的缺点，并且从中间去除了像素列。 可以想象，这在照片中留下了可见的接缝，而左右图像不匹配。 这样，您只能删除数量有限的图像。


尝试通过修整左侧并从中间切出块来减小宽度。 后者留下可见的接缝。

文章中的Avidan和Shamir描述了“接缝雕刻”的新技术。 它首先识别不太重要的“低能耗”区域，然后计算穿过图片的低能耗“接缝”。 在减小图像的宽度的情况下，确定从图像的顶部到底部的垂直接缝，其在每一行上向左或向右移动不超过一个像素。

在冲浪者的照片中，能量最低的接缝贯穿图像的中间，那里的水最安静。 这符合我们的直觉。


在冲浪者图像中发现的最低能量接缝显示为可见度为5个像素宽的红线，尽管实际上接缝仅为1个像素宽。

确定了能量最少的接缝，然后将其移除，我们将图像宽度减小了一个像素。 一遍又一遍地重复此过程会大大减小整个照片的宽度。


宽度减少1024像素后的冲浪者图像

再次，该算法从逻辑上去除了中间以及照片左侧的静止水。 但是与耕种不同，左侧的水的质地得以保留，并且没有急剧的过渡。 确实，您可以在中心找到一些不完美的过渡，但是基本上结果看起来很自然。

图像能量定义

魔术是找到最低能量的接缝。 为此，我们首先将能量分配给图像中的每个像素。 然后，我们使用动态程序设计以最小的能量找到穿过图像的路径-该算法将在下一部分中详细讨论。 首先，让我们看一下如何分配像素能量值。

该科学文章讨论了几种能量函数及其差异。 我们不要使其复杂化，而要使用一个函数来简单捕获每个像素周围的颜色变化量。 为了使图片更完整，如果您想自己实现它，我将更详细地描述能量函数，但这只是后续动态编程计算的预设。


左侧是从暗到亮的三个像素。 第一个和最后一个之间的差异很大。 右侧的三个暗像素，颜色强度略有不同

要计算特定像素的能量，请查看其左侧和右侧的像素。 在分量方面，我们计算它们之间的距离的平方，即红色，绿色和蓝色分量之间的差异的平方，然后将它们相加。 我们对中心上方和下方的像素执行相同的操作。 最后，将水平和垂直距离相加。

$$

$$| \ Delta x | ^ 2 =（\ Delta r_x）^ 2 +（\ Delta g_x）^ 2 +（\ Delta b_x）^ 2$$

$$

$$| \ Delta y | ^ 2 =（\ Delta r_y）^ 2 +（\ Delta g_y）^ 2 +（\ Delta b_y）^ 2$$

$$

$$e（x，y）= | \ Delta x | ^ 2 + | \ Delta y | ^ 2$$

唯一需要注意的是-如果像素在左侧边缘，则左侧没有相邻像素。 在这种情况下，我们仅与正确的像素进行比较。 对上边缘，右边缘和下边缘的像素执行类似的检查。

如果相邻像素的颜色差异很大，则能量函数很大；如果相邻像素的颜色相似，则能量函数很小。


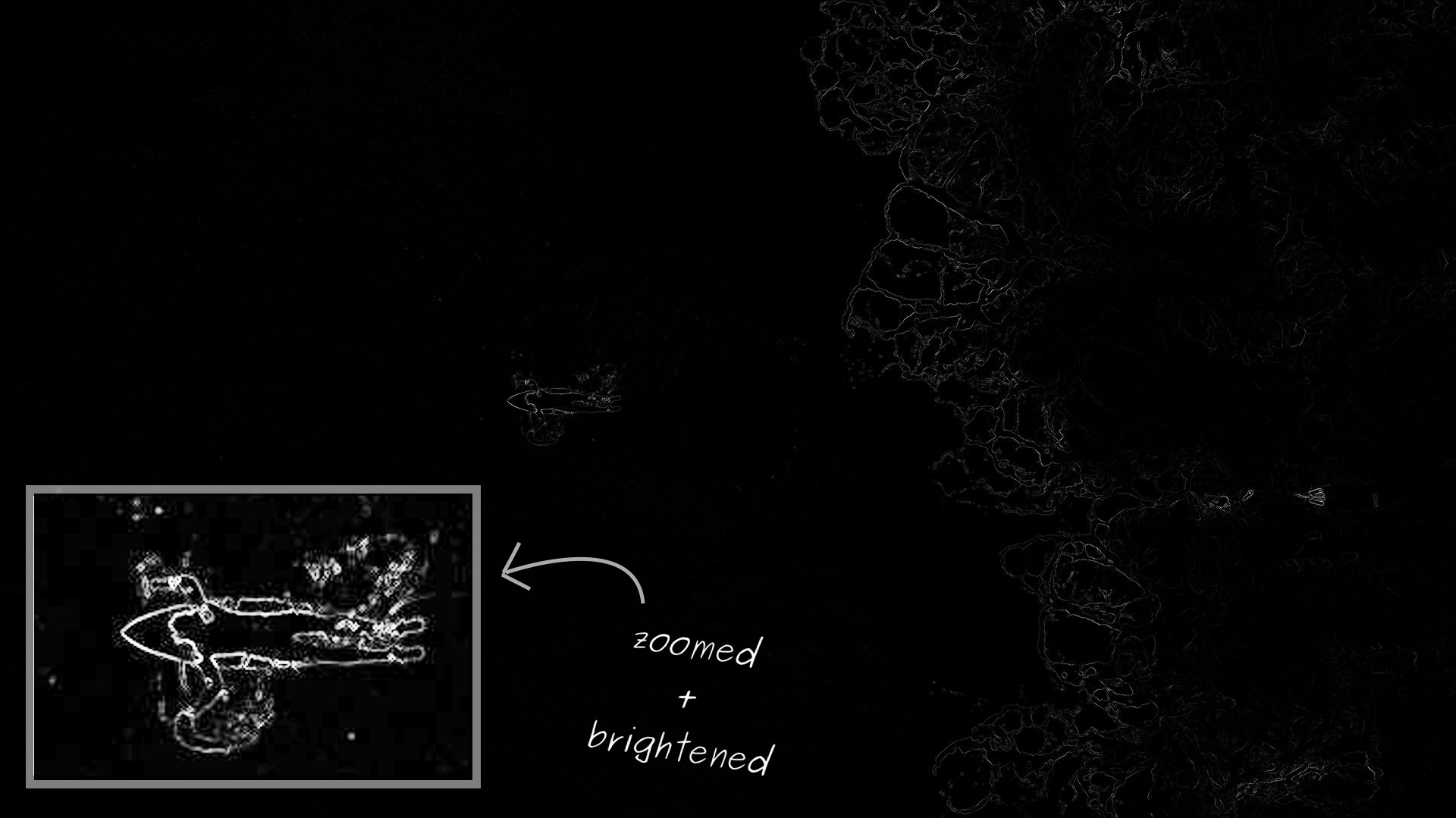冲浪者照片中每个像素的能量：较亮-越高。 不出所料，冲浪者在右侧的中波和湍流中具有最高的能量

能量功能在冲浪者照片上效果很好。 但是，它需要非常广泛的值。 因此，在渲染时，似乎在大多数照片中像素的能量为零。 实际上，与具有最高能量的区域相比，仅存在非常低的值。 为了简化可视化，我放大了冲浪者并突出显示了该区域。

通过动态编程搜索低能耗接缝

通过计算每个像素的能量，我们可以找到从图像顶部到底部能量最低的接缝。 相同的分析适用于水平接缝以减小原始图像的高度。 但是，我们将专注于垂直领域。

让我们从定义开始：

• 接缝是一系列像素，每行一个像素。 要求是连续两行之间的坐标 $$$x$ 变化不超过一个像素。 这样可以保留接缝顺序。
  
• 具有最低能量的接缝是其接缝中所有像素上的总能量最小化的接缝。

重要的是要注意，能量最低的关节不一定会穿过能量最低的所有像素。 考虑了全部而不是单个像素的总能量。


贪婪的方法行不通。 在早期选择低能量像素，我们会陷入图像的高能量区域（右侧的红色路径）

如您所见，您不能只选择下一行中能量最低的像素。

我们将问题分解为子任务

贪婪方法的问题在于，在决定下一步时，我们没有考虑到其余的缝隙。 我们不能展望未来，但我们能够考虑到目前已经知道的一切。

让我们将任务颠倒过来。 与其在几个像素之间进行选择以继续一个接缝，我们不如在几个接缝之间进行选择以转到一个像素 。 我们需要做的是获取每个像素，然后在上一行的像素之间进行选择，接缝可以从该像素中得出。 如果上面一行中的每个像素都编码了到达此点的路径，那么我们实质上是在查看到此点的完整历史记录。


对于每个像素，我们在上面的行中研究三个像素。 基本选择-哪些接缝可以继续？

假定图像中每个像素都有一个子任务。 子任务应该找到通往特定像素的最佳路径，因此，最好将每个像素的低能量接缝的能量与该像素相关联。

与贪婪方法不同，上述方法本质上尝试通过图像的所有可能路径。 只是当检查所有可能的路径时，一次又一次地解决了相同的子任务，这使该方法成为动态编程的理想选择。

递归关系的定义

像往常一样，现在我们需要以递归关系形式将想法正式化。 原始图像中的每个像素都有一个子任务，因此我们递归关系的输入可以只是坐标 $$$x$ 和 $$$y$ 这个像素 这提供了整数输入，使组织子任务变得容易，并且能够将先前计算的值存储在二维数组中。

定义功能 $$$M（x，y）$ ，代表能量最小的垂直煤层的能量。 它从图像的顶部开始，以像素为结尾 $$$（x，y）$ 。 职称 $$$M$ 如原始科学文章中所选择。

首先，您需要一个基本版本。 在最上面一行结束的所有接缝的长度只有一个像素。 因此，具有最小能量的接缝只是具有最小能量的像素：

$$

$$M（x，0）= e（x，0）$$

对于其余行中的像素，请查看顶部的像素。 由于接缝应该是连续的，因此我们只考虑位于左上，右上和右上的三个像素。 从它们中，我们选择能量最低的接缝，该接缝以这些像素之一结尾，然后加上当前像素的能量：

$$

$$M（x，y）= e（x，y）+ \ min \ begin {cases} M（x-1，y-1）\\ M（x，y-1）\\ M（x + 1， y-1）\结尾{cases}$$

作为边界情况，请考虑当前像素位于图像的左边缘或右边缘的情况。 在这些情况下，我们省略 $$$M（x-1，y-1）$ 用于左边缘的像素或 $$$M（x + 1，y-1）$ 在右边。

最后，您需要提取低能量接缝的能量，该能量覆盖图像的整个高度。 这意味着我们查看图像的底线并选择以这些像素之一结尾的最低能量的接缝。 对于宽幅照片 $$$W$ 又高 $$$H$ 像素：

$$

$$\ min_ {0 \ le x <W} M（x，H-1）$$

因此，我们获得了具有所有必要属性的递归关系：

• 递归关系具有整数输入。
  
• 最终答案很容易从关系中提取。
  
• 比例取决于自己。

验证DAG子任务（面向非循环图）

由于每个子任务 $$$M（x，y）$ 对应于原始图像的一个像素，相关性图非常容易可视化。 只需将它们放置在二维网格上即可，就像原始图像一样！


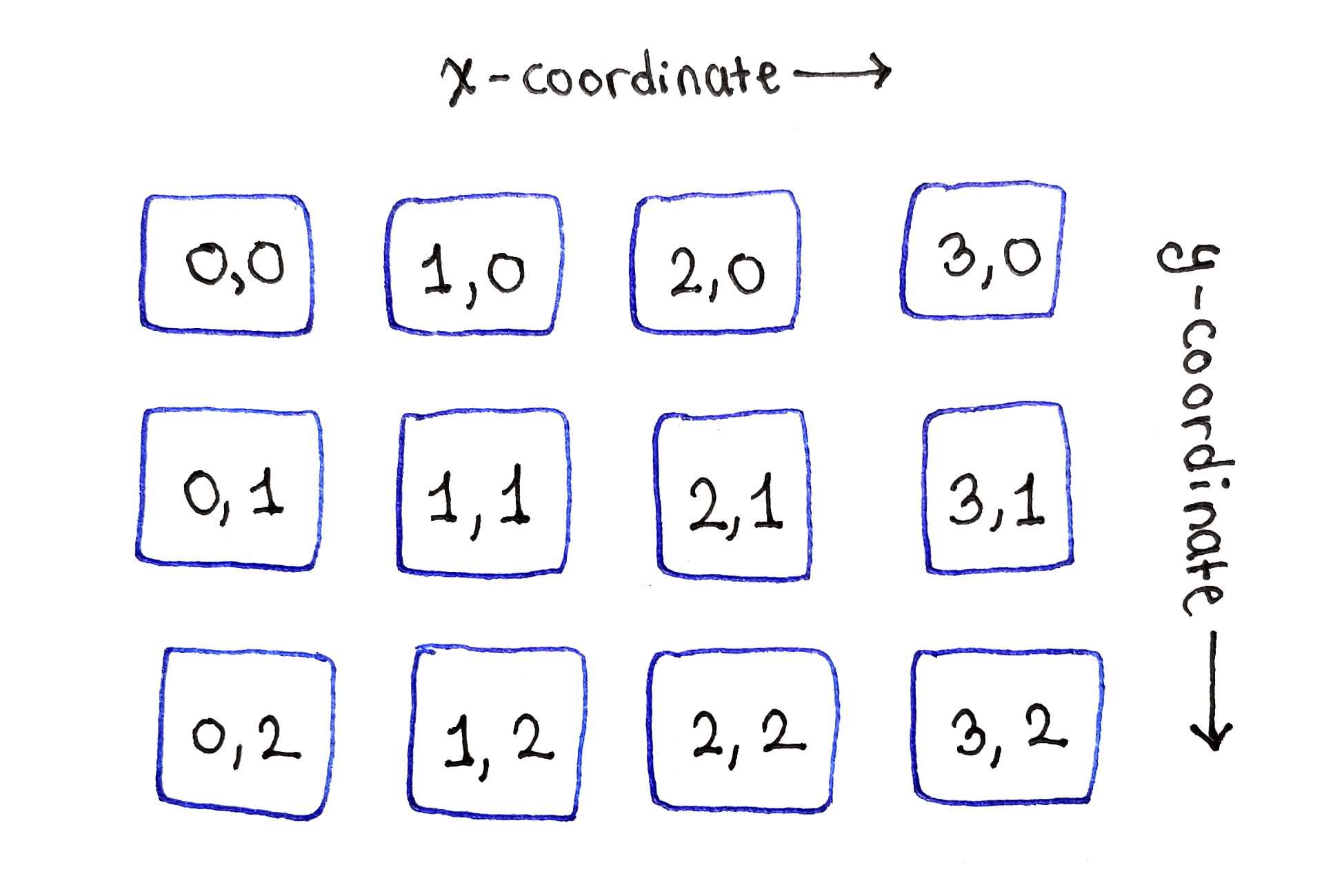子任务位于二维网格中，就像原始图像中的像素一样

从循环关系的基本方案中可以看出，可以使用各个像素的能量值来初始化子任务的顶行。


第一行独立于其他子任务。 请注意没有从顶部的单元格的箭头

第二行开始显示依赖关系。 首先，在第二行最左边的单元格中，我们面临着边界局势。 由于左侧没有单元格，因此该单元格 $$$（1,0）$ 仅取决于位于其正上方和右上方的单元格。 稍后第三行中最左边的单元格也会发生相同的情况。


左侧边缘上的子任务仅取决于它们上方的两个子任务

在第二行（1,1）的第二个单元格中，我们看到了递归关系的最典型表现。 此单元格取决于三个单元格：左上方，上方上方和右上方。 此依存关系结构适用于第二行和后续行中的所有“中间”单元格。


左右边缘之间的子任务取决于顶部的三个子任务

最后，右边的单元格代表第二个边界情况。 由于右侧没有更多的单元格，因此仅取决于直接位于顶部和左侧的单元格。


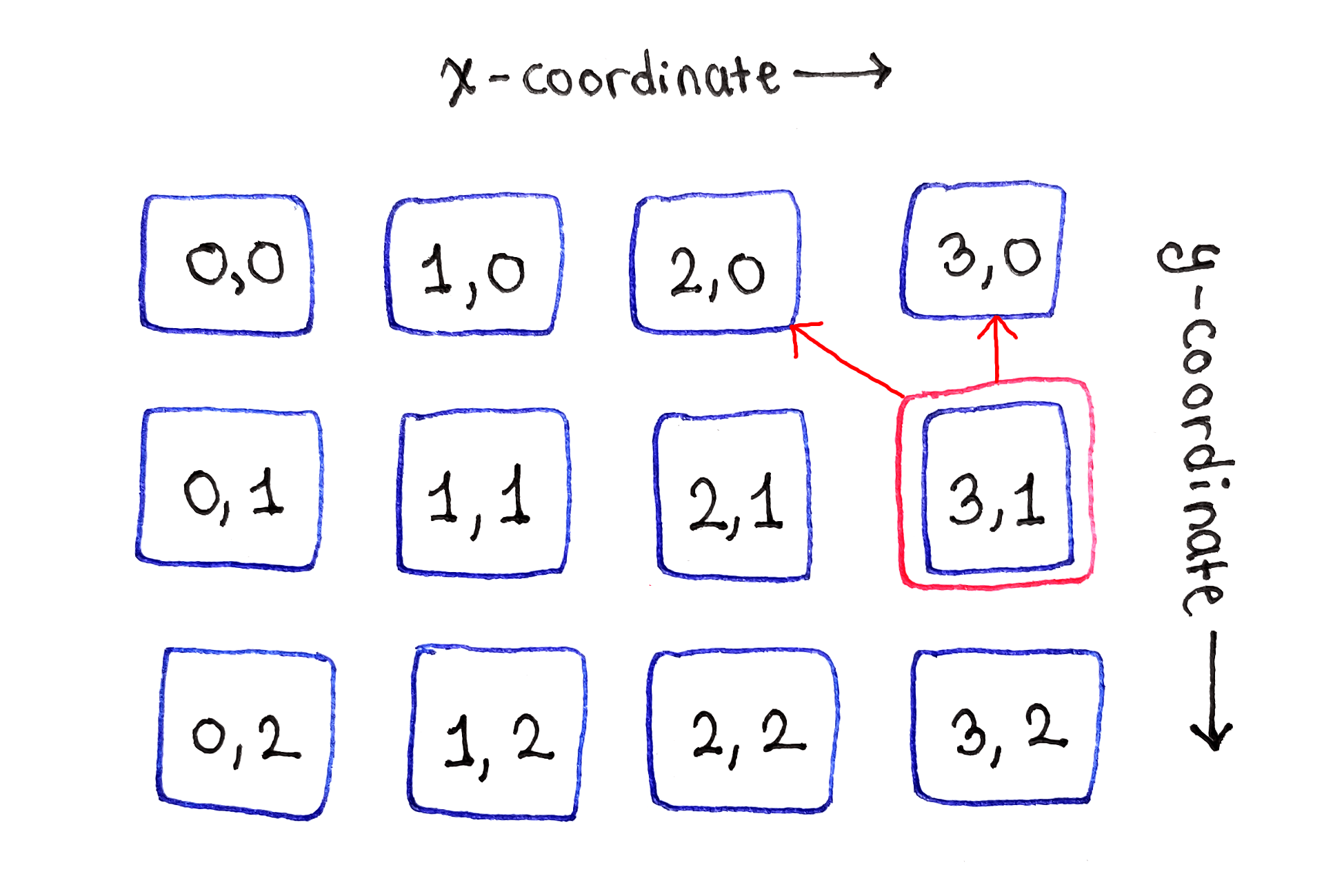右侧的子任务仅取决于顶部的两个单元

对所有后续行重复此过程。


由于依赖性图中有许多箭头，因此此动画依次显示了每个子任务的依赖性

完整的依存关系图会让您感到迷惑，但同时查看一次箭头有助于建立明确的模式。

自下而上的实施

进行分析后，我们得到了加工订单：

• 从图像的顶部到底部。
  
• 每行可以按任何顺序执行。 自然的选择是从左到右。

由于每一行仅依赖于前一行，因此您只需要保存两行数据：一行用于上一行，一行用于当前行。 从左向右移动，我们甚至可以丢弃使用前一行中的各个元素。 但是，这使算法复杂化，因为它必须找出可以丢弃前一行的哪些部分。

在下面的Python代码中，输入是行列表，其中每行包含一个数字列表，这些数字表示该行中的各个像素能量。 输入称为pixel_energies ， pixel_energies[y][x]表示坐标中的像素能量 $$$（x，y）$ 。

让我们开始计算上一行接缝的能量，只需复制上一行的各个像素能量即可：

 previous_seam_energies_row = list(pixel_energies[0]) 

然后，我们循环遍历其余输入线，计算每条线的接缝能量。 最“困难”的部分是确定要引用上一行的哪些元素，因为左边缘左侧或右边缘右侧没有像素。

在每次迭代中，将为当前线创建一个新的缝线能量列表。 在迭代结束时，我们将前一行的数据替换为下一次迭代的当前行的数据。 这是我们丢弃前一行的方式：

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_seam_energy = pixel_energy + \ min(previous_seam_energies_row[x_i] for x_i in x_range) seam_energies_row.append(min_seam_energy) previous_seam_energies_row = seam_energies_row 

结果， previous_seam_energies_row包含底线的接缝能量。 我们在此列表中找到最小值-这就是答案！

 min(seam_energy for seam_energy in previous_seam_energies_row) 

您可以通过将代码包装在一个函数中，然后用您构建的二维数组调用它来测试此实现。 选择以下输入以使贪婪方法失败，并且接缝明显且能量最低：

 ENERGIES = [ [9, 9, 0, 9, 9], [9, 1, 9, 8, 9], [9, 9, 9, 9, 0], [9, 9, 9, 0, 9], ] print(min_seam_energy(ENERGIES)) 

时空复杂度

原始图像中的每个像素对应一个子任务。 对于每个子任务，不超过三个依赖项，因此解决每个子任务都需要进行大量的工作。 最后一行保持两次。 因此对于整个图像 $$$W$ 又高 $$$H$ 像素时间复杂度为 $$$O（宽×高+宽）$ 。

在每个时间点，我们都有两个列表：一个用于上一行，一个用于当前。 在第一 $$$W$ 元素，第二个逐渐增加到 $$$W$ 。 因此，空间复杂度等于 $$$O（2W）$ 那只是 $$$O（w）$ 。

请注意，如果实际上丢弃了前一行的数据元素，则将以与当前行的列表增长相同的速度缩短前一行的元素列表。 因此，空间复杂度将保持 $$$O（w）$ 。 尽管宽度可能有所不同，但这通常并不那么重要。

低能耗向后指针

因此，我们找到了低能耗煤层的含义，但是如何处理这些信息？ 毕竟，实际上，我们不是在关注能源的重要性，而是在接缝本身！ 问题在于，无法从最后一个像素返回到接缝的其余部分。

这是我在前几篇文章中遗漏的，但是对于许多动态编程问题也是如此。 例如，如果您还记得抢劫房屋的任务 ，我们发现了抢劫金额的最大值，但没有找到需要抢劫特定房屋的金额。

反向指针的表示

一般回答：存放指针 。 在切割接缝的任务中，我们不仅需要每个像素处的接缝能量值。 您还需要知道前一行中的哪些像素导致了这种能量。 通过存储此信息，我们可以沿反向指针一直到顶行，以最少的能量获取组成关节的所有像素的坐标。

首先，创建一个用于存储能量和后向指针的类。 能量将用于计算子任务。 由于后向指针确定了前一行中的哪个像素提供了当前能量，因此我们可以简单地将其想象为x坐标。

 class SeamEnergyWithBackPointer(): def __init__(self, energy, x_coordinate_in_previous_row=None): self.energy = energy self.x_coordinate_in_previous_row = x_coordinate_in_previous_row 

每个子任务的计算结果不仅是数字，而且是此类的一个实例。

向后指针存储

最后，您需要沿着图像的整个高度返回，并按照相反的符号以最少的能量恢复接缝。 不幸的是，这意味着您需要存储图像中所有像素的指针，而不仅仅是前一行。

为此，我们只是保存所有子任务的全部结果，尽管在技术上可以拒绝前几行接缝的数值能量。 结果存储在二维数组中，该数组看起来与输入数组相同。

让我们从第一行开始，该行仅包含单个像素能量。 由于没有前一行，因此所有的后向指针都丢失了，但是为了保持一致，我们仍将存储SeamEnergyWithBackPointers实例：

 seam_energies = [] # Initialize the top row of seam energies by copying over the top row of # the pixel energies. There are no back pointers in the top row. seam_energies.append([ SeamEnergyWithBackPointer(pixel_energy) for pixel_energy in pixel_energies[0] ]) 

主循环的工作原理与以前的实现基本相同，但有以下区别：

• 前一行的数据包含SeamEnergyWithBackPointer实例，因此在计算重复率的值时，应在这些对象内寻找接缝的能量。
  
• 保存当前像素的数据，您需要构建SeamEnergyWithBackPointer的新实例。 在这里，我们将存储当前像素的接缝能量以及上一行的x坐标，用于计算当前接缝能量。
  
• 在每行的末尾，我们不会丢弃前一行的数据，而只是将当前行的数据添加到seam_energies 。

 # Skip the first row in the following loop. for y in range(1, len(pixel_energies)): pixel_energies_row = pixel_energies[y] seam_energies_row = [] for x, pixel_energy in enumerate(pixel_energies_row): # Determine the range of x values to iterate over in the previous # row. The range depends on if the current pixel is in the middle of # the image, or on one of the edges. x_left = max(x - 1, 0) x_right = min(x + 1, len(pixel_energies_row) - 1) x_range = range(x_left, x_right + 1) min_parent_x = min( x_range, key=lambda x_i: seam_energies[y - 1][x_i].energy ) min_seam_energy = SeamEnergyWithBackPointer( pixel_energy + seam_energies[y - 1][min_parent_x].energy, min_parent_x ) seam_energies_row.append(min_seam_energy) seam_energies.append(seam_energies_row) 

跟随标志

现在，整个子任务表已填满，我们可以用最少的精力恢复接缝。 我们从在底线中寻找x坐标开始，该坐标对应于能量最小的关节：

 # Find the x coordinate with minimal seam energy in the bottom row. min_seam_end_x = min( range(len(seam_energies[-1])), key=lambda x: seam_energies[-1][x].energy ) 

现在，从图像的底部转到顶部， $$$y$ 从len(seam_energies) - 1到零。 在每次迭代中，添加当前对 $$$（x，y）$ 到代表我们接缝的列表中，然后设置值 $$$x$ SeamEnergyWithBackPointer指向的对象在当前行中。

 # Follow the back pointers to form a list of coordinates that form the # lowest-energy seam. seam = [] seam_point_x = min_seam_end_x for y in range(len(seam_energies) - 1, -1, -1): seam.append((seam_point_x, y)) seam_point_x = \ seam_energies[y][seam_point_x].x_coordinate_in_previous_row seam.reverse() 

因此，接缝是向上构建的，如果需要从上到下的坐标，则可以以相反的顺序读取列表。

时空复杂度

时间复杂度与上一个相似，因为我们仍然需要处理每个像素一次。 在查看了最后一行并找到能量最少的关节之后，然后我们沿着图像的整个高度上升以恢复关节。 所以对于图像 $$$W×H$ 时间复杂度等于 $$$O（宽×高+宽+高）$ 。

至于数量，我们仍然为每个子任务保留恒定数量的数据，但是现在我们不丢弃任何数据。 所以我们用音量 $$$O（宽×高）$ 。

低能耗接缝去除

一旦找到能量最低的垂直关节，我们就可以简单地将像素从原始图像复制到新图像。 新图像的每一行都包含原始图像相应行中的所有像素，但接缝中具有最低能量的像素除外。 由于我们从图像开始每行删除一个像素 $$$W×H$ 然后我们得到图像 $$$（W − 1）×H$ 。

我们可以通过重新计算新图像中的能量函数并在其上找到最低能量的接缝来重复此过程。 似乎很想在原始图像中找到多个低能耗接缝，然后立即将其全部删除。 问题是两个接缝可以相交。 删除第一个像素后，第二个像素将无效，因为它缺少一个或多个像素。


去除接缝过程的动画。 最好全屏观看，以使接缝更清晰

视频的每一帧都是每次迭代时的图像，具有最小能量的接缝叠加可视化。

另一个例子

这篇文章有很多详细的解释，所以让我们以一系列美丽的照片作为结尾！ 下图显示了拱门国家公园的岩层：


与一个孔的岩层在拱门国家公园。 照片： Flickr上的 Mike Goad

此图像的能量函数：


照片中每个像素的能量：越亮-越高。 注意孔边缘周围的高能量。

作为计算的结果，获得了具有最低能量的这种接缝。 请注意，它穿过右侧的岩石，直接进入岩石层，岩石顶部的照明部分与天空的颜色匹配。 也许您应该选择更好的能量功能！


图像中发现的最低能量接缝以5像素宽的红线显示，以提高可见度，尽管实际上接缝只有1像素宽。

最后，调整大小后的拱门图像：


1024像素压缩后的拱

结果肯定不是完美的：原始图像上的山峰许多边缘都变形了。 改进之一可能是实现科学文章中列出的其他能源功能之一。

---

尽管通常在理论上讨论动态编程，但它是解决复杂问题的有用实用方法。 在本文中，我们研究了动态编程的一种应用：通过切割接缝来调整图像大小以适合内容。

我们应用了相同的原理，将问题分为较小的子任务，分析了这些子任务之间的依赖关系，然后以最小化算法的空间和时间复杂度的顺序解决了子任务。 此外，我们研究了使用反向指针不仅找到最佳接缝的能量值，而且还确定组成该值的每个像素的坐标。 然后，我们将这些部分应用于一个实际问题，该问题需要进行一些预处理才能真正有效地使用动态编程算法。