引言
1937年,美国石窟Reber建造的第一批射电望远镜之一。 射电望远镜是一个直径9.5 m的锡镜,安装在木框上:

到1944年,雷伯(Reber)编制了第一张银河系区域空间无线电波分布图。
射电天文学的发展涉及许多发现:1946年,发现了天鹅座星座的无线电辐射; 1951年发现了银河系外辐射; 1963年发现了类星体; 1965年发现了波长为7.5 cm的遗迹本底辐射。
1963年,在阿雷西博(波多黎各)建造了独特的300米射电望远镜。 这是一个带有移动辐射器的固定碗,内置在地形的自然裂缝中。

单射射电望远镜的角分辨率很小,由以下公式确定:
Theta= frac lambdad在哪里
lambda -波长
d -射电望远镜的直径。
显然,为了提高分辨率,必须增加天线的直径,这在物理上是一项艰巨的任务。 随着无线电干涉仪的出现,有可能解决这个问题。
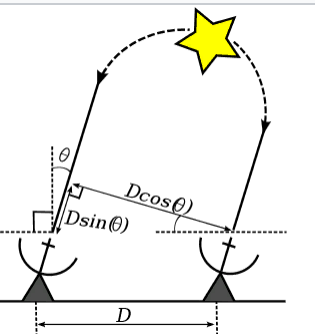
靠近地球的遥远恒星发出的电磁波的前部可以认为是平坦的。 对于由两个天线组成的最简单的干涉仪,到达这两个天线的光线的路径差将等于:
Delta=D cdotsin( Theta) ,
其中:
\三角洲 -光线的差异;
D -天线之间的距离;
Theta -射线的到达方向与天线所在的法线之间的夹角。
在
Theta=0 到达两个天线的电波相加。 在反相时,在以下情况下首先出现波:
Delta= frac lambda2, Theta=arcsin frac lambda2D ,
其中:
lambda -波长。
下一个最大值将是
Delta= lambda, 最低
Delta= frac3 lambda2 等。获得了多瓣辐射图(DN),其主瓣的宽度为
lambda<<D 等于
lambda/D 。 主瓣的宽度决定了无线电干涉仪的最大角分辨率,它大约等于瓣的宽度。
超长基础射电干涉测量法(VLBI)是射电天文学中使用的一种干涉测量方法,其中干涉仪(望远镜)的接收元件之间的距离不比彼此之间的大陆距离近。
VLBI方法使您可以组合由多个望远镜进行的观测,从而模拟尺寸等于原始望远镜之间最大距离的望远镜。 VLBI的角分辨率比最佳光学仪器的分辨率大数万倍。
VLBI网络的当前状态
如今,一些VLBI网络正在监听太空:
- 欧洲–EVN(欧洲VLBI网络),由20多个射电望远镜组成;
- 美式–VLBA(超长基线阵列),包括十个直径为25米的望远镜;
- 日语-JVN(日本VLBI网络)由位于日本的十个天线组成,其中包括四个天文天线(VERA项目-VLBI射电占星术探索);
- 澳大利亚-LBA(长基线数组);
- 中文-CVN(中文VLBI网络),由四个天线组成;
- 韩国-KVN(韩国VLBI网络),其中包括三台21米射电望远镜;
- 俄罗斯人-基于永久性无线电干涉系统-配备直径32 m的射电望远镜的“ Kvazar-KVO”,配备了波长范围从1.35 cm到21 cm的高度灵敏的低温辐射仪。东西方(见图)。
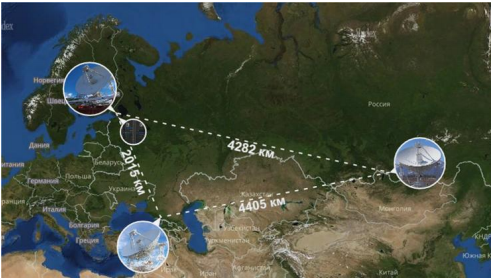
在VLBI复合物“ Kvazar-KVO”中,氢标准用作所有频率转换的参考频率源,这些频率转换使用氢原子基态的超精细结构的能级之间的转换,频率为1420.405 MHz,相当于射电天文学的21 cm。
通过VLBI解决的任务
- 天体物理学 构造自然空间物体(类星体和其他物体)的无线电图像时,其分辨率为十分之一和百分之一百的质量(毫秒)。
- 占星术研究。 协调时间系统的构建。 研究的对象是角度尺寸极小的无线电源,包括准星无线电源和无线电星系核,由于它们的遥远性,它们几乎是创建支持固定物体网络的理想对象。
- 研究天体力学和太阳系动力学,太空导航。 在行星表面上安装信标并跟踪行星际自动站的信标,使得可以使用VLBI方法来研究诸如行星的轨道运动,旋转轴的方向及其进动,卫星地球系统动力学等参数。 对于月球而言,确定物理解放和确定月地球系统动力学的非常重要的问题也正在解决。
使用VLBI在太空中导航
- 1971年监视宇航员在月球表面的运动。他们在罗孚(Rover)月球车的帮助下进行了运动。 确定其相对于月球组件的位置的精度达到20厘米,并且主要取决于月亮的释放(振动-月亮相对于其质心的周期性摆状振荡);
- 为从空中飞行器向金星大气中传送和释放浮空探测器提供导航支持(VEGA项目)。 距金星的距离超过1亿公里,发射器功率仅为1瓦。 VEGA-1 / 2发射于1984年12月进行。1985年6月11日至15日,气球被放到金星的大气中。观测进行了46个小时。
简化的VLBI网络的结构图
基于真实的VLBI网络,使用Python软件,我们以每个单元或过程的单独模型的形式对简化的VLBI系统进行建模。 这套模型足以观察基本过程。 图中显示了简化的VLBI网络的结构图:
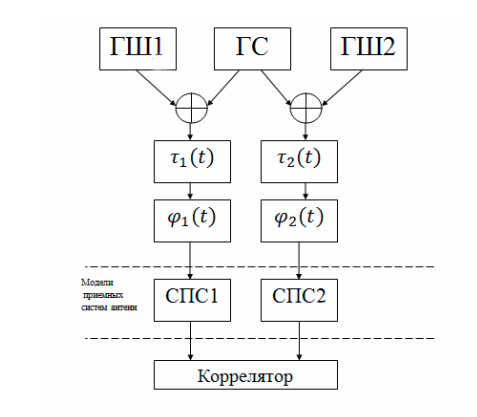
该系统包括以下组件:
- 发生器有用的调相信号(HS);
- 噪声发生器(GSh1,GSh2)。 该系统有两个具有自身噪声的射电望远镜(接收天线)。 此外,还有大气噪声以及其他自然和人工的无线电发射源;
- 时间延迟单元,模拟由于地球自转而线性变化的时间延迟;
- 模拟多普勒效应的移相器;
- 信号转换系统(SPS),由一个用于将信号向下频率转换的本地振荡器和一个带通滤波器组成;
- FX相关器。
相关器电路如下图所示:
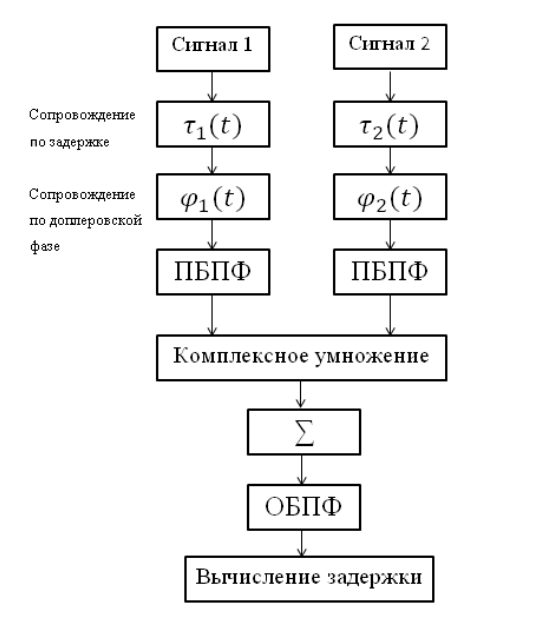
给定的相关器电路,包括以下模块:
- 直接快速傅立叶变换(PBPF)和逆傅立叶变换(OBPF);
- 补偿先前引入的延迟;
- 补偿多普勒效应;
- 两个光谱的复数乘法;
- 总结累积的实现。
导航信号模型
VLBI测量最方便的是卫星导航系统的航天器的导航信号,例如GPS和GLONASS。 对导航信号有许多要求:
- 允许您很好地定义伪距;
- 传输有关导航系统位置的信息;
- 有别于其他NS的信号;
- 请勿干扰其他无线电系统;
- 不需要复杂的设备进行接收和传输。
他们对具有二进制(两个位置)相位调制的信号-BPSK(二进制相移键)足够满意,在俄罗斯文献中将其称为FM-2。 此调制将载波振荡的相位改变π,可以表示为:
S(t)=A cdotG(t) cdotcos(2 pift),其中G(t)是调制函数。
为了实现相位调制,可以使用两个发生器,每个发生器形成相同的频率,但初始相位不同。 调制功能使您可以扩展信号的频谱并准确地测量伪距(卫星与接收器之间的距离,该距离由信号传播时间计算,而无需校正卫星与接收器之间的时钟差)。
这是解释BPSK基本原理的清单:
上市from scipy import* from pylab import* import numpy as np import scaleogram as scg f = 2;
我们得到:
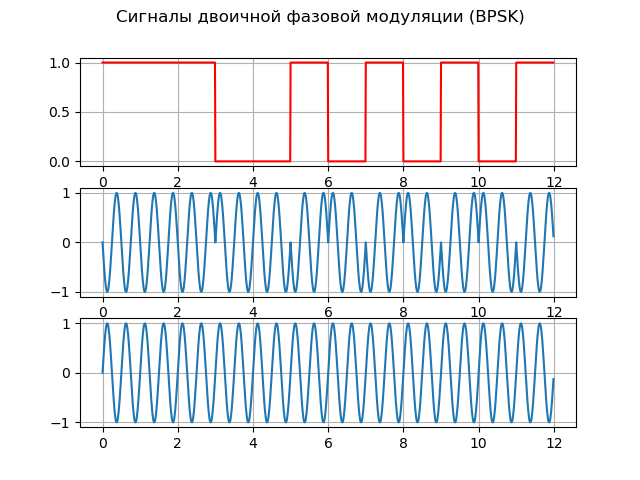
源模型
来自卫星或航天器的调相导航谐波信号具有以下形式:
x=a(2 pifct+ sumsncos(2 pifnt)),载波频率在哪里
fc=$8. GHz的
该信号具有几个受控参数:第n个调制振荡的幅度
sn, 它的频率
fc 和载波振荡的幅度a。
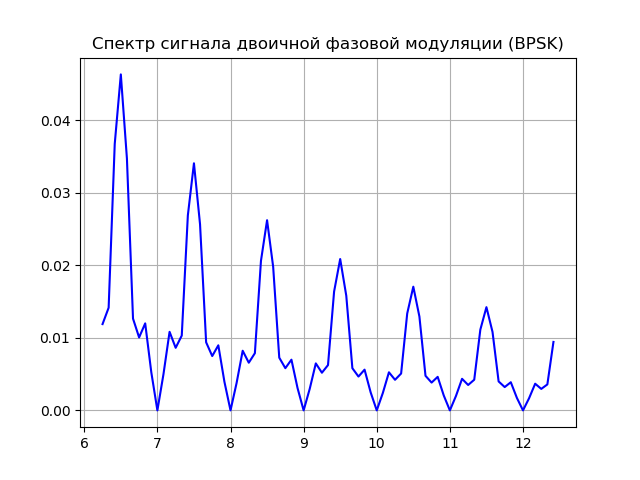
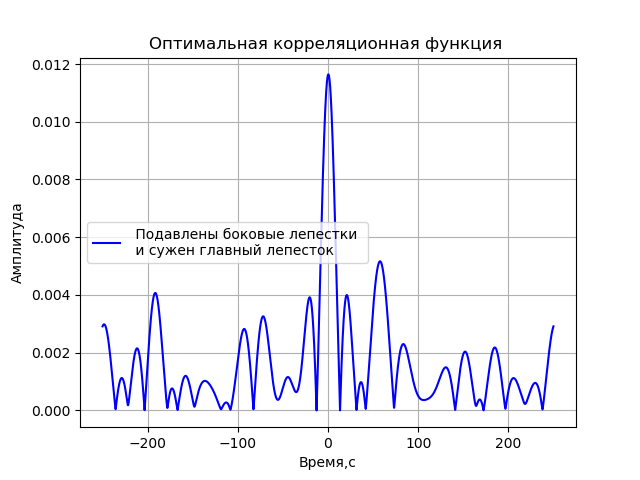
为了获得尽可能抑制旁瓣并达到最窄的相关峰的相关函数,我们将使用2、4、8和16 MHz的值以及从0到2π的范围内以π为增量的调制指数来改变频率值。 让我给您列出程序的清单,以搜索最终结果的调相函数的参数:
我们得到:
结果函数的形式为:
x=cos(2 pifct+2 picos(2 pi106t)+2 picos(2 pi108t)+4 picos(2 pi1016t))。(1)美此外,此功能将用于模拟VLBI。
噪声发生器模型,用于模拟与来自太空和地球大气层的信号一起接收到的干扰
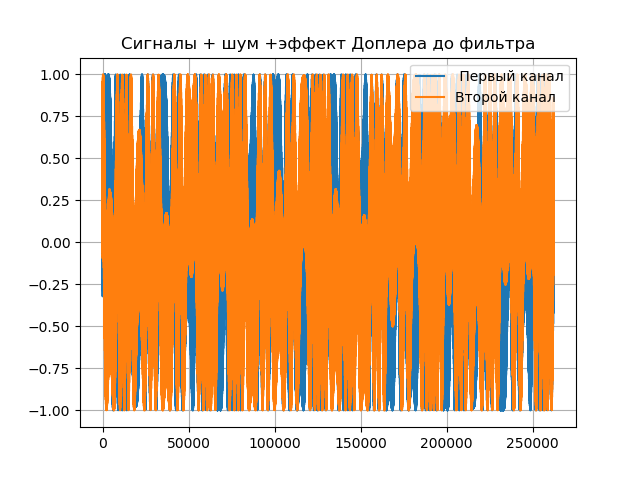
调相导航信号的功能(1)可以应用于无线电干涉仪的两个通道,但是有必要考虑第二个通道中的信号延迟和两个通道中的噪声,如下表所示:
我们得到:
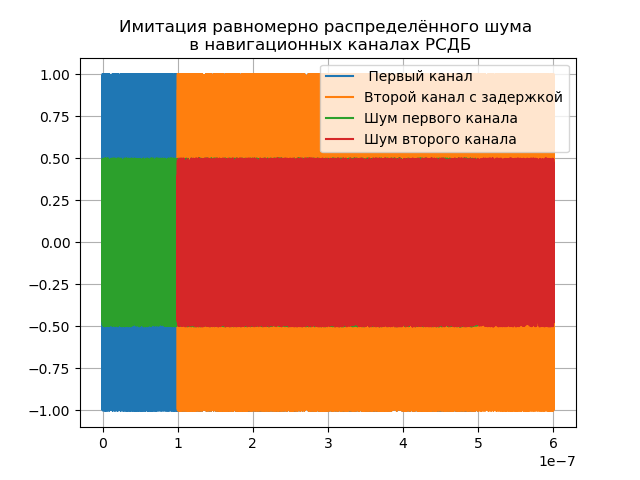
为演示设置了delay delay = 1e-7,实际上它取决于基准,可以达到四个或更多单位。
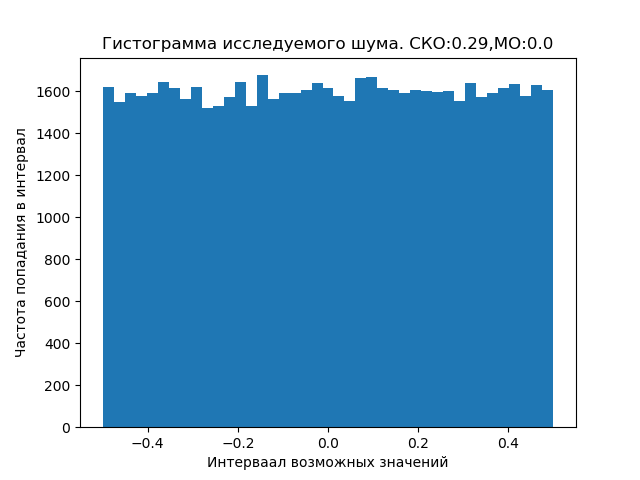
可以根据与给定制服不同的定律来分配宇宙噪声和近地噪声,这需要进行特殊研究。
建模多普勒效应
由于地球具有圆形形状并绕其轴旋转,因此来自太空的信号以不同的延迟到达天线。 因此,必须及时移动信号并考虑多普勒频率。 我们将近似地认为延迟根据线性定律而变化:
taux(t)=ax+bxt,(2)在哪里
ax=1..3 cdot10−3 毫秒和
bx=1..3 cdot10−6 毫秒 发现多普勒相位是延迟的导数:
fdx= fracd tau(t)dt=bx,(3)收到的信号应类似于:
hatx=x(t− taux)ej2 pifdxt,其中x(t)是航天器的辐射信号。
以下列表显示了多普勒效应的演示:
我们得到:
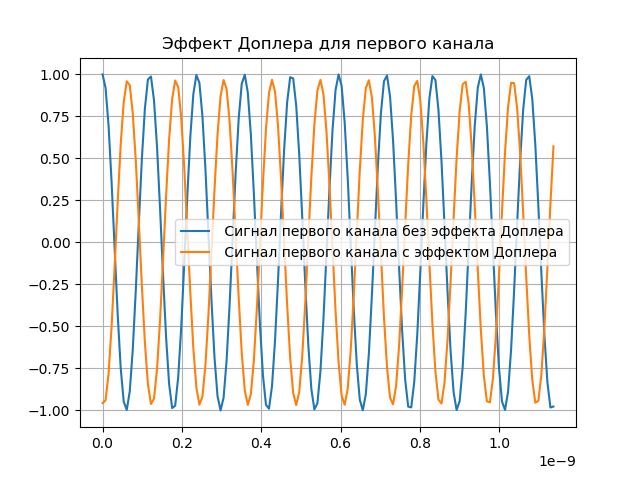
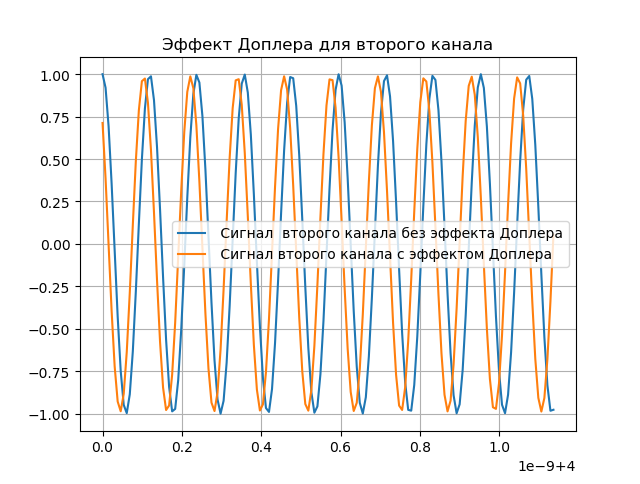
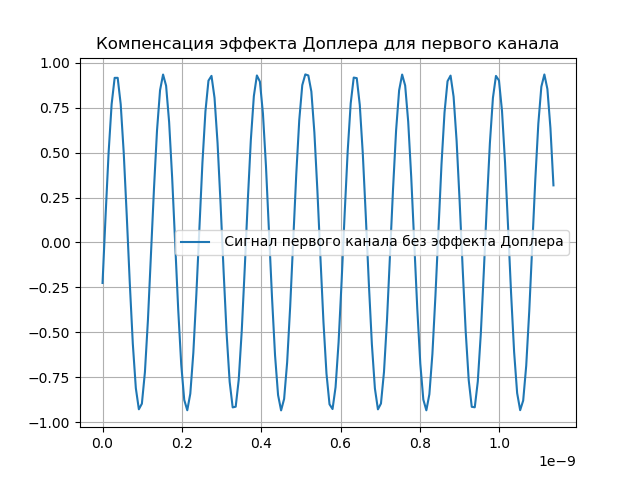
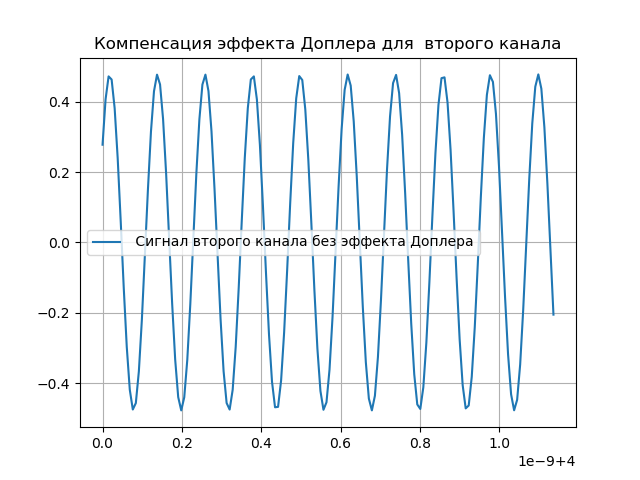
建模多普勒补偿
显然,必须补偿对信号的更改。 为此,系统包含对延迟和多普勒相位的支持。 信号通过注册系统后,会引入延迟:
tauex(t)=ax+bext,(4)它将考虑以一定的精度计算延迟,从而
\左|aex−ax\右|<30 ns
\左|bex−bx\右|<10 ns,即 这与他早些时候的拖延有所不同。 显然,延迟的引入与以前引入的符号相反。
收到的信号看起来像:
hatx=\波浪线x(t+ tauex)e−j2 pifdet。(5)多普勒效应补偿如下表所示:
我们得到:
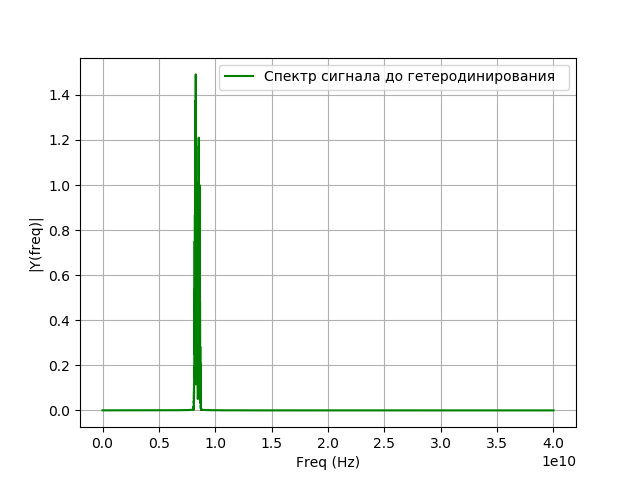
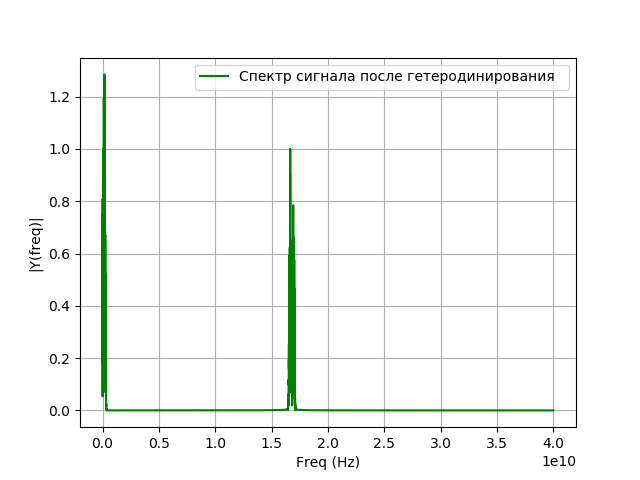
信号外差仿真
信号进入配准系统后,将发生频率转换,也称为外差。 这是一种非线性变换,其中两个不同频率的信号
f1 和
f2 差频信号突出显示-
f=\左|f1−f2\对。 本地振荡器信号的频率将等于被调查信号的频率与传输后要获得的频率之间的差。 使用谐波振荡的辅助发生器(本机振荡器和非线性元件)进行外差。 在数学上,外差是信号与指数的乘积:
xg=\帽子xej2 pifgt,(6)在哪里
fg -本地振荡器信号。
外差程序:
我们得到:
外差后建模信号滤波
外差后,信号进入带通滤波器。 滤波器通带(PP)
fpass=32 兆赫 使用signal.firwin库函数通过窗口方法计算滤波器的脉冲响应。 为了在滤波器的输出处获得信号,在时域中对滤波器和信号进行卷积。 对于我们的情况,卷积积分的形式为:
checkx(t)= int+ infty− inftyxg(t)h(t−t′)dt,(7)其中,h(t)是滤波器的脉冲响应。
使用signal.convolve库函数可以找到卷积。 考虑到外差和滤波的配准信号以公式的形式表示
checkx(t)=( hatx(t)e−j2 pifgt)∗h用*表示卷积。
建模过滤程序:
我们得到:
用于VLBI的数字信号转换器主要使用具有有限冲激响应(FIR)的滤波器,因为与具有无限冲激响应(IIR)的滤波器相比,它们具有许多优点:
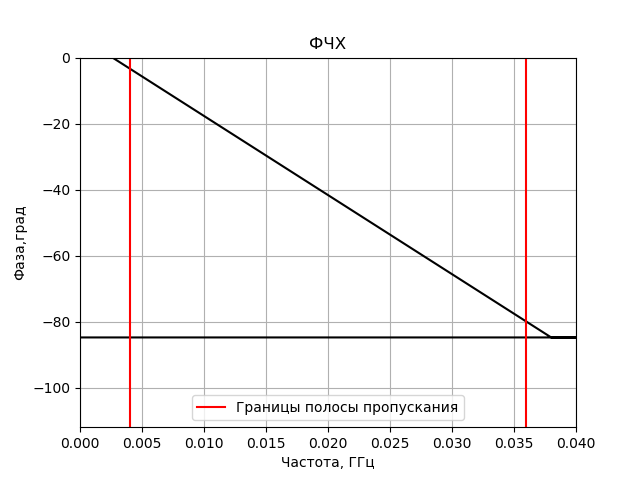
- 在脉冲响应(IM)对称的情况下,FIR滤波器可能具有严格的线性相位响应。 这意味着使用这种滤波器可以避免相位失真,这对于无线电干涉仪而言尤其重要。 具有无限脉冲响应(IIR)的滤波器不具有THEM的对称特性,并且不能具有线性相位响应。
- FIR滤波器是非递归的,这意味着它们始终是稳定的。 不能总是保证IIR滤波器的稳定性。
- 对于FIR滤波器,使用有限数量的位来实现滤波器的实际后果明显不那么重要。
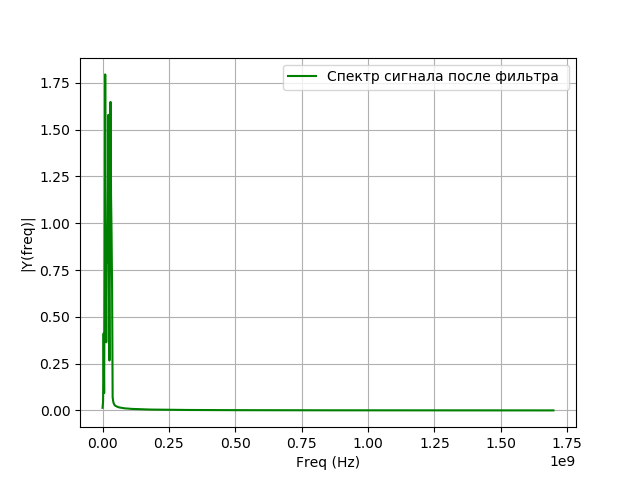
在上面的清单中,使用窗口方法实现了FIR带通滤波器的模型,选择了滤波器的阶数,以使滤波器的频率响应形状接近矩形。 模拟滤波器的系数数为n = 100001,即滤波器的阶数为P = 100000。
用于构造获得的FIR滤波器的频率响应和相位响应的程序:
我们得到:

FX相关器模型
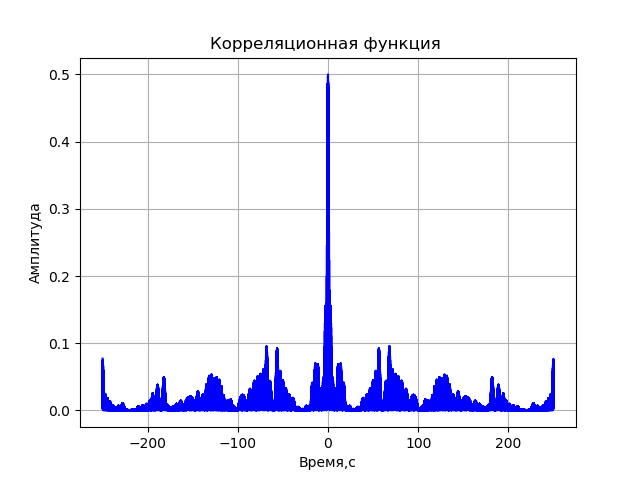
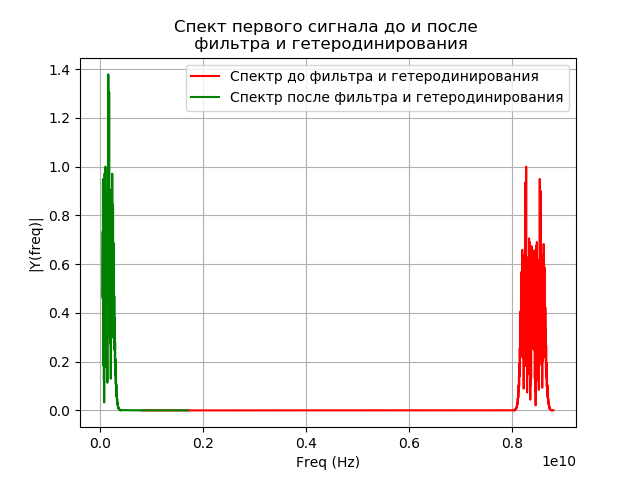
接下来,每个信号都经过快速傅立叶变换(FFT)。 使用scipy.fftpack中的fft库函数实现FFT。 得到的光谱是复共轭乘积:
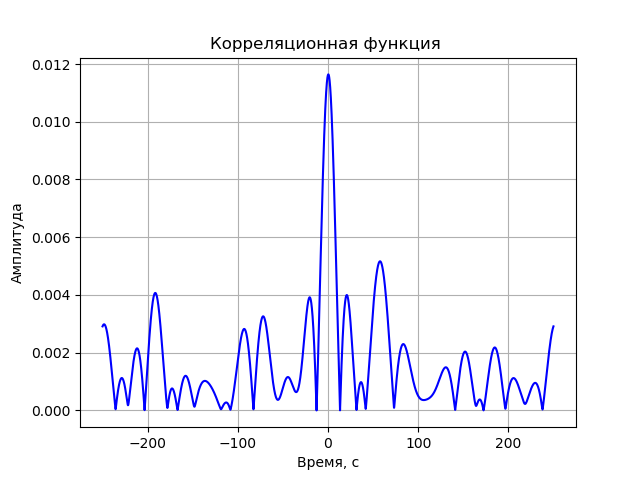
S(j omega)=S1(j omega)∗S2(j omega)=(a1+jb1)∗(a2−jb2)=a1a2+b1b2+j(b1a2−a1b2)最后一个动作是FFT的逆运算。 由于相关函数的幅度很重要,因此必须通过以下公式转换结果信号:
A= sqrtre2+im2用于关联函数的程序,不考虑注册系统的失真:
我们得到:
VLBI计算机模型的完整列表:
我们得到:

结论
- 简要介绍了射电天文学的发展历史。
- 分析了VLBI网络的当前状态。
- 考虑通过VLBI网络解决的问题。
- Python工具建立了具有二进制(两个位置)相位调制的导航信号模型-BPSK(二进制相移键)。 该模型使用相位调制的小波分析。
- 已经获得一种信号源模型,该信号源模型可以根据抑制旁瓣和中心瓣的最大幅度的标准来确定提供最佳相关函数的调制参数。
- 考虑到噪声和多普勒效应,获得了简化的VLBI网络模型。 考虑了使用具有有限脉冲响应的滤波器进行滤波的特征。
- 在简要介绍了理论之后,所有模型都配备了演示程序,可让您跟踪模型参数的影响。