手动分割肺部大约需要10分钟,并且需要一些技巧才能获得与自动分割相同的高质量结果。 自动分割大约需要15秒。
我假设没有神经网络,则可以获得不超过70%的精度。 我还建议形态学运算只是为更复杂的算法准备图像。 但是,由于处理了至少手头上的至少40个断层摄影样品,该算法选择了没有错误的肺部,并且在前五种情况下进行了测试之后,该算法并未发生重大变化,并且从第一次应用起,它就可以在其余35项研究中正确地工作而没有变化设置。
神经网络也有缺点-要进行训练,您需要数百个肺部训练样本,这些样本必须手动标记。
目录内容
呼吸系统的结构
呼吸系统包括气道和肺。 分配上呼吸道和下呼吸道。 下呼吸道和上呼吸道之间的分离点是食物和呼吸道的交点。 喉部上方的所有部分均在上部,其余部分则在下部。
我们列出了呼吸器官:
鼻腔 :-鼻子,上颌窦等
咽是食物和空气传播的通道。
喉 -负责声音形成。 位于颈椎C4-C6的水平。
气管 -连接喉和支气管的管。
支气管是呼吸道,其中大部分位于肺内。
肺是主要的呼吸器官。

洪斯菲尔德量表
戈弗雷·霍恩斯菲尔德(Godfrey Hounsfield)是一位英国电气工程师,他与美国理论家艾伦·科马克(Allan Cormack)共同开发了计算机断层扫描技术,并因此获得了1979年的诺贝尔奖。

霍恩斯菲尔德标度-以Hounsfield单位测量的定量X射线密度标度,用HU表示。
基于物质的衰减系数,即通过该物质时的辐射功率的降低程度,来计算X射线密度。
X射线密度通过以下公式计算:
$$显示$$ {μ_{X}-μ_{water} \超过μ_{water}-μ_{air}} \乘以1000 $$ display $$
在哪里 -被测物质,水和空气的线性衰减系数。
X射线密度为负,因为零X射线密度对应于水。 这意味着,与水相比,X射线波通过的所有物质的辐射功率减小的幅度要小于通过水的所有物质(例如,肺组织,空气)的负X射线密度。
以下是各种组织的近似X射线密度:
- 空气:-1000 HU。
- 呼吸器官:-950至-300 HU。
- 血液(无血管造影剂):0至100 HU。
- 骨骼:100至1000 HU。

维基百科链接: 霍恩斯菲尔德标度 , 戈弗雷·霍恩斯菲尔德 , 衰减系数 。
数学形态
本文选择的算法中的主要位置是形态运算。
在计算机视觉领域,形态学运算调用了一组用于变换对象形状的算法。 最常见的是,形态学运算应用于二值化图像,其中对象的体素对应于单位,而空白对应于零。
主要的形态学操作包括:
形态膨胀(膨胀,扩展) -将新体素添加到对象的所有边缘体素。 也就是说,沿着所有边界体素,使用具有给定形状(球,立方体,十字形等)的芯线进行通道。 此操作通常用于将许多相邻对象连接到单个对象中。
形态腐蚀(侵蚀,腐蚀) -破坏物体边界上所有体素的破坏。 此操作与扩张相反。 此操作对于消除许多相互连接的小物体形式的噪声很有用。 但是,仅当分割后的物体的厚度明显大于腐蚀半径时,才应使用这种噪声消除方法。
形态学闭合是扩张,随后是侵蚀。 它用于封闭对象内部的开口并合并相邻的对象。
形态上的开口(opening)是侵蚀,然后膨胀。 它用于去除小噪音物体并将物体分成几个物体。


Lee算法和RLE压缩
为了隔离二值化体素体积中的对象,使用了Lee算法。 该算法最初是为了找到最短路径而发明的。 但是,我们使用它来选择对象并将其从三维三维像素阵列移动到另一个三维像素阵列。 它的本质是从起点开始在所有可能的方向上平行移动。 对于三维情况,从给定体素移动26或6个方向是可能的(如果体素未位于图像边缘)。
为了优化速度,我们使用了行程编码算法。 它的本质在于以下事实:用与序列中元素数相等的数字替换一和零的序列。 例如,字符串“ 00110111”可以替换为:“ 2; 2; 1; 3”。 这减少了内存访问的次数。
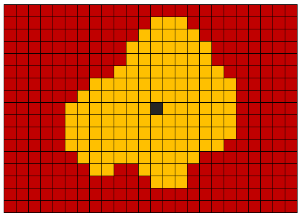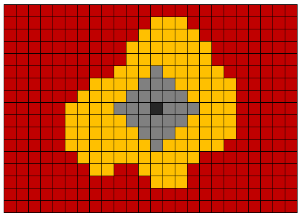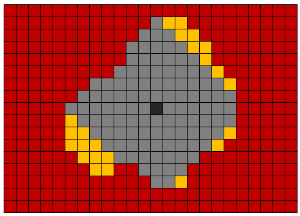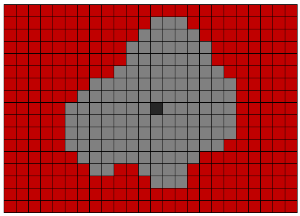

Wikipedia链接: Lee 算法,RLE算法 。
阈值基本音量转换
使用断层扫描仪,获得空间中每个点的X射线密度数据。 空气体素的X射线密度范围为-1100至-900 HU,呼吸器官体素的范围为-900至-300 HU。 因此,我们可以删除X射线密度大于-300 HU的所有多余体素。 结果,我们得到仅包含呼吸器官和空气的二值化体素体积。
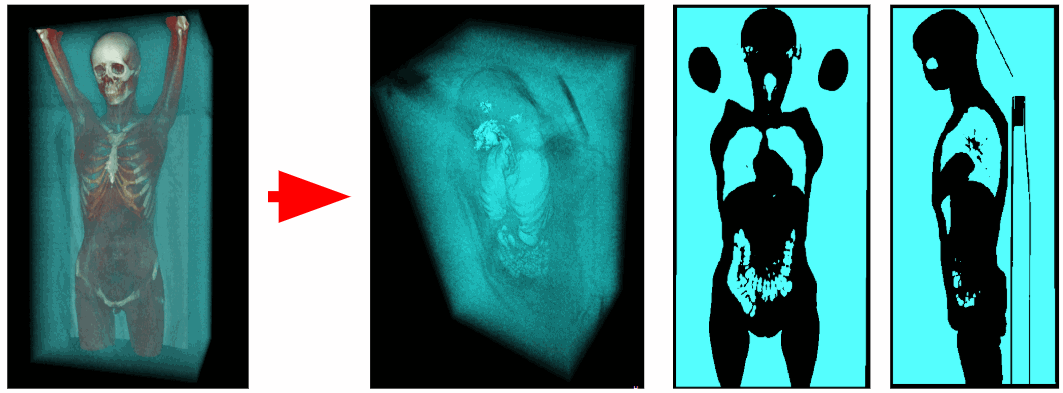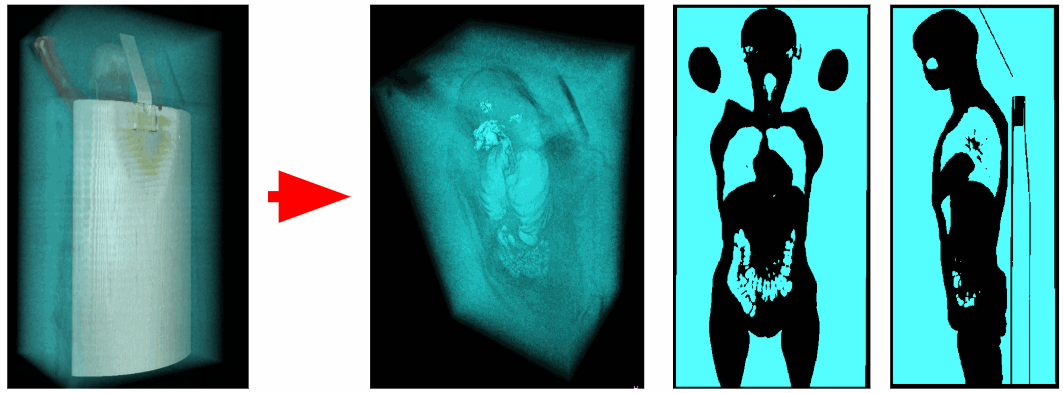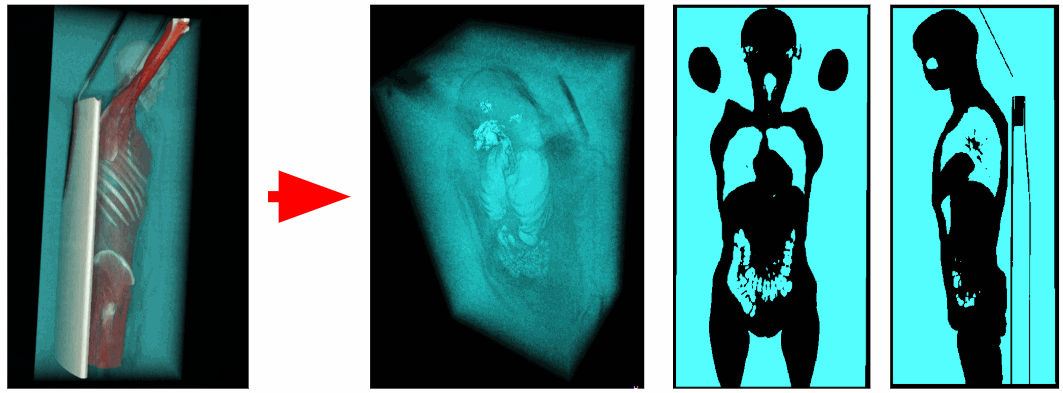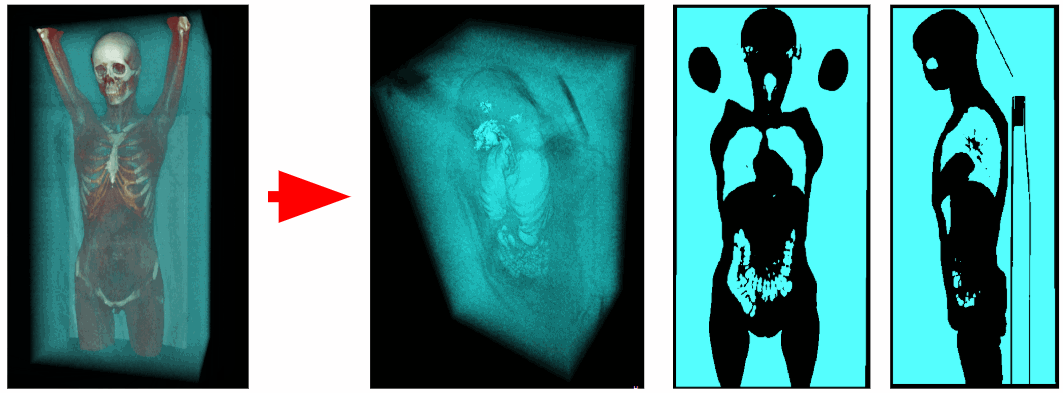
外部空气夹
为了隔离人体的内部空气,我们将移除所有靠近体素场景角落的对象。 这样我们就摆脱了外界的空气。

但是,并非所有情况都可以消除断层摄影台内的空气,因为它可能与场景的各个角落无关。

因此,我们将不仅扫描角落,而且扫描位于场景任何边界平面上的所有体素。 但是结果,由于某种原因,肺部本身也离开了。 事实证明,气管也与场景的上平面有关。
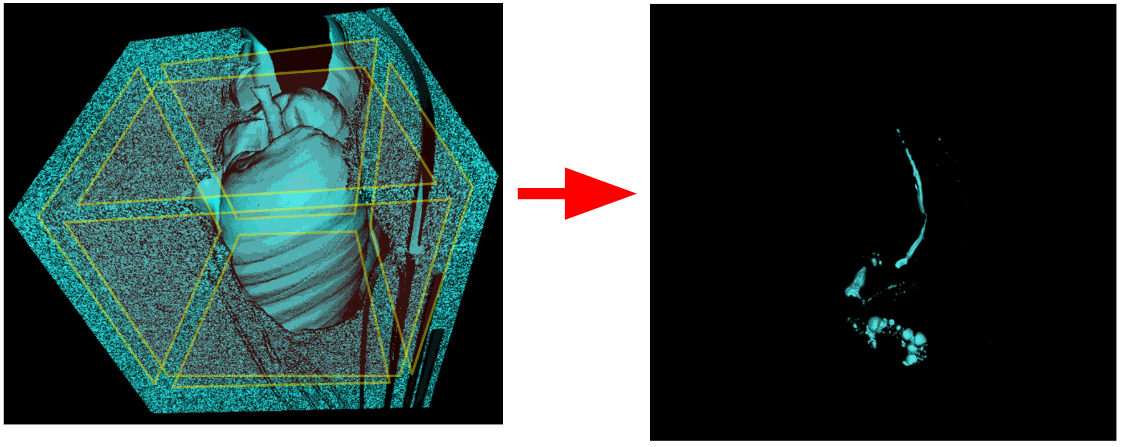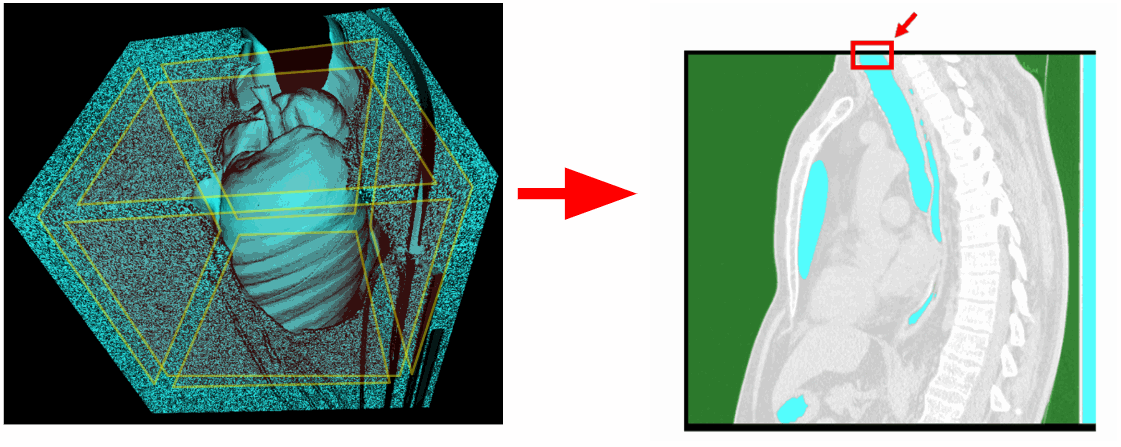
必须从扫描区域中排除上平面。 也有研究未完全捕获肺部并且下平面与肺部相关。 因此,如果需要,也可以排除下平面。

但是这种方法仅适用于乳房研究。 在捕获人体全部体积的情况下,通过鼻腔的内部和外部空气之间的连接将出现在图像上。 因此,有必要进行形态学侵蚀以分离内部和外部空气。
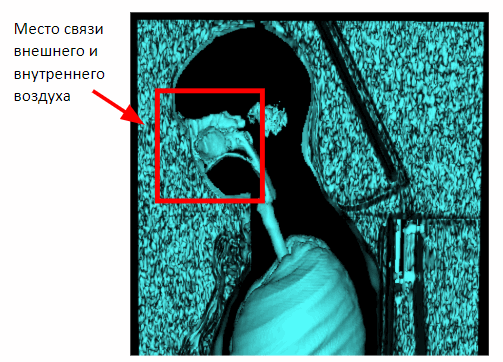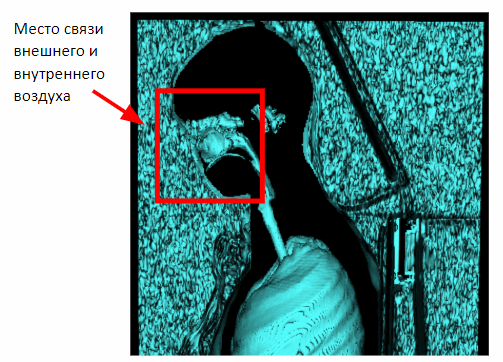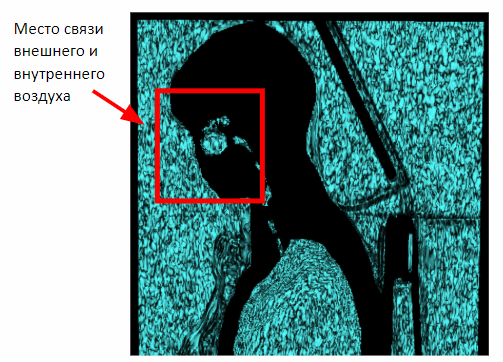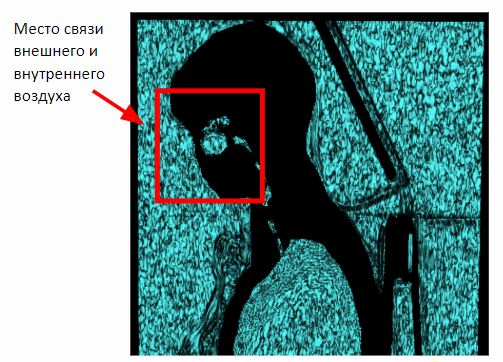
施加腐蚀之后,我们可以返回到先前获得的基于场景侧面的接近度来分割外部空气的方法。

通过隔离外部空气,人们可以立即将其从空气和肺的总体积中取出,并获得体内和肺部的内部空气。 但是有一个问题。 侵蚀后,有关外界空气的一些信息丢失了。 为了恢复它,我们应用了外部空气的膨胀。

接下来,我们从所有空气和呼吸器官中减去外部空气,得到内部空气和呼吸器官。


突出显示体积最大的对象
接下来,我们选择呼吸器官作为体积最大的对象。 呼吸器官是一个单独的对象。 肺与胃肠道内的空气之间没有任何联系。


值得注意的是,在阈值转换的初始步骤中正确选择X射线密度阈值很重要。 否则,在某些情况下,由于分辨率低,两个肺之间可能没有连接。 例如,如果您认为呼吸器官的体素的X射线密度为-500 HU或更小,则在以下情况下,由于两个肺之间没有连接,因此将呼吸器官分配为体积最大的对象将导致错误。 因此,阈值应增加到-300 HU。

肺内血管封闭
为了捕获肺内的血管,我们使用了形态学上的闭合,即扩张,然后以相同的半径进行侵蚀。 血管的X射线密度约为-100..100 HU。

大血管没有关闭。 但这不是必需的。 该手术的目的是破坏肺内的许多小孔,以利于进一步的肺分割。
呼吸分割算法
结果,我们获得了以下呼吸器官分割算法:
- 基本体积的阈值转换阈值<-300 HU。
- 半径为3毫米的形态腐蚀,用于分离内部和外部空气。
- 基于接近体素场景的边界侧面的外部空气分配。
- 外部空气的形态膨胀可恢复由于侵蚀而丢失的信息。
- 从所有空气和呼吸器官中减去外部空气以获得内部空气和呼吸器官。
- 突出显示最大体积的对象。
- 肺内血管的形态学闭合。

该算法在MATLAB中的实现
GetRespiratoryOrgans方法
GetExternalAir方法
GetMaxObject方法
源代码可以在这里下载。
结论
已计划以下文章:
- 气管和支气管的分割;
- 肺的分割;
- 肺叶分割。
算法例如:
- 距离变换
- 最近邻变换(最近邻变换,也称为特征变换);
- 计算Hessian矩阵的特征值以分割平面3D对象;
- 分割由分水岭分割。