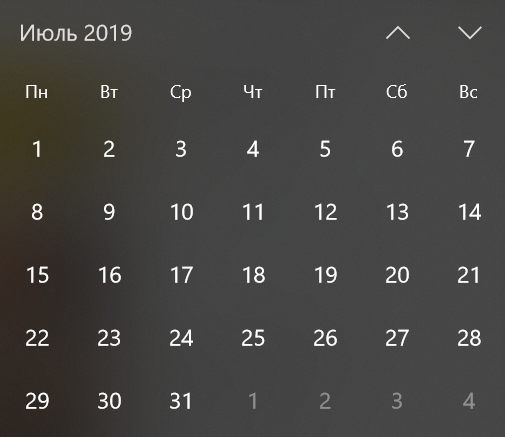
本文来自我昨天问自己的一个问题。
“是否有一年中没有一个星期一在星期一开始?”
乍一看,是的。 一年可以从一周中的任何一天开始,每个月也可以从一周中的不同日子开始。 有很多选择,最有可能的一年是这样。
所以我想了想之后的第一分钟。 应该证明这一点。 例如,经历多年。 一种简单快捷的方法,但并不有趣。 在数学上进行证明是一个更诱人的想法,但是我完全不知道如何解决这个问题。 因此,我才开始在纸上写出每个月的时间。
这里值得一提的是,我们将更多地讨论自1918年以来一直生活的
公历 。 但是,
朱利安(Julian)的推理是正确的。
实际上,这样的一年不存在。 让我们找出原因。
第1部分。
首先,请记住每个月有多少天:
现在,让我们看看每个月中有多少天超过四个星期。
此时,产生以下想法。 如果将日期添加7天,则星期几不会更改。 模块化算术工作。 从这里容易理解,如果一个月中的两天多于四周,那么相对于当月的第一天,下个月的第一天将偏移一周的两天。 反正
如果一个月中有(28 + N)天,则下个月的第一天将相对于当月第一天的星期几偏移N天。
例如,今年1月在星期二开始,因此2月在星期五开始。 周二+ 3 =周五
某月第一天的星期几? 要找到此信息,您需要汇总前几个月所有四个星期中的“剩余”天数。 该表显示了相对于1月1日星期几的变化。 第一行用于非-年,第二行用于a年。
但是,这看起来并不太明显,我们知道,轮班7天不会改变星期几。 因此,我们现在在表格中写入将总班次除以7后的残差。
现在另一件事! 如果知道1月1日的星期几,则可以清楚地看到如何确定每个月第一天的星期几。 您只需要为利息月份添加班次即可。 自高中起,我就知道2月-3月-11月的模式,但是我没有注意到其他模式。
在本文开头,我们得到了该问题的答案。
由于表中年份的两个版本都从0变为6,因此在任何一年中,都有一个月份从一周中的特定日期开始。
但是现在您可以提出其他问题了。 例如,“在哪个年份中只有一个这样的月份?” 或“在这些月份的哪几年中最多? 为此,您必须能够确定每年的1月1日的星期几。
第2部分。
当我学习编程的时候,这是在PascalABC学校的10年级时,首要的重要任务之一就是执行一个程序,该程序打印该年的日历,并以此作为论点。 我们对实现哪些功能有一些提示。 通常,归结为计算两个日期之间的天数:参考日期和当前日期,以确定所需年份的1月1日中的星期几。
这种方法有效,但是速度取决于所需年份与参考之间的接近程度。 这让我不高兴,但是我无法提出更好的选择。 现在,完全了解这一点的最佳时机已经到来。
公历中的年分配如下:
- 数是400的倍数的年份是a年
- 剩余的年份(非整数)是100的倍数
- 剩下的年份,是4的倍数,是leap年
- 剩下的几年是非飞跃的
此说明表明,跳跃周期的周期为400年。 但尚不清楚,这种四百年的周期是否会在一周的同一天开始。
请注意,每年的一月一日会每年偏移一周或两天,并写
一些代码。bool is_leap_year(int year) { if ((year % 400) == 0) return true; if ((year % 100) == 0) return false; if ((year % 4) == 0) return true; return false; } void first_weekdays_table() { ofstream file("weekdays.txt", ios_base::out); int weekday = 3; for (int i = 1801; i <= 3000; ++i) { file << weekday; if ((i % 100) != 0) { file << " "; } else { file << endl; } weekday += is_leap_year(i) ? 2 : 1; weekday %= 7; } file.close(); }
星期几显示在每年的1月1日,从1801年到3000年。星期一指定为“ 0”,星期二指定为“ 1”,依此类推。我们将以两个完整的四年周期和两个半周期的表格形式显示所有内容。 几个世纪以来,世纪都是垂直的。 在世纪和年份相交的单元格中,写下了今年开始的星期几。 例如,1997年开始的星期几在“ 1900”列和“ 97”行的交点处。 这是星期三。 该表的完整版本:
第1 部分 ,
第2部分 。


在表中,您会立即注意到两件事:四年周期实际上是在一周的同一天(2001、2401和2801;星期一)开始的,而不是2000,而是“千分之一”。 后者是有目的的,以提供更多便利。 第一个事实使我们能够继续前进,没有障碍。
在公历中,所有四百个周期都从星期一开始。
但是,最有趣的是表的完整版本。 您可能会发现,四百年周期中的每个世纪都包含一个重复的二十八年周期:
第一世纪以等于0的周期的移位开始,第二世纪以4的移位开始,第三以8的移位开始,第四以12的移位开始。为此,表格以存在一个世纪的``百分之一百''且不为零的形式表示。 值得一提的是,全年共有14种不同的选择。 在一个28年的周期中,每周的每一天一次,falls年的开始下降,而非-年的开始则是三倍。
现在我们可以确定任何日期的星期几,而无需使用参考日期。 为此,我们需要了解在一个四百年的周期中哪个世纪是一年,以及它在本世纪的情况是什么。 根据该表,我们可以确定一年中一月一日的星期几,并借助本文的第一部分-所需月份的特定日期的星期几。 而不是一千个字
我们将编写更多代码。 int get_weekday(int year, int month, int day) { int weekdays[] = {0, 1, 2, 3, 5, 6, 0, 1, 3, 4, 5, 6, 1, 2, 3, 4, 6, 0, 1, 2, 4, 5, 6, 0, 2, 3, 4, 5}; int shift_not_leap[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}; int shift_leap[] = {0, 3, 4, 0, 2, 5, 0, 3, 6, 1, 4, 6}; bool is_leap = is_leap_year(year); year -= 1; year %= 400; int century = year / 100; year %= 100; int index = (year + (4 * century)) % 28; int weekday = weekdays[index]; weekday += is_leap ? shift_leap[month - 1] : shift_not_leap[month - 1]; weekday += (day - 1); weekday %= 7; return weekday; }
从07/03/2019更新
如果您想象表格中有28年的周期,
0, 1, 2, 3, 5, 6, 0, 1, 3, 4, 5, 6, 1, 2, 3, 4, 6, 0, 1, 2, 4, 5, 6, 0, 2, 3, 4, 5
很明显,您如何计算星期几到1月1日的转变:
weekday = (index + (index / 4)) % 7;
鉴于此,以及well年的月份补偿可以通过非ap年的补偿来计算的事实,我们写道
下一个功能 int get_weekday_c(int year, int month, int day) { int shifts[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}; int shift = shifts[month - 1]; if (is_leap_year(year) and (month > 2)) { shift += 1; }; year = (year - 1) % 400; int century = year / 100; int index = ((4 * century) + (year % 100)) % 28; int weekday = (index + (index / 4)) + shift + (day - 1); return (weekday % 7); }
因此,您可以只知道12个数字就可以计算任何日期的星期几:星期几到每月第一天的偏移。
第3部分。总结
仅使用两个表,您可以确定任何日期的星期几,而无需使用参考日期。
在28年的周期中,1月1日是星期几的顺序:
非a年和leap年的工作日偏移量表,每个月的第一天:
在撰写本文时,我在Habré上发现了两个类似的主题:
一和
二 。 第一本书的作者使用一个特殊的表格,展示了如何在头脑中找到二十世纪和二十一世纪的日期。 他展示的表格包含56个数字。 本文中提出的算法使用星期几表和两个偏移表,其中包含(28 + 2 * 12)= 52个数字,您需要记住。 所有源代码都在
GitHub上 。
一个有趣的事实:从1918年2月1日到13日,在苏维埃俄罗斯没有一个人出生。
在星期天早上问自己问题=)