我们将继续讨论AISTATS 2019统计和机器学习会议。在这篇文章中,我们将分析关于树状集成的深层模型,高度稀疏数据的混合正则化以及交叉验证的高效时间近似的文章。

深林算法:基于不可分模块的非NN深度模型的探索
周志华(南京大学)
→ 演讲
→ 文章
实施-下面
来自中国的一位教授谈到了树木的合奏,作者称这是对不可微分模块的首次深度培训。 这似乎是一个太大声的声明,但是这位教授及其H-index 95受到邀请担任发言人,这一事实使我们可以更加认真地对待这一声明。 Deep Forest的基本理论已经发展了很长时间,原始文章已于2017年被引用(近200次引用),但是作者编写了库,并且每年他们都在提高算法速度。 现在看来,他们已经达到了最终可以将这一美丽理论付诸实践的地步。
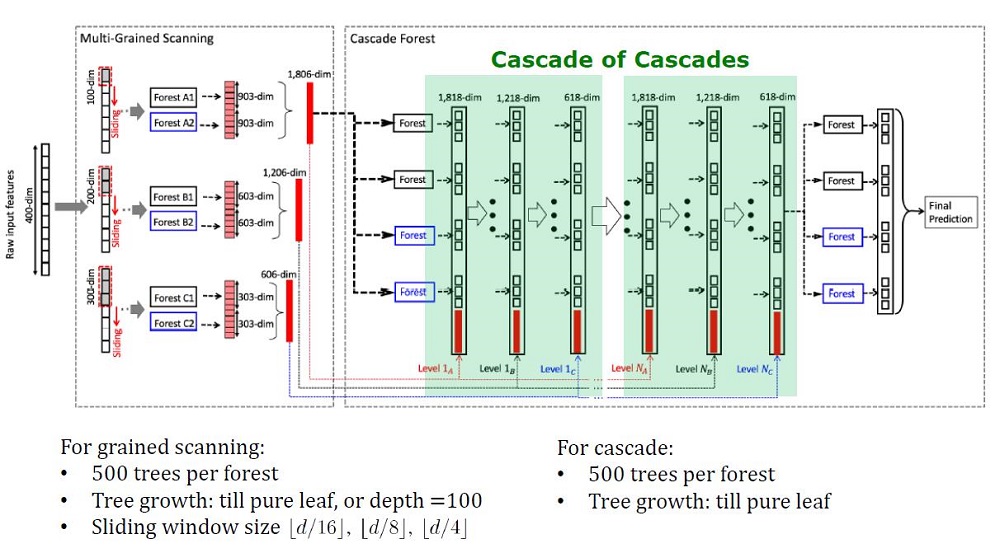
深林建筑概观
背景知识
深度模型(现在被称为深度神经网络)用于捕获复杂的数据依赖性。 而且,事实证明,增加层数比增加每层上的单元数更有效。 但是神经网络有其缺点:
- 不重新训练需要大量数据,
- 在合理的时间内学习需要大量的计算资源,
- 过多的超参数难以最佳配置
此外,深度神经网络的元素是可微分的模块,不一定对每个任务都有效。 尽管神经网络很复杂,但概念上简单的算法(例如随机森林)通常效果较好或较差。 但是对于此类算法,您需要手动设计功能,而这些功能也很难实现最佳化。
研究人员已经注意到Kaggle上的合奏:“非常完美”,并受到Scholl和Hinton的话启发,差异化是深度学习的最薄弱的一面,他们决定创建具有DL特性的树木合奏。
幻灯片“如何制作好合奏”
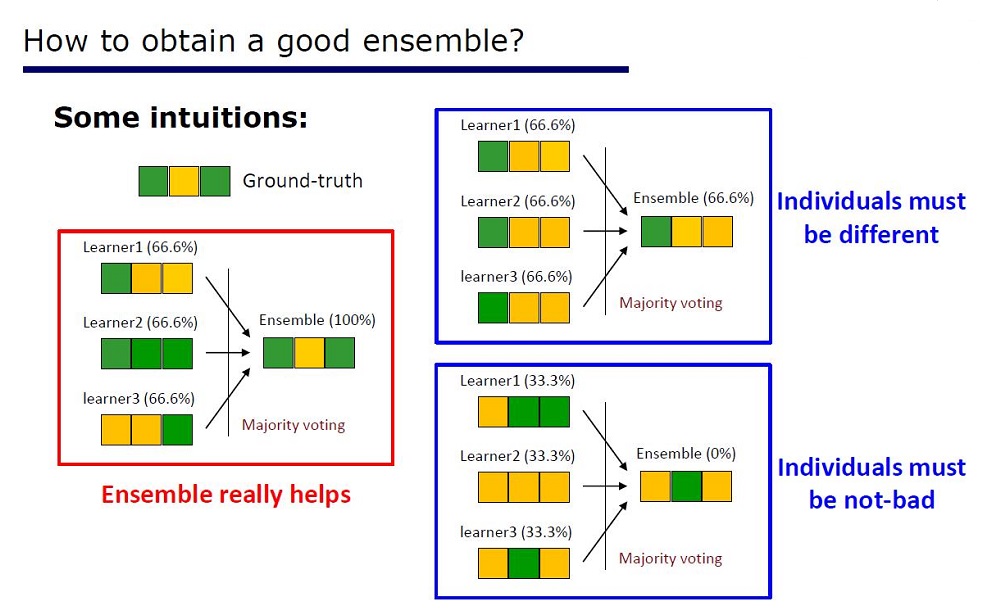
该架构是根据集合的属性推论得出的:集合的元素在质量上不应太差且有所不同。
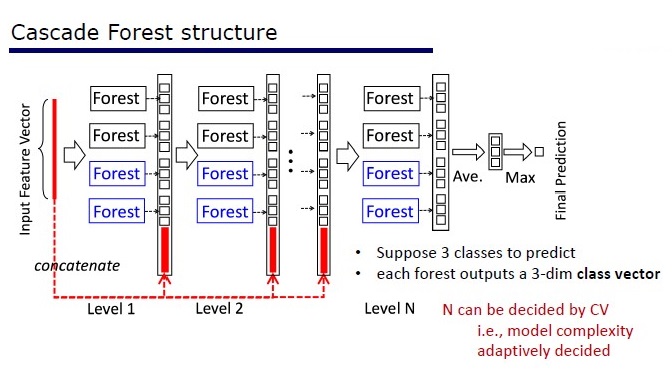
GcForest包含两个阶段:级联森林和多粒度扫描。 此外,为了避免级联的重新训练,它由2种树组成-其中一种是绝对随机树,可用于未分配的数据。 层数在交叉验证算法内部确定。
两种树
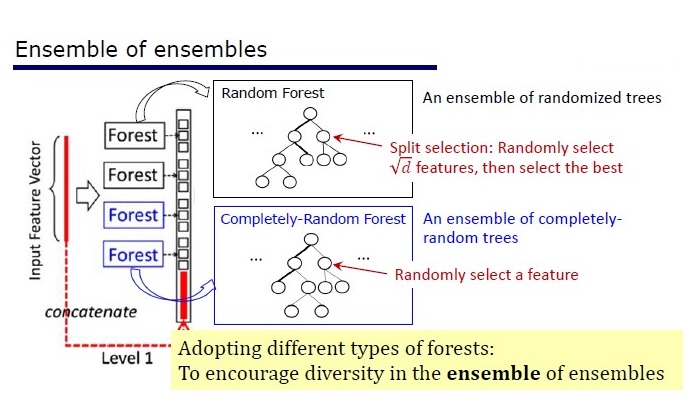
结果
除了标准数据集上的结果外,作者还尝试在中国支付系统的交易中使用gcForest来搜索欺诈行为,并使其F1和AUC远高于LR和DNN。 这些结果仅在演示中,但是在某些标准数据集上运行的代码在Git上。
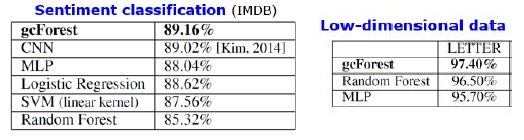
算法替换结果。 mdDF是gcForest的变体,是最佳的利润分配深林
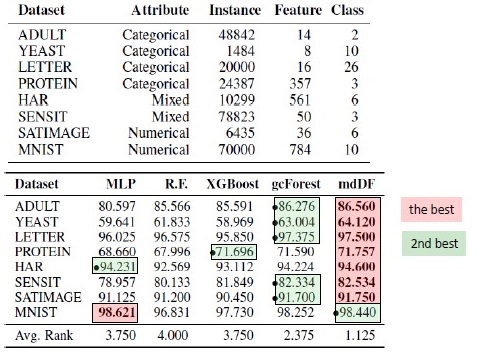
优点:
- 超参数很少,层数在算法内部自动调整
- 选择默认设置可以很好地完成许多任务。
- 模型的自适应复杂性,基于小数据-小模型
- 无需设置功能
- 它的工作质量与深度神经网络相当,有时甚至更好
缺点:
神经网络存在梯度衰减问题,而深林则存在“多样性消失”问题。 由于这是一个整体,因此使用的元素越“不同”和“好”,质量就越高。 问题在于作者已经尝试了几乎所有经典方法(采样,随机化)。 只要没有关于“差异”主题的新基础研究出现,就很难提高深林的质量。 但是现在可以提高计算速度。
结果的可重复性
XGBoost对表格数据很感兴趣,我想重现结果。 我获取了Adults数据集,并使用了文章作者的参数和默认参数的XGBoost来应用GcForestCS(GcForest的略微加速版本)。 在作者拥有的示例中,分类特征已经以某种方式进行了预处理,但是并未指出如何进行。 结果,我使用了CatBoostEncoder和另一个指标-ROC AUC。 结果在统计上有所不同-XGBoost获胜。 XGBoost的运行时间可以忽略不计,而gcForestCS的每次交叉验证有20分钟的5倍。 另一方面,作者在不同的数据集上测试了该算法,并将该数据集的参数调整为他们的特征预处理。
该代码可以在这里找到。
实作
→ 本文作者的官方代码
→经过官方改进的修改,速度更快,但是没有文档
→ 实施更简单
PcLasso:套索满足主成分回归
J. Kenneth Tay,Jerome Friedman,Robert Tibshirani(斯坦福大学)
→ 文章
→ 演讲
→ 使用例
2019年初,斯坦福大学的J.Kenneth Tay,Jerome Friedman和Robert Tibshirani提出了一种新的教学方法,该方法与老师一起,特别适合稀疏数据。
这篇文章的作者解决了分析基因表达研究数据的问题,这在Zeng&Breesy(2016)中进行了描述。 目标是p53基因的突变状态,可响应各种细胞应激信号来调节基因表达。 这项研究的目的是确定与p53突变状态相关的预测因子。 数据由50行组成,其中17行被归类为正常行,其余33行在p53基因中携带突变。 根据Subramanian等人的分析。 (2005)308个在15和500之间的基因集在此分析中。 这些基因试剂盒总共包含4,301个基因,可在grpregOverlap R软件包中获得。 扩展数据以处理重叠的组时,将输出13,237列。 本文的作者使用了pcLasso方法,这有助于改善模型结果。
在图片中,使用“ pcLasso”时,AUC有所增加

方法的本质
方法结合  -正规化与
-正规化与  ,从而将系数向量缩小到特征矩阵的主要成分。 他们称所提议的方法为“核心套索组件”(R上有“ pcLasso”)。 如果变量已预先分组(用户选择要分组的内容和方式),则该方法特别强大。 在这种情况下,pcLasso压缩每个组并沿该组主要组件的方向获取解决方案。 在求解过程中,还将对可用组中的重要组进行选择。
,从而将系数向量缩小到特征矩阵的主要成分。 他们称所提议的方法为“核心套索组件”(R上有“ pcLasso”)。 如果变量已预先分组(用户选择要分组的内容和方式),则该方法特别强大。 在这种情况下,pcLasso压缩每个组并沿该组主要组件的方向获取解决方案。 在求解过程中,还将对可用组中的重要组进行选择。
我们提出了特征中心矩阵奇异分解的对角矩阵  如下:
如下:
我们将中心矩阵X(SVD)的奇异分解表示为  在哪里
在哪里  是由奇异值组成的对角矩阵。 以这种形式
是由奇异值组成的对角矩阵。 以这种形式  -正则化可以表示为:
-正则化可以表示为:
 在哪里
在哪里  -对角矩阵,包含奇异值平方的函数:
-对角矩阵,包含奇异值平方的函数: %2C%E2%80%A6%2CZ_%7B22%7D%3Df_2%20(d_1%5E2%2Cd_2%5E2%2C%E2%80%A6%2Cd_m%5E2%20)) 。
。
一般而言,  -正规化
-正规化  对于所有
对于所有  对应
对应  。 他们建议最小化以下功能:
。 他们建议最小化以下功能:
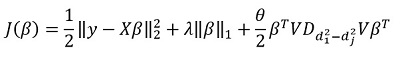
在这里  -对角元素差异矩阵
-对角元素差异矩阵  。 换句话说,我们控制向量
。 换句话说,我们控制向量  也使用超参数
也使用超参数  。
。
转换此表达式,我们得到解决方案:
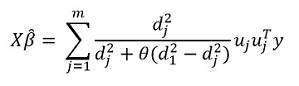
但是,该方法的主要“功能”当然是对数据进行分组的能力,并且可以在这些分组的基础上突出显示该分组的主要组成部分。 然后,我们以以下形式重写解决方案:
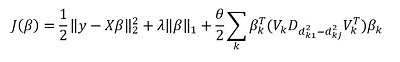
在这里  -矢量子向量
-矢量子向量  对应于组k
对应于组k ) -奇异值
-奇异值  降序排列
降序排列  -对角矩阵
-对角矩阵 
有关目标功能的解决方案的一些注意事项:
目标函数是凸的,非平滑分量是可分离的。 因此,可以使用梯度下降有效地优化它。
方法是提交多个值  (包括零,分别获得标准
(包括零,分别获得标准  -regularization),然后进行优化:
-regularization),然后进行优化:  接
接  。 因此,参数
。 因此,参数  和
和  选择进行交叉验证。
选择进行交叉验证。
参量  很难解释。 在软件(pcLasso软件包)中,用户设置此参数的值,该值属于间隔[0,1],其中1对应于
很难解释。 在软件(pcLasso软件包)中,用户设置此参数的值,该值属于间隔[0,1],其中1对应于  = 0(套索)。
= 0(套索)。
实际上,改变值  = 0.25、0.5、0.75、0.9、0.95和1,则可以涵盖各种模型。
= 0.25、0.5、0.75、0.9、0.95和1,则可以涵盖各种模型。
算法本身如下

该算法已经用R编写,如果您愿意,您可以使用它。 该库称为“ pcLasso”。
瑞士军用极小折刀
Ryan Giordano(加州大学伯克利分校); 威廉·斯蒂芬森(麻省理工学院); 刘润京(加州大学伯克利分校);
迈克尔·乔丹(加州大学伯克利分校); 塔玛拉·布罗德里克(麻省理工学院)
→ 文章
→ 代码
机器学习算法的质量通常通过多次交叉验证(交叉验证或引导)来衡量。 这些方法功能强大,但在大型数据集上速度较慢。
在这项工作中,同事使用权重的线性近似,得出的结果工作更快。 这种线性近似在统计文献中被称为“无穷大折刀”。 它主要用作证明渐近结果的理论工具。 无论权重和数据是随机的还是确定性的,本文的结果均适用。 结果,该近似顺序地估计了任何固定k的真实交叉验证。
向作者颁发论文奖

方法的本质
考虑估计未知参数的问题  在哪里
在哪里  紧凑,我们的数据集的大小是
紧凑,我们的数据集的大小是  。 我们的分析将在固定的数据集上进行。 定义我们的评级
。 我们的分析将在固定的数据集上进行。 定义我们的评级  如下:
如下:
- 对于每个
 设置
设置  (
(  )是
)是 
 是一个实数,并且
是一个实数,并且  是一个向量,由
是一个向量,由 
然后  可以表示为:
可以表示为:

通过梯度方法解决此优化问题,我们假设函数是可微的,并且可以计算出Hessian。 我们解决的主要问题是与评估相关的计算成本 ) 对于所有
对于所有  。 作者的主要贡献是计算
。 作者的主要贡献是计算 ) 在哪里
在哪里 ) 。 换句话说,我们的优化将仅取决于导数
。 换句话说,我们的优化将仅取决于导数 ) 我们假设存在并且是黑森州:
我们假设存在并且是黑森州:
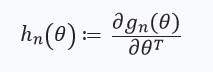
接下来,我们定义一个带有固定点及其导数的方程:
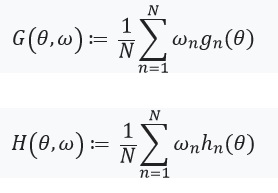
这里值得关注的是 %2Cw)%3D0) 从
从 ) -解决方案
-解决方案 %3D0) 。 我们还定义:
。 我们还定义: ) ,权重矩阵为:
,权重矩阵为:  。 在这种情况下
。 在这种情况下  有一个逆矩阵,我们可以使用隐函数定理和“链式规则”:
有一个逆矩阵,我们可以使用隐函数定理和“链式规则”:
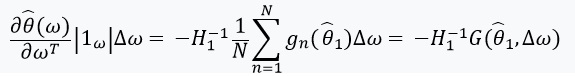
该导数使我们能够形成线性近似 ) 通过
通过  看起来像这样:
看起来像这样:
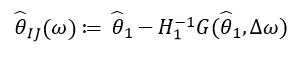
由于  仅取决于
仅取决于  和
和  ,而不是来自其他任何值的解决方案
,而不是来自其他任何值的解决方案  因此,无需重新计算并找到新的ω值。 相反,需要求解SLE(线性方程组)。
因此,无需重新计算并找到新的ω值。 相反,需要求解SLE(线性方程组)。
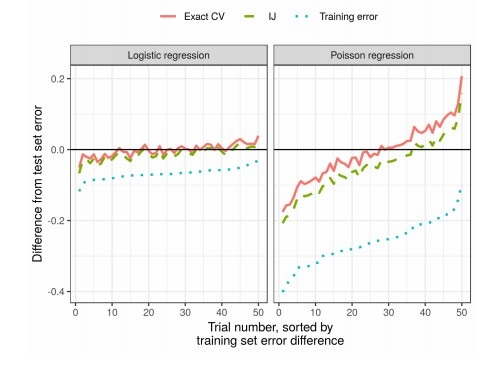
结果
实际上,与交叉验证相比,这大大减少了时间: