“存在经济的唯一原因是激发数学家新的探索。”
2013年，Alexey Savvateev就社交网络和互联网的模型进行了多次演讲。 我发现这个话题很好奇，不应该被忘记。 让我们尝试了解这个问题。 我也很想知道此后的情况如何变化，以及该领域有哪些有用的出版物。
无论是在Internet上还是在社交网络的生物学中，它们都表现出模型分别描述的属性，但这些属性却合在一起-混淆了现代数学。 Savvateev声称“处理这一问题的人将获得诺贝尔奖”。 未来将取决于与网络合作的能力。
以下是对三个演讲视频的汇总整理，视频本身位于结尾。
（该帖子看起来像一组带有讲师引号的幻灯片，要将所有内容绑定到一个简洁的文本中，我缺乏俄语和数学技能，但是该主题非常重要，因此我想将其发布。）社交网络包括：
连接可以是双向的（朋友，共同作者），也可以是单向的（订户）。 社会总是存在的，但是只有随着在线网络的出现，才有可能在宏观层面上研究它们。 过去十年来，人类取得了巨大的飞跃。 它学会了从整体上审视自己。 它可以数字化。 收集有关您自己的信息。
当指示“粘结强度”的系数时，建立加权图模型将是公平的。 但是对我们来说，就像对月亮一样。
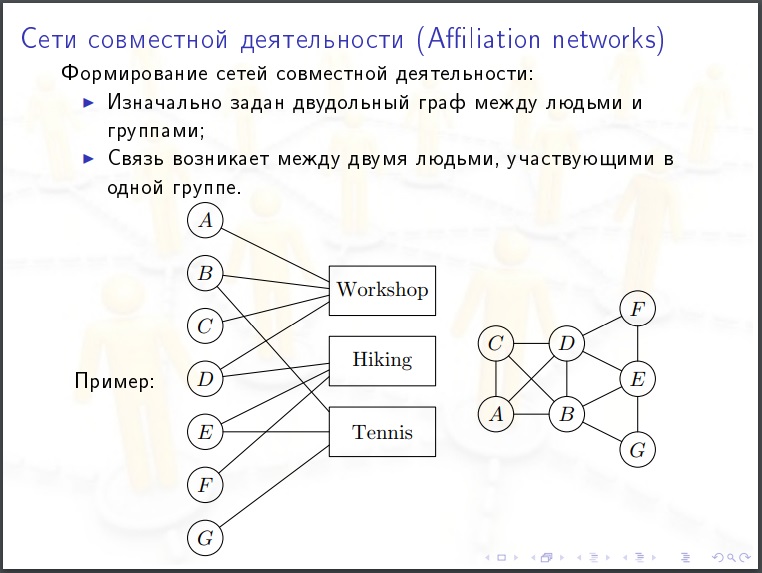
艺廊
看照片很有用。 观看图片后您可能提出的假设显然是荒谬的。
谁对学习社交网络有用
经济学：假设
经济中的微观和宏观水平是通过“网络”联系在一起的
政治学：人们会假设政权是否会保留还是会改变，这取决于谁将拥有更强大的网络专家。
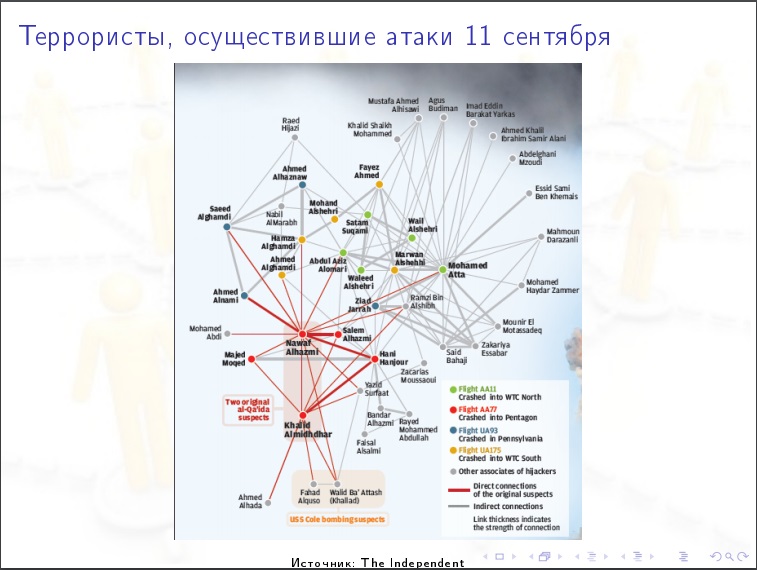社交媒体分析示例。社交网络的数值特征
- 距离
- 内径
- 顶点度
- 顶点度分布
- 节点中心度度量
- 中心分布
- 聚类系数
- 分类系数
距离 -从一个顶点到另一个顶点需要传递多少条边。
直径是图中的最大距离。
顶点的度数是顶点处的边数。
六次握手论
任何社交图的平均直径都非常低（
“六次握手理论” ）。 而且，有一个非常密集的核心。 我通过我的总统与一些非洲人“熟悉”，这些总统与非洲总统握手。
局部聚类系数 。 我们看一个人的所有邻居，“ k”个片断。 最大肋骨-k（k-1）/ 2。 我们查看实际的边数，然后除以该最大值。
全局聚类因子 。 与“复选标记”相比，有多少个“三角形”。
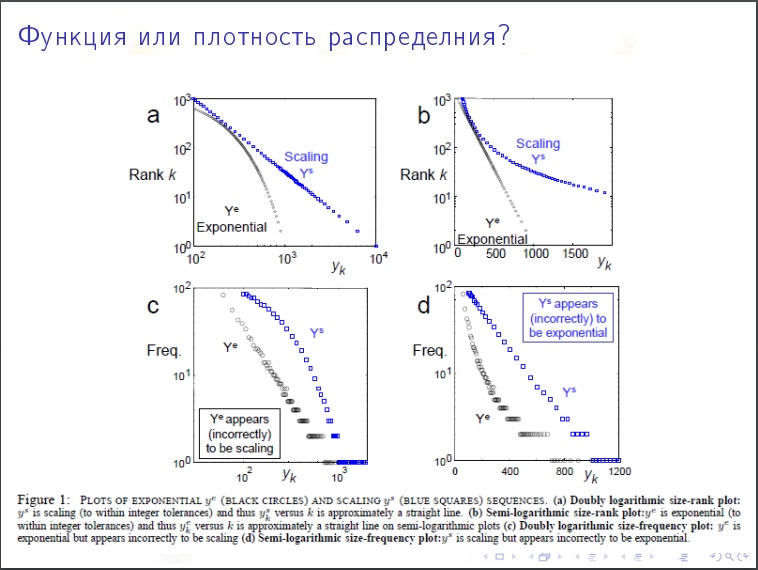
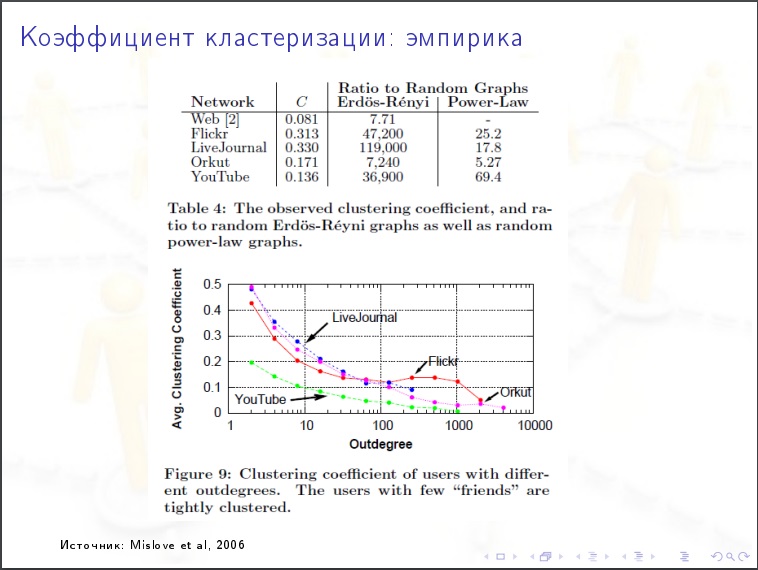顶点的度分布 。 度小于1000的顶点占百分之几？ 分布的性质是指数还是指数？ 事实证明，互联网具有固定的性质。
系数为“ 2”。 度为“ x”的顶点将为N / x
2 。 我们检查在LJ中有十亿用户，千分之千应除以千到千平方。 千分之一。
这是一件非常缓慢的事情。
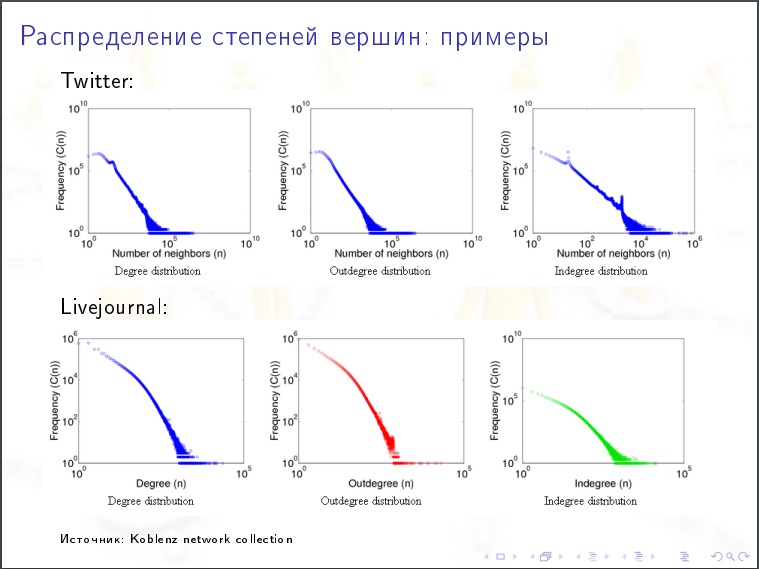
分类系数 。 粗略的方法-我们以几乎相同的度数来获取峰，它们相互连接的可能性更大还是更少？ 如果是这样，则将其分类。 分散性-次数较多时，可能性较小。 这是一种幼稚的方法。 这是一种更正确的方法。 在每个顶点处都有一些其他特征（银行的总资本），该指标看起来具有可分类性。
社交网络
节点的中心性 。 我们采取一个人，我们认为对他来说以下价值。 我们对所有其他人对（N-1）（N-2）/ 2进行排序，并且在每种情况下，我们都询问图中最接近的约会路径，它是否经过此人？ 可能有最短的路径，其中一些包含我们的人，然后我们给他％。 这是社交网络中最重要的特征。 对于流行病的传播，公众舆论。 这是需要衡量的。
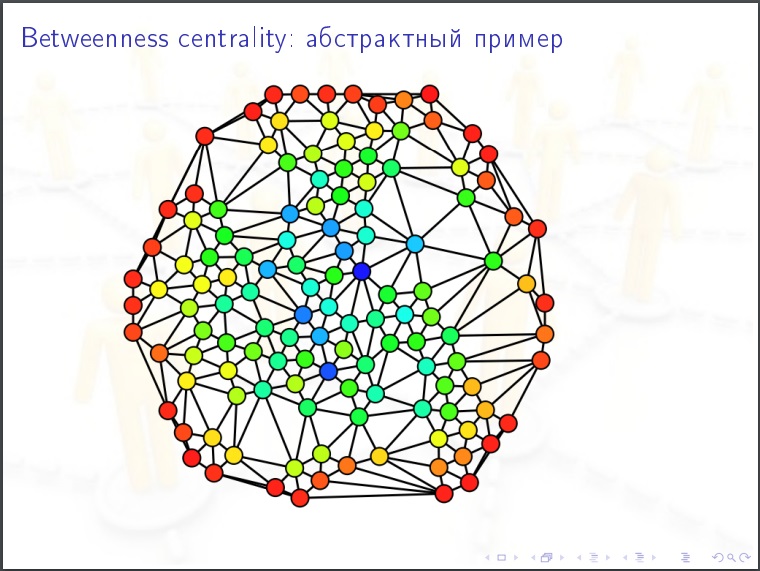
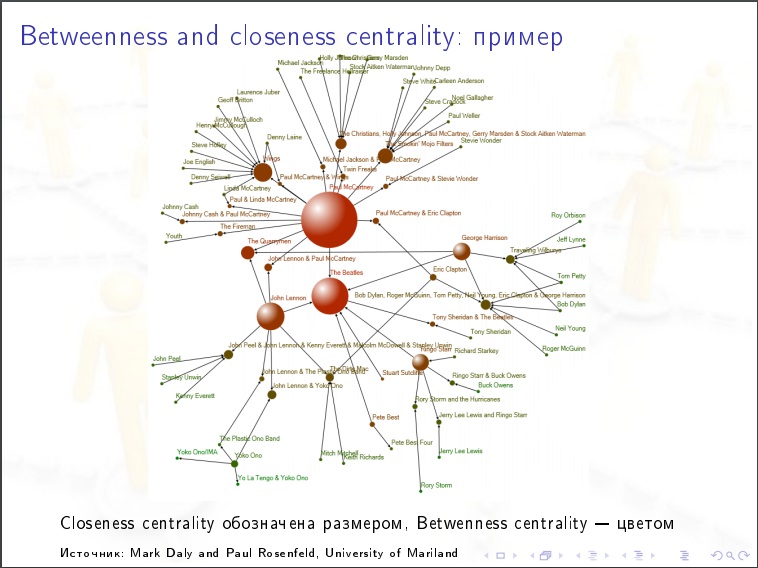
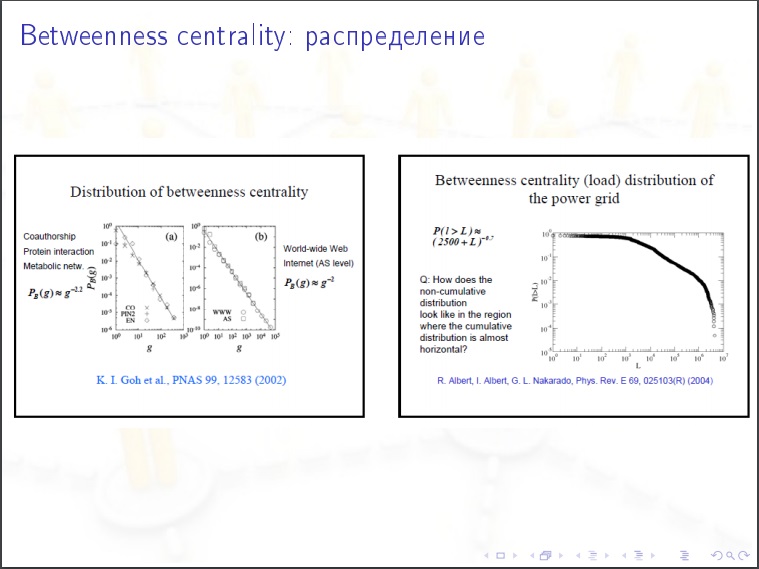
社交网络的特点：- 小直径和顶点之间的平均距离
- 顶点度分布和中间性中心的幂定律
- 高聚集率
- 分类
- 存在密切相关的核心
任务是创建一个覆盖前三个属性（最好是后两个属性）的模型。 目前，前三个已经是无法克服的复杂性。 对于2013年，没有这样的模型。
我们转向对已存在的随机图模型的描述。
型号
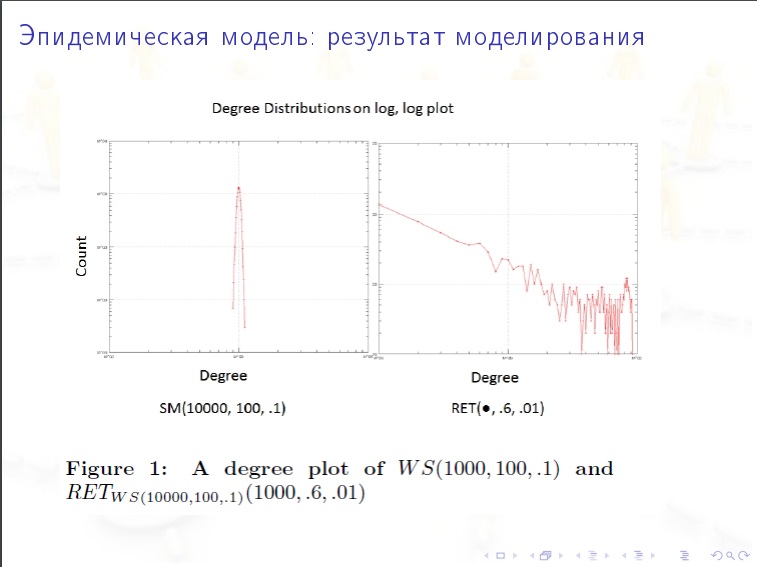
型号有：- 技术性（边缘随机产生）
- 博弈论（对某人有利时）
- 没有结构（只有很多顶点）
- 结构性的（顶点是度量空间的点或具有权重；一组顶点上有一个结构）
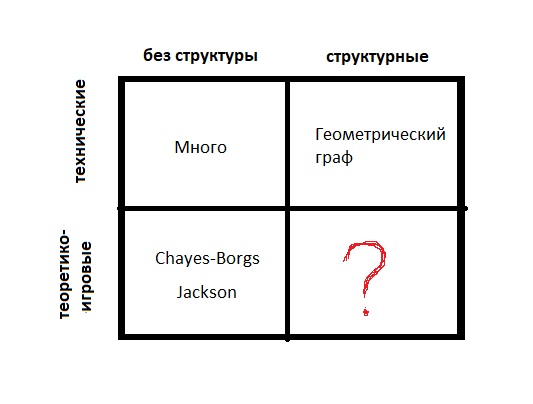
如果您了解基本原理，则可以使用大量参数作为指导。 如果精心选择的参数给出了很好的近似值，那么您做得很好。 即使最佳组合给出了不好的结果并且与观察到的事实不一致，也告别。
所有这一切都是出于一个目的-与垃圾邮件作斗争。
可以将Internet想象成一个复杂的网络，其层次如下：
- 技术水平 。 顶点和边是节点和通讯线。
- 超文本级别 。 顶点是站点或页面，边缘是超链接。
- 社会层面 。 顶点是用户，边是它们之间的那些或其他连接：社交网络上的友谊，博客的订阅，分布式项目中的协作（例如Wikipedia）等。
对于复杂的网络，许多本地和全局数值特征是已知的：顶点度的分布，聚类系数，分类系数
事实证明，Internet网络具有许多功能：
对Internet网络进行建模的最终目标是建立具有相同功能的模型。
鄂尔多斯模型-仁义
鄂尔多斯-仁义模型是两个紧密相关的随机图生成模型之一。 这些模型以数学家PalErdös和Alfred Renyi的名字命名，他们是1959年首次引入其中一种模型的。 探索了约会图。
考虑N点。 潜在边缘-N *（N-1）/ 2。 对于每个肋骨，我们进行随机测试。 肋骨发生的可能性-p。 没有发生什么-（1-p）。 让我们运行“测试”，得到一个图形。 但是有一些问题。 为了显示“稀疏”属性，
p必须非常小，约为1 / N，然后直径会非常大。
任何听到根据Erds-Renyi模型将互联网描述为随机图的研究人员都会大笑。
一个有趣的效果是，当您克服某个概率阈值时，该图将变为连接。
Bollobashi模型
这是用于构建Internet的动态模型。 我们正在尝试猜测它是如何逐渐形成的。 这个想法是这样的。 我们绘制一个具有一个顶点和一个边缘的图形，然后在每一步中我们随机进行游戏。 我们添加一个顶点，之后，它以一定概率关闭自身，并以一定概率连接到前一个顶点。 下一个可能会关闭的峰会自行关闭，有些会接近前一个峰。 而且，到达顶部的概率总是与边缘的数量成正比。 将播放一个随机值，下一个抽奖取决于前一个的结果。 这样的模型是直观的，但是在数学上很难计算。 该模型给出了非指数的功率分布。 直径是相同的。
但是此模型不适用于群集。
有两种相互竞争的方法可用于群集。
几何方法
该假设来自最高限额。 Internet图基于度量空间。 品味，兴趣，喜好的空间。 人们彼此之间有多有趣。 看来，精神上有多亲密。 如果人们很亲密，他们会互相指责。
我们将10
10分扔进这个空间。 大量参数出现在这里。 巨大的
聚类非常好，但是递减的顶点是指数的。 争议。
这种方法非常简单，算法是“偶然”完成的。
游戏博格博弈论方法
您是否知道在冯·诺伊曼（von Neumann）时代宣布博弈论将成为对抗苏联的新一代武器？我们假设人们做出决定是否相互交流。
我们组织会议/活动。 活动是受邀嘉宾及其“强度”的列表。
费用=强度*（常数+ K *（被邀请人数））。 我必须花费资源来“出售”该事件，并且我必须在每个参与者上花费更多。 有生日，有远足。 出现“ P”系数，该系数对于生日而言较小，对于远足而言较大。 强度约会。
一个人可以组织多个强度为P
1 ，P
2 ... P
n的事件 。 其他人也一样。
我有建立社会联系的行动，也有陌生人。
获胜函数=（您熟悉的人数）-费用
“足够熟悉”表示您在一起的所有事件的强度总和大于某个阈值。 谁组织了活动都没有关系。
排骨是为了结识足够的人。
证明了在该模型中获得了实际闭合的许多特性。 在所有纳什均衡中，还观察到了实际的封闭特性甚至更强的聚类特性，这在真实Internet的图表中也可以观察到。
但是其他属性尚不清楚，但这是麻烦的一半。 问题在于，如果至少有两个人彼此认识的至少一个纳什均衡，那么就有一个每个人都熟悉的纳什均衡。
有一种将两种方法结合起来的想法。 考虑到人们生活在度量空间中，当他们组织事件或参加事件时，成本，强度和阈值比率取决于“接近度”。 这是第五代模型。
差异化成本
选择权是使差异成本和差异胜利。 有些比其他的更容易被邀请。 与一个人相识比与另一个人相识更有利可图。
假设我们将所有人均匀地分布在周围。 邀请更亲密的人更便宜。 余额会是什么样？ 每个人都会邀请一些邻居，对吗？ 不对 没有这种平衡。
证明。 假设它存在，那么已经邀请了彼此接近的人们参加许多不同的会议。 然后，他不需要邀请这个亲人。 该平衡的存在与该平衡的存在相矛盾。
发现存在纯平衡，这是唯一的平衡。 每个对象都邀请一个邻域，该邻域位于（或逆时针）一定距离和一定距离处。
（-这是星系的形成！）
（-这是自发的对称破坏！）结论
佩列文曾经写道：“俄罗斯人的生活意义在于对巨大圣像的轻装上阵。” 这就是数学的含义-同样。 只有圣障是科学的。
这是一个高度多学科的研究。 您可以想象的更高。
资料来源
聚苯乙烯
“一旦我被邀请去纳瓦尼俱乐部，就会有一些年轻人，狂热者帮助他。 我立即警告我说些不愉快的话。 如果支持革命的数学家比反对的数学家更强大，那么革命就是胜利。 Navalny的年轻人不知道如何告诉他们这样的模型，但是他们不了解，他们甚至不知道如何整合-他们只是在某个地方大喊大叫。 面对他们的是一个强大的研究所，最重要的是负责人。根据克里姆林宫的命令，这些人说谁应该被捕，应该逮捕多少人，以便什么也没有。 他们说：“我们权力下放-特别是纳瓦尔尼并不代表任何东西，有几个重要的领导人。” 然后，一个数学家来了，并相信集中化是该网络的90％。 您封锁了您需要的某人几天-而没有革命。 数学胜出。”
-Alexey Savvateev， “革命要有好的数学家才能赢得胜利”
PPS
谁知道社交网络领域还有哪些有趣的作品（文章，讲座）及其实际收益，请分享。