神经网络和深度学习，第3章，第1部分：改进神经网络的训练方式

当一个人学习打高尔夫球时，他通常会花费大部分时间进行基本击球。 然后，他根据基本的打击逐渐发展出其他打击，并研究这些技巧。 同样，到目前为止，我们一直专注于了解反向传播算法。 这是我们的“基本罢工”，是使用神经网络（NS）进行大多数工作培训的基础。 在本章中，我将讨论一组可用于改进反向传播的更简单实现以及改进NS教学方法的技术。

我们将在本章中学习的技术包括：成本函数作用的最佳选择，即具有交叉熵的成本函数； 四个所谓 正则化方法（L1和L2的正则化，神经元的排除[辍学]，训练数据的人工扩展），可提高我们NS在训练数据之外的通用性； 初始化网络权重的最佳方法； 一组启发式方法，可帮助您为网络选择良好的超参数。 我还将在表面上考虑其他几种技术。 在大多数情况下，这些讨论是相互独立的，因此您可以根据需要跳过它们。 我们还在工作代码中实现了许多技术，并使用它们来改进为手写数字分类任务所获得的结果，这在第1章中进行了研究。

当然，我们只考虑为神经网络开发的大量技术中的一小部分。 最重要的是，进入大量可用技术领域的最佳方法是详细研究一些最重要的技术。 掌握这些重要的技术本身不仅有用，而且还将加深您对使用神经网络时可能出现的问题的理解。 因此，您将准备根据需要快速适应新技术。

交叉熵成本函数

我们大多数人都不喜欢错。 开始学习钢琴后不久，我在观众面前举行了一场小型音乐会。 我很紧张，开始演奏比需要低八度的乐曲。 我很困惑，直到有人向我指出一个错误，我才能继续。 我很as愧。 但是，尽管这很不愉快，但我们还是很快就学到了，认为我们错了。 当然，下次我与观众交谈时，我会以正确的八度演奏！ 相反，如果我们的错误定义不明确，我们的学习速度就会变慢。

理想情况下，我们希望神经网络能够从错误中快速学习。 在实践中会发生这种情况吗？ 为了回答这个问题，让我们看一个牵强的例子。 它涉及一个只有一个输入的神经元：



我们正在教这个神经元做一件非常简单的事情：接受1并给0。当然，我们可以通过手动选择权重和偏移量而无需使用训练算法，来找到这样一个琐碎问题的解决方案。 然而，尝试使用梯度下降来获得重量和位移是非常有用的。 让我们看看神经元是如何训练的。

为了确定性，我将选择0.6的初始权重和0.9的初始偏移量。 这些是分配给起点的一些常规值，我没有特别选择它们。 最初，输出神经元产生0.82，因此我们需要学习很多知识才能接近期望的输出0.0。 原始文章具有一个交互式表单，您可以在该表单上单击“运行”并观察学习过程。 该动画没有预先录制，浏览器实际上是计算渐变，然后使用它来更新权重和偏移并显示结果。 学习速度为η= 0.15，足够慢，可以看到正在发生的事情，但足够快，可以在几秒钟内完成学习。 在第一章中介绍了成本函数C是二次方的。 我会很快提醒您其确切的形式，因此没有必要再来这里找回。 只需单击“运行”按钮，即可多次开始训练。

如您所见，神经元快速学习了权重和偏见，从而降低了成本，并提供了0.09的输出。 这不是0.0的理想结果，但是很好。 假设我们选择初始权重和偏移量为2.0。 在这种情况下，初始输出将为0.98，这是完全错误的。 让我们看看在这种情况下神经元将如何学习产生0。

尽管此示例使用相同的学习率（η= 0.15），但我们看到学习速度较慢。 在最初的大约150个时期，重量和位移几乎不变。 然后训练加速，几乎和第一个示例一样，神经元迅速移动到0.0。 这种行为很奇怪，不喜欢学习一个人。 正如我在开始时所说的，当我们非常错误时，我们经常会学习得最快。 但是，我们只是看到了人造神经元如何非常困难地学习，犯了很多错误-比他犯了一点错误时要困难得多。 而且，事实证明，这种行为不仅在我们的简单示例中出现，而且在更通用的NS中出现。 为什么学习这么慢？ 我可以找到避免这种问题的方法吗？

为了理解问题的根源，我们记得我们的神经元通过重量和位移的变化来学习，其速率由成本函数theC /∂w和∂C/∂b的偏导数确定。 因此，说“学习缓慢”与说这些偏导数很小是相同的。 问题在于了解为什么它们很小。 为此，让我们计算偏导数。 回想一下，我们使用由等式（6）给出的二次成本函数：

$$

$$C = \ frac {（y-a）^ 2} {2} \ tag {54}$$

其中a是在输入处使用x = 1时的神经元输出，而y = 0是所需的输出。 要直接通过重量和位移来写，请记住a =σ（z），其中z = wx + b。 使用链式规则通过重量和位移进行区分，我们获得：

$$

$$\ frac {\部分C} {\部分w} =（a-y）\ sigma'（z）x = a \ sigma'（z）\标签{55}$$

$$

$$\ frac {\部分C} {\部分b} =（a-y）\ sigma'（z）= a \ sigma'（z）\标签{56}$$

我将x = 1替换为y = 0。 要了解这些表达式的行为，让我们仔细看一下右边的σ'（z）。 回想一下S型的形状：



该图显示，当神经元的输出接近1时，曲线变得非常平坦，并且σ'（z）变小。 式（55）和（56）告诉我们，∂C/∂w和∂C/∂b变得很小。 因此学习减慢。 而且，正如我们稍后会看到的，事实上，出于同样的原因，并且在国民议会中，培训的放缓是发生的，而且这种情况更为笼统，而不仅仅是我们最简单的例子。

引入交叉熵成本函数

我们如何减慢学习速度？ 事实证明，我们可以通过用另一个值函数（称为交叉熵）代替值的二次函数来解决问题。 为了理解交叉熵，我们离开了最简单的模型。 假设我们训练具有多个输入值x ₁ ，x ₂ ，...，相应权重w ₁ ，w ₂ ，...和偏移b的神经元：



当然，神经元的输出将是a =σ（z），其中z = ∑ _j w _j x _j + b是输入的加权和。 我们将给定神经元的交叉熵代价函数定义为

$$

$$C =-\ frac {1} {n} \ sum_x \ left [y \ ln a +（1-y）\ ln（1-a）\ right] \标签{57}$$

其中n是训练数据的单位总数，总和遍及所有训练数据x，y是相应的期望输出。

方程（57）解决学习速度减慢的问题并不明显。 坦白说，称其为价值功能还不是很明显！ 在转向学习减慢之前，让我们看看在什么意义上交叉熵可以解释为价值的函数。

特别是有两个属性，可以合理地将交叉熵解释为值的函数。 首先，它大于零，即C> 0。 要看到这一点，请注意（a）（57）中总和的所有单个成员均为负，因为两个对数均取自0到1范围内的数字，并且（b）负号位于总和之前。

其次，如果神经元的实际输出接近所有训练输入x的期望输出，则交叉熵将接近零。 为了证明这一点，我们需要假设期望的输出y为0或1。通常在解决分类问题或计算布尔函数时会发生这种情况。 要了解如果不做这样的假设会发生什么，请参考本节末尾的练习。

为了证明这一点，假设对于某些输入x，y = 0且a≈0。 因此，神经元可以很好地处理此类输入。 我们看到，由于y = 0，因此表达式（57）的第一项消失了，而第二项将是-ln（1-a）≈0。 当y = 1且a≈1时，也是如此。 因此，如果实际输出接近期望值，则价值贡献将很小。

综上所述，我们得到交叉熵为正，并且当神经元更好地计算所有训练输入x的期望输出y时，交叉熵趋于零。 我们期望成本函数中同时存在这两个属性。 实际上，这两个属性都可以通过二次值来满足。 因此，对于交叉熵来说是个好消息。 但是，交叉熵代价函数具有优势，因为与二次值不同，它避免了学习速度变慢的问题。 为了看到这一点，让我们计算权重与交叉熵的值的偏导数。 代入（57）中的a =σ（z），应用链式规则两次，得到

$$

$$\ frac {\部分C} {\部分w_j} =-\ frac {1} {n} \ sum_x \ left（\ frac {y} {\ sigma（z）}-\ frac {（1-y）} {1- \ sigma（z）} \右）\ frac {\部分\ sigma} {\部分w_j} \标签{58}$$

$$

$$=-\ frac {1} {n} \ sum_x \ left（\ frac {y} {\ sigma（z）}-\ frac {（1-y）} {1- \ sigma（z）} \ right） \ sigma'（z）x_j \标记{59}$$

简化为一个公分母并进行简化，我们得到：

$$

$$\ frac {\部分C} {\部分w_j} = \ frac {1} {n} \ sum_x \ frac {\ sigma'（z）x_j} {\ sigma（z）（1- \ sigma（z）） }（\ sigma（z）-y）。 \标记{60}$$

使用sigmoid的定义σ（z）= 1 /（1 + e ^−z ）和一些代数，我们可以证明σ′（z）=σ（z）（1-σ（z））。 我将要求您在练习中进一步验证这一点，但现在，将其作为事实接受。 项σ（z）和σ（z）（1 −σ（z））被抵消，这导致

$$

$$\ frac {\部分C} {\部分w_j} = \ frac {1} {n} \ sum_x x_j（\ sigma（z）-y）。 \标记{61}$$

很棒的表情。 由此得出，训练配重的速度受σ（z）-y的控制，即受输出误差的控制。 误差越大，神经元学习越快。 可以直观地预期到这一点。 该选项避免了在类似的二次成本方程式（55）中由术语σ'（z）引起的学习速度下降。 当我们使用交叉熵时，σ'（z）项减少了，我们不再需要担心它的小。 这种减少是交叉熵代价函数所保证的特殊奇迹。 实际上，当然，这并不是一个奇迹。 稍后我们将看到，为此属性特别选择了交叉熵。

类似地，可以计算偏差的偏导数。 我不会再提供所有详细信息，但是您可以轻松地检查一下

$$

$$\ frac {\部分C} {\部分b} = \ frac {1} {n} \ sum_x（\ sigma（z）-y）。 \标记{62}$$

这再次有助于避免由于平方值（56）的类似方程中的σ'（z）而导致学习延迟。

锻炼身体

• 检查σ'（z）=σ（z）（1-σ（z））。

让我们回到我们之前玩过的牵强的示例，看看如果使用交叉熵而不是二次值会发生什么。 为了进行调整，我们从当初始权重为0.6且偏移为0.9时二次成本完美运行的情况开始。 原始文章具有交互式形式 ，您可以在其中单击“运行”按钮，查看用交叉熵替换二次值时会发生什么。

毫不奇怪，在这种情况下，神经元像以前一样被完美地训练。 现在让我们看一下 神经元曾经被卡住的情况 ，重量和位移从2.0开始。



成功！ 这次，神经元如我们所愿迅速学会了。 如果仔细观察，您会发现成本曲线的斜率最初比相应的二次值曲线的平坦区域陡。 这种越野熵给我们带来了凉爽，也不会让我们陷于我们期望神经元以最快的速度开始训练时所犯的错误非常严重的地方。

我没有说在最后的例子中使用什么训练速度。 之前，我们使用二次值η= 0.15。 在新示例中，我们应该使用相同的速度吗？ 实际上，改变成本函数，不可能确切地说出使用“相同”学习速度的含义。 这将是苹果与橙子的比较。 对于这两种成本函数，我通过寻找一种学习速度来进行实验，该速度可以让我看到正在发生的事情。 如果您仍然感兴趣，则在最新示例中，η= 0.005。

您可能会争辩说，改变学习速度会使图形失去意义。 如果我们可以任意选择学习速度，谁会关心神经元学习的速度呢？ 但是，这一反对意见没有考虑要点。 图形的含义不是学习的绝对速度，而是学习速度的变化方式。 使用二次函数时，如果神经元非常错误，则训练速度会变慢，而当神经元接近所需答案时，训练速度会变快。 利用交叉熵，当神经元犯了一个大错误时，学习会更快。 这些陈述不依赖于给定的学习速度。

我们检查了一个神经元的交叉熵。 但是，这很容易推广到具有许多层和许多神经元的网络。 假设y = y ₁ ，y ₂ ，...是输出神经元（即最后一层的神经元）的期望值，而^L ₁ ， ^L ₂ ，...是输出值本身。 然后，交叉熵可以定义为：

$$

$$C =-\ frac {1} {n} \ sum_x \ sum_j \ left [y_j \ ln a ^ L_j +（1-y_j）\ ln（1-a ^ L_j）\ right] \ tag {63}$$

这与等式（57）相同，只是现在我们的∑ _j在所有输出神经元上求和。 我不会详细分析导数，但是可以合理地假设，使用表达式（63）我们可以避免在具有许多神经元的网络中出现放慢速度。 如果有兴趣，可以对下面的问题求导。

顺便提一句，我使用的“交叉熵”一词使这本书的一些早期读者感到困惑，因为它与其他资料相矛盾。 特别是，通常为两个概率分布pj确定交叉熵
和qj为∑ _j p _j lnq _j 。 如果认为一个乙状神经元给出了由神经元a的激活和与其互补的1-a值组成的概率分布，则该定义可以与（57）相关联。

但是，如果在最后一层中有许多乙状神经元，则向量a ^L _j通常不会给出概率分布。 结果，类型∑ _j p _j lnq _j的定义_是没有意义的，因为我们不使用概率分布。 取而代之的是（63），人们可以想象如何总结每个神经元的交叉熵的总和，其中每个神经元的激活被解释为两个元素的概率分布的一部分（当然，我们的网络中没有概率元素，因此这些实际上不是概率）。 从这个意义上讲，（63）将是概率分布的交叉熵的概括。

什么时候使用交叉熵而不是二次值？ 实际上，如果您具有S型输出神经元，则交叉熵几乎总是会更好地使用。 要了解这一点，请记住，在建立网络时，我们通常使用随机过程来初始化权重和偏移量。 可能会发生这种选择，导致网络完全误解某些训练输入数据的事实-例如，输出神经元趋向于1（应设为0，反之亦然）。 如果我们使用二次值来减慢训练速度，则它根本不会停止训练，因为权重将继续在其他训练示例上进行训练，但是这种情况显然是不可取的。

练习题

• 交叉熵的一个发现是，起初可能很难记住y和a的对应作用。 很容易混淆，因为它是正确的--[ylna +（1- y）ln（1- a）]或-[alny +（1-a）ln（1- y）]。 当y = 0或1时第二个表达式会发生什么？ 这个问题会影响第一个表达式吗？ 怎么了
• 在本节开头的单个神经元讨论中，我说过对于所有训练输入数据，如果σ（z）≈y，则交叉熵很小。 , y 0 1. , (, ) y 0 1. , , σ(z)=y . ,

  $$

  $$C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)] \tag{64}$$
  。 −[ylny+(1−y)ln(1−y)] .

• . ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j) \tag{65}$$
  σ'(z ^L _j ) , . , δ ^L x

  $$

  $$\delta^L = a^L-y \tag{66}$$
  , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{67}$$
  σ'(z ^L _j ) , , , . . , .
• . , . , , , , a ^L _j = z ^L _j . , δL x

  $$

  $$\delta^L = a^L-y \tag{68}$$
  , , , ,

  $$

  $$\frac{\partial C}{\partial w^L_{jk}} = \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}$$

  $$

  $$\frac{\partial C}{\partial b^L_{j}} = \frac{1}{n} \sum_x (a^L_j-y_j) \tag{70}$$
  , , . .

MNIST

交叉熵很容易实现为使用梯度下降和反向传播教授网络的程序的一部分。我们稍后将通过开发来自MNIST的早期手写数字分类程序的改进版本network.py来进行此操作。新程序称为network2.py，它不仅包括交叉熵，还包括本章中开发的其他几种技术。同时，让我们看看我们的新程序对MNIST数字的分类情况如何。与第1章一样，我们将使用包含30个隐藏神经元和大小为10的微型数据包的网络。我们将设置学习速度η= 0.5，并学习30个时代。

正如我已经说过的，在这种情况下无法确切地说出适合的训练速度，因此我尝试了选择。的确，有一种方法可以将学习率与交叉熵和二次值进行非常粗略的启发式关联。前面我们看到，在二次值的梯度项中，还有一个附加项σ'=σ（1-σ）。假设我们平均的值σ，∫ ¹ ₀ Dσσ（1-σ）= 1/6。可以看出，对于相同的学习速率，（非常粗略的）二次成本平均学习速度要慢6倍。这表明一个好的出发点是将二次函数的学习速度除以6。当然，这根本不是严格的论据，您也不应该太在意。但有时它可能是有用的起点。

network2.py的界面与network.py略有不同，但是仍然应该清楚发生了什么。可以使用python shell中的帮助命令（network2.Network.SGD）获得network2.py上的文档。

>>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True) 

注意，顺便说一句，net.large_weight_initializer（）命令用于初始化权重和偏移量的方式与第1章中所述相同。我们需要运行它，因为稍后我们将更改默认的权重初始化。 结果，在启动所有上述命令后，我们得到的网络的工作精度为95.49％。 使用二次值，这与第一章的结果非常接近95.42％。

让我们看看使用100个隐藏神经元和交叉熵，其余保持不变的情况。 在这种情况下，准确度是96.82％。 这是对第一章结果的重大改进，在第一章中，我们使用二次值获得了96.59％的精度。 变化似乎很小，但认为误差从3.41％降至3.18％。 也就是说，我们消除了大约1/14的错误。 很好

很好的是，与二次值相比，交叉熵成本函数可以为我们提供相似或更好的结果。 但是，他们并没有明确证明交叉熵是最佳选择。 事实是，我根本没有尝试选择超参数-训练的速度，迷你包装的大小等。 为了使改进更具说服力，我们需要适当地解决它们的优化问题。 但是结果仍然鼓舞人心，并且我们的理论计算证实了交叉熵比二次成本函数更好。

因此，整章以及原则上将贯穿本书的其余部分。 我们将开发新技术，对其进行测试，并获得“改进的结果”。 当然，很高兴看到这些改进。 但是解释它们总是很困难。 只有认真研究优化所有其他超参数之后，我们才能看到改进，这才具有说服力。 这是一项相当复杂的工作，需要大量的计算资源，通常我们不会进行如此详尽的调查。 相反，我们将在上述非正式测试的基础上进一步发展。 但是您需要记住，这样的测试并不是明确的证据，并在参数开始失败时仔细监视这些情况。

到目前为止，我们一直在详细讨论交叉熵。 如果对MNIST的结果进行很小的改进，为什么还要浪费这么多的精力呢？ 在本章的后面，我们将看到其他技术，尤其是正则化，它们将提供更强大的改进。 那么，为什么我们要关注交叉熵呢？ 特别是因为交叉熵是一种常用的价值函数，因此值得一读。 但是更重要的原因是神经元的饱和度是神经网络领域的重要问题，在本书中我们将不断提到。 因此，我对交叉熵进行了详尽的讨论，因为这是一个很好的实验室，可以开始了解神经元的饱和度以及如何解决该问题。

交叉熵是什么意思？ 它来自哪里？

我们对交叉熵的讨论围绕代数分析和实际实现。 这很有用，但是结果是，更广泛的概念性问题仍然没有答案，例如：交叉熵是什么意思？ 有没有直观的方式展示它？ 人们甚至怎么想出交叉熵呢？

让我们从最后一个开始：是什么让我们考虑交叉熵？ 假设我们发现了前面描述的学习减慢，并且意识到这是由等式（55）和（56）中的σ'（z）引起的。 稍微看一下这些方程式，我们可以考虑是否可以选择这样的成本函数，从而使σ'（z）消失。 然后_，一个训练示例的成本C = C _x将满足以下等式：

$$

$$\ frac {\部分C} {\部分w_j} = x_j（a-y）\标签{71}$$

$$

$$\ frac {\部分C} {\部分b} =（a-y）\标签{72}$$

如果我们选择一个使它们正确的值函数，那么它们宁愿简单地描述一种直观的理解，即初始误差越大，神经元学习越快。 他们还将解决减速问题。 实际上，从这些方程式开始，我们将表明可以通过简单地遵循数学本能来推导交叉熵的形式。 看到这一点，我们注意到，基于链式规则，我们得到：

$$

$$\ frac {\部分C} {\部分b} = \ frac {\部分C} {\部分a} \ sigma'（z）\标签{73}$$

在最后一个方程中使用σ'（z）=σ（z）（1 −σ（z））= a（1 − a），我们得到：

$$

$$\ frac {\部分C} {\部分b} = \ frac {\部分C} {\部分a} a（1-a）\标签{74}$$

与等式（72）相比，我们获得：

$$

$$\ frac {\部分C} {\部分a} = \ frac {a-y} {a（1-a）} \标签{75}$$

将表达式集成到a上，我们得到：

$$

$$C =-[y \ ln a +（1-y）\ ln（1-a）] + {\ rm常数} \标签{76}$$

这是一个单独的训练示例x对成本函数的贡献。 为了获得完整的成本函数，我们需要对所有训练示例进行平均，然后得出：

$$

$$C =-\ frac {1} {n} \ sum_x [y \ ln a +（1-y）\ ln（1-a）] + {\ rm常数} \标记{77}$$

这里的常数是每个训练示例的各个常数的平均值。 如您所见，方程式（71）和（72）唯一地确定了交叉熵的形状，即肉身为一个公共常数。 交叉熵并不是凭空获得的。 可以通过简单自然的方式找到她。

交叉熵的直观想法如何？ 我们如何想象呢？ 详细的解释将导致我们超越培训课程。 但是，我们可以提到起源于信息理论领域的解释交叉熵的标准方法的存在。 粗略地说，交叉熵是一种令人惊讶的度量。 例如，我们的神经元试图计算函数x→y = y（x）。 但是，它计算函数x→a = a（x）。 假设我们将a想象为y = 1的概率的神经元估计，而1-a是y的正确值为0的概率。然后，交叉熵衡量了我们平均多少会“感到惊讶”找到y的真实值。 如果我们希望有一个出路，我们就不会感到惊讶，而如果出路是出乎意料的话，我们会感到非常惊讶。 当然，我没有给出“惊奇”的严格定义，因此所有这些看起来都像是空话。 但是实际上，在信息论中，有一种确定意外的确切方法。 不幸的是，我不知道在互联网上关于这一点的良好，简短和自给自足的讨论的任何例子。 但是，如果您有兴趣进行更深入的研究，那么Wikipedia文章将提供很好的常规信息，这些信息将为您提供正确的指导。 有关详细信息，请参阅有关信息论的书中有关卡夫不等式的第5章。

挑战赛

• 我们已经详细讨论了在学习中使用二次成本函数在网络中神经元饱和时可能发生的学习减慢。 另一个可能抑制学习的因素是方程（61）中项x _j的存在。 因此，当输出x _j接近零时，相应的权重w _j将被缓慢训练。 解释为什么不可能_通过选择一些巧妙的成本函数来消除项x _j 。

Softmax（软最大功能）

在本章中，我们将主要使用交叉熵代价函数来解决学习缓慢的问题。 但是，我想根据所谓的 神经元的softmax层。 在本章的其余部分中，我们将不使用Softmax图层，因此，如果您急于赶时间，可以跳过本节。 但是，Softmax仍然值得理解，特别是因为它本身很有趣，并且特别是因为在讨论深度神经网络时，我们将在第6章中使用Softmax层。

Softmax的想法是为HC定义一种新型的输出层。 它以与S形层相同的方式开始，并形成加权输入 $$$z ^ L_j = \ sum_ {k} w ^ L_ {jk} a ^ {L-1} _k + b ^ L_j$ 。 但是，我们不使用S形来获得答案。 在Softmax层中，我们将Softmax函数应用于z ^L _j 。 根据她的说法，输出神经元j的激活a ^L _j等于：

$$

$$a ^ L_j = \ frac {e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} \标签{78}$$

在分母中，我们对所有输出神经元求和。

如果您不熟悉Softmax函数，等式（78）对您来说似乎很神秘。 我们为什么要使用这样的功能一点也不明显。 同样不明显的是，它将帮助我们解决学习速度减慢的问题。 为了更好地理解方程式（78），假设我们有一个包含四个输出神经元和四个相应加权输入的网络，我们将其指定为z ^L ₁ ，z ^L ₂ ，z ^L ₃和z ^L ₄ 。 原始文章包含交互式调整滑块，为这些滑块分配了加权输入的可能值以及相应输出激活的时间表。 研究它们的一个很好的起点是使用底部滑块增加z ^L ₄ 。





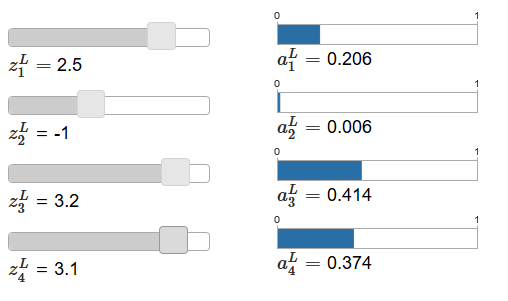
通过增加z ^L ₄ ，可以观察到相应输出激活^L ₄的增加，而其他输出激活的减少。 随着z ^L ₄的减少，a ^L ₄将减少，而所有其他输出激活将增加。 仔细观察，您会发现在这两种情况下，其他激活中的一般变化都可以完全补偿^L ₄中发生的变化。 这样做的原因是保证所有输出激活合计为1，我们可以使用等式（78）和一些代数证明：

$$

$$\ sum_j a ^ L_j = \ frac {\ sum_j e ^ {z ^ L_j}} {\ sum_k e ^ {z ^ L_k}} = 1 \标签{79}$$

结果，随着^L ₄的增加_，其余的输出激活总数必须减少相同的值，以确保所有输出激活的总和等于1。当然，对于所有其他激活，类似的语句也适用。

从等式（78）还可以得出，因为指数函数为正，所以所有输出激活都是正的。 结合上一段的观察，我们发现Softmax层的输出将是一组总数为1的正数。换句话说，Softmax层的输出可以表示为概率分布。

Softmax层的输出是概率分布的事实非常令人高兴。 在许多问题中，方便的是，能够将输出激活a ^L _j解释为由网络估计的小瓶j将是正确选项的概率。 因此，例如，在分类问题MNIST中，我们可以将^L _j解释为网络对j将成为正确数字分类概率的估计。

相反，如果输出层是S形的，那么我们绝对不能假设激活会形成概率分布。 我不会严格地证明这一点，但是可以合理地假设，在通常情况下，乙状结肠层的激活不会形成概率分布。 因此，使用S形输出层，我们将无法获得对输出激活的这种简单解释。

锻炼身体

• 举例说明，在具有S型输出层的网络中，输出激活a ^L _j并不总等于1。

我们开始对Softmax函数以及Softmax层的行为有所了解。 总结一下：方程式（78）中的指数可确保所有输出激活为正。 公式（78）的分母中的总和确保Softmax的总数为1。因此，这种公式不再显得神秘：这是确保输出激活形成概率分布的自然方法。 Softmax可以想象成一种缩放z ^L _j ，然后将它们压缩在一起以形成概率分布的方法。

练习题

• Softmax的单调性。 证明ja ^L _j /∂zL _k如果j = k _为正，如果j≠k为负。 结果，保证了z ^L _j的增加，以增加相应的输出激活a ^L _j ，并减少所有其他输出激活。 我们已经使用滑块的示例从经验上看到了这一点，但是这种证明将是严格的。
• 非本地性Softmax。 乙状结肠层的一个好特征是输出a ^L _j是相应加权输入a ^L _j =σ（z ^L _j ）的函数。 解释一下为什么Softmax层不是这种情况： ^L _j的任何输出激活取决于所有加权输入。

挑战赛

• 反转Softmax图层。 假设我们有一个带有输出Softmax层的NS，并且激活^L _j是已知的。 证明相应的加权输入的形式为z ^L _j = ln a ^L _j + C，其中C是一个独立于j的常数。

学习减速问题

我们已经非常熟悉神经元的Softmax层。 但是到目前为止，我们还没有看到Softmax层如何使我们解决学习速度减慢的问题。 为了理解这一点，让我们基于“对数似然”定义一个成本函数。 我们将使用x表示网络的训练输入，并使用y表示相应的所需输出。 然后，与此训练输入关联的LPS将是：

$$

$$C \ equiv-\ ln a ^ L_y \ tag {80}$$

因此，例如，如果我们研究MNIST图像，并且图像7进入了输入，则LPS将为-ln ^L ₇ 。 为了直观地理解这一点，我们考虑网络很好地应对识别的情况，即确保它在输入7处。在这种情况下，它将评估对应概率a ^L ₇的值接近1，因此，成本-ln ₇将很小。 相反，如果网络运行不正常，则^L ₇的可能性会较小，而^L ₇的成本-ln会更大。 因此，LPS的行为符合成本函数的预期。

减速问题呢？ 为了进行分析，我们回想起减速的主要因素是isC /∂wL _jk和∂C/∂bL _j的行为 。 我不会详细描述导数的捕获-我将要求您在任务中执行此操作，但是使用一些代数可以证明：

$$

$$\ frac {\部分C} {\部分b ^ L_j} = a ^ L_j-y_j \标签{81}$$

$$

$$\ frac {\部分C} {\部分w ^ L_ {jk}} = a ^ {L-1} _k（a ^ L_j-y_j）\标签{82}$$

我在这里使用了一些符号，并且我使用的“ y”与上一段略有不同。 y表示所需的网络输出-即，如果输出为“ 7”，则输入为图像7。在这些等式中，y表示对应于7的输出激活向量，即除7中的单位为零外，所有零的向量。的位置。

这些方程与我们在交叉熵的早期分析中获得的相似表达式相同。 比较例如方程式（82）和（67）。 这是相同的方程式，尽管后者是在训练示例中平均的。 并且，与第一种情况一样，这些表达式保证了学习不会减慢。 可以想象，具有LPS的输出Softmax层与基于交叉熵的具有S型输出和成本的层非常相似。

鉴于它们的相似性，应该使用什么-S型输出和交叉熵，或者Softmax输出和LPS？ 实际上，在很多情况下，这两种方法都行之有效。 尽管在本章的后面，我们将使用S型输出层，其成本基于交叉熵。 稍后，在第6章中，有时会使用Softmax输出和LPS。 进行更改的原因是使以下某些网络与某些有影响力的研究论文中发现的网络更加相似。 从更一般的角度来看，当您需要将输出激活解释为概率时，应使用Softmax和LPS。 这并非总是必要的，但是在分类问题（例如MNIST）中很有用，其中包括不相交的类。

任务

• 导出方程式（81）和（82）。
• Softmax这个名字来自哪里？ 假设我们更改Softmax函数，以便通过等式给出输出激活

  $$

  $$a ^ L_j = \ frac {e ^ {c z ^ L_j}} {\ sum_k e ^ {c z ^ L_k}} \标签{83}$$
  其中c是一个正常数。 请注意，c = 1对应于标准Softmax函数。 但是使用不同的c值，我们得到了另一个在质量上仍然与Softmax类似的函数。 证明输出激活形成概率分布，这与常规Softmax一样。 假设我们使c非常大，即c→＆inf;。 输出激活a ^L _j的极限值是多少？ 解决此问题后，应该清楚为什么将c = 1的函数视为最大函数的“软化版本”。 这是术语softmax的来源。
• 使用Softmax和LPS进行反向传播。 在上一章中，我们推导了包含乙状结肠层的网络的反向传播算法。 为了将该算法应用于网络层和Softmax层，我们需要导出误差^δL j∂C/∂zL _j的表达式。 证明合适的表达是

  $$

  $$\ delta ^ L_j = a ^ L_j -y_j \标签{84}$$
  使用此表达式，我们可以使用输出的Softmax层和LPS将反向传播算法应用于网络。

再培训和正规化

曾经有人要求诺贝尔奖获得者恩里科·费米（Enrico Fermi）对一些同事提出的解决重要的未解决物理问题的数学模型提出意见。 该模型与实验完全吻合，但费米对此表示怀疑。 他询问其中可以更改多少个自由参数。 “四个，”他们告诉他。 费米回答：“我记得我的朋友约翰尼·冯·诺伊曼（Johnny von Neumann）多么喜欢说，用四个参数可以将一头大象推到那里，而用五个参数可以使他摇动树干。”

当然，历史的意义在于，具有大量自由参数的模型可以描述令人惊讶的各种现象。即使这样的模型可以很好地处理可用数据，也不会自动使其成为一个好的模型。这可能只是意味着该模型有足够的自由来描述几乎任何给定大小的数据集，而无需揭示现象的主要思想。发生这种情况时，该模型可以很好地处理现有数据，但不能推广新情况。对模型的真实测试是它在从未遇到过的情况下做出预测的能力。

费米和冯·诺依曼对具有四个参数的模型表示怀疑。我们的NS具有30个隐藏的神经元，用于MNIST数字的分类，具有近24,000个参数！这些是很多参数。我们的带有100个隐藏神经元的NS具有近80,000个参数，而这些参数的高级深层NS有时具有数百万甚至数十亿个。我们可以相信他们的工作成果吗？

让我们使网络复杂化一个新的情况，使这个问题复杂化。我们将使用具有30个隐藏神经元和23,860个参数的NS。但是我们不会使用所有50,000张MNIST图像来训练网络。取而代之的是，我们仅使用前1000个。使用有限集会使泛化问题更加明显。我们将像以前一样使用基于交叉熵的成本函数进行学习，学习速度为η= 0.5，最小数据包大小为10。但是，我们将研究400个时代，这比以前稍微多了，因为有训练示例我们没有很多。让我们使用network2看一下成本函数如何变化：

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, ... monitor_evaluation_accuracy=True, monitor_training_cost=True) 

使用结果，我们可以在训练网络时建立成本变化的图表（图表是使用overfitting.py程序制作的）：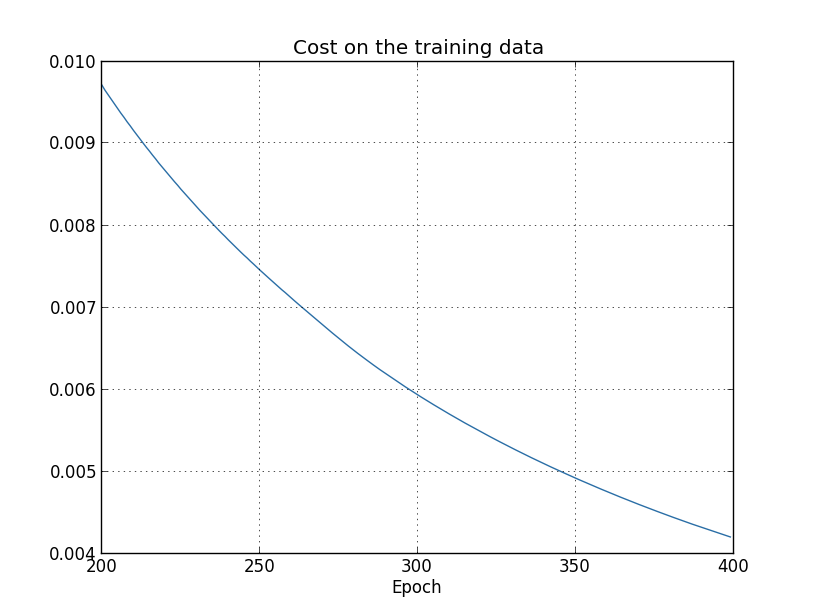



看起来令人鼓舞，正如预期的那样，成本正在平稳下降。请记住，我只显示了从200到399的时期。结果，我们放大地看到了训练的后期阶段，正如我们稍后将看到的那样，所有最有趣的事件都会发生。

现在，让我们看看验证数据的分类准确性如何随时间变化：



然后我再次增加了时间表。在前200个时代（此处看不见），准确性提高到近82％。然后训练逐渐变慢。最终，在第280年代左右，分类准确性停止提高。在以后的时代中，在第280个时代达到的精度值附近仅观察到很小的随机波动。将此与上一张图表进行比较，在该图表上与训练数据相关的成本正在逐渐降低。如果仅研究此成本，则似乎该模型正在改进。但是，使用测试数据的结果告诉我们，这种改进只是一种幻想。就像费米不喜欢的模型一样，我们在280年代后的网络研究不再推广到验证数据。因此，该培训不再有用。我们说，在280年代之后，网络正在重新训练，或过度拟合。

您可能想知道我不是根据培训数据而不是根据验证数据分类的准确性来研究成本的问题。换句话说，也许问题在于我们正在将苹果与橙子进行比较。如果将培训数据的成本与验证成本进行比较，即比较可比较的指标，将会发生什么？也许我们可以比较训练数据和测试数据的分类准确性？实际上，无论如何进行比较，都会出现相同的现象。但是细节正在改变。例如，让我们看一下验证数据的值：



可以看出，尽管训练数据的成本在不断提高，但直到15世纪左右，验证数据的成本才有所提高，然后开始完全恶化。这是再训练模型的另一个标志。但是，出现了一个问题，我们应该考虑在哪个时代开始进行再培训胜于培训（15或280）？从实践的角度来看，我们仍然对提高验证数据分类的准确性感兴趣，而成本只是分类准确性的中介。因此，考虑到280年的时代是有意义的，在那之后，再培训开始盛行于国民议会的培训。

训练数据分类的准确性可以看出再训练的另一个迹象：



准确性不断提高，达到100％。也就是说，我们的网络正确分类了所有1000个训练图像！同时，验证准确性仅增长到82.27％。也就是说，我们的网络仅研究训练集的特征，而根本不学习识别数字。似乎网络只是记住训练集，而不是足够了解数字以将其推广到测试集。

再培训是国民议会的一个严重问题。对于通常具有大量重量和位移的现代NS来说尤其如此。为了进行有效的培训，我们需要一种方法来确定何时进行再培训，以免再培训。而且我们也希望能够减少再培训的影响。

检测再培训的一种明显方法是使用上述方法，在网络培训期间监视使用验证数据的准确性。如果我们发现验证数据的准确性不再提高，则必须停止训练。当然，严格来说，这不一定是再培训的标志。也许同时处理测试和培训数据的准确性将停止提高。然而，采用这样的策略将防止再培训。

我们将使用此策略的一个小变化。回想一下，当我们将数据加载到MNIST时，我们将它们分为三组：

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() 

到目前为止，我们已经使用了training_data和test_data，并忽略了validate_data [confirming]。 Validation_data包含10,000张图像，这与MNIST训练集的50,000张图像和验证集的10,000张图像都不相同。我们将使用validation_data而不是使用test_data来防止过度拟合。为此，我们将使用与上述test_data几乎相同的策略。也就是说，我们将在每个时代结束时计算validation_data的分类准确性。一旦validation_data的分类精度已满，我们将停止学习。此策略称为“提前停止”。当然，在实践中，我们将无法立即发现准确性已得到满足。取而代之的是，我们将继续进行培训，直到确定这一点（并决定当您需要停下来时，这并不总是那么容易，您可以为此使用或多或少的激进方法。

为什么使用validation_data而不是test_data来防止重新训练？使用validation_data评估超参数的不同选择是更通用的策略的一部分，这些选择包括学习的时期数，学习的速度，最佳的网络体系结构等。我们使用这些估计来查找超参数并为其分配适当的值。尽管我还没有提到这一点，但部分原因是因为我在本书前面的示例中选择了超参数。

当然，此评论不能回答为什么我们使用validation_data而不是test_data来防止过度拟合的问题。它只是替换了一个更普遍的问题的答案-为什么我们使用validation_data而不是test_data选择超参数？要了解这一点，请记住，在选择超参数时，我们很可能必须从各种选项中进行选择。如果我们根据来自test_data的等级分配超参数，则可能会针对test_data专门定制此数据。也就是说，我们可以从test_data中找到非常适合特定数据的特定特征的超参数，但是，我们的网络操作不会被推广到其他数据集。我们通过使用validation_data选择超参数来避免这种情况。然后，在收到我们需要的GP之后，我们使用test_data进行最终的准确性评估。这使我们充满信心，我们用test_data得到的结果是NS泛化程度的真实度量。换句话说，辅助数据就是这样的特殊训练数据，可以帮助我们学习良好的GP。这种定位GP的方法有时称为保留方法，因为validate_data与training_data分开“持有”。

实际上，即使在评估了test_data的工作质量之后，我们还是会改变主意，尝试使用不同的方法（也许是不同的网络体系结构），其中将包括搜索一组新的GP。在这种情况下，是否存在不必要地适应test_data的危险？我们是否需要可能无限数量的数据集，以确保我们的结果能被很好地推广？通常，这是一个深刻而复杂的问题。但是出于我们的实际目的，我们不会对此太担心。如上所述，我们只是使用基于training_data，validation_data和test_data的简单保留方法简单地深入研究。

到目前为止，我们一直在考虑使用1000个训练图像进行再训练。如果我们使用50,000张图像的完整训练集会发生什么？我们将所有其他参数保持不变（30个隐藏的神经元，学习速度0.5，小数据包大小10），但是我们将使用所有50,000张图片研究30个时代。这是一张图表，显示了训练数据和测试数据分类的准确性。请注意，这里我使用了验证数据而不是验证数据，以便更轻松地将结果与早期图形进行比较。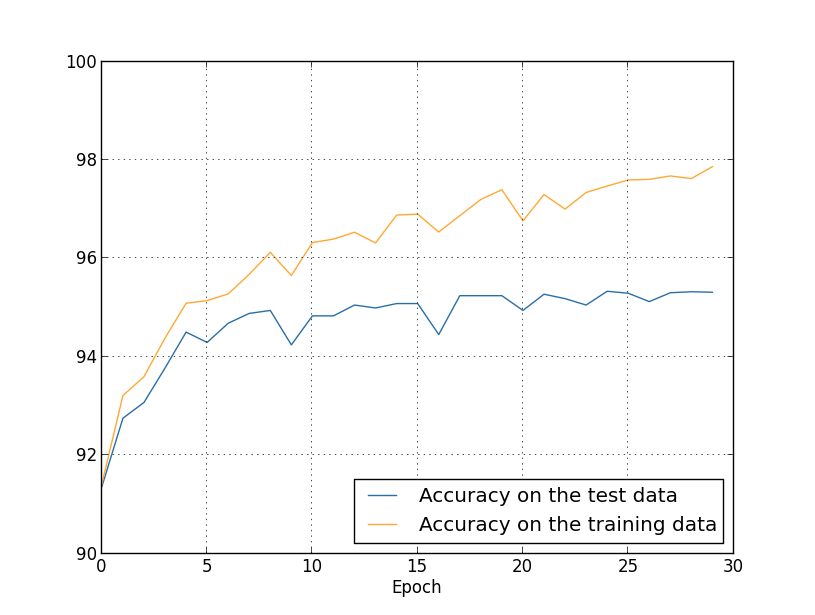



可以看出，与使用1000个训练示例相比，测试和训练数据上的准确性指标保持彼此更接近。特别是，最佳分类精度为97.86％，仅比验证数据的95.33％高2.53％。相比之下，早早下跌了17.73％！正在进行再培训，但大大减少了。从培训到测试数据，我们的网络可以更好地编译信息。通常，减少再训练的最佳方法之一是增加训练数据量。有了足够的训练数据，即使是非常大的网络也很难进行训练。不幸的是，获取训练数据非常昂贵和/或困难，因此此选项并不总是可行的。

正则化

增加训练数据量是减少再训练的一种方法。还有其他减少培训的方法吗？一种可能的方法是减小网络大小。确实，大型网络比小型网络具有更大的潜力，因此我们不愿诉诸此选项。

幸运的是，即使我们已经确定了网络和训练数据的大小，还有其他技术可以减少再训练。它们被称为正则化技术。在本章中，我将介绍一种最流行的技术，有时称为弱化权重或使L2正则化。她的想法是在成本函数中添加一个称为正则化成员的额外成员。这是带有正则化的交叉熵：

$$

$$C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2 \tag{85}$$

第一项是交叉熵的常用表达。但是我们增加了第二个，即所有网络权重的平方和。它由因子λ/ 2n缩放，其中λ> 0是正则化参数，而n通常是训练集的大小。我们将讨论如何选择λ。还值得注意的是，正则化项中不包括偏差。关于它下面。

当然，可以规范其他成本函数，例如二次函数。这可以通过类似的方式完成：

$$

$$C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2 \tag{86}$$

在两种情况下，我们都可以将正则化成本函数写为

$$

$$C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \tag{87}$$

其中C ₀是未经正则化的原始成本函数。

从直觉上很明显，在所有其他条件相同的情况下，正则化的目的是说服网络选择较小的权重。大的权重只有在它们显着改善成本函数的第一部分时才有可能。换句话说，正则化是在找到较小的权重和最小化初始成本函数之间做出折衷选择的一种方式。重要的是，折衷的这两个要素取决于λ的值：当λ小时，我们倾向于最小化原始成本函数；当λ大时，我们倾向于较小的权重。

根本不明白为什么选择这样的折衷办法应该有助于减少再培训！但事实证明这很有帮助。在下一节中，我们将弄清楚它为什么有帮助。但是首先，让我们来看一个显示正则化确实可以减少重新训练的示例。

为了构造一个例子，我们首先需要了解如何将具有随机梯度下降的训练算法应用于正则化NS。特别是，我们需要知道如何计算网络中所有权重和偏移量的偏导数∂C/∂w和∂C/∂b。在将等式（87）中的偏导数取后，得到：

$$

$$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}$$

$$

$$\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b} \tag{89}$$

成员∂C ₀ /∂w和∂C ₀ /∂w可以通过或计算，如在前面的章节中描述。我们看到，计算正则化成本函数的梯度很容易：您只需要照常使用OP，然后将λ/ nw加到所有权重项的偏导数上即可。位移的偏导数不变，因此，通过梯度下降学习位移的规则与通常的规则没有什么不同：

$$

$$b \rightarrow b -\eta \frac{\partial C_0}{\partial b} \tag{90}$$

重量训练规则变成：

$$

$$w \rightarrow w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}$$

$$

$$= \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w} \tag{92}$$

一切都与通常的梯度下降法则相同，除了我们首先将权重w缩放1-ηλ/ n。这种缩放有时称为减肥，因为它减轻了体重。乍一看，权重似乎不可避免地趋于零。但这不是这样，因为如果这导致不规则成本函数的减少，则另一个术语可能导致权重增加。

好的，让梯度下降像这样工作。随机梯度下降呢？以及，如在nonregularized变随机梯度下降，我们可以估算∂C ₀通过平均微型包米训练样例/∂w。因此，随机梯度下降的正则化学习规则变为（参见等式（20））：

$$

$$w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w} \tag{93}$$

其中小包装中的训练示例x的总和，而C _x是每个训练示例的不规则成本。除重量损失因子1-ηλ/ n之外，其他所有内容均与随机梯度下降的通常规则相同。最后，为了完成图片，让我写下一个用于偏移的正则化规则。自然，它与不规则情况完全相同（请参见等式（21））：

$$

$$b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b} \tag{94}$$

迷你包装中用于培训示例x的金额。

让我们看看正规化如何改变国民议会的效力。我们将使用一个包含30个隐藏神经元的网络，一个大小为10的微型数据包，学习速度为0.5以及具有交叉熵的成本函数。但是，这次我们使用正则化参数λ= 0.1。在代码中，我将此变量命名为lmbda，因为lambda字在python中用于与本主题无关的内容。我还再次使用了test_data而不是validation_data。但是我决定使用test_data，因为结果可以直接与我们早期的不规则结果进行比较。您可以轻松地更改代码，以使其使用validation_data，并确保结果相似。

 >>> import mnist_loader >>> training_data, validation_data, test_data = \ ... mnist_loader.load_data_wrapper() >>> import network2 >>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data[:1000], 400, 10, 0.5, ... evaluation_data=test_data, lmbda = 0.1, ... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, ... monitor_training_cost=True, monitor_training_accuracy=True) 

与早期情况一样，训练数据的成本也在不断下降，而没有进行正规化：



但是这一次，test_data的准确性在所有400个时代中都在不断提高：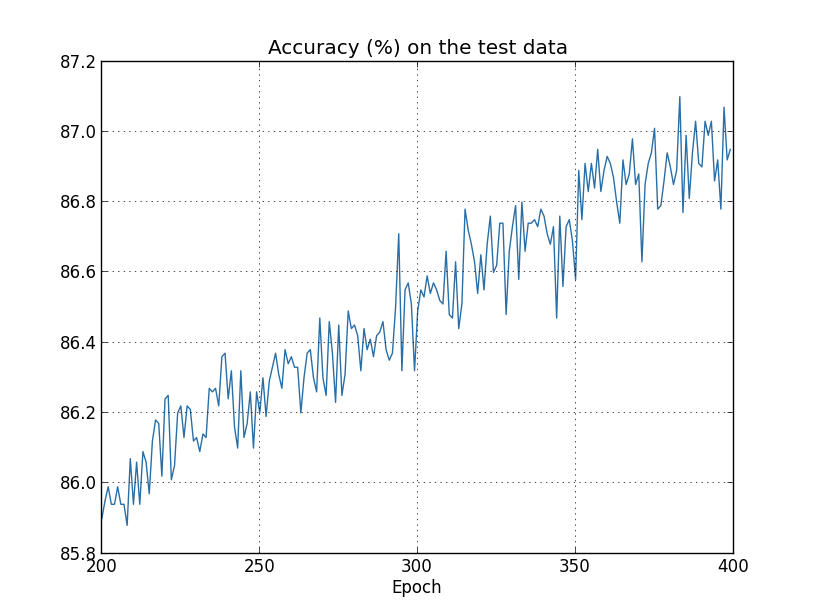



显然，正规化抑制了再训练。此外，与未进行正则化的情况下获得的峰的82.27％相比，其准确度已显着提高，并且峰的分类准确度达到87.1％。总的来说，我们几乎可以肯定，经过400个时代的学习，我们可以获得更好的成绩。从经验上讲，正则化似乎可以使我们的网络更好地概括知识，并显着降低再培训的影响。

如果我们离开仅使用1,000张教学图片的人工环境，然后返回到完整的50,000张图像，会发生什么情况？当然，我们已经看到，使用全套50,000张图像，再培训是一个小得多的问题。正则化有助于改善结果吗？让我们保留先前的超参数值-30个时期，速度0.5，最小数据包大小10。但是，我们需要更改正则化参数。事实是，训练集的大小n从1000跃升至50000，这改变了权重1的衰减因子-ηλ/ n。如果我们继续使用λ= 0.1，这意味着权重的削弱程度要小得多，因此，正则化的影响会降低。我们通过接受λ= 5.0对此进行补偿。

好的，让我们通过首先重新初始化权重来训练我们的网络：

 >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, ... evaluation_data=test_data, lmbda = 5.0, ... monitor_evaluation_accuracy=True, monitor_training_accuracy=True) 

我们得到的结果是：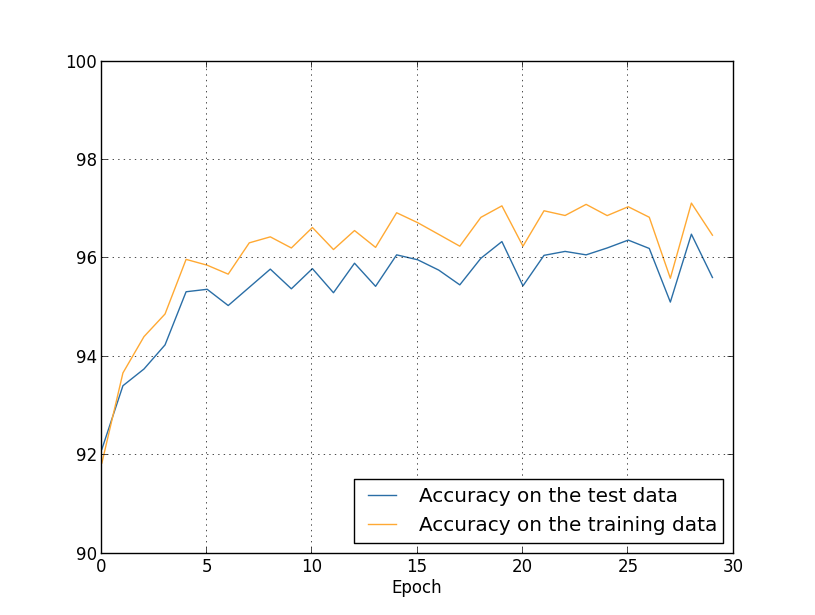



很多令人愉快的事情。首先，我们对验证数据的分类准确性已从无正则化的95.49％增长到有正则化的96.49％。这是一个重大改进。其次，可以看出，训练和测试集上的工作结果之间的差距比以前要低得多，不到1％。差距仍然很大，但我们显然在减少再培训方面取得了重大进展。

最后，看看使用100个隐藏神经元和正则化参数＆lambda = 5.0时获得的分类精度。我不会对再培训进行详细的分析，这只是出于娱乐目的，以了解使用我们的新技巧（具有交叉熵和L2正则化的代价函数）可以实现多少精度。

 >>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost) >>> net.large_weight_initializer() >>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0, ... evaluation_data=validation_data, ... monitor_evaluation_accuracy=True) 

最终结果是对支持数据的分类精度为97.92％。与具有30个隐藏神经元的情况相比，有了很大的飞跃。您可以进行更多微调，以η= 0.1和λ= 5.0的60个周期开始该过程，并克服98％的障碍，在支持数据上达到98.04的精度。 152行代码不错！

我将正则化描述为减少重新训练并提高分类准确性的一种方法。但是，这些并不是其唯一的优势。从经验上讲，尝试过多次启动我们的网络MNIST，每次更改权重后，我发现没有规则化的启动有时会“卡住”，很明显落入成本函数的局部最小值中。结果，不同的发射有时会产生非常不同的结果。相反，正则化使您可以轻松获得可重复的结果。

为什么会这样呢？启发式地，当成本函数没有正则化时，在所有其他条件相同的情况下，权重向量的长度很可能会增长。随着时间的流逝，这可能会导致很大的权重向量。由于这个原因，比例尺的矢量可能会卡住，并显示在大致相同的方向上，这是因为由于梯度下降而导致的变化在矢量的长度较长时仅会导致方向上的微小变化。我相信由于这种现象，我们的训练算法很难正确地研究权重空间，因此很难找到成本函数的最小值。