我遇到了一个名为
Enscombe Quartet （
Anscombe ）”（
英文版 ）的任务。
图1显示了4个随机函数的表格分布（摘自Wikipedia）。
图 1.四个随机函数的表分布图2显示了这些随机函数的分布参数
图 2.四个随机函数的分布参数及其图如图3所示。
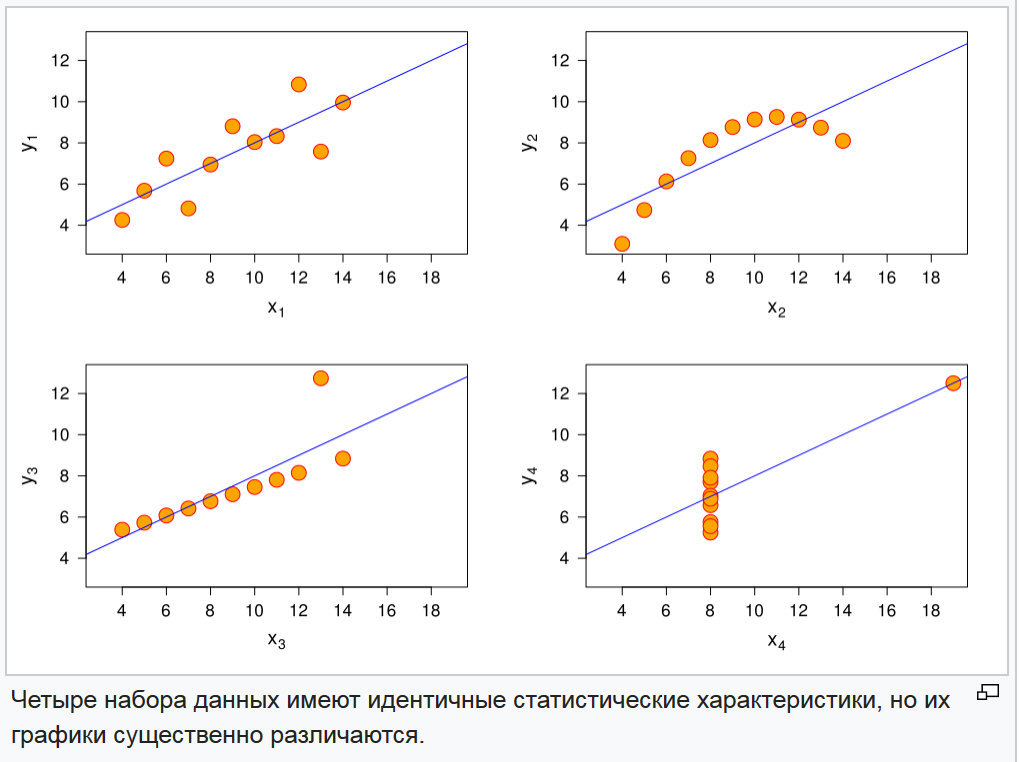图 3.四个随机函数的图通过比较高阶矩及其归一化指标：
不对称系数和
超额系数，可以非常轻松地解决区分这些功能的问题。 这些指标如图4所示。
图 4.三阶和四阶矩的指标以及四个随机函数的不对称性和超额系数从图4的表中可以看出，所有功能的这些指标的组合是不同的。
第一个结论自然表明与点的相对位置有关的信息存储在分布参数中的级别高于随机分布的方差。
许多分析人员正在尝试隔离大数据中的特定回归方程式，到目前为止，今天，这是一种选择残差最小的方程式的方法。 没什么可添加的。 但是我提请注意以下事实：这就是所有信息，信息具有
熵的指标。 当信息完全确定为白噪声时，它的熵为0。 并且传输通道中的白噪声具有均匀的分布。
当需要分析数据时，最初假定它们包含需要形式化为关系的相关数据。 这表明数据不是白噪声。 即，第一阶段是回归方程的选择和残差的确定。 如果正确选择了回归，则剩余方差将服从正态分布定律。 让我们看看，在图5-7中，给出了均匀分布和正态分布的随机变量的熵公式。
图 5.正态分布量的微分熵公式（VV Afanasyev，
“问题与任务中的概率论”，俄罗斯联邦教育科学部，雅罗斯拉夫尔国立教育大学，以KD Ushinsky命名）
图 6.正态分布量的微分熵公式（Pugachev VS
随机函数理论及其在自动控制问题中的应用，第2版，经修订和补充。-M。：Fizmatlit，1960年-883页）。
图 7.均匀分布量的微分熵公式（Pugachev VS
随机函数理论及其在自动控制问题中的应用，第2版，修订和补充。-M.：Fizmatlit，1960年-883页）。
接下来，我们显示一个示例。 但是首先我们要考虑到四个函数中的每个函数都是超平面的坐标，即，同时我们检查了模型在多维空间中的操作。 绘制一个超立方体到平面的卷积。 该机制如图8所示。
图 8.带有卷积机制的初始数据
图 9.汇总图中的分组。
图 10.四个随机函数的分布参数和摘要分组。
考虑选择分区间隔大小的机制。 初始条件如图11所示。
图 11.划分间隔的初始条件。
条件1.在变化区域上它必须具有非零概率，因为否则，熵等于无穷大。 初始样品和残留样品均如此。
条件2.由于不可能忽略新数据等中存在异常值的可能性，因此对于极端间隔，有必要根据尾部概率的原理，根据概率分布的正常或其他公认的理论定律建立概率。
条件3.间隔步骤应在残留样品的扩散范围内提供所需的最小间隔数。
条件4.间隔数必须为奇数。
条件5.间隔的数量必须确保与为研究选择的理论分布规律可靠地一致。
图 12.其余部分在图13中定义间隔选择机制。
图 13.区间选择算法我认为主要的问题是决定是否引入尾巴间隔。 如果对于剩余色散，它看起来很自然，那么对于主系列，它则非常紧张。
图 14.在确定信息熵中处理数据值的结果结论 该工具可以在哪里使用
比较图14中表的结果指示符，可以看出它们对数据结构的更改做出了响应。 这意味着该工具具有敏感性，并允许您解决类似于Enskomb四重奏任务的问题。
毫无疑问，这些问题可以借助高阶指令来解决。 但是，信息熵的核心取决于随机变量的方差，也就是说，它是方差的第三方特征。 因此，我们可以指出使用方差分析可以得出特定结果的时间间隔。
熵的数值特性使得可以对自变量进行相关分析。 作为可能的连接体现的一个示例，如下所示：假设在从a到b的间隔内，数据序列的噪声水平显着增加，通过比较自变量的值，我们发现变量xn在进入后超过5个单位的范围内。可变，降到+5以下，噪音降低。 此外，可以进行进一步检查，如果这一假设得到证实，则在进一步的研究中，禁止变量xn超过+5。 由于在这种情况下，数据变得无用。
我假设使用此工具还有其他选择。
使用方法
在这方面，研究了“移动平均值”的自然机制，我认为通过统计分析的样本量公式获得的样本量将给出合理的滑动面积。 根据目前的分析，得出的结论是，样本量应从概率最小的最小比例中确定。 在我们的示例中，对于残差，经验间隔的最小分数为0.15909。 之所以必须这样做，是因为如果转差量中的任何间隔都为空，则在这种情况下，噪声系数将非常高，否则规则将起作用，即对数0等于负无穷大。 在正确选择样本量的情况下，该指标的先验值将表明信息结构的根本变化。