我的许多同事都面临这样的问题:为了计算某种度量标准(例如转换率),您必须验证整个数据库。 或者您需要对拥有数百万客户的每个客户进行详细研究。 即使在特制的存储库中,此类凯瑞也可以工作相当长的时间。 等待5-15-40分钟直到考虑一个简单的指标来发现您需要计算其他内容或添加其他内容并不是一件很有趣的事情。
解决此问题的一种方法是采样:我们不是试图在整个数据阵列上计算指标,而是采用一个代表我们所需指标的子集。 该示例可以比我们的数据数组小1000倍,但足以显示我们所需的数字。
在本文中,我决定演示抽样样本量如何影响最终指标误差。
问题
关键问题是:样本对“人口”的描述程度如何? 由于我们从一个公共数组中抽取样本,因此我们收到的指标是随机变量。 不同的样本将为我们提供不同的度量结果。 不同,并不意味着任何。 概率理论告诉我们,通过采样获得的度量值应围绕具有一定误差水平的真实度量值(在整个样本中得出)进行分组。 此外,我们经常遇到可以免除其他错误级别的问题。 弄清楚我们获得50%还是10%的转化是一回事,而获得结果的准确度则是50.01%vs 50.02%。
有趣的是,从理论上讲,我们在整个样本中观察到的转换系数也是一个随机变量,因为 “理论”转换率只能在无限大小的样本上计算。 这意味着即使我们在数据库中的所有观察结果实际上也给出了其准确性的转换估算值,尽管在我们看来这些计算出的数字绝对准确。 这也得出结论,即使今天的转换率与昨天不同,这并不意味着有所改变,而仅意味着当前样本(数据库中的所有观察值)来自一般人群(所有可能今天发生的和未发生的观测结果与昨天相比略有不同。 无论如何,对于任何诚实的产品或分析师而言,这应该是一个基本假设。
假设我们在0/1类型的数据库中有1,000,000条记录,它告诉我们事件是否发生了转换。 那么转换率就是1乘以100万的总和。
问题:如果我们采用大小为N的样本,那么转换率与整个样本中计算出的转换率有多少差异?
理论上的考虑
任务被简化为针对二项分布的给定大小的样本计算转换系数的置信区间。
从理论上讲,二项式分布的标准偏差为:
S = sqrt(p *(1-p)/ N)
哪里
p-转换率
N-样本数量
S-标准差
我不会从理论上考虑直接置信区间。 有一个相当复杂和令人困惑的方法,最终将标准差和置信区间的最终估计联系起来。
让我们开发一个关于标准偏差公式的“直觉”:
- 样本量越大,误差越小。 在这种情况下,误差落在反二次相关性上,即 将样本增加4倍,仅将准确性提高2倍。 这意味着在某个点上增加样本大小不会带来任何特殊的优势,并且还意味着可以使用相当小的样本获得相当高的准确性。

- 误差与转换率的值有关。 相对误差(即,误差与转换率的值之比)具有“不稳定性”的趋势,转换率越低,则该误差越大:
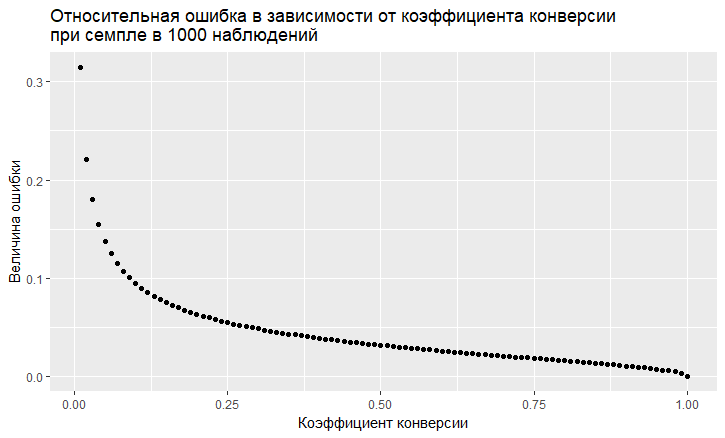
- 如我们所见,该错误以低转换率“飞上蓝天”。 这意味着,如果您对稀有事件进行采样,则需要大样本量,否则您将获得带有非常大误差的转换估算值。
造型
我们可以完全摆脱理论上的解决方案,而解决“正面”的问题。 由于有了R语言,现在这很容易做到。 要回答这个问题,我们在采样时会遇到什么错误,您只需做一千个样本,然后看看我们会遇到什么错误。
方法是这样的:
- 我们采用不同的转化率(从0.01%到50%)。
- 我们从样本中抽取10、100、1000、10000、50,000、50,000、100,000、250,000、500,000个元素的1000个样本
- 我们计算每组样本的转换率(1000个系数)
- 我们为每组样本构建一个直方图,并确定观察到的转化率分别占60%,80%和90%的程度。
R代码生成数据:
sample.size <- c(10, 100, 1000, 10000, 50000, 100000, 250000, 500000) bootstrap = 1000 Error <- NULL len = 1000000 for (prob in c(0.0001, 0.001, 0.01, 0.1, 0.5)){ CRsub <- data.table(sample_size = 0, CR = 0) v1 = seq(1,len) v2 = rbinom(len, 1, prob) set = data.table(index = v1, conv = v2) print(paste('probability is: ', prob)) for (j in 1:length(sample.size)){ for(i in 1:bootstrap){ ss <- sample.size[j] subset <- set[round(runif(ss, min = 1, max = len),0),] CRsample <- sum(subset$conv)/dim(subset)[1] CRsub <- rbind(CRsub, data.table(sample_size = ss, CR = CRsample)) } print(paste('sample size is:', sample.size[j])) q <- quantile(CRsub[sample_size == ss, CR], probs = c(0.05,0.1, 0.2, 0.8, 0.9, 0.95)) Error <- rbind(Error, cbind(prob,ss,t(q))) }
结果,我们得到了下表(稍后将提供图形,但是在表中更清楚可见)。
让我们看看转化率为10%且转化率为0.01%较低的情况,因为 采样工作的所有功能都清晰可见。
转换率为10%时,图片看起来非常简单:

点是5-95%置信区间的边缘,即 制作样本时,我们将在90%的情况下在此间隔内获得样本的CR。 垂直标度-样本量(对数标度),水平标度-转化率值。 竖线是“真实” CR。
我们看到了与从理论模型中看到的相同的结果:随着样本大小的增加,准确性提高了,并且收敛很快,样本得到的结果接近“真实”。 总共1000个样本中,我们有8.6%-11.7%,足以完成许多任务。 而在一万个中已经有9.5%-10.55%。
罕见事件会使事情变得更糟,这与理论相符:

在0.01%的低转换率下,问题在于对100万个观测值的统计,而对于样本,情况甚至更糟。 这个错误是巨大的。 对于不超过10,000个的样本,该度量原则上是无效的。 例如,在10个观测值的样本中,我的生成器仅获得0次转换1000次,因此只有1点。 在10万时,我们的散点从0.005%到0.0016%,即我们可以通过这种采样获得几乎一半的系数。
还值得注意的是,当您观察到如此小的规模转换为一百万次试用时,那么您自然就有一个很大的自然错误。 由此得出的结论是,必须在非常大的样本上得出关于此类罕见事件动态的结论,否则,您就只能追逐鬼影,数据中的随机波动。
结论:
- 抽样工作方法以获取估计
- 样品精度随着样品量的增加而增加,而随着转化率的降低而降低。
- 可以为您的任务建模估计的准确性,从而为您自己选择最佳采样。
- 重要的是要记住,罕见事件的采样效果不佳
- 通常,很难分析罕见事件;它们需要没有样本的大数据样本。