将图像转换为声音-您会听到什么？

哈Ha

该站点上最近的出版物描述了一种设备，该设备可使盲人“看到”图像，并使用声波对其进行转换。 从技术角度来看，该文章中没有任何细节（ 如果一百万的想法被盗了该怎么办 ），但是这个概念本身似乎很有趣。 有了信号处理方面的经验，我决定自己进行实验。



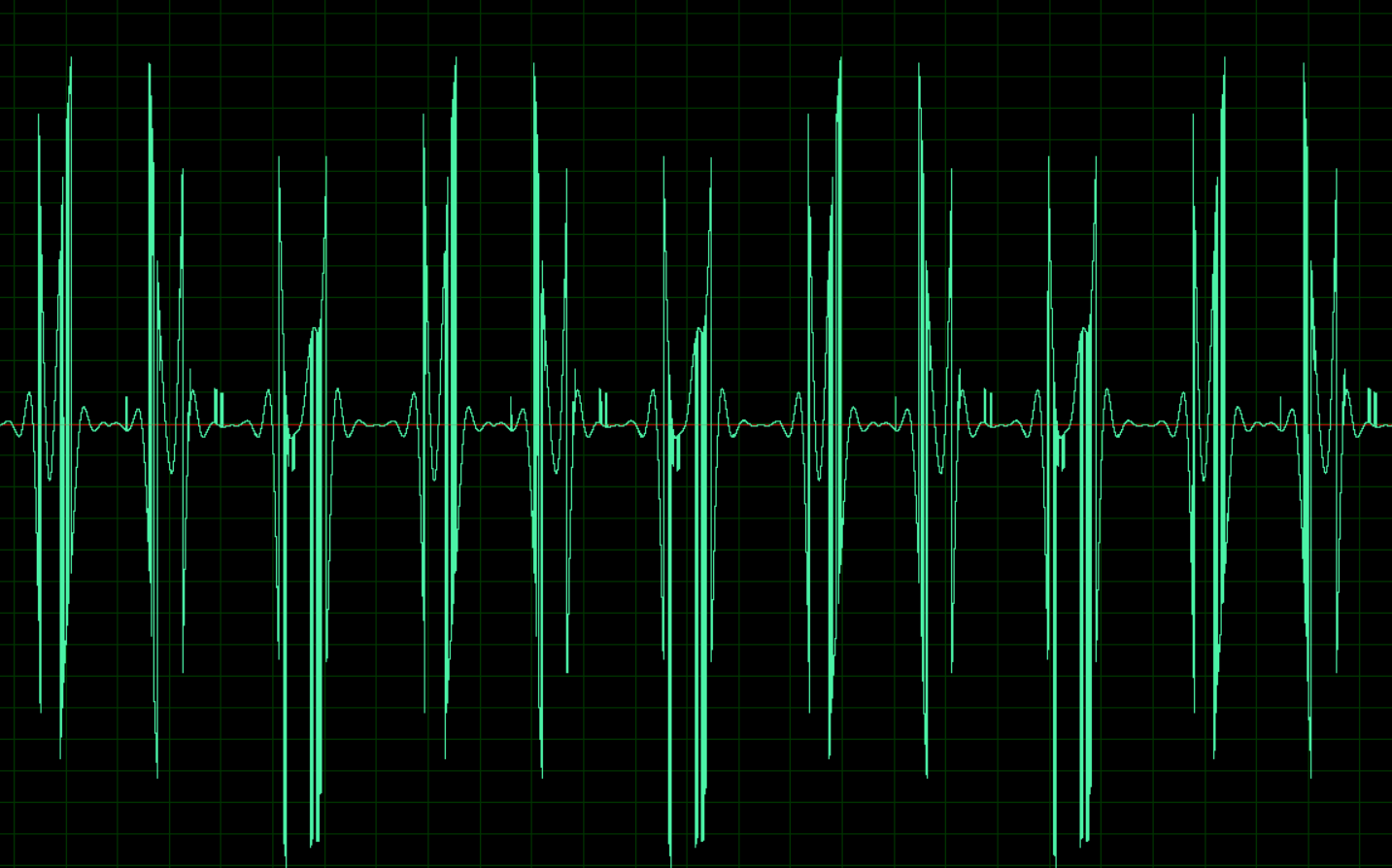
它带来了什么，细节和文件示例。

将2D转换为1D

等待我们的第一个显而易见的任务是将二维“平面”图像转换为“一维”声波。 如该文章评论中所建议，为此使用希尔伯特曲线很方便。

它本质上类似于一个分形，其思想是随着图像分辨率的提高，对象的相对位置不会改变（如果对象位于图像的左上角，则它将保留在那里 ）。 希尔伯特曲线的不同尺寸可以为我们提供不同的图像：N = 5时为32x32，N = 6时为64x64，依此类推。 通过沿着该曲线“遍历”图像，我们得到一条线，即一维对象。

下一个问题是图片的大小。 我直觉上想拍摄更大的图像，但是有一个很大的“但是”：即使图片是512x512，也就是262144像素。 如果将每个点转换为音频脉冲，则以44100的采样频率，我们将获得长达6秒的序列，而且该序列太长-必须快速更新图像，例如使用网络摄像头。 增大采样率是没有意义的；我们得到的声音是耳朵听不见的超声频率（尽管它可能对猫头鹰或蝙蝠有效）。 结果， 通过科学戳的方法选择了128x128的分辨率，这将产生0.37c长的脉冲-一方面它足够快以进行实时导航，另一方面它足以捕捉任何人耳信号形状的变化。

影像处理

第一步是下载图像，将其转换为黑白，然后缩放至所需大小。 图像大小取决于希尔伯特曲线的尺寸。

from PIL import Image from hilbertcurve.hilbertcurve import HilbertCurve import numpy as np from scipy.signal import butter, filtfilt # Create Hilbert curve dimension = 7 hilbert = HilbertCurve(dimension, n=2) print("Hilbert curve dimension:", dimension) # Maximum distance along curve print("Max_dist:", hilbert.max_h) # Maximum distance along curve print("Max_coord:", hilbert.max_x) # Maximum coordinate value in any dimension # Load PIL image f_name = "image01.png" img = Image.open(f_name) width, height = img.size out_size = hilbert_curve.max_x + 1 if width != out_size: img = img.resize((out_size, out_size), Image.ANTIALIAS) # Get image as grayscale numpy array img_grayscale = img.convert(mode='L') img_data = np.array(img_grayscale) 

下一步是形成声波。 当然，这里有很多算法和专门知识，对于测试，我只是选择了亮度分量。 当然，可能有更好的方法。

 width, height = img_grayscale.size sound_data = np.zeros(width*height) for ii in range(width*height): coord_x, coord_y = hilbert_curve.coordinates_from_distance(ii) pixel_l = img_data[coord_x][coord_y] # Inverse colors (paper-like, white = 0, black = 255) pixel_l = 255 - pixel_l # Adjust values 0..255 to 0..8192 ampl = pixel_l*32 sound_data[ii] = ampl 

从代码中，我希望一切都清楚。 axes_from_distance函数为我们完成了将坐标（x，y）转换为希尔伯特曲线上的距离的所有工作，我们将亮度值L转换并转换为颜色。

这还不是全部。 因为 图像中可能有大块相同颜色的块，这可能会导致声音中出现“直流分量”-一长串非零值，例如[100,100,100，...]。 为了去除它们，我们将一个高通滤波器（ Butterworth滤波器 ）应用于截止频率为50 Hz的阵列（与网络频率的重合是随机的）。 scipy库中有一个综合的过滤器，我们将使用它。

 def butter_highpass(cutoff, fs, order=5): nyq = 0.5 * fs normal_cutoff = cutoff / nyq b, a = butter(order, normal_cutoff, btype='high', analog=False) return b, a def butter_highpass_filter(data, cutoff, fs, order=5): b, a = butter_highpass(cutoff, fs, order) y = filtfilt(b, a, data) return y # Apply high pass filter to remove dc component cutoff_hz = 50 sample_rate = 44100 order = 5 wav_data = butter_highpass_filter(sound_data, cutoff_hz, sample_rate, order) 

最后一步是保存图像。 因为 一个脉冲的长度很短，我们将其重复10次，在接近真实的重复图像（例如从网络摄像头）时，它会更容易听见。

 # Clip data to int16 range sound_output = np.clip(wav_data, -32000, 32000).astype(np.int16) # Save repeat = 10 sound_output_ntimes = np.tile(sound_output, repeat) wav_name = "ouput.wav" scipy.io.wavfile.write(wav_name, sample_rate, sound_output_ntimes) 

结果

当然，以上算法是非常原始的。 我想检查三点-您可以区分不同的简单形状多少，以及可以估计到形状的距离。

测试1



该图像对应于以下声音信号：


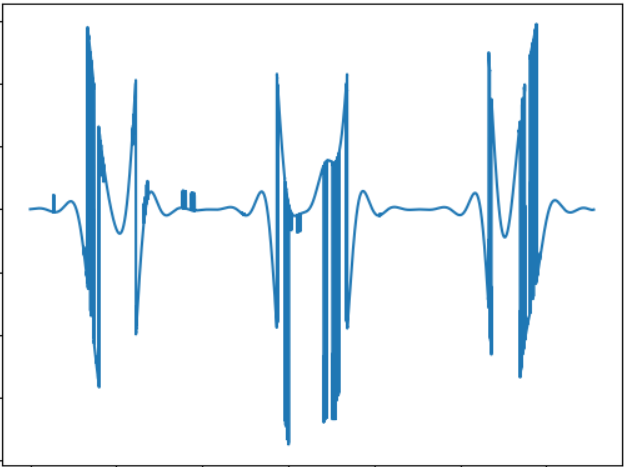
WAV： cloud.mail.ru/public/nt2R/2kwBvyRup

测试2



该测试的目的是比较不同形状的对象的“声音”。 声音信号：


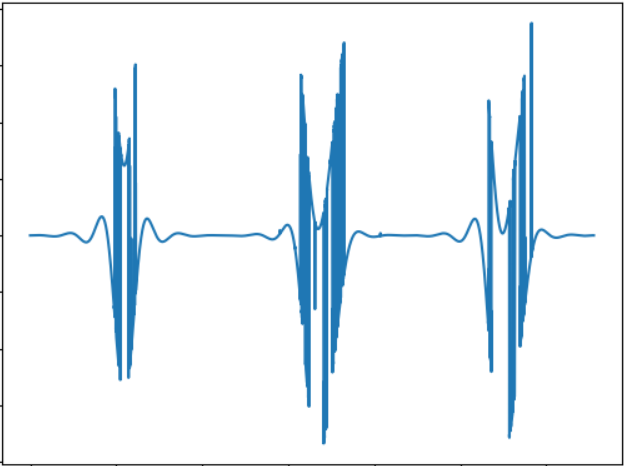
WAV： cloud.mail.ru/public/2rLu/4fCNRxCG2

您可能会注意到声音确实有所不同，并且耳朵有所不同。

测试3



测试的想法是测试较小的对象。 声音信号：


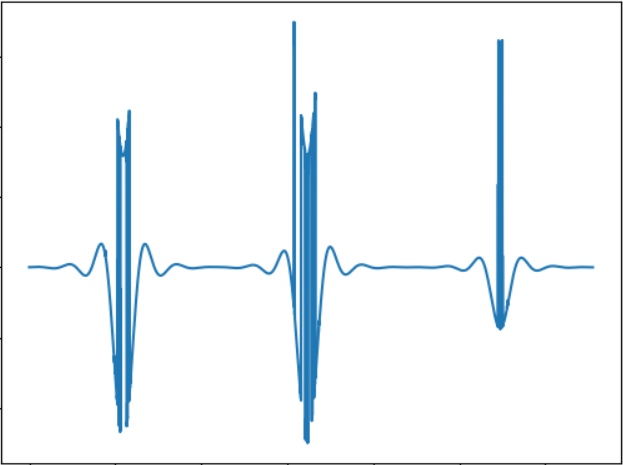
WAV： cloud.mail.ru/public/5GLV/2HoCHvoaY

原则上，物体的尺寸越小，声音中的“爆发”就越少，因此此处的依赖性非常直接。

编辑：

如评论中所建议，您可以使用傅立叶变换将图片直接转换为声音。 快速测试显示以下结果（图片相同）：
测试1： cloud.mail.ru/public/2C5Z/5MEQ8Swjo
测试2： cloud.mail.ru/public/2dxp/3sz8mjAib
测试3： cloud.mail.ru/public/3NjJ/ZYrfdTYrk

测试听起来很有趣，至少对于小方块和大方块（文件1和3）而言，听觉上的差异是显而易见的。 但是图形（1和2）的形状实际上没有区别，因此也需要考虑一些事情。 但总的来说，我更喜欢用FFT获得的声音。

结论

当然，该测试不是学位论文，而只是在几个小时的空闲时间内进行的概念验证。 但是，即使这样，它基本上也可以奏效，而且很有可能通过耳朵感受到差异。 我不知道是否有可能经过这样的声音学习在太空中导航，假设经过一些训练。 尽管有很大的改进和实验领域，例如，您可以使用立体声，这样可以更好地从不同侧面分离对象，也可以尝试将图像转换为声音的其他方法，例如，以不同的频率编码颜色等。最后，这是有希望的使用能够感知深度的3d相机（可惜，这种相机不可用）。 顺便说一下，借助简单的OpenCV代码，可以将上述算法改编为使用网络摄像头，这将使您可以对动态图像进行实验。

好吧，像往常一样，所有成功的实验。