👨🏾‍💻 🤞🏾 😯 蚱hopper密码算法：复杂 🚣🏼 🙂 ♣️

本文将详细介绍GOST R 34.12-2015中定义为Grasshopper的块加密算法。它基于什么，块密码算法的数学是什么，以及如何在Java中实现该算法。

谁，如何，何时以及为什么开发这种算法将不在本文讨论范围之内，因为在这种情况下，我们几乎没有兴趣，除了：

蚱= =库兹涅佐夫（Nechaev AND Company）。

由于密码学主要基于数学，因此进一步的解释不会引起很多问题，因此您应该首先分析构建该算法的基本概念和数学函数。

菲尔兹·加洛瓦（Fields Galois）

Galois字段的算术是多项式算术，也就是说，该字段的每个元素都是一个多项式。任何操作的结果也是该字段的元素。特定的Galois字段由固定范围的数字组成。场特性称为一些质数p。现场订单，即其元素的数量是一定的自然特征

$p ^ m$ ，其中m ϵN。对于m = 1，该字段称为简单字段。在m> 1的情况下，为了形成场，还需要生成次数为m的生成多项式；这种场称为扩展场。

（ ）

$Gf（p ^ m）$ -指定Galois油田。生成多项式是不可约的，即是简单的（类似于质数，它可以被1整除而没有余数）。由于处理任何信息都使用字节，并且字节为8位，因此将其作为字段

（ ）

$Gf（2 ^ 8）$ 和生成多项式：

$x ^ 8 + x ^ 7 + x ^ 6 + x + 1.$

但是，首先，我们将在一个更简单的领域中分析基本操作

（ ）

$Gf（2 ^ 3）$ 与生成多项式

（ ）

$f（x）= x ^ 3 + x + 1$ 。

加法运算

最简单的是加法运算，在Galois场算术中，该运算是简单的按位加法模2（R）。

我立即提请注意以下事实：这里的“ +”符号是指按位XOR的操作，而不是通常形式的加法。

HOR函数的真值表

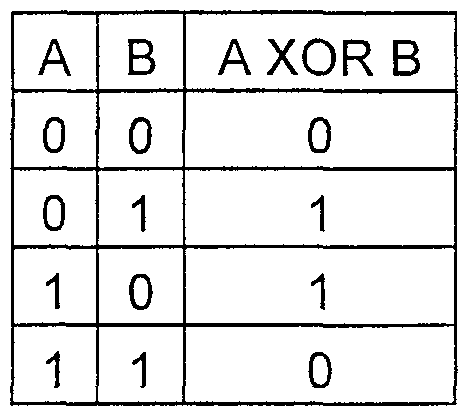
一个例子：

$5 + 3 = 101 + 011 = 110_2 = 6_ {10}$

在多项式形式中，该运算看起来像

$（x ^ 2 +1）+（x +1）= x ^ 2 + x = 110_2 = 6_ {10}$

乘法运算

要进行乘法运算，必须将数字转换为多项式形式：

$5 = 101_2 = 1 * x ^ 2 + 0 * x ^ 1 + 1 * x ^ 0 = x ^ 2 + 1$

如您所见，多项式形式的数字是一个多项式，其系数是数字的二进制表示形式中的数字值。

将多项式形式的两个数相乘：

$5 * 7 =（x ^ 2 + 1）*（x ^ 2 + x + 1）= x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x +1 =$

$= x ^ 4 + x ^ 3 + x +1 = 11011_2 = 27_ {10}$

乘法结果27不在使用的字段中。

$Gf（2 ^ 3）$ （如上所述，它由0到7组成）。为了解决这个问题，有必要使用生成多项式。

还假设x满足方程

$f（x）= x ^ 3 + x + 1 = 0$ 然后

让我们做一个乘法表：

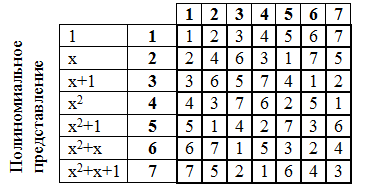
非常重要的是伽罗瓦域元素的度表。类似于乘法，也以多项式形式进行幂次提升。

一个例子：

$5 ^ 2 =（x ^ 2 + 1）^ 2 = x ^ 4 + x ^ 2 + x ^ 2 +1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 =$

$= x（x ^ 3 + x + 1）+ x ^ 2 + x + 1 = x ^ 2 + x + 1 = 111_2 = 7_ {10}$

因此，我们编译一个度表：

度表是循环的：第七度对应于零，因此第八度对应于第一个，依此类推。您可以根据需要进行检查。

在Galois字段中，有一个原始术语的概念-字段的度数包含该字段的所有非零元素的元素。可以看出，所有元素都与此条件相对应（当然，除了1之外）。但是，并非总是如此。

对于我们正在考虑的字段，即具有特征2的情况下，始终选择2。作为基本成员，鉴于其属性，可以根据基本成员的程度来表示字段的任何元素。

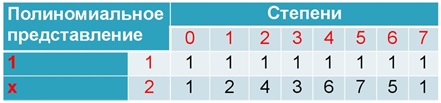
一个例子：

$5 = 2 ^ 6.7 = 2 ^ 5$

使用此属性，并考虑度表的周期性，我们将尝试再次将数字相乘：

$5 * 7 = 2 ^ 6 * 2 ^ 5 = 2 ^ {（（6 + 5）} = 2 ^ {（11mod7）} = 2 ^ 4 = 6$

结果与我们先前计算的相符。

现在让我们进行划分：

$6/5 = 2 ^ 4/2 ^ 6 = 2 ^ {（（4-6）} = 2 ^ {（（-2）mod7）} = 2 ^ 5 = 7$

获得的结果也是正确的。

好吧，为了完整起见，让我们来看一下提升能力：

$5 ^ 2 =（2 ^ 6）^ 2 = 2 ^ {{（6 * 2）} = 2 ^ {（12mod7）} = 2 ^ 5 = 7$

这样的乘法和除法方法比使用多项式的实际运算要简单得多，并且对于它们而言，不需要存储大型的乘法表，而只需存储原始字段成员的一行度。

现在回到我们的领域

$Gf（2 ^ 8）$

字段的零元素为1，第一个元素为2，从第二个元素到第254个元素的每个后续元素的计算方式为前一个元素乘以2，并且如果该元素在字段之外，即其值大于

$（2 ^ 8-1）$ 然后对数字进行异或

$195_ {10}$ ，该数字表示该字段的不可约多项式

$x ^ 8 + x ^ 7 + x ^ 6 + x +1 = 2 ^ 8 + 2 ^ 7 ++ 2 ^ 6 + 2 +1 = 451$ ，我们将此号码带入现场

$451-256 = $ 19$ 。第255个元素再次为1。因此，我们有一个包含256个元素的字段，即一个完整的字节集，并且已经分析了在该字段中执行的基本操作。

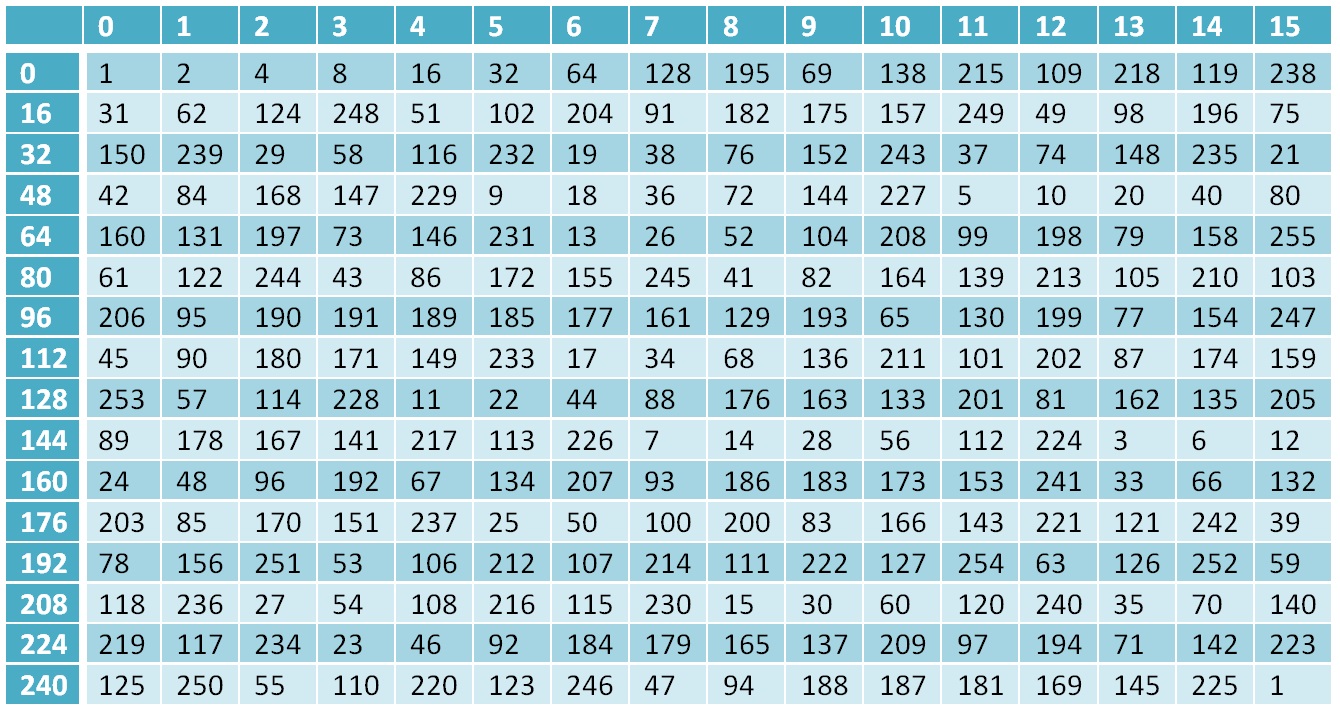
字段的二的幂表

$Gf（2 ^ 8）$

为什么需要它-Grasshopper算法中的部分计算是在Galois字段中执行的，因此，计算结果是该字段的元素。

Feistel网络

Feistel Network是1971年由IBM的Horst Feistel开发的一种块加密方法。如今，Feistel的网络已成为众多加密协议的基础。

Feistel网络使用明文块运行：

该块分为两个相等的部分-左L和右R。
左子块L通过功能f使用键K进行更改：X = f（L，K）。作为功能，可以有任何变换。
将得到的子块X与右子块R模2加，后者保持不变：X = X +R。
生成的零件被互换并粘合。

此动作序列称为Feistel电池。

图1. Feistel细胞

Feistel网络由几个单元组成。在第一单元的输出处获得的子块进入第二单元的输入，第二单元的结果子块进入第三单元的输入，依此类推。

加密算法

现在，我们已经熟悉了所使用的操作，并且可以继续讨论主要主题-Grasshopper加密算法。

该算法的基础是所谓的SP网络-替代置换网络。基于SP网络的密码在输入端接收一个块和一个密钥，并执行由替换阶段和置换阶段组成的几轮交替回合。蚱hopper执行了九轮完整回合，每个回合包括三个连续的操作：

对密钥和输入数据块应用循环密钥或按位XOR的操作；
非线性转换，即按照表简单地将一个字节替换为另一个字节；
线性变换。来自该块的每个字节在Galois字段中乘以该序列的系数之一（148、32、133、16、194、192、1、251、1、192、194、16、133、32、148、1）字节号（为从15号到0号的序列号提供了一个序列，如图所示）。字节以模2方式加在一起，并且该块的所有16个字节都向低位移位，并且将写入的结果数替换为读取的字节。

最后的第十轮未完成，仅包括第一个XOR操作。

Grasshopper是一种块算法，适用于128位或16字节长的数据块。密钥长度为256位（32字节）。

图2.数据块的加密和解密方案

该图显示了操作顺序，其中S是非线性变换，L是线性变换，Ki是圆键。问题立即出现-圆形键从何而来。

回合密钥形成

迭代（或回合）密钥是基于主密钥通过某些转换而获得的，众所周知，其长度为256位。此过程首先将主密钥分成两半，这样就获得了第一对圆形密钥。 Feistel网络的八次迭代用于生成每个后续的配对密钥，在每次迭代中使用一个常数，该常数是通过将算法的线性变换应用于迭代次数的值来计算的。

获取迭代（圆形）密钥的方案

如果我们回想一下图1，那么左子块L是原始键的左半部分，右子块R是原始键的右半部分，K是常数Ci，函数f是操作序列R XOR Ci，非线性变换，线性变换。

使用迭代序列号的L变换来获得迭代常数Ci。

因此，为了加密文本块，我们首先需要计算32个迭代常数，然后根据该密钥计算10个回合密钥，然后执行图2所示的操作序列。

让我们从计算常量开始：
第一常量

$C_1 = 1_ {10} = 00000001_2 = 01_ {16}$ ，但是，我们算法中的所有变换都是使用16个字节长的块执行的，因此有必要用该块的长度来补充常量，即在右边添加15个零字节，我们得到

$C_1 = 01000000000000000000000000000000$

将其乘以以下序列（1，148，32，133，16，194，192，1，251，1，192，194，16，133，32，148），如下所示：

$a_ {15} = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$

$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 +$

$+ a_5 * 194 + a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$

（此等式在Galois字段的操作中给出）
由于除零字节以外的所有内容都等于0，并且零字节乘以1，我们得到1，并将其写入数字的高位，将所有字节移至低位，则得到：

$C_1 = 00000000000000000000000000000001$

重复相同的操作。这次

$a_ {15} = 1$ ，所有其他字节均为0，因此，术语中仅第一个保留

$a_ {15} * 148 = 1 * 148 = 148_ {10} = 94_ {16}$ 我们得到：

$C_1 = 00000000000000000000000000000194$

我们进行第三次迭代，这是两个非零项：

$a_ {15} * 148 + a_ {14} * 32 = 148 * 148 + 1 * 32 =$

$= 10010100 * 10010100 + 00000001 * 00100000 =$

$=（x ^ 7 + x ^ 4 + x ^ 2）*（x ^ 7 + x ^ 4 + x ^ 2）+ 1 * x ^ 5 = x ^ {14} + x ^ 8 + x ^ 4 + x ^ 5 =$

$= x ^ 6（x ^ 8 + x ^ 7 + x ^ 6 + x +1）+ x ^ {13} + x ^ {12} + x ^ 7 + x ^ 6 + x ^ 8 + x ^ 4 + x ^ 5 =$

$= x ^ 5（x ^ 8 + x ^ 7 + x ^ 6 + x +1）+ x ^ {11} + x ^ 5 + x ^ 7 + x ^ 8 + x ^ 4 + x ^ 5 =$

$= x ^ 3（x ^ 8 + x ^ 7 + x ^ 6 + x +1）+ x ^ {10} + x ^ 9 + x ^ 3 + x ^ 8 + x ^ 7 =$

$= x ^ 2（x ^ 8 + x ^ 7 + x ^ 6 + x +1）+ x ^ 2 + x ^ 7 = x ^ 7 + x ^ 2 = 132_ {10}$

$132_ {10} = 84_ {16}$

根据度数表，可以轻松解决：

$148 * 148 + 1 * 32 = 2 ^ {45} * 2 ^ {45} + 2 ^ 5 = 2 ^ {90} + 2 ^ 5 = 164 + 32 = 132$

$C_1 = 00000000000000000000000000000000019484$

此外，一切都完全相同，每个常数只有16次迭代

$C_1 = 000000000000000000000000019484DD$

$C_1 = 0000000000000000000000019484DD10$

$C_1 = 00000000000000000000019484DD10BD$

$C_1 = 000000000000000000019484DD10BD27$

$C_1 = 0000000000000000019484DD10BD275D$

$C_1 = 00000000000000019484DD10BD275DB8$

$C_1 = 000000000000019484DD10BD275DB87A$

$C_1 = 0000000000019484DD10BD275DB87A48$

$C_1 = 00000000019484DD10BD275DB87A486C$

$C_1 = 000000019484DD10BD275DB87A486C72$

$C_1 = 0000019484DD10BD275DB87A486C727$

$C_1 = 00019484DD10BD275DB87A486C7276A2$

最后一个常量：

$C_1 = 019484DD10BD275DB87A486C7276A2E6$

其他常数：

$C_2 = 02EBCB7920B94EBAB3F490D8E4EC87DC$

$C_3 = 037F4FA4300469E70B8ED8B4969A25B2$

$C_4 = 041555F240B19CB7A52BE3730B1BCD7B$

$C_5 = 0581D12F500CBBEA1D51AB1F796D6F15$

$C_6 = 06FE9E8B6008D20D16DF73ABEFF74AA7$

$C_7 = 076A1A5670B5F550AEA53BC79D81E8C9$

$C_8 = 082AAA2780A1FBAD895605E6163659F6$

$C_9 = 09BE2EFA901CDCF0312C4D8A6440FB98$

$C_ {10} = 0AC1615EA018B5173AA2953EF2DADE2A$

$C_ {11} = 0B55E583B0A5924A82D8DD5280AC7C44$

$C_ {12} = 0C3FFFD5C010671A2C7DE6951D2D948D$

$C_ {13} = 0DAB7B08D0AD40479407AEF96F5B36E3$

$C_ {14} = 0ED434ACE0A929A09F89764DF9C11351$

$C_ {15} = 0F40B071F0140EFD27F33E218BB7B13F$

$C_ {16} = 1054974EC3813599D1AC0A0F2C6CB22F$

$C_ {17} = 11C01393D33C12C469D642635E1A1041$

$C_ {18} = 12BF5C37E3387B2362589AD7C88035F3$

$C_ {19} = 132BD8EAF3855C7EDA22D2BBBAF6979D$

$C_ {20} = 1441C2BC8330A92E7487E97C27777F54$

$C_ {21} = 15D54661938D8E73CCFDA1105501DD3A$

$C_ {22} = 16AA09C5A389E794C77379A4C39BF888$

$C_ {23} = 173E8D18B334C0C97F0931C8B1ED5AE6$

$C_ {24} = 187E3D694320CE3458FA0FE93A5AEBD9$

$C_ {25} = 19EAB9B4539DE969E0804785482C49B7$

$C_ {26} = 1A95F6106399808808EEB0E9F31DEB66C05$

$C_ {27} = 1B0172CD7324A7D35374D75DACC0CE6B$

$C_ {28} = 1C6B689B03915283FDD1EC9A314126A2$

$C_ {29} = 1DFFEC46132C75DE45ABA4F6433784CC$

$C_ {30} = 1E80A3E223281C394E257C42D5ADA17E$

$C_ {31} = 1F14273F33953B64F65F342EA7DB0310$

$C_ {32} = 20A8ED9C45C16AF1619B141E58D8A75E$

现在，我们将根据上述方案计算轮回密钥，并使用加密密钥：

$K = 7766554433221100FFEEDDCCBBAA9988$

$EFCDAB89674523011032547698BADCFE$

然后

$K_1 = 7766554433221100FFEEDDCCBBAA9988$

$K_2 = EFCDAB89674523011032547698BADCFE$

$K_1$ 将是Feistel网络的左侧子块，并且

$K_2$ -对
让我们做手术

$K_1 + C_1$
第一个字节

$K_1$ 等于

$77_ {16} = 01110111_2$
第一个字节

$C_1$ 等于

$01_ {16} = 00000001_2$

$01110111_2 + 00000001_2 = 01110110_2 = 76_ {16}$

结果，其余字节以相同的方式转换

$X（K_1，C_1）= K_1 + C_1$ ：

$X（K_1，C_1）= 76F2D199239F365D479495A0C9DC3BE6$

接下来，我们执行非线性变换

$S（X（K_1，C_1））$ 。它根据表执行：

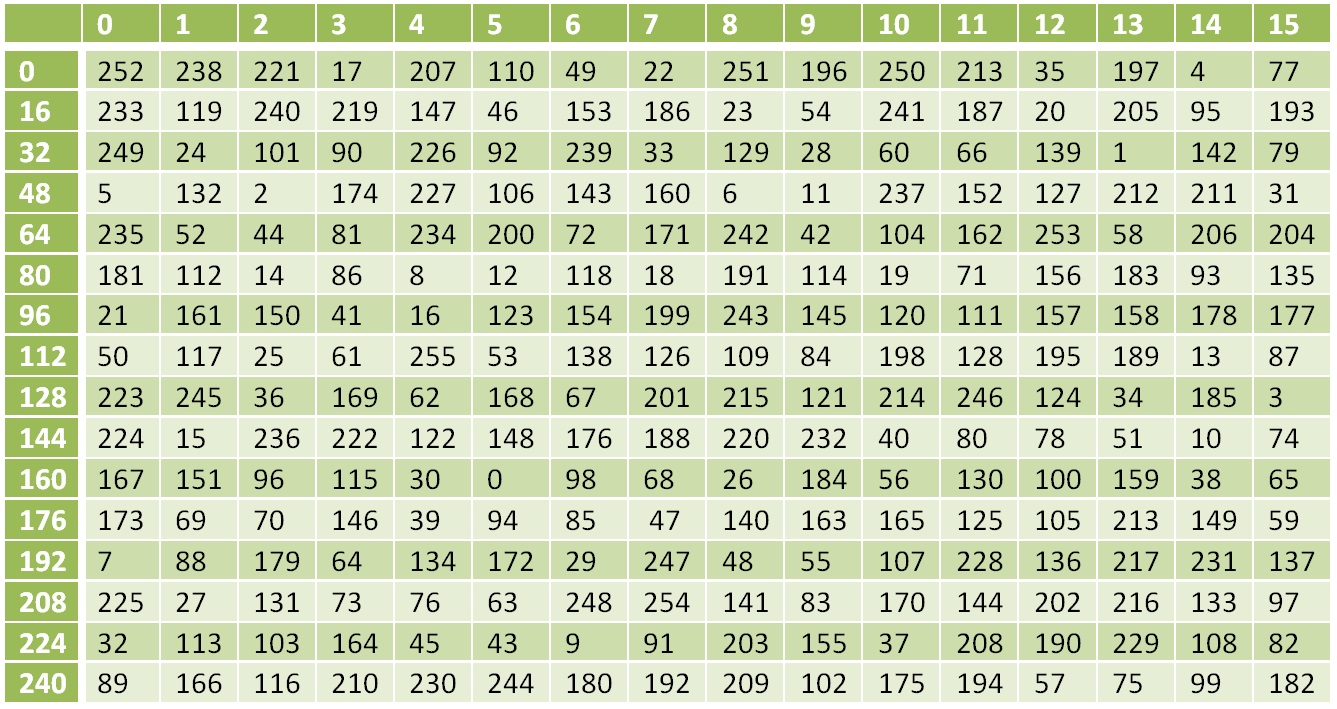非线性换算表

数字0替换为252、1替换为238、17替换为119等。

$76_ {16} = 118_ {10}$

$S（118）= 138_ {10} = 8A_ {16}$

$S（X（K_1，C_1））= 8A741BE85A4A8FB7AB7A94A737CA9809$

现在执行线性变换

$L（S（X（K_1，C_1）））$ ，在计算迭代常数时会对其进行详细考虑，因此在此我们仅给出最终结果：

$L（S（X（K_1，C_1）））= A644615E1D0757926A5DB79D9940093D$

根据Feistel单元的方案，我们对右侧的子块（即

$K_2$ ：

$X（L（S（X（X（K_1，C_1））），K_2）= 4989CAD77A4274937A6FE3EB01FAD5C3$

在第一个Feistel单元的输出处获得的结果是：

$EFCDAB89674523011032547698BADCFE4989CAD77A4274937A6FE3EB01FAD5C3$

此值减半，然后转到第二个Feistel单元格的输入，其中第二个常数已使用

$C_2$ 。经过八个单元格后，我们得到以下两个键

$K_3$ 和

$K_4$ 。我们将对它们执行Feistel网络的八次迭代，获取下一个密钥对，依此类推。每个键对八次迭代，因为我们最初有第一对，所以总共执行32次迭代，每个迭代都有自己的常数。

其余键：

$K_3 = 448CC78CEF6A8D2243436915534831DB$

$K_4 = 04FD9F0AC4ADEB1568ECCFE9D853453D$

$K_5 = ACF129F44692E5D3285E4AC468646457$

$K_6 = 1B58DA3428E832B532645C16359407BD$

$K_7 = B198005A26275770DE45877E7540E651$

$K_8 = 84F98622A2912AD73EDD9F7B0125795A$

$K_9 = 17E5B6CD732FF3A52331C77853E244BB$

$K_ {10} = 43404A8EA8BA5D755BF4BC1674DDE972$

块加密

我们计算了所有密钥，现在终于可以直接对文本块进行加密了，如果您仔细阅读了上面编写的所有内容，则对文本进行加密将不会很困难，因为已详细检查了此过程中使用的所有操作及其顺序。

取纯文本块：

$T = 8899AABBCCDDEEFF0077665544332211$

执行操作顺序X，S，L

$X（T，K_1）= FFFFFFFFFFFFFFFFFFFFFF99BB99FF99BB99$

$S（X（T，K_1））= B6B6B6B6B6B6B6B6B6E87DE8B6E87DE8$

$L（S（X（T，K_1）））= 30081449922F4ACFA1B055E386B697E2$

$T_1 = 30081449922F4ACFA1B055E386B697E2$

$X（T_1，K_2）= DFC5BFC0F56A69CEB18201951E0C4B1C$

$S（X（T_1，K_2））= 61AC3B07F47891E74524EE945F23A214$

$L（S（X（T_1，K_2）））= 7290C6A158426FB396D562087A495E28$

$T_2 = 7290C6A158426FB396D562087A495E28$

依此类推，最终结果将如下所示：

$T_ {10} = CDEDD4B9428D465A3024BCBE909D677F$

块解密

要解密文本，您需要以相反的顺序使用逆运算（请参见图2）。

XOR运算本身就是逆运算，而运算S的逆运算将根据下表进行替换：

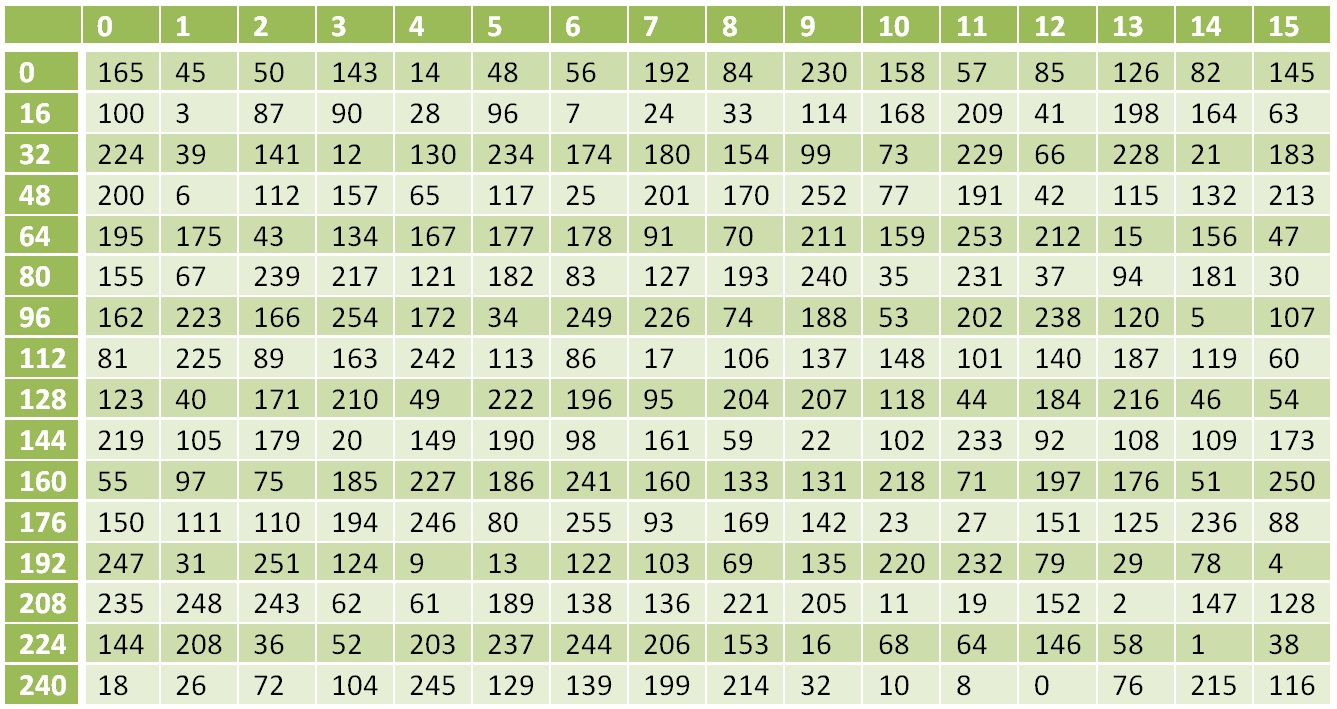逆非线性变换表

对函数L的逆变换将是：

$a_0 = a_ {15} * 148 + a_ {14} * 32 + a_ {13} * 133 + a_ {12} * 16 +$

$+ a_ {11} * 194 + a_ {10} * 192 + a_9 * 1 + a_8 * 251 + a_7 * 1 + a_6 * 192 + a_5 * 194 +$

$+ a_4 * 16 + a_3 * 133 + a_2 * 32 + a_1 * 148 + a_0 * 1$

并向高级方向转变。（重复操作16次）

Java实现

首先，我们定义必要的常数

static final int BLOCK_SIZE = 16; //   //     static final byte[] Pi = { (byte) 0xFC, (byte) 0xEE, (byte) 0xDD, 0x11, (byte) 0xCF, 0x6E, 0x31, 0x16, (byte) 0xFB, (byte) 0xC4, (byte) 0xFA, (byte) 0xDA, 0x23, (byte) 0xC5, 0x04, 0x4D, (byte) 0xE9, 0x77, (byte) 0xF0, (byte) 0xDB, (byte) 0x93, 0x2E, (byte) 0x99, (byte) 0xBA, 0x17, 0x36, (byte) 0xF1, (byte) 0xBB, 0x14, (byte) 0xCD, 0x5F, (byte) 0xC1, (byte) 0xF9, 0x18, 0x65, 0x5A, (byte) 0xE2, 0x5C, (byte) 0xEF, 0x21, (byte) 0x81, 0x1C, 0x3C, 0x42, (byte) 0x8B, 0x01, (byte) 0x8E, 0x4F, 0x05, (byte) 0x84, 0x02, (byte) 0xAE, (byte) 0xE3, 0x6A, (byte) 0x8F, (byte) 0xA0, 0x06, 0x0B, (byte) 0xED, (byte) 0x98, 0x7F, (byte) 0xD4, (byte) 0xD3, 0x1F, (byte) 0xEB, 0x34, 0x2C, 0x51, (byte) 0xEA, (byte) 0xC8, 0x48, (byte) 0xAB, (byte) 0xF2, 0x2A, 0x68, (byte) 0xA2, (byte) 0xFD, 0x3A, (byte) 0xCE, (byte) 0xCC, (byte) 0xB5, 0x70, 0x0E, 0x56, 0x08, 0x0C, 0x76, 0x12, (byte) 0xBF, 0x72, 0x13, 0x47, (byte) 0x9C, (byte) 0xB7, 0x5D, (byte) 0x87, 0x15, (byte) 0xA1, (byte) 0x96, 0x29, 0x10, 0x7B, (byte) 0x9A, (byte) 0xC7, (byte) 0xF3, (byte) 0x91, 0x78, 0x6F, (byte) 0x9D, (byte) 0x9E, (byte) 0xB2, (byte) 0xB1, 0x32, 0x75, 0x19, 0x3D, (byte) 0xFF, 0x35, (byte) 0x8A, 0x7E, 0x6D, 0x54, (byte) 0xC6, (byte) 0x80, (byte) 0xC3, (byte) 0xBD, 0x0D, 0x57, (byte) 0xDF, (byte) 0xF5, 0x24, (byte) 0xA9, 0x3E, (byte) 0xA8, (byte) 0x43, (byte) 0xC9, (byte) 0xD7, 0x79, (byte) 0xD6, (byte) 0xF6, 0x7C, 0x22, (byte) 0xB9, 0x03, (byte) 0xE0, 0x0F, (byte) 0xEC, (byte) 0xDE, 0x7A, (byte) 0x94, (byte) 0xB0, (byte) 0xBC, (byte) 0xDC, (byte) 0xE8, 0x28, 0x50, 0x4E, 0x33, 0x0A, 0x4A, (byte) 0xA7, (byte) 0x97, 0x60, 0x73, 0x1E, 0x00, 0x62, 0x44, 0x1A, (byte) 0xB8, 0x38, (byte) 0x82, 0x64, (byte) 0x9F, 0x26, 0x41, (byte) 0xAD, 0x45, 0x46, (byte) 0x92, 0x27, 0x5E, 0x55, 0x2F, (byte) 0x8C, (byte) 0xA3, (byte) 0xA5, 0x7D, 0x69, (byte) 0xD5, (byte) 0x95, 0x3B, 0x07, 0x58, (byte) 0xB3, 0x40, (byte) 0x86, (byte) 0xAC, 0x1D, (byte) 0xF7, 0x30, 0x37, 0x6B, (byte) 0xE4, (byte) 0x88, (byte) 0xD9, (byte) 0xE7, (byte) 0x89, (byte) 0xE1, 0x1B, (byte) 0x83, 0x49, 0x4C, 0x3F, (byte) 0xF8, (byte) 0xFE, (byte) 0x8D, 0x53, (byte) 0xAA, (byte) 0x90, (byte) 0xCA, (byte) 0xD8, (byte) 0x85, 0x61, 0x20, 0x71, 0x67, (byte) 0xA4, 0x2D, 0x2B, 0x09, 0x5B, (byte) 0xCB, (byte) 0x9B, 0x25, (byte) 0xD0, (byte) 0xBE, (byte) 0xE5, 0x6C, 0x52, 0x59, (byte) 0xA6, 0x74, (byte) 0xD2, (byte) 0xE6, (byte) 0xF4, (byte) 0xB4, (byte) 0xC0, (byte) 0xD1, 0x66, (byte) 0xAF, (byte) 0xC2, 0x39, 0x4B, 0x63, (byte) 0xB6 }; //     static final byte[] reverse_Pi = { (byte) 0xA5, 0x2D, 0x32, (byte) 0x8F, 0x0E, 0x30, 0x38, (byte) 0xC0, 0x54, (byte) 0xE6, (byte) 0x9E, 0x39, 0x55, 0x7E, 0x52, (byte) 0x91, 0x64, 0x03, 0x57, 0x5A, 0x1C, 0x60, 0x07, 0x18, 0x21, 0x72, (byte) 0xA8, (byte) 0xD1, 0x29, (byte) 0xC6, (byte) 0xA4, 0x3F, (byte) 0xE0, 0x27, (byte) 0x8D, 0x0C, (byte) 0x82, (byte) 0xEA, (byte) 0xAE, (byte) 0xB4, (byte) 0x9A, 0x63, 0x49, (byte) 0xE5, 0x42, (byte) 0xE4, 0x15, (byte) 0xB7, (byte) 0xC8, 0x06, 0x70, (byte) 0x9D, 0x41, 0x75, 0x19, (byte) 0xC9, (byte) 0xAA, (byte) 0xFC, 0x4D, (byte) 0xBF, 0x2A, 0x73, (byte) 0x84, (byte) 0xD5, (byte) 0xC3, (byte) 0xAF, 0x2B, (byte) 0x86, (byte) 0xA7, (byte) 0xB1, (byte) 0xB2, 0x5B, 0x46, (byte) 0xD3, (byte) 0x9F, (byte) 0xFD, (byte) 0xD4, 0x0F, (byte) 0x9C, 0x2F, (byte) 0x9B, 0x43, (byte) 0xEF, (byte) 0xD9, 0x79, (byte) 0xB6, 0x53, 0x7F, (byte) 0xC1, (byte) 0xF0, 0x23, (byte) 0xE7, 0x25, 0x5E, (byte) 0xB5, 0x1E, (byte) 0xA2, (byte) 0xDF, (byte) 0xA6, (byte) 0xFE, (byte) 0xAC, 0x22, (byte) 0xF9, (byte) 0xE2, 0x4A, (byte) 0xBC, 0x35, (byte) 0xCA, (byte) 0xEE, 0x78, 0x05, 0x6B, 0x51, (byte) 0xE1, 0x59, (byte) 0xA3, (byte) 0xF2, 0x71, 0x56, 0x11, 0x6A, (byte) 0x89, (byte) 0x94, 0x65, (byte) 0x8C, (byte) 0xBB, 0x77, 0x3C, 0x7B, 0x28, (byte) 0xAB, (byte) 0xD2, 0x31, (byte) 0xDE, (byte) 0xC4, 0x5F, (byte) 0xCC, (byte) 0xCF, 0x76, 0x2C, (byte) 0xB8, (byte) 0xD8, 0x2E, 0x36, (byte) 0xDB, 0x69, (byte) 0xB3, 0x14, (byte) 0x95, (byte) 0xBE, 0x62, (byte) 0xA1, 0x3B, 0x16, 0x66, (byte) 0xE9, 0x5C, 0x6C, 0x6D, (byte) 0xAD, 0x37, 0x61, 0x4B, (byte) 0xB9, (byte) 0xE3, (byte) 0xBA, (byte) 0xF1, (byte) 0xA0, (byte) 0x85, (byte) 0x83, (byte) 0xDA, 0x47, (byte) 0xC5, (byte) 0xB0, 0x33, (byte) 0xFA, (byte) 0x96, 0x6F, 0x6E, (byte) 0xC2, (byte) 0xF6, 0x50, (byte) 0xFF, 0x5D, (byte) 0xA9, (byte) 0x8E, 0x17, 0x1B, (byte) 0x97, 0x7D, (byte) 0xEC, 0x58, (byte) 0xF7, 0x1F, (byte) 0xFB, 0x7C, 0x09, 0x0D, 0x7A, 0x67, 0x45, (byte) 0x87, (byte) 0xDC, (byte) 0xE8, 0x4F, 0x1D, 0x4E, 0x04, (byte) 0xEB, (byte) 0xF8, (byte) 0xF3, 0x3E, 0x3D, (byte) 0xBD, (byte) 0x8A, (byte) 0x88, (byte) 0xDD, (byte) 0xCD, 0x0B, 0x13, (byte) 0x98, 0x02, (byte) 0x93, (byte) 0x80, (byte) 0x90, (byte) 0xD0, 0x24, 0x34, (byte) 0xCB, (byte) 0xED, (byte) 0xF4, (byte) 0xCE, (byte) 0x99, 0x10, 0x44, 0x40, (byte) 0x92, 0x3A, 0x01, 0x26, 0x12, 0x1A, 0x48, 0x68, (byte) 0xF5, (byte) 0x81, (byte) 0x8B, (byte) 0xC7, (byte) 0xD6, 0x20, 0x0A, 0x08, 0x00, 0x4C, (byte) 0xD7, 0x74 }; //    static final byte[] l_vec = { 1, (byte) 148, 32, (byte) 133, 16, (byte) 194, (byte) 192, 1, (byte) 251, 1, (byte) 192, (byte) 194, 16, (byte) 133, 32, (byte) 148 }; //     static byte[][] iter_C = new byte[32][16]; //     static byte[][] iter_key = new byte[10][64];

让我们创建所有主要功能：

 //  X static private byte[] GOST_Kuz_X(byte[] a, byte[] b) { int i; byte[] c = new byte[BLOCK_SIZE]; for (i = 0; i < BLOCK_SIZE; i++) c[i] = (byte) (a[i] ^ b[i]); return c; } //  S static private byte[] GOST_Kuz_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = Pi[data]; } return out_data; }

要实现函数L，我们需要几个辅助函数，一个用于计算Galois字段中数字的乘法，另一个用于移位。

 //     static private byte GOST_Kuz_GF_mul(byte a, byte b) { byte c = 0; byte hi_bit; int i; for (i = 0; i < 8; i++) { if ((b & 1) == 1) c ^= a; hi_bit = (byte) (a & 0x80); a <<= 1; if (hi_bit < 0) a ^= 0xc3; // x^8+x^7+x^6+x+1 b >>= 1; } return c; } //  R     ,    L- static private byte[] GOST_Kuz_R(byte[] state) { int i; byte a_15 = 0; byte[] internal = new byte[16]; for (i = 15; i >= 0; i--) { if(i == 0) internal[15] = state[i]; else internal[i - 1] = state[i]; a_15 ^= GOST_Kuz_GF_mul(state[i], l_vec[i]); } internal[15] = a_15; return internal; } static private byte[] GOST_Kuz_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal = in_data; for (i = 0; i < 16; i++) { internal = GOST_Kuz_R(internal); } out_data = internal; return out_data; }

反函数：

 //  S^(-1) static private byte[] GOST_Kuz_reverse_S(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; for (i = 0; i < BLOCK_SIZE; i++) { int data = in_data[i]; if(data < 0) { data = data + 256; } out_data[i] = reverse_Pi[data]; } return out_data; } static private byte[] GOST_Kuz_reverse_R(byte[] state) { int i; byte a_0; a_0 = state[15]; byte[] internal = new byte[16]; for (i = 1; i < 16; i++) { internal[i] = state[i - 1]; a_0 ^= GOST_Kuz_GF_mul(internal[i], l_vec[i]); } internal[0] = a_0; return internal; } static private byte[] GOST_Kuz_reverse_L(byte[] in_data) { int i; byte[] out_data = new byte[in_data.length]; byte[] internal; internal = in_data; for (i = 0; i < 16; i++) internal = GOST_Kuz_reverse_R(internal); out_data = internal; return out_data; } //    static private void GOST_Kuz_Get_C() { int i; byte[][] iter_num = new byte[32][16]; for (i = 0; i < 32; i++) { for(int j = 0; j < BLOCK_SIZE; j++) iter_num[i][j] = 0; iter_num[i][0] = (byte) (i+1); } for (i = 0; i < 32; i++) { iter_C[i] = GOST_Kuz_L(iter_num[i]); } } // ,     static private byte[][] GOST_Kuz_F(byte[] in_key_1, byte[] in_key_2, byte[] iter_const) { byte[] internal; byte[] out_key_2 = in_key_1; internal = GOST_Kuz_X(in_key_1, iter_const); internal = GOST_Kuz_S(internal); internal = GOST_Kuz_L(internal); byte[] out_key_1 = GOST_Kuz_X(internal, in_key_2); byte key[][] = new byte[2][]; key[0] = out_key_1; key[1] = out_key_2; return key; } //     public void GOST_Kuz_Expand_Key(byte[] key_1, byte[] key_2) { int i; byte[][] iter12 = new byte[2][]; byte[][] iter34 = new byte[2][]; GOST_Kuz_Get_C(); iter_key[0] = key_1; iter_key[1] = key_2; iter12[0] = key_1; iter12[1] = key_2; for (i = 0; i < 4; i++) { iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[0 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[1 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[2 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[3 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[4 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[5 + 8 * i]); iter34 = GOST_Kuz_F(iter12[0], iter12[1], iter_C[6 + 8 * i]); iter12 = GOST_Kuz_F(iter34[0], iter34[1], iter_C[7 + 8 * i]); iter_key[2 * i + 2] = iter12[0]; iter_key[2 * i + 3] = iter12[1]; } } //    public byte[] GOST_Kuz_Encript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; for(i = 0; i < 9; i++) { out_blk = GOST_Kuz_X(iter_key[i], out_blk); out_blk = GOST_Kuz_S(out_blk); out_blk = GOST_Kuz_L(out_blk); } out_blk = GOST_Kuz_X(out_blk, iter_key[9]); return out_blk; } //   public byte[] GOST_Kuz_Decript(byte[] blk) { int i; byte[] out_blk = new byte[BLOCK_SIZE]; out_blk = blk; out_blk = GOST_Kuz_X(out_blk, iter_key[9]); for(i = 8; i >= 0; i--) { out_blk = GOST_Kuz_reverse_L(out_blk); out_blk = GOST_Kuz_reverse_S(out_blk); out_blk = GOST_Kuz_X(iter_key[i], out_blk); } return out_blk; }

好了，主要功能

 static byte[] key_1 = {0x77, 0x66, 0x55, 0x44, 0x33, 0x22, 0x11, 0x00, (byte) 0xff, (byte) 0xee, (byte) 0xdd, (byte) 0xcc, (byte) 0xbb, (byte) 0xaa, (byte) 0x99, (byte) 0x88}; static byte[] key_2 = {(byte) 0xef, (byte) 0xcd, (byte) 0xab, (byte) 0x89, 0x67, 0x45, 0x23, 0x01, 0x10, 0x32, 0x54, 0x76, (byte) 0x98, (byte) 0xba, (byte) 0xdc, (byte) 0xfe}; static byte[] blk = DatatypeConverter.parseHexBinary("8899aabbccddeeff0077665544332211"); public static void main(String[] args) { GOST_Kuz_Expand_Key(key_1, key_2); byte[] encriptBlok = GOST_Kuz_Encript(blk); System.out.println(DatatypeConverter.printHexBinary(encriptBlok)); byte[] decriptBlok = GOST_Kuz_Decript(encriptBlok); System.out.println(DatatypeConverter.printHexBinary(decriptBlok)); }

我们学会了对数据块进行加密，以便对长度大于数据块长度的文本进行加密；标准-GOST 34.13-2015中描述了几种模式：

简单替换模式（电子密码书，ECB）；
伽玛模式（计数器，点击率）；
带输出反馈（输出反馈，OFB）的伽马模式；
简单的更换齿轮模式（Cipher Block Chaining，CBC）；
带有密文反馈的伽马模式（密码反馈，CFB）；
消息验证码（MAC）模式。

在所有模式下，文本长度应始终是块长度的倍数，因此，文本始终始终用一位填充到右边，而块的长度则填充为零。

最简单的模式是简单替换模式。在这种模式下，将文本分为多个块，然后将每个块与其余块分别加密，然后将密文的块粘合在一起，我们得到一个加密的消息。此模式既最简单又最易受攻击，几乎在实践中从未应用过。

其他模式可能会在后面详细介绍。

蚱hopper密码算法：复杂