大家好！ 我们为
“开发人员算法”课程推出了一套新课程，今天我们要分享为该课程的学生准备的有趣翻译。
在搜索树中，例如二进制搜索树，AVL树，红黑树等。 每个节点仅包含一个值（键），最多包含两个后代。 但是，有一种特殊的搜索树称为B树（发音为双树）。 在其中，该节点包含多个值（键）和两个以上的后代。 B树由拜耳（Bayer）和麦克莱思（McCraith）于1972年开发，被称为“
高度平衡m路搜索树” 。 它的现代名称B树后来被接受。
B树的定义如下：
B树是平衡的搜索树，其中的每个节点包含许多关键字，并具有两个以上的子节点。此处，节点中的键数及其后代数取决于B树的顺序。 每个B树都有一个顺序。
顺序为
m的 B树具有以下属性：
属性1：所有叶子的深度相同。
属性2：除根节点外的所有节点都必须至少具有
（m / 2）-1个密钥，最多
m-1个密钥。
属性3：除根节点外的所有无叶节点（即所有内部节点）必须至少具有
m / 2个后代。
属性4：如果根是无叶节点，则它必须至少具有
2个后代。
属性5：没有叶子且具有
n-1个键的节点必须具有
n个子节点。
属性6：节点中的所有键应按其值的升序排列。
例如，一个4阶B树包含每个节点最多3个键值和最多4个子级。
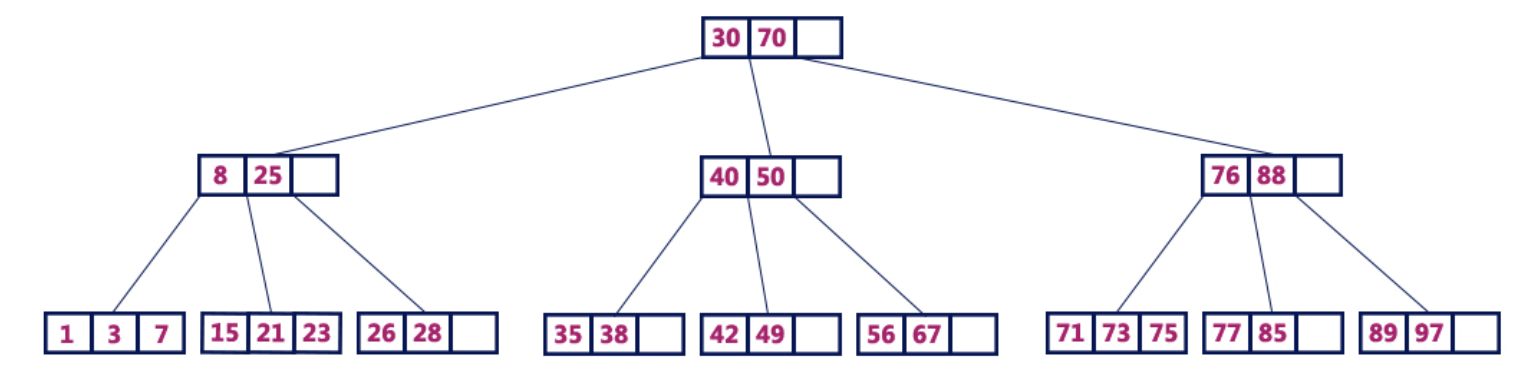B树4个订单B树操作可以在B树上执行以下操作：
- 搜寻
- 插入
- 删掉
搜索B树B树搜索类似于二叉树搜索。 在二叉搜索树中，搜索从根开始，并且每次做出双向决策时（沿着左侧子树或右侧）。 在B树中，搜索也从根节点开始，但是在每个步骤中都会做出n边决策，其中n是所讨论节点的后代总数。 在B树中，搜索复杂度为
O（log n） 。 搜索如下：
步骤1：阅读要搜索的项目。
步骤2：将搜索到的项目与树的根节点中的第一个键值进行比较。
步骤3：如果匹配，则打印：“找到节点！” 并完成搜索。
步骤4：如果不匹配，请检查项目值大于或小于当前键值。
步骤5：如果您要查找的项目较小，请继续搜索左侧子树。
步骤6：如果所需的项目较大，则将该项目与节点中的下一个键值进行比较，并重复步骤3、4、5和6，直到找到匹配项，或者直到将搜索到的项目与叶节点中的最后一个键值进行比较为止。
步骤7：如果列表节点中的最后一个键值与搜索不匹配，则打印“找不到项目！” 并完成搜索。
B树插入操作在B树中，只能将新项目添加到叶节点。 这意味着新的键值对始终仅添加到叶节点。 插入内容如下：
步骤1：检查树是否为空。
步骤2：如果树为空，请使用新的键值创建一个新节点，并将其作为根节点。
步骤3：如果树不为空，请使用二进制搜索树的逻辑找到合适的叶子节点，并将新值添加到该叶子节点。
步骤4：如果当前叶节点中有一个空单元格，请按照节点内键值的升序，向当前叶节点添加一个新的键值。
步骤5：如果当前节点已满并且没有空闲单元，则通过将平均值发送给父节点来拆分叶节点。 重复该步骤，直到将要发送的值提交到该节点。
步骤6：如果分离是与树的根发生的，则平均值将成为树的新根，并且树的高度将增加一。
一个例子：让我们通过添加1到10之间的数字来创建3阶的B树。
插入（1）：由于“ 1”是树的第一个元素，因此将其插入到新节点中，并且该节点成为树的根。
插入（2）：元素2已添加到现有叶节点。 现在我们只有一个节点，因此它同时是根和叶。 此工作表有一个空单元格。 然后“ 2”进入该空单元格。
插入（3）：元素3添加到现有叶节点。 现在我们只有一个节点，既是根节点又是叶节点。 此工作表没有空白单元格。 因此，我们通过将平均值（2）发送到父节点来分离该节点。 但是，当前节点没有父节点。 因此，平均值成为树的根节点。
插入（4）：元素“ 4”大于值为“ 2”的根节点，而根节点不是叶。 因此，我们沿着“ 2”的右子树移动。 我们来到值为“ 3”的叶节点，该节点具有一个空单元格。 因此，我们可以将“ 4”元素插入此空白单元格。
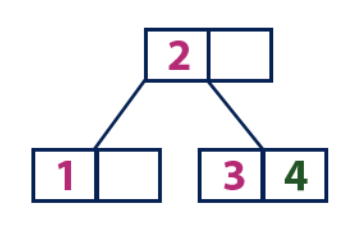插入（5）：元素“ 5”大于值为“ 2”的根节点，而根节点不是叶。 因此，我们沿着“ 2”的右子树移动。 我们来到叶节点，发现它已经满了并且没有空单元格。 然后，我们通过将平均值（4）发送到父节点（2）来划分该节点。 父节点为其具有一个空单元格，因此将值“ 4”添加到已经具有值“ 2”的节点上，并将新元素“ 5”作为新工作表添加。
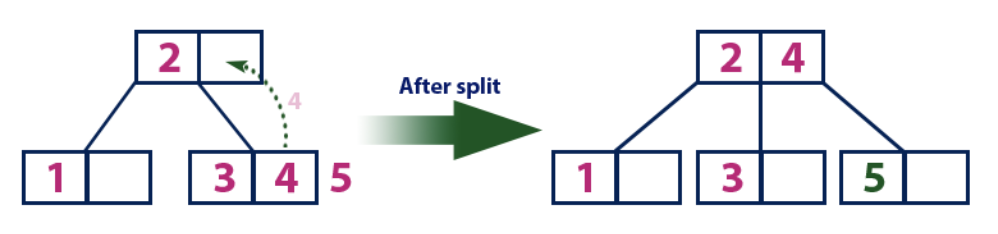插入（6）：元素“ 6”大于不是叶子的根“ 2”和“ 4”的元素。 我们沿着元素“ 4”的右子树移动。 我们到达值为“ 5”的工作表，该工作表具有一个空单元格，因此元素“ 6”正好放置在其中。
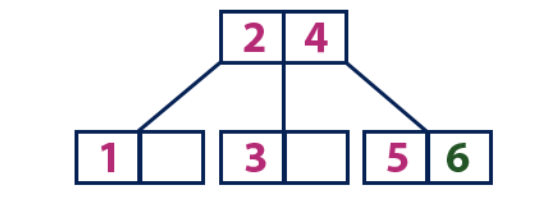插入（7）：元素“ 7”大于不是叶的根“ 2”和“ 4”的元素。 我们沿着元素“ 4”的右子树移动。 我们到达叶节点并看到它已满。 我们通过将平均值“ 6”发送到具有元素“ 2”和“ 4”的父节点来划分该节点。 但是，父节点也已满，因此我们将节点划分为元素“ 2”和“ 4”，将值“ 4”发送到父节点。 仅此节点尚不存在。 在这种情况下，具有元素“ 4”的节点将成为树的新根。
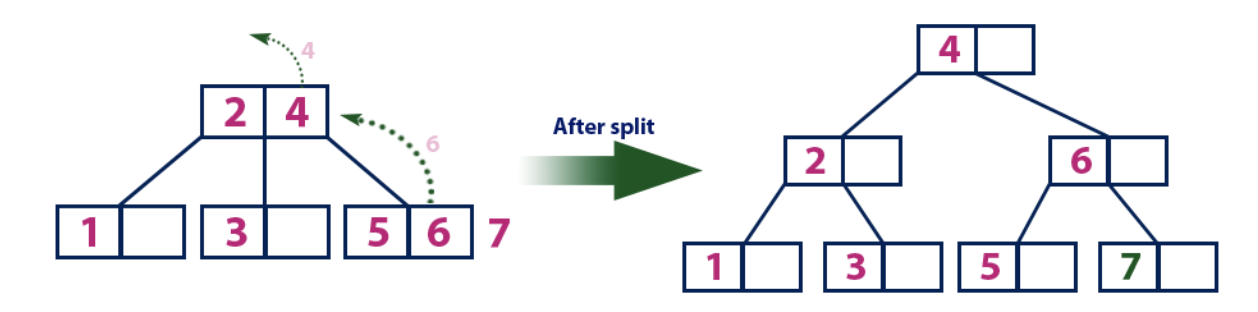插入（8）：元素8大于值为4的根节点，并且根节点不是叶。 我们从元素“ 4”沿右边的子树移动，并到达值为“ 6”的节点。 “ 8”大于“ 6”，并且元素为“ 6”的节点不是工作表，因此我们沿着“ 6”的右子树移动。 我们以“ 7”到达叶节点，该节点具有一个空单元格，因此我们将“ 8”放入其中。
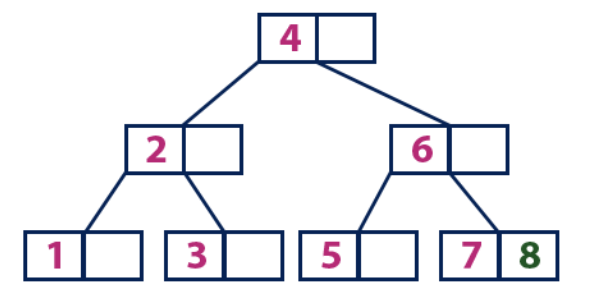插入（9）：元素9大于值为4的根节点，并且该根节点不是叶。 我们从元素“ 4”沿右边的子树移动，并到达值为“ 6”的节点。 “ 9”大于“ 6”，并且元素为“ 6”的节点不是工作表，因此我们沿着“ 6”的右子树移动。 我们到达叶节点的值为“ 7”和“ 8”。 他吃饱了。 我们通过将平均值（8）发送到父节点来划分该节点。 父节点“ 6”具有一个空单元格，因此我们将“ 8”放入其中。 在这种情况下，新元素“ 9”被添加到节点列表中。
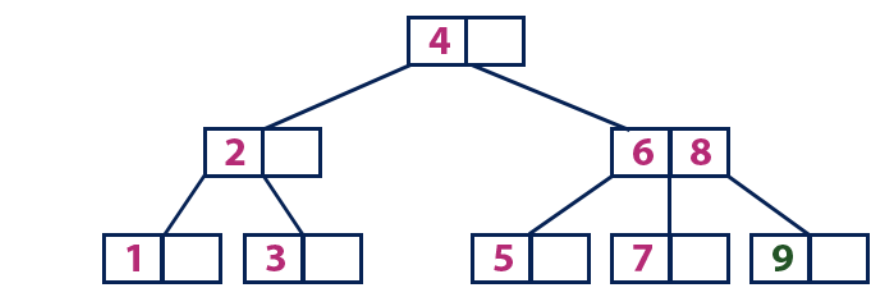
插入（10）：
元素“ 10”大于值为“ 4”的根节点，而根节点不是叶子。 我们从元素“ 4”沿右边的子树移动，并到达值“ 6”和“ 8”的节点。 “ 10”大于“ 6”和“ 8”，并且具有这些元素的节点不是工作表，因此我们沿着“ 8”的右子树移动。 我们到达叶节点的值为“ 9”。 他有一个空单元格，因此我们在其中放置了“ 10”。
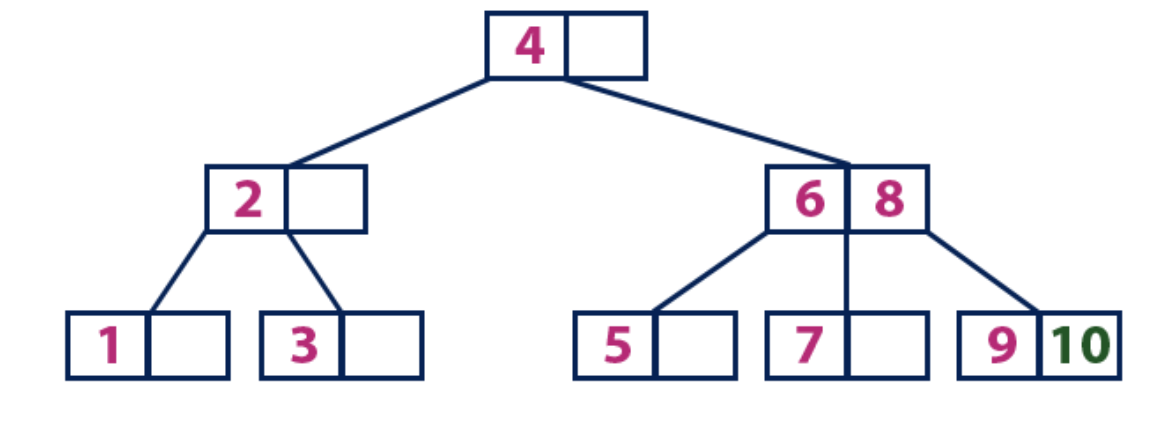
我们建议您在实践中独立地理解使用
此可视化文件如何排列B树。
我们正在等待所有人参加将于7月12日举行的
免费公开课 。 待会见！