在这项工作中，保留了基本的
G 2±模型，但是接受了其细胞的不同组织（另一个图）。 在具有
1×1像元的主晶格的顶部，代表了一个较大的网格-菱形网格，并且还考虑了菱形中心网格（SCR）。 未描绘最后一个网格，以免菱形图案使线条过载。 我们将不再重复
先前 作品中详细描述的定义和概念，而是提供指向这些作品的链接。
建设性模型说明
通过在
G 2--子模型中偶数长
D i和短
K i对角线中包含的单元格
G 2± -模型（其数字以零结尾），绘制了在平面上形成大型菱形网络的线。 细胞的菱形区域共同覆盖整个平面而没有间隙。 每个菱形都包含41个单元格，其中只有16个是感兴趣的，并且在探测菱形时，仅使用4个具有固定屈曲的单元格。
菱形的特征将包括：
- 菱形中的细胞数量；
- 中央单元格中数字的值；
- 其水平数（ N i ）和垂直数（ V i ）的数目；
- 识别具有1、3、7、9变形的数字的单元格；
- 这些单元格在菱形坐标系中的坐标，其原点在菱形中心单元中。
还通过菱形中心的单元构建菱形中心的网格，菱形中心的节点位于长对角线和短对角线相交处的单元中，该对角线的数量是数字5的倍数。
从带有菱形的图中，可以清楚地看到涉及哪种网格。 为了说明菱形的特征，给出了每个半平面中一对菱形的图像。 这些菱形在下半部分标记有识别的细胞数量，在上半平面中标记有另一对这样的菱形。 在对角线
D 0下方的半平面中的菱形标记不同于在对角线
D 0上方的半平面中的菱形标记，但是在同一半平面内，上下半平面的所有菱形标记均相同。 标记的本质是对具有相同拐点的数字的单元格进行定位（通过用相同的颜色填充单元格来标记），并设置其坐标
x 1 ，
x 0 。 指定的菱形将被称为基本菱形；可以从中形成其他具有放大功能的菱形。
下半平面菱形的中心是数字以两位数结尾的单元格，其中水平数字25的屈曲度为5，垂直数字的屈度为0，或75水平数字的屈曲度为0，垂直数字为屈度为5。在上半平面
2 + -子模型，所有菱形中心单元中的所有数字以两位数25结尾。此外，我们将考虑范围限制在半平面
2-上 。
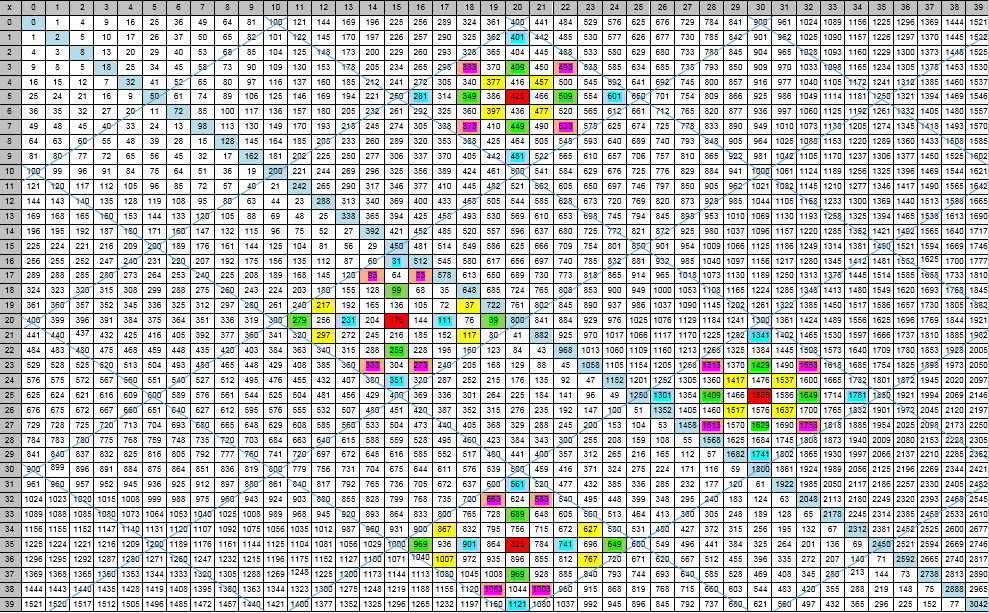图1-钻石模型的可视化表示定义1.基本菱形是
2 ± -模型的结构，受到该平面的两个短和两个长对角线的限制，其对角线的数字是数字10的倍数。表征菱形的主要元素是其中心的像元（
x 1c ，
x 0c ）。 中心包含N的数值，是5的倍数。
定义2.基本菱形中心的集合是交叉的短对角线和长对角线（数为5的倍数）的菱形中心（SCR）网络的节点（单元）。菱形本身完全覆盖了平面
2 ± -模型（镶木地板原理）。
所有菱形都以相同的方式排列，并且其单元格中具有固定结尾的数字被放置在固定位置（单元格）。 当解决在特定菱形中定位数字
N的问题时，这使您可以轻松分解该数字。 十个水平单元的单元格形成菱形，相邻的菱形（坐标不同）将被称为一条菱形带。 考虑水平带：西-东（）； 垂直：南北（NW），短对角线：东北（NE），长对角线：西北（NW）。 从一个菱形到另一个菱形的偏移，除了可以指示条带外，还可以沿着指示的频段附加一个指示（上下）。
由于根据定义2得出所有菱形的单元格集合都是
G 2±模型的所有单元格，因此在属于某个菱形的一个单元格
（x 1p ，x 0p ）中 ，给定的复合奇数自然数（ELF）
N（ x 1p ，x 0p ）= N（x 1 ，x 0 ） 。 同时，我们认为可以指示这种菱形（通过确定其中心单元的坐标）
（x 1c ，x 0c ），而不是探测所有单元，甚至将自身限制为仅探测奇数对角线。
对于给定的数
N（x 1 ，x 0 ），指示这种菱形和其中的所需单元格是解决定位问题的方法。 该问题及其解决方案是在收到WFCH的决定之前进行的。 定位问题的含义和最终目的是在给定的ELF
N（x 1 ，x 0 ）的特定菱形中指示
G 2±模型中单元格
（x 1p ，x 0p ）的坐标值，其中存在一个与
N一致的数字
（x 1 ，x 0 ） 。
在本文中，我们使用一种机制来建立给定数N到特定菱形和其中一个单元的归属。 这种机制远非最佳，但是在提出的示例中，它可以解决这一任务。 欢迎读者提供其原创作品，或改进此机制。
我们的机制基于作者发现的
G 2±模型的显着规律性：水平线中存在数为5（及其他一些数）的倍数的细胞，勾股勾股三元组（PFT）的元素的平方<
g，k 1 ，k 2 > = <斜边，腿
1 ，腿
2 >。 CFT将在另一篇工作中讨论。
为了简化结论和计算，我们需要三个坐标系：
已引入的平面坐标系，用于SCR的其他对角线网络（图2）和菱形（表1），其中起点与菱形中心的单元格相关。
图2.短对角线和
短对角线上的钻石中心分布表1.确定固定菱形内搜索点的坐标
在SCR系统中，指示以下内容：短对角线
n p ，
c是其上中心的序列号，以及全网
C中心号，它们自己的短对角线编号从
n p = 1开始 （在平面系统中为第五个短对角线） ，则数字
n p = 2（这是数字增加10，即第15平面
K i ），然后是第10步，其他所有数字。
在 SCR的每个
K i中，菱形中心的所有单元的位置也从短对角线
的双网络数的
c = 1到
c = 2n p进行编号。
例子1 让我们需要找到一个菱形中心的全网编号
C和该单元格中对于穿过菱形中心的给定短对角线的数字N，其网络编号
n p = 5和其中一个菱形的中心
c = 3的序列号。 非常简单地，该菱形中心单元的网络坐标以
（n p ，q）=（5，3）的形式表示。
- 在给定对角线（nd）的开头找到像元的平面x 1坐标：
x 1 = x nd = 10n p -5 = 50-5 = 45。
对于我们的情况，我们得到x 1 = x nd = 45 。
- 现在我们可以立即开始搜索所需中心的像元（ x 1c ， x sc ）的平面坐标： x 1 = x nd -5（c-1）= 45-5（3-1）= 35，x 0 = 0 + 5（ μ-1）= 2∙5 = 10。
- 找出菱形中心的网络编号（ C ）。
备注。 已知对于数字x，公式2C x + 1 2 = x（x + 1）是x +1的组合在两个中的两倍。
短对角线n p = 5之前的中心数量为2n p （n p -1） 。 然后，网络中心的序列号C由以下公式给出
C = n p （n p -1）+ c = 2C n p 2 + 3 = 5∙4 + 3 = 23 。
- 在菱形中心的单元格中找到数字N（x 1c ，x sc ）的值N = x 1 2 -x 0 2-公式中的符号取决于中心相对于主对角线的位置。
对于我们的情况， N = 35 2-10 2 = 1125 。
因此，仅使短对角线的网络编号
n p穿过中心的像元，并且使菱形
c的当前中心编号在该对角线上，我们就可以获得有关菱形中心的所有其他信息。
所有感兴趣的奇数正整数
N都属于菱形单元。 屈曲的概念是数字的最后一位，它可以在菱形内定位其位置。 对于因式分解，以数字
1、3、7、9结尾的数字
N是有意义的。
偶数不被视为
N ，因为它们有一个质数除数2。以5结尾的数字具有质数除数5，这对于
N也是不可接受的
。 在中心是菱形最重要的事实的情况下，建议通过在菱形内相对于菱形中心的变形来定位特定的
N。 基于所有菱形都具有相同结构的事实，为分解指定的数字
N与具有一定弯曲度的菱形单元中和菱形中心单元中的数字之间存在明确的关系。 表中给出了有关这种关系编号的数据。 1。
然而，在时间上或计算成本上，将平面上的所有菱形整理出来以找到所需的菱形都是不可接受的。 因此，出现了定位区域
2-子模型（半平面）的问题，其中包括将包含要分解的初始数
N的菱形。
毕达哥拉斯三联 。 解决所提出的问题
毕达哥拉斯三元组是满足毕达哥拉斯定理的数字的三元组：即毕达哥拉斯三元组满足所谓的埃及三角形的规则，即边长为3、4、5的倍数的三角形。
在每个包含菱形中心的水平
x 1中，有一个或多个这样的毕达哥拉斯三元组。
定位问题中的第一个菱形被近似表示，如果出现“缺失”，则应选择以下菱形。 为此，有必要确定沿着SCR的运动方向，以便逐渐接近最终目标。 例如，如果当前菱形中4个中的较小者小于给定的N，则东北菱形和东部菱形中的数量甚至少于4个，也就是说，不应探测此类菱形。 迁移到西方菱形会导致其所有4个单元的值增加，以至于即使是数量较少的西方菱形也比以前的较大数量的菱形更大，因此也大于N.
如果找到包含数量等于
N（x 1p ，x 0p ） =
N的像元的菱形并且确定了像元
（x 1p ，x 0p ）的坐标，则FBCH的解由模型的基本关系2
± -确定
N = x 2 1 -x 2 0 =（x 1 -x 0 ）（x 1 + x 0 ）= p∙q另一个子问题是菱形的用于探测的细胞旁路序列的选择和实现。 在这里，采用逆时针遍历顺序，从左上角的单元格开始，该单元格包含具有所需拐点的数字。 在菱形单元
N（x 1p ，x 0p ）和给定数N（x 1 ，x 0 ）中值相符的情况下，它们之间
的差变为零。
使用基本菱形和PFT的ZFBCH解决算法- 我们从数字N中提取根。 四舍五入。
- 我们检查√N是否可被3 整除 。如果可整 ，则将此值分配给第一个分支k1，否则， 要用 3满足可除性，请从结果中减去1或2，然后将其作为k1输入到内存中。 将完全选择的值除以三个M =√N/ 3的结果 -请记住缩放PFT系数。
- 根据埃及三角的规则，我们得到第二条腿的值k 2 ， k 2 = 4∙M。
- 我们找到了斜边的值g = 5∙M ，并且值x 1 = g应该除以数字5。 如您所见，斜边的值始终等于使用PFT的水平数。
- 找出坐标x 1 = g 。
- 之后，我们确定数字N的变形（最后一位）， φ= N（mod10） 。
- 我们找到最接近k1的菱形中心，然后检查菱形带之一（有4个方向）中的相邻菱形以找到解决方案。
- 根据我们在第6段中得到的变化，我们使用表中列出的所需列（掩码）。 1确定搜索点的坐标（ x 1p ， x 0p ）并在该单元格N p中找到该数字的值。 在每个菱形中，从第41个单元格只检查了4个单元格。
- 在确定数字N属于特定菱形和其中的一个单元之后，基于同一表格。 1我们得到平面坐标N：（x 1p ，x 0p ） 。
- 使用所选数学模型的属性
N = x 2 1 -x 2 0 =（x 1 -x 0 ）（x 1 + x 0 ）= p∙q
我们从加法器中获得N的乘法表示。
- 因此，在算法的输出处，我们有： N = p∙q 。 根据表中的公式取决于屈曲f的值。 如图1所示，确定点（x 1p ，x 0p ）的坐标， 并计算出差 Δ＝ N（x 1p ，x 0p ）-N（x 1 ，x 0 ） 。 如果∆≠0 ，则转到另一个单元格，如果检查了菱形的所有单元格，则转到另一个菱形。
如果Δ= 0 ，则x 1 = x 1p ，x 0 = x 0p和p =（x 1 -x 0 ） ， q = N / p =（x 1 + x 0 ） 。
示例2.给定：
N = 1037 ，一个容量为4的数字。需要将其分解。 我们根据给定的算法进行操作。
- 我们从N提取根： √N= 32.202 。 我们舍入： √N= 32 。
- 我们检查32是否可被3整除。由于32无法被3整除，因此我们减去2。因此，我们假设第一条边为k 1 = 3∙10 = 30 ，这里M = 10 = 30/3是PFT比例因子。
- 我们得到第二条腿的值k 2 = 4∙10 = 40 。
- 我们找到斜边值g =（k 2 1 + k 2 2 ） 0.5 ，条件是将它除以5 （30 2 +40 2 ） 0.5 = 50。
- 因此，x1 = k1 = 50，PFT转换为g = 50 ， k 1 = 30，k 2 = 40的形式 。
- 我们发现数字N的变形： φ（1037）= 1037（mod10）= 7 。
- 我们发现菱形的中心最接近N = 1037 。
它具有菱形中心细胞的坐标： x 1 = 50，x 0 = 35 。 第一个坐标是包含CFT的行号。 小腿的平方为900，它包含在垂直数为40的单元格中。数字957以七个最接近900的单元格结尾的单元格位于前一个水平数为49的单元格中，而垂直数为38的单元格。这是菱形中最小的4拐点7.这里我们使用表1的数据。菱形的最近中心应位于左侧三个像元，即它属于垂直38-3 = 35，这是菱形中心的第二个坐标。 菱形中心的像元中的数字值为N（ 50，35 ）= 1275
这是一个菱形，在其边界处具有腿k 1和k 2的平方。 在这个菱形中，min是一个以七个957结尾的数字，位于一个像元中（ x 1 = 49，x 0 = 38 ），而另一个垂直于此数字的结尾为7th 1157 ，则大数字1377和1577位于中心像元的左侧，与该数字一致N = 1037否，因此，有必要使用中心单元格1125中的值和中心单元格的坐标（左侧x 1 = 50-5 = 45，x 0 = 35-5 = 30 ）向左或向上方升高菱形，检查屈曲度的四个数字7它们分别是847、1027、1207和1387，在这个菱形中没有N = 1037的巧合），我们将沿着菱形的NW波段朝同一方向上升甚至更高。 新菱形的像元中心具有975的值和坐标（ x 1 = 45 -5 = 40，x 0 = 35-5 = 25 ）。 我们在菱形中检查拐点7的四个数字。这是737、897、1197 ，最后在单元格中得到1037 （ x 1p = 39，x 0p = 22 ），我们得到与给定N的完全匹配。
详细地，这些动作由以下计算表示：根据表1，我们计算单元格的坐标及其中的数值。 之后，我们发现计算出的值和给定的N值之间的差异。在第一个菱形中，计算了所有4个像元。
∆ = N（x 1c -1，x 0c -3）-N（x 1 ，x 0 ） = N（49.32）-1037 = 1377-1037 = 340≠0，
∆ = N（x 1c +1，x 0c -3）-N（x 1 ，x 0 ） = N（51.32）-1037 = 1577-1037 = 540≠0，
∆ = N（x 1c +1，x 0c +3）-N（x 1 ，x 0 ） = N（51.38）-1037 = 1157-1037 = 120≠0，
∆ = N（x 1c -1，x 0c +3）-N（x 1 ，x 0 ） = N（49.38）-1037 = 957-1037 =-80≠0。
在此菱形中，数字N与单元格中的数字不重合。
我们转到下一个菱形，其中单元格的中心（x 1c -5，x 0c -5）=（ 45，30 ） ，其中的值N（x 1c -5，x 0c -5）= N（ 45，30 ）= 1125 。
∆ = N（x 1ts -1，x 0ts -3）-N（x 1 ，x 0 ） = N（44.27） -1037 = 1207-1037 = 170≠0，
∆ = N（x 1c +1，x 0c -3）-N（x 1 ，x 0 ） = N（46.27）-1037 = 1387-1037 = 350≠0，
∆ = N（x 1c +1，x 0c +3）-N（x 1 ，x 0 ） = N（46.33）-1037 = 1027-1037 =-10≠0，
∆ = N（x 1c -1，x 0c +3）-N（x 1 ，x 0 ） = N（44.33）-1037 = 847-1037 =-190≠0。
在这个菱形中，数字N和单元格中的数字也不重合。
我们转到下一个菱形，其中单元格的中心（x 1c -5，x 0c -5）=（ 40，25 ） ，其中的值N（x 1c -5，x 0c -5）= N（ 40，25 ）= 975
∆ = N（x 1c -1，x 0c -3）-N（x 1 ，x 0 ） = N（39.22）-1037 = 1037-1037 = 0。
值的差为零。 完全是巧合。 由此可以得出，给定数字N（x 1 ，x 0 ）= 1037包含在坐标为（ x1 ， x0 ）=（ 39，22 ）的像元中。最后，HFBC的解是由模型的基本关系2 ± -确定的
N = x 2 1 -x 2 0 =（x 1 -x 0 ）（x 1 + x 0 ）=（39-22）（39 + 22）= p∙q = 17∙61 。
- 您可以采取不同的行动，从第6段中所示的菱形开始，使用表格。 如图1所示，我们找出数字N是否属于特定的菱形，首先在菱形的中心之间水平移动，朝主对角线移动，然后向下移动到下一个菱形带，然后再次重复所有操作。
- 在确定数字N属于某个菱形之后（在我们的示例中，菱形将具有基于同一表格的坐标（ x 1 = 40，x 0 = 25 ））。 1得到坐标N ： x 1p = 39 ， x 2p = 22 （查看9个菱形）。
- 使用选定数字的数学模型的属性
N = x 2 1 -x 2 0 =（x 1 -x 0 ）（x 1 + x 0 ）= p∙q
我们从加法器中得到N的乘法表示：
N =（39-22）（39 + 22）= 17∙61 = 1037 。
因此，在输出处，我们有
N = p·q = 17·61 = 1037 ，即，成功地解决了问题。
在示例3中，我们还获得了针对该问题的软件解决方案的结果。
例子3 给定：N = 3808572773，分辨率为10的数字。
- 我们从N提取根：√N= 61713，64 = 61713 。
- 检查61713是否可被3整除。由于61713可被3整除，因此，
6 +1 + 7 +1 + 3 = 18除以3，则第一条腿k 1等于k 1 = 61713 。 - 我们得到第二条腿k 2 = 4k 1/3 => 4k 2/3 = 82284 。
- 我们找到斜边g =√k12 + k 22 ，只要将其除以
5克=√617132+ 822842 = 102855 。 - 因此， x 1 = k 1 = 61713 ，勾股三重变换分别为形式k 1 = 61713，k 2 = 82284，g = 102855 。
- N: (3808572773) = 3808572773(mod10) = 3 .
- . x 1 = 61715; x 9 = 0 .
- , 7, . 1, N , , , , .
- N ( x 1 = 62015 , x 0 = 6085 ) N :
x 1p = 62013; x 0p = 6086 ; ( 60 ).
N = x 2 1 — x 2 0 = (x 1 — x 0 )(x 1 + x 0 ) =p ·q N :
N = (62013 — 6086) · (62013 + 62086) = 55927 · 68099 = 3808572773 ;- , N = p · q = 55927 · 68099 = 3808572773 , . . .