想象一下，您需要生成一个从1到10的均匀分布的随机数。即，一个从1到10的整数（含1和10），并且每次出现的概率均等（10％）。但是，也就是说，无法访问硬币，计算机，放射性物质或其他（伪）随机数的类似来源。您只能与人同住一个房间。

假设这个房间里有8500多名学生。

最简单的事情是问一个人：“嘿，从1到10中选择一个随机数！”。那人回答：“七个！”。太好了！现在您有一个电话号码。但是，您开始怀疑它是否均匀分布。

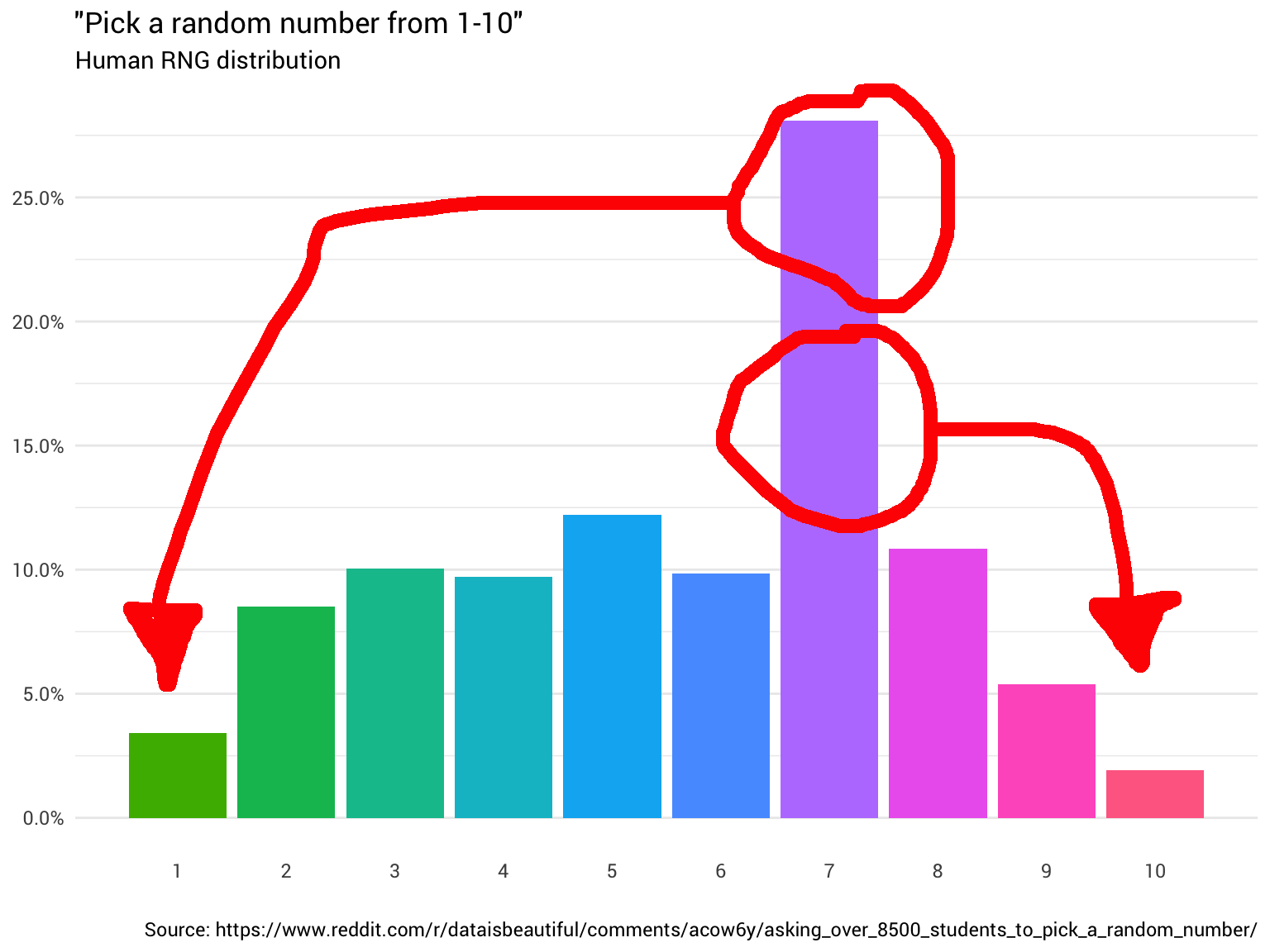
所以您决定再问几个人。您不断询问他们并计算他们的答案，四舍五入小数，而忽略那些认为从1到10的范围包括0的人。最后，您开始发现分布根本不均匀：

library(tidyverse) probabilities <- read_csv("https://git.io/fjoZ2") %>% count(outcome = round(pick_a_random_number_from_1_10)) %>% filter(!is.na(outcome), outcome != 0) %>% mutate(p = n / sum(n)) probabilities %>% ggplot(aes(x = outcome, y = p)) + geom_col(aes(fill = as.factor(outcome))) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = '"Pick a random number from 1-10"', subtitle = "Human RNG distribution", x = "", y = NULL, caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/")

来自Reddit的数据

你拍你的额头。好吧，当然，它不会是随机的。毕竟，你不能信任别人。

那该怎么办呢？

我希望我能找到一些功能来将“人类RNG”的分布转换为统一的分布...

直觉在这里相对简单。您只需要从大于10％的位置获取分配质量，然后将其移动到小于10％的位置即可。这样图表上的所有列都处于同一级别：

理论上，这种功能应该存在。实际上，必须有许多不同的功能（用于排列）。在极端情况下，您可以将每列“切割”成无限小的块，并构建任何形状的分布（例如Lego积木）。

当然，这样一个极端的例子有点麻烦。理想情况下，我们希望保留尽可能多的初始分布（即，尽可能减少碎片和移动）。

如何找到这样的功能？

好吧，我们上面的解释听起来很像线性编程。从维基百科：

线性规划（LP，也称为线性优化）是一种在数学模型中以线性关系表示其要求的方法，以获得最佳结果。标准形式是描述线性规划问题的通常且最直观的形式。它包括三个部分：

线性函数要最大化
以下形式的问题局限性
非负变量

同样，可以提出重新分配的问题。

问题介绍

我们有一组变量

（ x_{i ， j}

$（x_ {i，j}$ ，每个都编码从整数重新分配的几分之一概率

我

$我$ （1到10）为整数

j

$j$ （从1到10）。因此，如果

（ x_{7, 1} = 0.2

$（x_ {7,1} = 0.2$ ，那么我们需要将答案的20％从7转移到1。

 variables <- crossing(from = probabilities$outcome, to = probabilities$outcome) %>% mutate(name = glue::glue("x({from},{to})"), ix = row_number()) variables

  ##＃小标题：100 x 4
 ##从到名称ix
 ## <dbl> <dbl> <胶水> <int>
 ## 1 1 1 x（1,1）1
 ## 2 1 2 x（1,2）2
 ## 3 1 3 x（1,3）3
 ## 4 1 4 x（1,4）4
 ## 5 1 5 x（1,5）5
 ## 6 1 6 x（1,6）6
 ## 7 1 7 x（1,7）7
 ## 8 1 8 x（1,8）8
 ## 9 1 9 x（1.9）9
 ## 10 1 10 x（1,10）10
 ##＃...还有90多行

我们希望限制这些变量，以便所有重新分配的概率加起来为10％。换句话说，对于每个

j

$j$ 从1到10：

x_{1 ， j} + x_{2 ， j} + l d o t s x_{10 ， j} = 0.1

$x_ {1，j} + x_ {2，j} + \ ldots \ x_ {10，j} = 0.1$

我们可以将这些限制表示为R中的数组列表。稍后，我们将它们绑定到矩阵中。

 fill_array <- function(indices, weights, dimensions = c(1, max(variables$ix))) { init <- array(0, dim = dimensions) if (length(weights) == 1) { weights <- rep_len(1, length(indices)) } reduce2(indices, weights, function(a, i, v) { a[1, i] <- v a }, .init = init) } constrain_uniform_output <- probabilities %>% pmap(function(outcome, p, ...) { x <- variables %>% filter(to == outcome) %>% left_join(probabilities, by = c("from" = "outcome")) fill_array(x$ix, x$p) })

我们还必须确保保留初始分布中的全部概率。所以对大家

j

$j$ 范围从1到10：

x_{1 ， j} + x_{2 ， j} + l d o t s x_{10 ， j} = 0.1

$x_ {1，j} + x_ {2，j} + \ ldots \ x_ {10，j} = 0.1$

 one_hot <- partial(fill_array, weights = 1) constrain_original_conserved <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome) %>% pull(ix) %>% one_hot() })

如前所述，我们希望最大程度地保留原始发行版。这是我们的目标：

最 大 化 （ x_{1 ， 1} + x_{2 ， 2} + l d o t s x_{10 ， 10} ）

$最大化（x_ {1，1} + x_ {2，2} + \ ldots \ x_ {10，10}）$

 maximise_original_distribution_reuse <- probabilities %>% pmap(function(outcome, p, ...) { variables %>% filter(from == outcome, to == outcome) %>% pull(ix) %>% one_hot() }) objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums()

然后，我们将问题传递给求解器，例如R中的lpSolve包，将创建的约束组合到一个矩阵中：

 # Make results reproducible... set.seed(23756434) solved <- lpSolve::lp( direction = "max", objective.in = objective, const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)), const.dir = c(rep_len("==", length(constrain_original_conserved)), rep_len("==", length(constrain_uniform_output))), const.rhs = c(rep_len(1, length(constrain_original_conserved)), rep_len(1 / nrow(probabilities), length(constrain_uniform_output))) ) balanced_probabilities <- variables %>% mutate(p = solved$solution) %>% left_join(probabilities, by = c("from" = "outcome"), suffix = c("_redistributed", "_original"))

返回以下重新分配：

 library(gganimate) redistribute_anim <- bind_rows(balanced_probabilities %>% mutate(key = from, state = "Before"), balanced_probabilities %>% mutate(key = to, state = "After")) %>% ggplot(aes(x = key, y = p_redistributed * p_original)) + geom_col(aes(fill = as.factor(from)), position = position_stack()) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(labels = scales::percent_format(), breaks = seq(0, 1, 0.05)) + scale_fill_discrete(h = c(120, 360)) + theme_minimal(base_family = "Roboto") + theme(legend.position = "none", panel.grid.major.x = element_blank(), panel.grid.minor.x = element_blank()) + labs(title = 'Balancing the "Human RNG distribution"', subtitle = "{closest_state}", x = "", y = NULL) + transition_states( state, transition_length = 4, state_length = 3 ) + ease_aes('cubic-in-out') animate( redistribute_anim, start_pause = 8, end_pause = 8 )

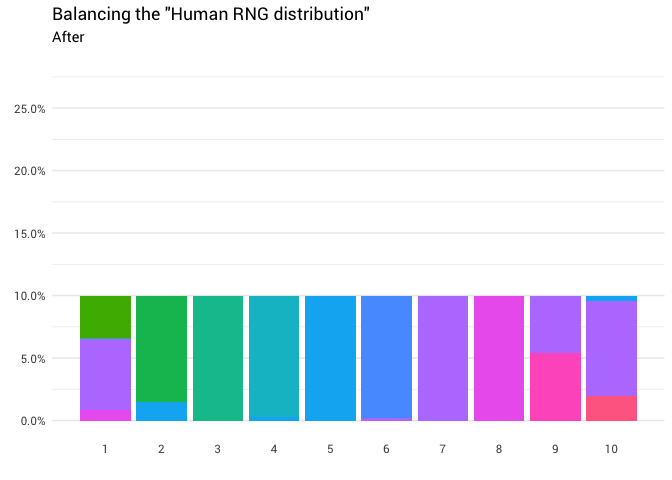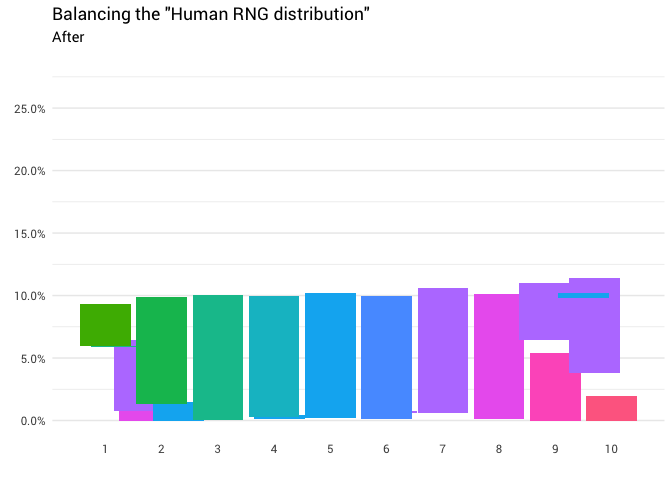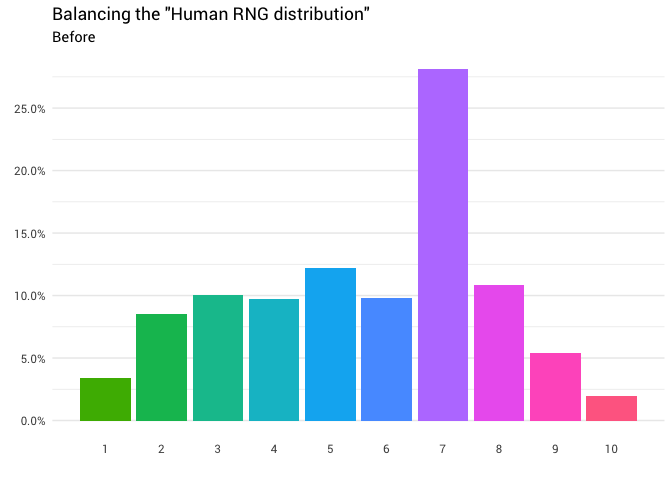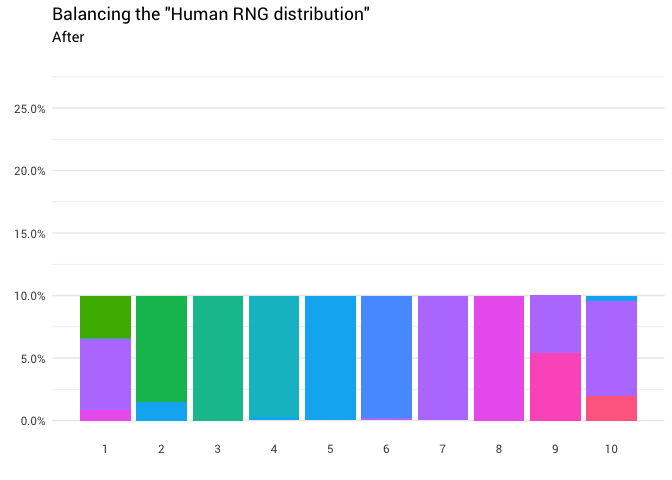
太好了！现在，我们有了重新分配功能。让我们仔细看看质量如何运动：

 balanced_probabilities %>% ggplot(aes(x = from, y = to)) + geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) + geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) + scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) + scale_fill_discrete(h = c(120, 360)) + scale_x_continuous(breaks = 1:10) + scale_y_continuous(breaks = 1:10) + theme_minimal(base_family = "Roboto") + theme(panel.grid.minor = element_blank(), panel.grid.major = element_line(linetype = "dotted"), legend.position = "none") + labs(title = "Probability mass redistribution", x = "Original number", y = "Redistributed number")

这张图说，在大约8％的情况下，当某人以随机数呼叫8时，您需要将答案作为一个单位。在其余92％的案件中，他仍然是八名。

如果我们可以使用均匀分布的随机数（从0到1）的生成器，则解决该问题将非常简单。但是我们只有一个挤满了人的房间。幸运的是，如果您准备好以一些小错误来达成协议，那么您可以从人们中获得相当不错的RNG，而无需问两次以上。

回到我们的原始分布，我们为每个数字提供以下概率，如有必要，可将其用于重新分配任何概率。

 probabilities %>% transmute(number = outcome, probability = scales::percent(p))

  ##＃小标题：10 x 2
 ##数字概率
 ## <dbl> <chr>
 ## 1 1 3.4％
 ## 2 2 8.5％
 ## 3 3 10.0％
 ## 4 4 9.7％
 ## 5 5 12.2％
 ## 6 6 9.8％
 ## 7 7 28.1％
 ## 8 8 10.9％
 ## 9 9 5.4％
 ## 10 10 1.9％

例如，当有人给我们八个随机数时，我们需要确定这八个数字是否应成为一个单位（概率为8％）。如果我们问另一个人一个随机数，那么他以8.5％的概率回答“两个”。因此，如果第二个数字为2，我们知道必须返回1作为均匀分布的随机数。

将此逻辑扩展到所有数字，我们获得以下算法：

问一个人一个随机数， $n_1$ 。
$n_1 = 1，2，3，4，6，9，$ 或 $10$ ：
您的随机数 $n_1$
如果 $n_1 = 5$ ：
向另一个人询问一个随机数（ $n_2$ ）
如果 $n_2 = 5$ （12.2％）：
您的随机数2
如果 $n_2 = 10$ （1.9％）：
您的随机数4
否则，您的随机数是5
如果 $n_1 = 7$ ：
向另一个人询问一个随机数（ $n_2$ ）
如果 $n_2 = 2$ 或 $5$ （20.7％）：
您的随机数1
如果 $n_2 = 8$ 或 $9$ （16.2％）：
您的随机数是9
如果 $n_2 = 7$ （28.1％）：
您的随机数是10
否则，您的随机数是7
如果 $n_1 = 8$ ：
向另一个人询问一个随机数（ $n_2$ ）
如果 $n_2 = 2$ （8.5％）：
您的随机数1
否则，您的随机数是8

使用此算法，您可以使一群人接近从1到10均匀分布的随机数生成器！

如何从1到10中选择一个随机数

那该怎么办呢？

如何找到这样的功能？

问题介绍

More articles: