今天,我们将看看名为Luxor的Julia语言的图形包。 这是将创建矢量图像的过程转变为伴随着情感风暴解决逻辑问题的工具之一。
注意事项 在削减后的8.5 MB轻巧的图片和gif图像中,描绘了迷幻的鸡蛋和4维物体,观看这些物体可能会引起大脑的轻微模糊!
安装方式
https ://julialang.org-从官方网站下载Julia发行版。 然后,启动解释器,将命令驱动到其控制台中:
using Pkg Pkg.add("Colors") Pkg.add("ColorSchemes") Pkg.add("Luxor")
它将安装用于颜色和Luxor本身的高级工作的软件包。
可能的问题
总体而言,尤其是开放源代码的现代编程的主要问题是,某些项目是建立在其他项目之上的,它们继承了所有错误,甚至由于不兼容而产生新的错误。 像许多其他软件包一样,卢克索在工作中也使用了其他julia软件包,这些软件包又是现有解决方案的外壳。
因此, ImageMagick.jl不想下载和保存文件。 解决方案在原始页面上找到-事实证明,他在某种程度上不喜欢西里尔字母。
Windows 7上的Cairo低级图形包出现了第二个问题。我将在这里隐藏该解决方案:
与手鼓跳舞- 我们输入解释器
]add Gtk用于gui的软件包将开始安装,并且很可能在构建过程中掉落 - 接下来,下载gtk + -bundle_3.6.4-20130513_win64
- 在安装过程中,包含Julia软件包的文件夹中的所有内容都是必需的,但是gtk尚未在项目执行过程中完成,因此我们下载了计算机的最终版本-我们将下载的存档内容放入目录C:\ Users \ User.julia \ packages \ WinRPM \ Y9QdZ \ deps \ usr \ x86_64-w64-mingw32 \ sys-root \ mingw (您的路径可能会有所不同)
- 运行julia并进入
]build Gtk然后在using Gtk ]build Gtk之后,为了更好的保真度,我们重新]build Luxor : ]build Luxor - 我们重新启动julia,我们可以放心使用所需的一切:
using Luxor
如果出现其他问题,我们将尝试找到自己的情况。
如果您想尝试动画
Luxor软件包使用ffmpeg创建动画,前提是您的计算机上存在该动画。 ffmpeg是一个跨平台的开源库,用于处理视频和音频文件,这是非常有用的( 在hub上有很好的偏移)。 安装它:
- 离线下载ffmpeg。 就我而言,这是Windows的下载
- 解压路径并将路径写入ffmpeg.exe的Path变量中。
有关路径堵塞的更多信息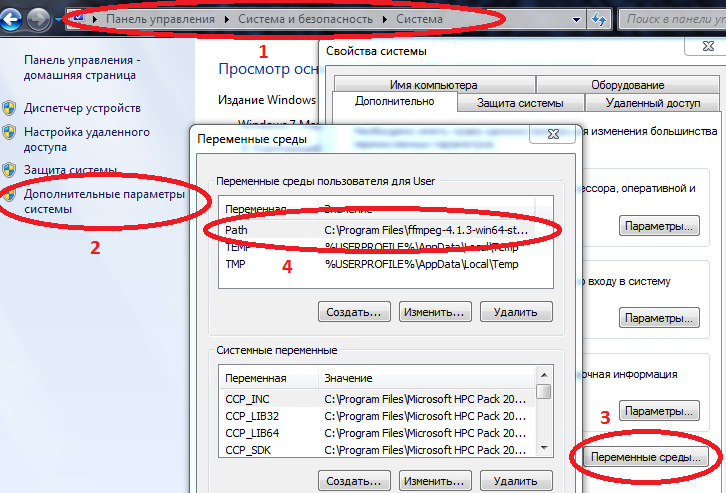
计算机/系统属性/高级系统参数/环境变量/路径 (如果没有则创建)并将路径添加到您的ffmpeg.exe中
示例C:\程序文件\ ffmpeg-4.1.3-win64-static \ bin
如果Path已经有值,则用分号将它们分开。
现在,如果将具有必要参数的ffmpeg驱动到命令控制台( cmd ),它将启动并运行,Julia仅与之通信。
世界你好
让我们从一个小陷阱开始-构建图像时,将创建一个图形文件并将其保存在工作目录中。 也就是说,在REPL中工作时,julia根文件夹将被图片阻塞,如果在Jupyter中进行绘制,则图片会堆积在项目笔记本旁边,因此,在开始工作之前,将工作目录设置在单独的位置是一个好习惯:
using Luxor cd("C:\\Users\\User\\Desktop\\mycop")
创建第一个工程图
Drawing(220, 220, "hw.png") origin() background("white") sethue("black") text("Hello world") circle(Point(0, 0), 100, :stroke) finish() preview()

Drawing()创建一个工程图,默认情况下为PNG格式,默认文件名为'luxor-drawing.png',默认尺寸为800x800,除png以外的所有格式都可以指定非整数尺寸,也可以使用纸张尺寸(“ A0 “,” A1“,” A2“,” A3“,” A4“ ...)
finish() -完成绘制并关闭文件。 您可以使用preview()在外部查看应用程序中将其打开,在Jupyter(IJulia)中工作时,它将在记事本中显示PNG或SVG文件。 在Juno中工作时,它将在“图形”面板中显示PNG或SVG文件。 在Repl中,将调用用于处理在OS中为此格式设置的图像的工具。
可以使用宏以简写形式表示
@png begin text("Hello world") circle(Point(0, 0), 100, :stroke) end
对于矢量格式EPS,SVG,PDF,一切都以相同的方式工作。
欧几里德蛋

这是一种非常有趣的画蛋方式,如果您将关键点连接起来并沿收到的线切开,就会出现出色的七巧板
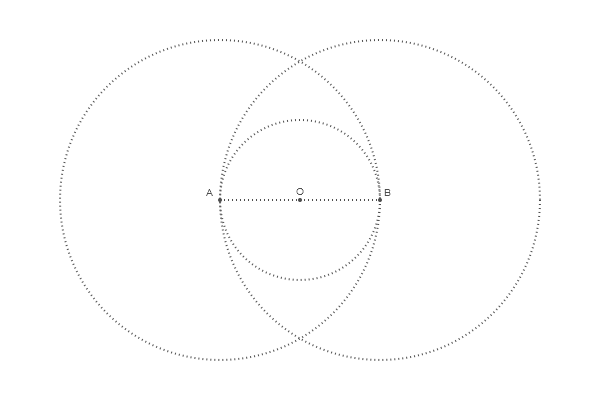
让我们从圆圈开始:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) end 200 200 "egg0"

一切都非常简单: setdash("dot") -用点绘制, sethue("gray30") -线条颜色:越小越黑,越接近100越白。 没有我们就可以定义点类,并且可以用字母O指定坐标中心(0,0) O 添加两个圆圈并在点上签名:
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke) end 600 400 "egg2"
要搜索相交点,有一个称为intersectionlinecircle()的函数可以找到直线与圆相交的一个或多个点。 因此,我们可以找到两个点,其中一个圆与通过O绘制的假想垂直线相交。由于对称性,我们只能处理圆A。
@png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
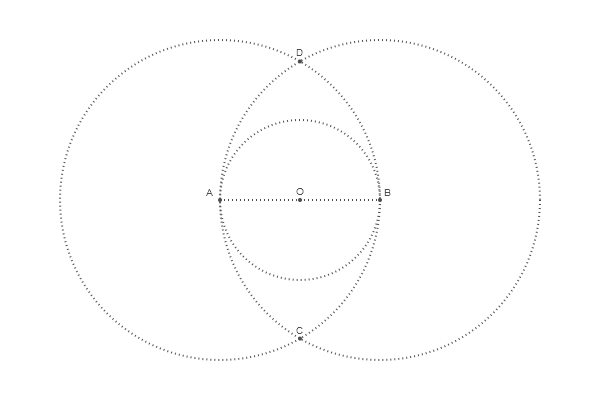
为了确定上圆的中心,我们找到相交的OD
代号 @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

辅助圆的半径由两个大圆的限制决定:
代号 @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)

鸡蛋准备好了! 它仍然需要从arc2r()函数指定的四个弧中进行组装并填写区域:
代号 @png begin radius=80 setdash("dot") sethue("gray30") A, B = [Point(x, 0) for x in [-radius, radius]] line(A, B, :stroke) circle(O, radius, :stroke) label("A", :NW, A) label("O", :N, O) label("B", :NE, B) circle.([A, O, B], 2, :fill) circle.([A, B], 2radius, :stroke)
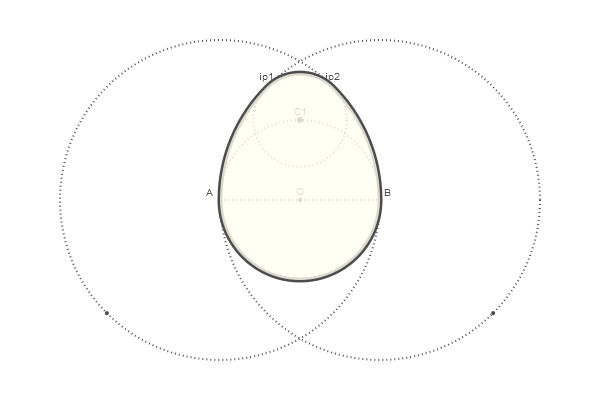
现在,为了适当地放纵自己,我们将成就
功能 function egg(radius, action=:none) A, B = [Point(x, 0) for x in [-radius, radius]] nints, C, D = intersectionlinecircle(Point(0, -2radius), Point(0, 2radius), A, 2radius) flag, C1 = intersectionlinecircle(C, D, O, radius) nints, I3, I4 = intersectionlinecircle(A, C1, A, 2radius) nints, I1, I2 = intersectionlinecircle(B, C1, B, 2radius) if distance(C1, I1) < distance(C1, I2) ip1 = I1 else ip1 = I2 end if distance(C1, I3) < distance(C1, I4) ip2 = I3 else ip2 = I4 end newpath() arc2r(B, A, ip1, :path) arc2r(C1, ip1, ip2, :path) arc2r(A, ip2, B, :path) arc2r(O, B, A, :path) closepath() do_action(action) end
我们使用随机颜色,图层绘画和各种初始条件:
@png begin setopacity(0.7) for θ in range(0, step=π/6, length=12) @layer begin rotate(θ) translate(100, 50)


除了描边和填充之外,您还可以将轮廓用作剪切区域(以蛋的形状裁剪另一个图像)或作为各种设计人员的基础。 egg()函数创建轮廓,并允许您对其执行操作。 也可以将我们的创作转换为多边形(点的数组)。 以下代码将鸡蛋的轮廓转换为多边形,然后将多边形的每个其他点移动到质心的一半。
@png begin egg(160, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) circle(pc, 5, :fill) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.5) end poly(pgon, :stroke) end 350 500 "polyegg"

默认线路连接设置会导致内部点外观不均匀。 使用setlinejoin("round")进行试验,以查看这是否会改变几何形状。 好吧,现在让我们尝试offsetpoly()在现有多边形。的内部或内部创建多边形轮廓。
@png begin egg(80, :path) pgon = first(pathtopoly()) pc = polycentroid(pgon) for pt in 1:2:length(pgon) pgon[pt] = between(pc, pgon[pt], 0.9) end for i in 30:-3:-8 randomhue() op = offsetpoly(pgon, i) poly(op, :stroke, close=true) end end 350 500 "polyeggs"

通过将路径转换为多边形而创建的点的规则性发生细微变化,并生成了不同数量的样本,它们会在连续的轮廓中不断放大。
动画制作
首先,让我们定义用于实现蛋的背景和渲染的函数,具体取决于帧号:
代号 using Colors demo = Movie(400, 400, "test") function backdrop(scene, framenumber) background("black") end function frame(scene, framenumber) setopacity(0.7) θ = framenumber * π/6 @layer begin rotate(θ) translate(100, 50) egg(50, :path) setline(10) randomhue() fillpreserve() randomhue() strokepath() end end
动画是通过一组简单的命令实现的:
animate(demo, [ Scene(demo, backdrop, 0:12), Scene(demo, frame, 0:12, easingfunction=easeinoutcubic, optarg="made with Julia") ], framerate=10, tempdirectory="C:\\Users\\User\\Desktop\\mycop", creategif=true)
究竟是什么导致我们的ffmpeg
run(`ffmpeg -f image2 -i $(tempdirectory)/%10d.png -vf palettegen -y $(seq.stitle)-palette.png`) run(`ffmpeg -framerate 30 -f image2 -i $(tempdirectory)/%10d.png -i $(seq.stitle)-palette.png -lavfi paletteuse -y /tmp/$(seq.stitle).gif`)
也就是说,创建了一系列图像,然后从这些框架中组装了一个GIF:

五角大楼
他是五核正确的四元单纯形。 为了在二维图像上绘制和处理4维对象,我们首先定义
类4维点 struct Point4D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 w::Float64 end Point4D(a::Array{Float64, 1}) = Point4D(a...) Base.size(pt::Point4D) = (4, ) Base.getindex(pt::Point4D, i) = [pt.x, pt.y, pt.z, pt.w][i] struct Point3D <: AbstractArray{Float64, 1} x::Float64 y::Float64 z::Float64 end Base.size(pt::Point3D) = (3, )
无需手动定义许多操作,我们可以将结构定义为AbstractArray的子类型( 有关作为接口的类的更多信息 )
我们必须解决的主要任务是如何将4D点转换为2D点。 让我们从一个简单的任务开始:如何将3D点转换为2D点 我们如何在平面上绘制3D图形? 考虑一个简单的立方体。 正面和背面可以具有相同的X和Y坐标,并且仅Z值有所不同。
代号 @png begin fontface("Menlo") fontsize(8) setblend(blend( boxtopcenter(BoundingBox()), boxmiddlecenter(BoundingBox()), "skyblue", "white")) box(boxtopleft(BoundingBox()), boxmiddleright(BoundingBox()), :fill) setblend(blend( boxmiddlecenter(BoundingBox()), boxbottomcenter(BoundingBox()), "grey95", "grey45" )) box(boxmiddleleft(BoundingBox()), boxbottomright(BoundingBox()), :fill) sethue("black") setline(2) bx1 = box(O, 250, 250, vertices=true) poly(bx1, :stroke, close=true) label.(["-1 1 1", "-1 -1 1", "1 -1 1", "1 1 1"], slope.(O, bx1), bx1) setline(1) bx2 = box(O, 150, 150, vertices=true) poly(bx2, :stroke, close=true) label.(["-1 1 0", "-1 -1 0", "1 -1 0", "1 1 0"], slope.(O, bx2), bx2, offset=-45) map((x, y) -> line(x, y, :stroke), bx1, bx2) end 400 400 "cube.png"

因此,想法是将一个多维数据集从3D投影到2D,保存前两个值,然后将它们乘以或更改为第三个值。 检查一下
如何运作 const K = 4.0 function convert(Point, pt3::Point3D) k = 1/(K - pt3.z) return Point(pt3.x * k, pt3.y * k) end @png begin cube = Point3D[ Point3D(-1, -1, 1), Point3D(-1, 1, 1), Point3D( 1, -1, 1), Point3D( 1, 1, 1), Point3D(-1, -1, -1), Point3D(-1, 1, -1), Point3D( 1, -1, -1), Point3D( 1, 1, -1), ] circle.(convert.(Point, cube) * 300, 5, :fill) end 220 220 "points"

使用相同的原理,我们创建一种转换4D点的方法,并创建一个函数,该函数将获取一个二维点列表并将它们两次映射到一个适合绘制的二维点列表中。
function convert(Point3D, pt4::Point4D) k = 1/(K - pt4.w) return Point3D(pt4.x * k, pt4.y * k, pt4.z * k) end function flatten(shape4) return map(pt3 -> convert(Point, pt3), map(pt4 -> convert(Point3D, pt4), shape4)) end
接下来,设置顶点和面并检查其颜色如何
! const n = -1/√5 const pentachoron = [Point4D(vertex...) for vertex in [ [ 1.0, 1.0, 1.0, n], [ 1.0, -1.0, -1.0, n], [-1.0, 1.0, -1.0, n], [-1.0, -1.0, 1.0, n], [ 0.0, 0.0, 0.0, n + √5]]]; const pentachoronfaces = [ [1, 2, 3], [1, 2, 4], [1, 2, 5], [1, 3, 4], [1, 3, 5], [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]; @png begin setopacity(0.2) pentachoron2D = flatten(pentachoron) for (n, face) in enumerate(pentachoronfaces) randomhue() poly(1500 * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end 300 250 "5ceil"

每个自重的游戏开发人员都应该了解机器图形学的数学基础 。 如果您从未尝试过在OpenGL中压缩,旋转或反射茶壶 -不用担心,一切都非常简单。 要相对于直线反射点或使平面绕特定轴旋转,您需要将坐标乘以特殊矩阵。 实际上,我们将确定所需的转换矩阵:
接更多 function XY(θ) [cos(θ) -sin(θ) 0 0; sin(θ) cos(θ) 0 0; 0 0 1 0; 0 0 0 1] end function XW(θ) [cos(θ) 0 0 -sin(θ); 0 1 0 0; 0 0 1 0; sin(θ) 0 0 cos(θ)] end function XZ(θ) [cos(θ) 0 -sin(θ) 0; 0 1 0 0; sin(θ) 0 cos(θ) 0; 0 0 0 1] end function YZ(θ) [1 0 0 0; 0 cos(θ) -sin(θ) 0; 0 sin(θ) cos(θ) 0; 0 0 0 1] end function YW(θ) [1 0 0 0; 0 cos(θ) 0 -sin(θ); 0 0 1 0; 0 sin(θ) 0 cos(θ)] end function ZW(θ) [1 0 0 0; 0 1 0 0; 0 0 cos(θ) -sin(θ); 0 0 sin(θ) cos(θ)]; end function rotate4(A, matrixfunction) return map(A) do pt4 Point4D(matrixfunction * pt4) end end
通常,您相对于一维对象在平面上旋转点。 3D点围绕2D线(通常是XYZ轴之一)。 因此,合乎逻辑的是4D点相对于3D平面旋转。 我们已经确定了绕由两个轴X,Y,Z和W定义的平面执行四维旋转的矩阵。XY平面通常是绘图表面的平面。 如果您将XY平面视为计算机屏幕,则XZ平面平行于您的桌子或地板,而YZ平面是您桌子右侧或左侧旁边的墙壁。 但是XW,YW和ZW呢? 这是四维图形的奥秘:我们看不到这些平面,我们只能通过观察形式如何通过它们并围绕它们移动来想象它们的存在。
现在,我们为框架设置功能并缝制动画:
扰流板 using ColorSchemes function frame(scene, framenumber, scalefactor=1000) background("white")

好吧,另一个角度:
代号 function frame(scene, framenumber, scalefactor=1000) background("antiquewhite") setlinejoin("bevel") setline(1.0) setopacity(0.2) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) pentachoron2D = flatten( rotate4( pentachoron, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(pentachoronfaces) sethue(get(ColorSchemes.diverging_rainbow_bgymr_45_85_c67_n256, n/length(pentachoronfaces))) poly(scalefactor * pentachoron2D[face], :fillpreserve, close=true) sethue("black") strokepath() end end makemovie(500, 500, "pentachoron-xz-yw.gif", scalefactor=2000)
实现更流行的三维物体Tesseract的愿望是完全自然的。
上衣和面孔 const tesseract = [Point4D(vertex...) for vertex in [ [-1, -1, -1, 1], [ 1, -1, -1, 1], [ 1, 1, -1, 1], [-1, 1, -1, 1], [-1, -1, 1, 1], [ 1, -1, 1, 1], [ 1, 1, 1, 1], [-1, 1, 1, 1], [-1, -1, -1, -1], [ 1, -1, -1, -1], [ 1, 1, -1, -1], [-1, 1, -1, -1], [-1, -1, 1, -1], [ 1, -1, 1, -1], [ 1, 1, 1, -1], [-1, 1, 1, -1]]] const tesseractfaces = [ [1, 2, 3, 4], [1, 2, 10, 9], [1, 4, 8, 5], [1, 5, 6, 2], [1, 9, 12, 4], [2, 3, 11, 10], [2, 3, 7, 6], [3, 4, 8, 7], [5, 6, 14, 13], [5, 6, 7, 8], [5, 8, 16, 13], [6, 7, 15, 14], [7, 8, 16, 15], [9, 10, 11, 12], [9, 10, 14, 13], [9, 13, 16, 12], [10, 11, 15, 14], [13, 14, 15, 16]];
创建动画 function frame(scene, framenumber, scalefactor=1000) background("black") setlinejoin("bevel") setline(10.0) setopacity(0.7) eased_n = scene.easingfunction(framenumber, 0, 1, scene.framerange.stop) tesseract2D = flatten( rotate4( tesseract, XZ(eased_n * 2π) * YW(eased_n * 2π))) for (n, face) in enumerate(tesseractfaces) sethue([Luxor.lighter_blue, Luxor.lighter_green, Luxor.lighter_purple, Luxor.lighter_red][mod1(n, 4)]...) poly(scalefactor * tesseract2D[face], :fillpreserve, close=true) sethue([Luxor.darker_blue, Luxor.darker_green, Luxor.darker_purple, Luxor.darker_red][mod1(n, 4)]...) strokepath() end end makemovie(500, 500, "tesseract-xz-yw.gif", scalefactor=1000)

作业:自动创建坐标和顶点编号的数组( 分别带有重复和不带有重复的排列 )。 同样,我们没有使用所有的翻译矩阵。 每个新的视角都会带来一个新的“哇!”,但我决定不使页面超载。 好吧,您可以尝试许多面孔和尺寸。
参考文献