🥐 💪🏼 🧒🏿 在轴承振动诊断过程中消除振动传感器信号中的高频噪声 🧒🏾 🧚🏽 🚢

引言

数字信号处理最紧迫的任务之一是清除信号中的噪声的任务。任何实际的信号不仅包含有用的信息，而且还包含一些干扰或噪声的外来影响的痕迹。另外，在振动诊断期间，来自振动传感器的信号具有不稳定的频谱，这使滤波任务变得复杂。

有许多种方法可以消除信号中的高频噪声。例如，Scipy库包含基于各种过滤方法的过滤器。通过沿时间轴等对信号进行平均来平滑信号。

但是，离散小波变换（DWT）方法的优点是各种小波形状。您可以选择一个小波，该小波将具有预期现象的形式特征。例如，您可以选择给定频率范围内的信号，该信号的形状会导致出现缺陷。

该出版物的目的是分析使用DWT信号转换，卡尔曼滤波器和移动平均法对振动传感器的信号进行滤波的方法。

用于分析的源数据

在该出版物中，将使用NASA数据集分析基于各种过滤方法的过滤器的操作。在实验平台PRONOSTIA上获得的数据：

该套件包含有关各种轴承磨损的振动传感器信号的数据。下表列出了带有信号文件的文件夹的用途：

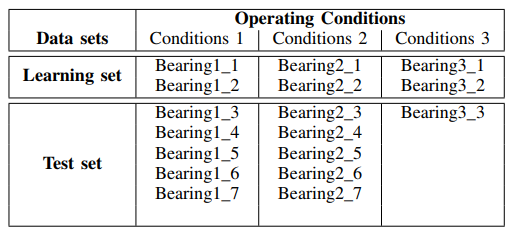
通过振动传感器（水平和垂直加速度计），力和温度的信号来监控轴承的状态。

收到三种不同负载的信号：

第一工作条件：1800 rpm和4000 N；
第二工作条件：1650 rpm和4200 N；
第三工作条件：1500 rpm和5000N。

对于这些情况，使用连续小波信号转换，我们为测试集中的数据构造光谱功率刻度图 -从文件夹中找到一个文件（对于一种类型的轴承）：['Test_set / Bearing1_3 / acc_00001.csv'，'Test_set / Bearing2_3 / acc_00001。 csv'，'Test_set / Bearing3_3 / acc_00001.csv']（请参见表1）。

比例图列表

import scaleogram as scg import pandas as pd from pylab import * import pywt filename_n = ['Test_set/Bearing1_3/acc_00001.csv', 'Test_set/Bearing2_3/acc_00001.csv', 'Test_set/Bearing3_3/acc_00001.csv'] for filename in filename_n: df = pd.read_csv(filename, header=None) signal = df[4].values wavelet = 'cmor1-0.5' ax = scg.cws(signal, scales=arange(1, 40), wavelet=wavelet, figsize=(8, 4), cmap="jet", cbar=None, ylabel=' ', xlabel=" ", yscale="log", title='-  %s \n( )'%filename) show()

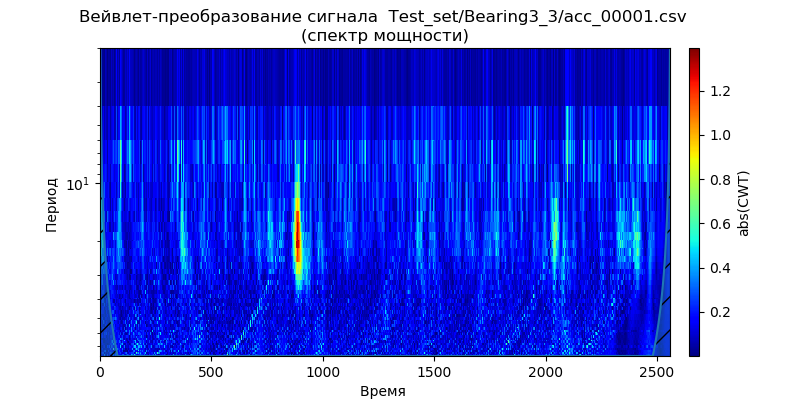
从给定的比例图可以看出，频谱功率增加的时刻在时间上较早发生，并表现出以下操作条件的周期性：1650 rpm和4200 N，这表明轴承在此频段的加速降解是为了减小力。我们将使用该信号（“ Test_set / Bearing2_3 / acc_00001.csv”）来分析噪声消除方法。

使用DWT进行信号解构

在出版物中，我们看到了如何在DWT上实现滤波器组，该滤波器组可以将信号解构为其频率子带。近似系数（cA）表示信号（平均滤波器）的低频部分。细节系数（cD）表示信号的高频部分。接下来，我们将研究如何使用DWT将信号解构为其频率子带并恢复原始信号。

有两种方法可以使用PyWavelets工具解决信号解构问题：

第一种方法是将pywt.dwt（）应用于信号以提取近似系数和细节系数（cA1，cD1）。然后，为了恢复信号，我们将使用pywt.idwt（）：

上市

 import pywt from scipy import * import pandas as pd from pylab import * filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values (cA1, cD1) = pywt .dwt (signal, 'db2', 'smooth') r_signal = pywt.idwt (cA1, cD1, 'db2', 'smooth') fig, ax =subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r', label='  ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title('   ( pywt.dwt()) \n   ( pywt.idwt()) ') show()

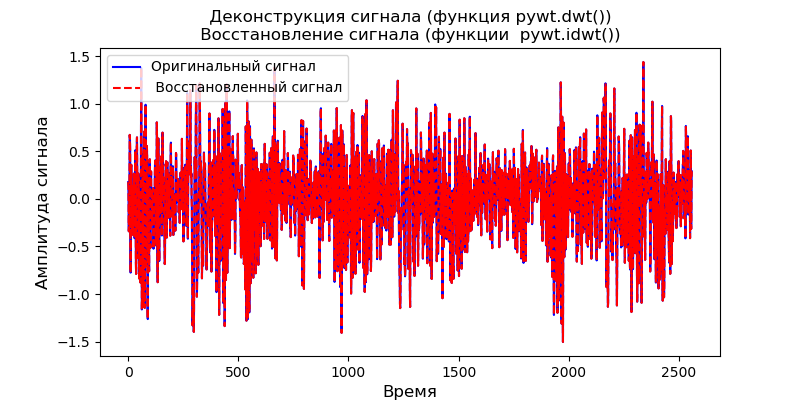
将pywt.wavedec（）函数应用于信号的第二种方法是将所有近似系数和细节系数恢复到一定水平。此函数将输入信号和电平作为输入，并返回一组近似系数（第n级）和n组详细系数（从1至第n级）。对于解构，应用pywt.waverec（）：

上市

 import pywt import pandas as pd from pylab import * filename = 'Test_set/Bearing3_3/acc_00026.csv' df = pd.read_csv(filename, header=None) signal = df[4].values coeffs = pywt.wavedec(signal, 'db2', level=8) r_signal = pywt.waverec(coeffs, 'db2') fig, ax = plt.subplots(figsize=(8,4)) ax.plot(signal, 'b',label=' ') ax.plot(r_signal, 'r ',label= ' ', linestyle='--') ax.legend(loc='upper left') ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) ax.set_title('    - level.\n   ( pywt.wavedec()) ') show()

解构和恢复信号的第二种方法更加方便，它使您可以立即设置所需的解构级别。

通过消除信号解构过程中的一些细节系数来消除高频噪声

我们将通过删除一些细节系数来恢复信号。由于细节系数代表信号的高频部分，因此我们只过滤频谱的这一部分。如果信号中存在高频噪声，则这是对其进行滤波的一种方法。

在PyWavelets库中，可以使用阈值处理函数pywt.threshol（）完成此操作：

pywt.threshold（data，value，mode ='soft'，替代= 0）¶
数据： array_like
数值数据。
值：标量
阈值。
模式： {“软”，“硬”，“粗纱”，“更大”，“更少”}
定义将应用于输入的阈值类型。 默认为“软”。
替代：浮动，可选
替代值（默认值：0）。
输出：数组
阈值数组。

最好使用以下示例考虑对给定阈值应用阈值处理功能：

 >>>> from scipy import* >>> import pywt >>> data =linspace(1, 4, 7) >>> data array([1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'soft') array([0. , 0. , 0. , 0.5, 1. , 1.5, 2. ]) >>> pywt.threshold(data, 2, 'hard') array([0. , 0. , 2. , 2.5, 3. , 3.5, 4. ]) >>> pywt.threshold(data, 2, 'garrote') array([0. , 0. , 0., 0.9,1.66666667, 2.35714286, 3.])

我们使用以下清单绘制阈值函数图：

上市

 from scipy import* from pylab import* import pywt s = linspace(-4, 4, 1000) s_soft = pywt.threshold(s, value=0.5, mode='soft') s_hard = pywt.threshold(s, value=0.5, mode='hard') s_garrote = pywt.threshold(s, value=0.5, mode='garrote') figsize=(10, 4) plot(s, s_soft) plot(s, s_hard) plot(s, s_garrote) legend(['soft (0.5)', 'hard (0.5)', 'non-neg. garrote (0.5)']) xlabel('   ') ylabel('  ') show()

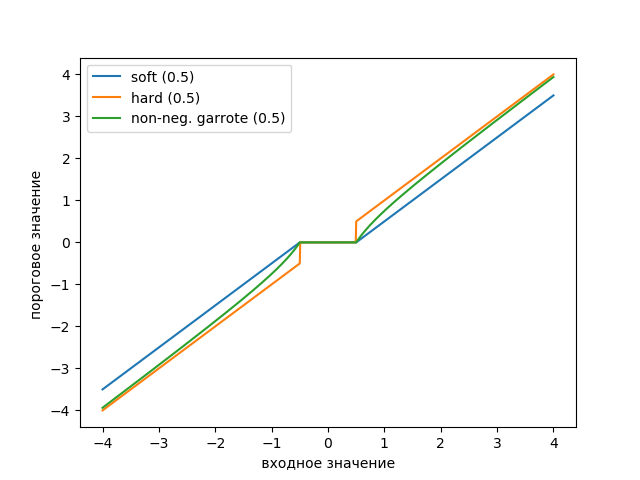
该图显示非负Garott阈值介于软阈值和硬阈值之间。需要一对用于定义过渡区域宽度的阈值。

阈值函数对滤波器特性的影响

从上图可以看出，只有两个阈值函数“ soft”和“ garrote”适合我们，为了研究它们对滤波器特性的影响，我们写下清单：

上市

 import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=['soft' ,'garrote'] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode=w ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT  ', linewidth=2) ax.legend() ax.set_title('      :%s\n   :%s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

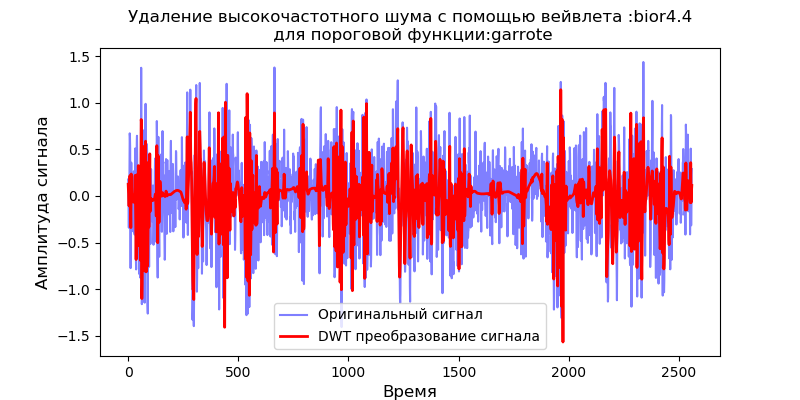
从图中可以看出，软功能比“ garrote”功能提供了更好的平滑度，因此将来我们将使用软功能。

细节阈值对滤波器特性的影响

对于所考虑的滤波器类型，更改详细系数的阈值是一个重要特性，因此，我们使用以下列表研究其效果：

上市

 import pandas as pd from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values v='bior4.4' thres=[0.1,0.4,0.6] for w in thres: def lowpassfilter(signal, thresh, wavelet=v): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, level=8,mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label=' ') rec = lowpassfilter(signal,w) ax.plot(rec, 'r', label='DWT  ', linewidth=2) ax.legend() ax.set_title('      :%s\n    %s'%(v,w), fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

从获得的图形中可以看出，细节级别阈值会影响筛选零件的比例。随着阈值的增加，小波会减去不断增加的噪声，直到细节比例过度增大，并且变换开始使原始信号的形状失真为止，对于我们的信号，阈值应不高于0.63。

小波对滤波器特性的影响

PyWavelets库具有足够的DWT转换小波，可以通过以下方式获得：

 >>> import pywt >>> print(pywt.wavelist(kind= 'discrete')) ['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'haar', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']

小波对滤波器特性的影响取决于其原始函数。为了证明这种依赖性，我们从Dobeshi族中选择了两个小波-db1和db38，并考虑以下族：

上市

 import pywt from pylab import* db_wavelets = ['db1', 'db38'] fig, axarr = subplots(ncols=2, nrows=5, figsize=(14,8)) fig.suptitle('  : db1,db38', fontsize=14) for col_no, waveletname in enumerate(db_wavelets): wavelet = pywt.Wavelet(waveletname) no_moments = wavelet.vanishing_moments_psi family_name = wavelet.family_name for row_no, level in enumerate(range(1,6)): wavelet_function, scaling_function, x_values = wavelet.wavefun(level = level) axarr[row_no, col_no].set_title("{} : {}.   : {}. :: {} ".format( waveletname, level, no_moments, len(x_values)), loc='left') axarr[row_no, col_no].plot(x_values, wavelet_function, 'b--') axarr[row_no, col_no].set_yticks([]) axarr[row_no, col_no].set_yticklabels([]) tight_layout() subplots_adjust(top=0.9) show()

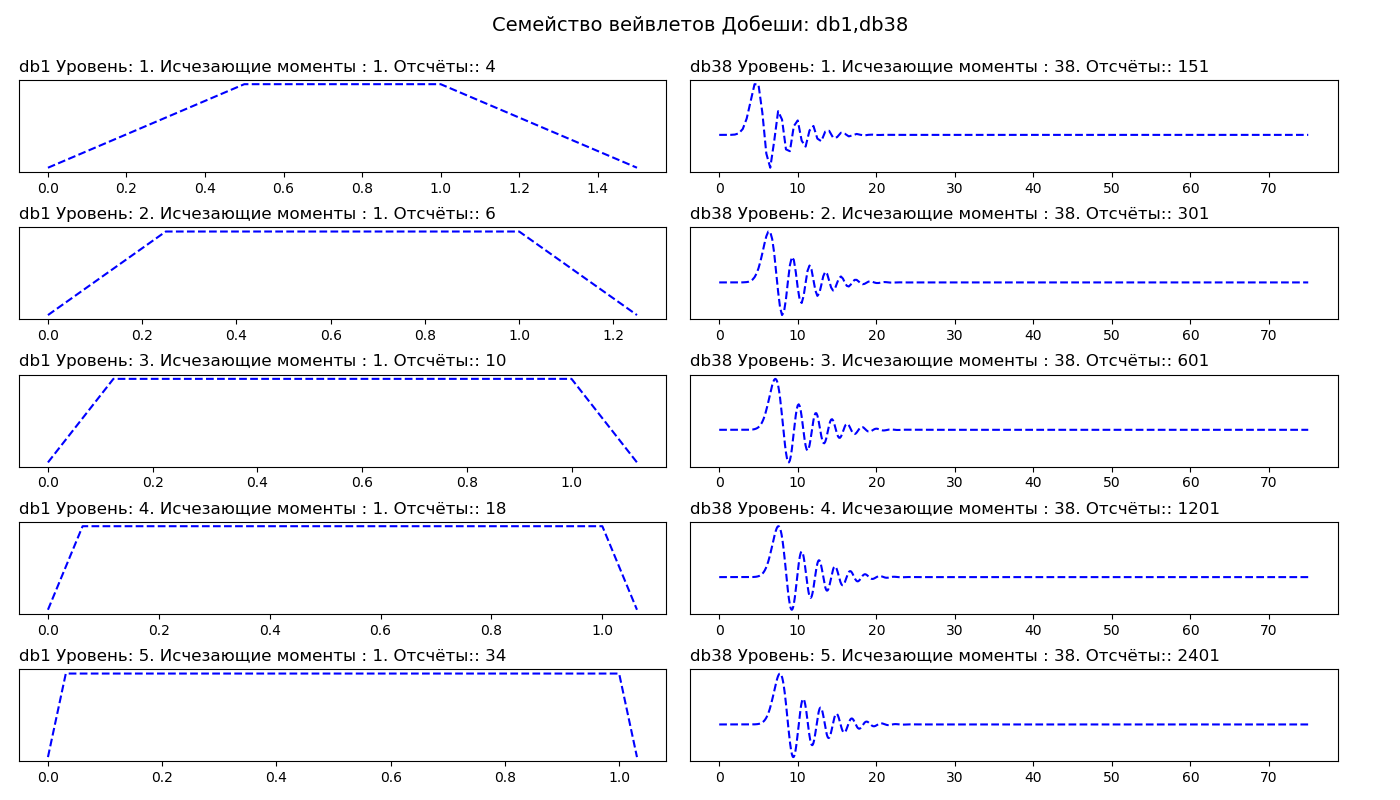
在第一列中，我们看到一阶（db1）的Daubeshi小波，在38阶（db38）的第二列中。因此，db1有一个灭绝时刻，而db38有38个灭绝时刻。消失的时刻数与小波的近似顺序和平滑度有关。如果小波具有P个消失点，则它可以近似为P-1的多项式。

更平滑的子波可以创建更平滑的信号逼近，反之亦然-“短”子波可以更好地跟踪近似函数的峰值。选择小波时，我们还可以指示分解级别。默认情况下，PyWavelets选择输入信号可能的最大分解级别。最大分解级别取决于输入信号和小波的长度：

上市

 import pandas as pd import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) data = df[4].values w=['db1', 'db38'] for v in w: n_level=pywt.dwt_max_level(len(data),v) print('  %s   : %s ' %(v,n_level))

对于db1小波，最大分解级别：11
对于db38小波，最大分解级别：5

对于小波分解的最大级别的获得值，我们考虑使用滤波器来去除高频噪声：

上市

 import pandas as pd import scaleogram as scg from pylab import * import pywt filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values discrete_wavelets =[('db38', 5),('db1',11)] for v in discrete_wavelets: def lowpassfilter(signal, thresh = 0.63, wavelet=v[0]): thresh = thresh*nanmax(signal) coeff = pywt.wavedec(signal, wavelet, mode="per" ) coeff[1:] = (pywt.threshold(i, value=thresh, mode='soft' ) for i in coeff[1:]) reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" ) return reconstructed_signal wavelet = pywt.DiscreteContinuousWavelet(v[0]) phi, psi, x = wavelet.wavefun(level=v[1]) fig, ax = subplots(figsize=(8,4)) ax.set_title("   : %s,level=%s"%(v[0],v[1]), fontsize=12) ax.plot(x,phi,linewidth=2) fig, ax = subplots(figsize=(8,4)) ax.plot(signal, color="b", alpha=0.5, label='   ') rec = lowpassfilter(signal, 0.4) ax.plot(rec, 'r', label='DWT  ', linewidth=2) ax.legend() ax.set_title('   \n   :%s,level=%s'%(v[0],v[1]),fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) wavelet = 'cmor1-0.5' ax = ax = scg.cws(rec, scales=arange(1,128), wavelet=wavelet,figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT  \n(   DWT  )') show()

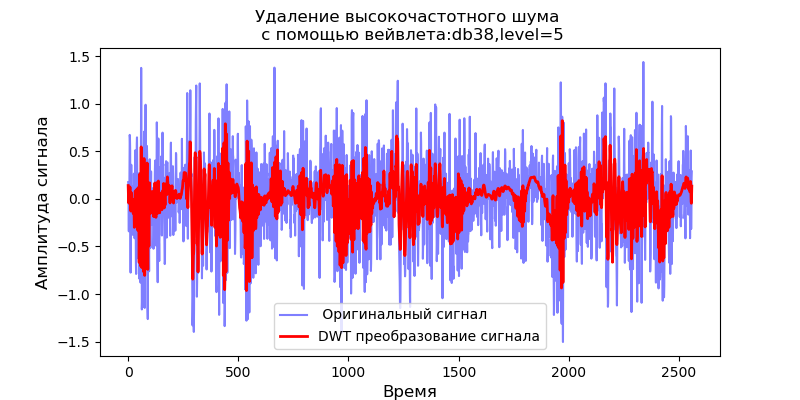
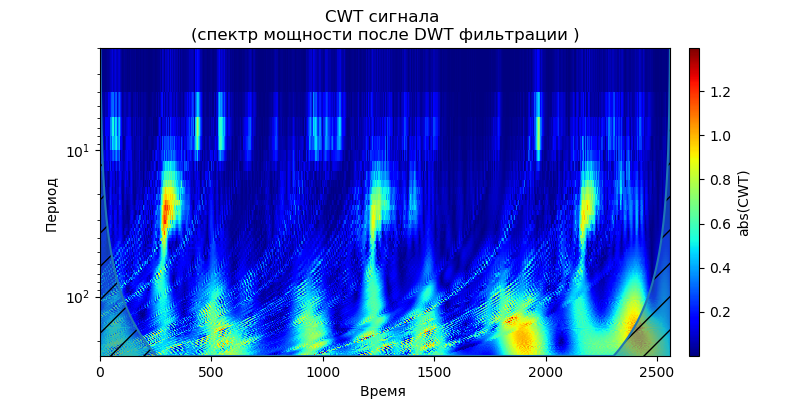
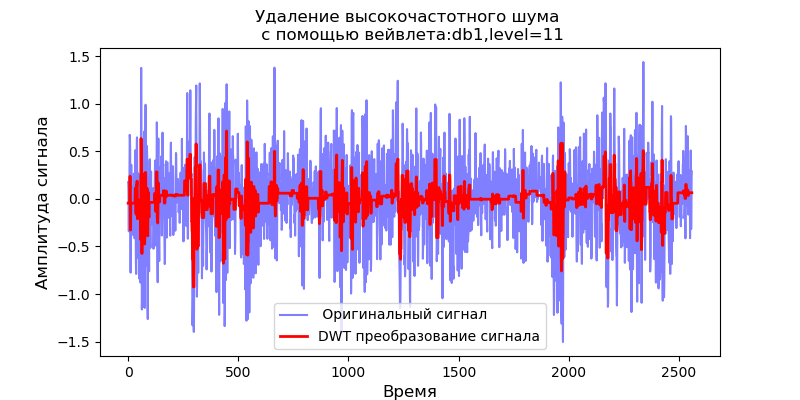
从滤波器输出端给定的信号比例图可以得出，对于db38小波，频谱的峰值功率后面是局部区域，对于db1小波，这些区域消失了。应当注意，例如，db38小波可以近似37度多项式的信号。这扩展了信号的分类，例如，根据振动传感器的信号来识别设备故障。

由于具有Daubechies小波的滤波器之后的信号使用近似和分解系数作为序列的特征形成一个时间序列，因此可以确定此类序列的接近程度，从而极大地简化了它们的搜索和分类

卡尔曼滤波器消除高频噪声

卡尔曼滤波器广泛用于过滤各种动态系统中的噪声。考虑具有状态向量x的动力学系统。

（ ）

$x = F \ cdot x + w（Q）$

其中F是转移矩阵
w（Q）是一个具有零数学期望和一个协方差矩阵Q的随机过程（噪声）。

我们将在每个时间点以已知的测量误差观察系统的状态转换。使用卡尔曼方法消除噪声包括两个步骤-外推和校正，看起来像这样。

设置系统参数：

噪声协方差（过程噪声协方差）的Q矩阵。
H是观察矩阵（测量值）。
R-观察噪声的协方差（测量噪声的协方差）。
P = Q是状态向量的协方差矩阵的初始值。
z（t）是系统的观察状态。
x = z（0）是系统状态的初始值。

对于每个观察值z，我们将计算滤波后的状态x
为此，我们执行以下步骤。

•步骤1：外推
1.系统状态的外推（预测）

$x = F \ cdot x$
2.计算外推状态向量的协方差矩阵

$F = F \ cdot P \ cdot F ^ {T} + Q$

•步骤2：更正
1.计算误差向量，即观测值与预期状态的偏差

$y = z-H \ cdot x$
2.计算偏差向量（误差向量）的协方差矩阵

$S = H \ cdot P \ cdot H ^ {T} + R$
3.计算卡尔曼增益

$K = P \ cdot H \ cdot H ^ {T} \ cdot S ^ {-1}$
4.修正状态向量估计

$x = x + K \ cdot y$
5.我们校正协方差矩阵以估计系统状态向量

（ ）

$P =（I-K \ cdot H）\ cdot P$

清单用于算法的实现

 from scipy import* from pylab import* import pandas as pd def kalman_filter( z, F = eye(2), #     (transitionMatrix) Q = eye(2)*3e-3, #   (processNoiseCov) H = eye(2), #   (measurement) R = eye(2)*3e-1 #    (measurementNoiseCov) ): n = z.shape[0] #   #m = z.shape[1] #   x = z[0,:].transpose() #      P = Q #       r = [ x ] #  for i in range(1,n): # : x = F.dot( x ) #  ()   P = F.dot(P).dot( F.transpose() ) + Q #       # : y = z[i] - H.dot(x) #  ,      ()  S = H.dot(P).dot(H.transpose()) + R #      ( ) K = P.dot(H.transpose()).dot(linalg.inv(S)) #     x = x + K.dot(y) #     P = ( eye(z.shape[1]) - K.dot(H) ).dot(P) #       r.append( x.transpose()) return array(r) filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values N= signal .shape[0] #   # 2 dimensions y0 =linspace(0.0,2500.0,N) y1 =signal d = array(list(zip(y0,y1))) dn = dr = kalman_filter(dn) fig, ax = subplots(figsize=(8,4)) ax.plot( d[:,0], d[:,1],'b', label=' ' ) ax.plot( r[:,0], r[:,1],'r', label='kalman' ) ax.legend(loc='upper left') ax.set_title('       \n (  )', fontsize=12) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) show()

对于给定的动态模型，可以使用pyKalman库：

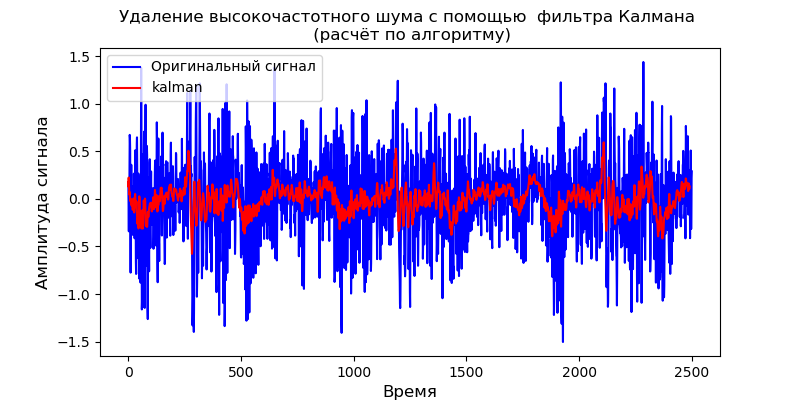
上市

 from pykalman import KalmanFilter import pandas as pd from pylab import * import scaleogram as scg filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) signal = df[4].values measurements =signal kf = KalmanFilter(transition_matrices=[1] ,# A      t  t+1 observation_matrices=[1],# C   initial_state_mean=measurements[0],#   initial_state_covariance=[1],#    observation_covariance=[1],# R    transition_covariance= 0.01) # Q     state_means, state_covariances = kf.filter(measurements)# ,   state_means=[w[0] for w in state_means] state_std = sqrt(state_covariances[:,0]) fig, ax = subplots(figsize=(8,4)) ax.plot(measurements ,'b', label=' ') ax.plot(state_means ,'r', label='kalman- ') ax.legend() ax.set_title('      \n ( pyKalman)', fontsize=14) ax.set_ylabel(' ', fontsize=12) ax.set_xlabel('', fontsize=12) wavelet = 'cmor1-0.5' ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT    \n( )') ax = ax = scg.cws(state_means, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT     \n(  )') show()

卡尔曼滤波器可以很好地消除高频噪声，但是，它不允许更改输出信号的形状。

移动平均法

在确定强振荡序列变化的主要方向时，出现了使用移动平均法将其平滑掉的问题。这可能是汽车中油位传感器的读数，或者像我们一样，是有关轴承加速退化的高频传感器的数据。该问题可以被认为是某些序列r的叠加噪声的恢复。

简称简单移动平均线-SMA（简单移动平均线）。计算当前过滤器值

$r_ {i}$ 我们只是对序列的前n个元素求平均值，因此过滤器将开始处理序列n的元素。

（ ）

$r_ {i} = \ frac {1} {n} \ cdot \ sum_ {j = 1} ^ {n} y _ {（i-j）}; i> n$

上市

 <source lang="python">from scipy import * import pandas as pd from pylab import * import pywt import scaleogram as scg def get_ave_values(xvalues, yvalues, n = 6): signal_length = len(xvalues) if signal_length % n == 0: padding_length = 0 else: padding_length = n - signal_length//n % n xarr = array(xvalues) yarr = array(yvalues) xarr.resize(signal_length//n, n) yarr.resize(signal_length//n, n) xarr_reshaped = xarr.reshape((-1,n)) yarr_reshaped = yarr.reshape((-1,n)) x_ave = xarr_reshaped[:,0] y_ave = nanmean(yarr_reshaped, axis=1) return x_ave, y_ave def plot_signal_plus_average(time, signal, average_over = 5): fig, ax = subplots(figsize=(8, 4)) time_ave, signal_ave = get_ave_values(time, signal, average_over) ax.plot(time_ave, signal_ave,"b", label = '   (n={})'.format(5)) ax.set_xlim([time[0], time[-1]]) ax.set_ylabel(' ', fontsize=12) ax.set_title('     SMA', fontsize=14) ax.set_xlabel('', fontsize=12) ax.legend() return signal_ave filename = 'Test_set/Bearing2_3/acc_00001.csv' df = pd.read_csv(filename, header=None) df_nino = df[4].values N = df_nino.shape[0] time = arange(0, N) signal = df_nino signal_ave=plot_signal_plus_average(time, signal) wavelet = 'cmor1-0.5' ax = ax = scg.cws(signal, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4),cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT  %s \n(     )'%filename) ax = ax = scg.cws(signal_ave, scales=arange(1,40), wavelet=wavelet, figsize=(8, 4), cmap="jet", ylabel=' ', xlabel=" ", yscale="log", title='CWT  %s \n(    )'%filename) show()

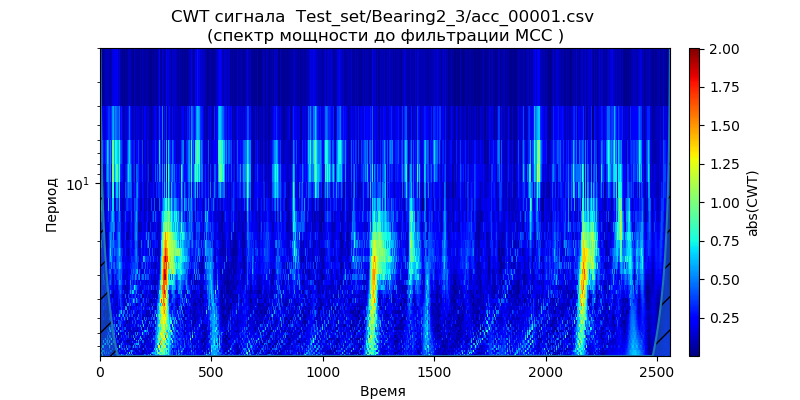
从比例图可以看出，SMA方法不能很好地清除高频噪声中的信号，并且
如上所述用于平滑。

结论：

使用比例尺模块，针对相同类型的轴承，在不同的测试条件下获得了三个测试振动传感器信号的CWT小波比例尺。根据比例图数据，选择了清晰显示后期退化迹象的信号。在给出的所有示例中，此信号均用于演示滤波器的操作。
对于给定的小波水平，考虑了使用PyWavelets库的DWT解构和恢复振动传感器信号的方法，这些模块使用pywt.dwt（），pywt.idwt（）和pywt.wavedec（）模块。
这些示例说明了pywt.threshol（）模块用于过滤DWT详细系数的应用功能，这些细节系数使用给定阈值的阈值函数负责频谱的高频部分。
考虑了反导DWT小波对消除噪声的信号形状的影响。
获得了动态介质的卡尔曼滤波器模型，并根据振动传感器的测试信号对该模型进行了测试。噪声消除图与使用pyKalman模块获得的图相同。图的性质与比例图一致。
.

在轴承振动诊断过程中消除振动传感器信号中的高频噪声

引言