
本文的翻译是专门为“开发人员算法”课程的学生准备的。
金字塔排序(或堆排序,HeapSort)是一种基于数据结构(例如二进制堆)的比较排序方法。 这类似于按选择排序,在这种情况下,我们首先查找最大元素,然后将其放在最后。 接下来,我们对其余元素重复相同的操作。
首先定义一个完整的二叉树。 完成的二叉树是一种二叉树,其中每个级别(除了最后一个级别)都有完整的节点集,所有叶子都位于左侧(来源Wikipedia )。
二进制堆是完整的二进制树,其中的元素以特殊顺序存储:父节点中的值大于(或小于)其两个子节点中的值。 第一个选项称为max-heap,第二个称为min-heap。 堆可以由二叉树或数组表示。
为什么将基于数组的表示形式用于二进制堆?
由于二进制堆是完整的二进制树,因此可以很容易地将其表示为数组,并且基于数组的表示在内存消耗方面非常有效。 如果父节点存储在索引I中,则可以将左子节点计算为2 I + 1,而将右子节点计算为2 I + 2(前提是索引从0开始)。
金字塔形升序排序算法:
- 从输入构建最大堆。
- 在这一阶段,最大的元素存储在堆的根目录中。 将其替换为堆的最后一个元素,然后将其大小减小1。最后,使用新的根将结果树转换为max-heap。
- 重复上述步骤,直到堆大小大于1。
如何堆一堆?
仅当节点的子节点已经转换时,才可以将堆转换过程(以下称为堆化过程)应用于该节点。 因此,必须从下至上执行转换。 让我们用一个例子弄清楚:
: 4, 10, 3, 5, 1 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) . heapify 1: 4(0) / \ 10(1) 3(2) / \ 5(3) 1(4) heapify 0: 10(0) / \ 5(1) 3(2) / \ 4(3) 1(4) heapify .
建议:在继续解决方案之前,请先解决“实践”上的问题 。
C ++
// C++ #include <iostream> using namespace std; // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { swap(arr[i], arr[largest]); // heapify(arr, n, largest); } } // , void heapSort(int arr[], int n) { // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // swap(arr[0], arr[i]); // heapify heapify(arr, i, 0); } } /* n*/ void printArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // int main() { int arr[] = {12, 11, 13, 5, 6, 7}; int n = sizeof(arr)/sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
爪哇
// Java public class HeapSort { public void sort(int arr[]) { int n = arr.length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int arr[], int n, int i) { int largest = i; // int l = 2*i + 1; // = 2*i + 1 int r = 2*i + 2; // = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // public static void main(String args[]) { int arr[] = {12, 11, 13, 5, 6, 7}; int n = arr.length; HeapSort ob = new HeapSort(); ob.sort(arr); System.out.println("Sorted array is"); printArray(arr); } }
巨蟒
# Python # i, arr[]. n - def heapify(arr, n, i): largest = i # Initialize largest as root l = 2 * i + 1 # left = 2*i + 1 r = 2 * i + 2 # right = 2*i + 2 # , if l < n and arr[i] < arr[l]: largest = l # , if r < n and arr[largest] < arr[r]: largest = r # , if largest != i: arr[i],arr[largest] = arr[largest],arr[i] # # heapify . heapify(arr, n, largest) # def heapSort(arr): n = len(arr) # max-heap. for i in range(n, -1, -1): heapify(arr, n, i) # for i in range(n-1, 0, -1): arr[i], arr[0] = arr[0], arr[i] # heapify(arr, i, 0) # arr = [ 12, 11, 13, 5, 6, 7] heapSort(arr) n = len(arr) print ("Sorted array is") for i in range(n): print ("%d" %arr[i]), # Mohit Kumra
C锐
// C# using System; public class HeapSort { public void sort(int[] arr) { int n = arr.Length; // ( ) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // for (int i=n-1; i>=0; i--) { // int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // heapify heapify(arr, i, 0); } } // i, // arr[]. n - void heapify(int[] arr, int n, int i) { int largest = i; // int l = 2*i + 1; // left = 2*i + 1 int r = 2*i + 2; // right = 2*i + 2 // if (l < n && arr[l] > arr[largest]) largest = l; // , if (r < n && arr[r] > arr[largest]) largest = r; // if (largest != i) { int swap = arr[i]; arr[i] = arr[largest]; arr[largest] = swap; // heapify(arr, n, largest); } } /* n */ static void printArray(int[] arr) { int n = arr.Length; for (int i=0; i<n; ++i) Console.Write(arr[i]+" "); Console.Read(); } // public static void Main() { int[] arr = {12, 11, 13, 5, 6, 7}; int n = arr.Length; HeapSort ob = new HeapSort(); ob.sort(arr); Console.WriteLine("Sorted array is"); printArray(arr); } } // // Akanksha Ra (Abby_akku)
p
<?php // Php // i, // arr[]. n - function heapify(&$arr, $n, $i) { $largest = $i; // $l = 2*$i + 1; // = 2*i + 1 $r = 2*$i + 2; // = 2*i + 2 // if ($l < $n && $arr[$l] > $arr[$largest]) $largest = $l; // , if ($r < $n && $arr[$r] > $arr[$largest]) $largest = $r; // if ($largest != $i) { $swap = $arr[$i]; $arr[$i] = $arr[$largest]; $arr[$largest] = $swap; // heapify($arr, $n, $largest); } } // , function heapSort(&$arr, $n) { // ( ) for ($i = $n / 2 - 1; $i >= 0; $i--) heapify($arr, $n, $i); // for ($i = $n-1; $i >= 0; $i--) { // $temp = $arr[0]; $arr[0] = $arr[$i]; $arr[$i] = $temp; // heapify heapify($arr, $i, 0); } } /* n */ function printArray(&$arr, $n) { for ($i = 0; $i < $n; ++$i) echo ($arr[$i]." ") ; } // $arr = array(12, 11, 13, 5, 6, 7); $n = sizeof($arr)/sizeof($arr[0]); heapSort($arr, $n); echo 'Sorted array is ' . "\n"; printArray($arr , $n); // Shivi_Aggarwal ?>
结论:
: 5 6 7 11 12 13
这是以前的C代码供参考。
备注:
金字塔形排序是一种非常合适的算法。 它的典型实现方式不稳定,但是可以照此完成(请参阅此处 )。
时间复杂度: heapify 的时间复杂度为O(登录)。 createAndBuildHeap()的时间复杂度为O(n),金字塔排序的总运行时间为O(nLogn)。
金字塔形排序应用程序:
- 对几乎排序(或按K个位置排序)的数组进行排序 ;
- 数组中的k个最大(或最小)元素 。
金字塔排序算法的使用受到限制,因为Quicksort和Mergesort在实践中更好。 但是,堆数据结构本身经常被使用。 请参阅堆数据结构应用程序
屏幕截图:
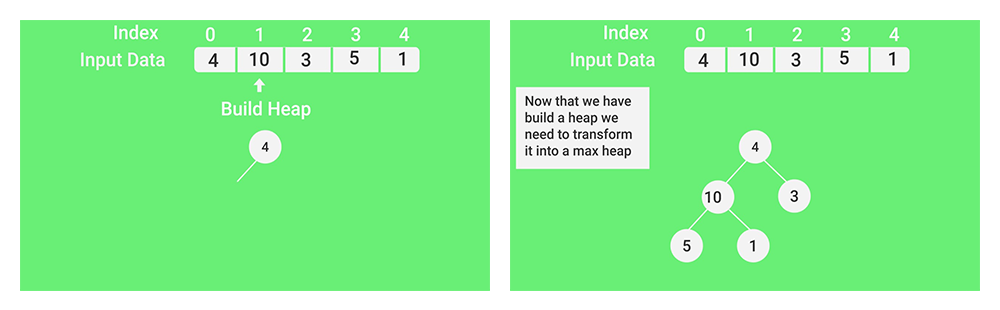
-(现在我们已经建立了堆,我们需要将其转换为max-heap)

-(在最大堆中,父节点始终大于或等于子节点
10比4多。因此,我们交换4和10)
-(在最大堆中,父节点始终大于或等于子节点
另外5个4.因此,我们交换位置5和4)

-(交换第一个和最后一个节点,并从堆中删除最后一个节点)
金字塔测试
GeeksforGeeks / GeeksQuiz上的其他排序算法:
快速排序 , 按选择排序 , 气泡排序 , 插入排序 , 合并排序 , 金字塔排序 , 位排序 , 计数排序 , 块排序 , 壳 排序,梳状排序,计数 与列表排序 。
分拣车间
如果您发现有问题或想要分享有关上述主题的其他信息,请发表评论。