讲座课程“数字信号处理基础”

大家好！

人们经常向我询问有关数字信号处理（DSP）领域的任务的问题。 我详细介绍了细微差别，提出了必要的信息来源。 但是，正如时间所表明的那样，所有听众在学习这一领域的过程中都缺乏实际的任务和例子。 在这方面，我决定编写有关数字信号处理的简短交互式课程，并将其放在公共领域 。

大部分用于视觉和交互式演示的培训材料都是使用Jupyter Notebook实现的。 假定读者具有高等数学领域的基础知识，并且对Python编程语言有一点了解。

讲座清单

本课程包含有关数字信号处理领域各种主题的演讲形式。 使用Python库（numpy，scipy，matplotlib包等）展示材料。 本课程的基本信息取材自我的演讲，我作为研究生向莫斯科能源学院（NRU MEI）的学生提供了这些演讲。 这些演讲的部分信息在我担任讲师的当代电子中心的培训研讨会上使用。 此外，该材料还包括翻译各种科学文章，汇编可靠信息和有关数字信号处理的文献中的信息，以及有关应用程序包和Python scipy和numpy库的内置函数的官方文档。

对于MATLAB（GNU Octave）用户，从程序代码的角度掌握材料并不困难，因为主要功能及其属性在很大程度上与Python库中的方法相同且相似。

所有材料均按数字信号处理的主要主题分组：

1. 信号：模拟，离散，数字。 Z转换
2. 傅立叶变换：幅度和相位信号，DFT和FFT，
3. 卷积和相关。 线性和循环卷积。 快速卷积
4. 随机过程。 白噪声。 概率密度函数
5. 确定性信号。 调制方式：AM，FM，FM，LFM。 操纵
6. 信号滤波：IIR，FIR滤波器
7. 窗口在过滤任务中起作用。 检测弱信号。
8. 重采样：抽取和内插。 CIC滤波器，移动平均滤波器

讲座列表足够多， 但是对于DSP领域的入门者来说当然是不完整的。 我计划在空闲时间支持和开发该项目。

在哪里找到？

所有资料都是绝对免费的 ，可以作为我的github上的开放源代码作为一个开放源代码项目获得 。 资料以两种格式呈现-用于交互工作，学习和编辑的Jupyter Notebook形式，以及从这些笔记本编译的HTML文件的形式（从github下载后，它们具有非常适合阅读和打印的格式）。

以下是对课程各部分的简短说明，并附有简短的说明，术语和定义。 最初的讲座中提供了基本信息，这里只是简要概述！

信号。 Z转换

简介部分，其中包含有关信号类型的基本信息。 介绍了离散序列，delta函数和Heaviside函数（单位跳跃）的概念。

根据信号集呈现方法的不同，所有信号可分为四类：

• 模拟-由时间上连续的功能描述，
• 离散-通过采样指定的步骤及时中断，
• 量化-具有一组有限的水平（通常为振幅），
• 数字-离散信号和量化信号的属性的组合。

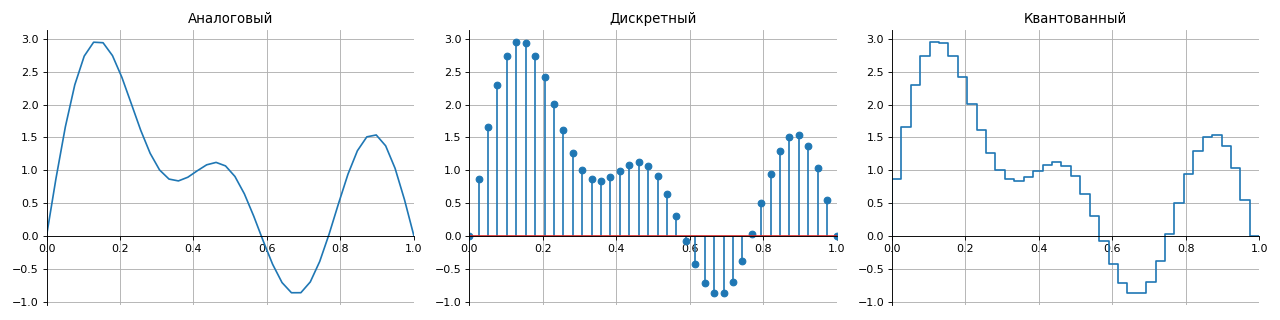
为了从数字信号正确重建模拟信号而没有失真和损失，使用了称为Kotelnikov（奈奎斯特-香农）定理的采样定理。

具有有限频谱的任何连续信号都可以唯一地恢复，而不会因其离散采样而损失，该离散采样的频率严格大于连续信号频谱上限频率的两倍。

只要时间的连续函数占用从0到上限频率的频带，这种解释就是有效的。 如果错误地选择了量化和离散步骤，则信号将从模拟失真变为离散失真。

同样在本节中，描述了Z变换及其属性，并显示了Z形式的离散序列的表示形式。

有限离散序列的示例：

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} 

。
Z形式的相同序列的示例：

X（z）= 2 + z -1-2z ^-2 + 2z ^-4 + 3z ^-5 + 1z ^-6

傅立叶变换。 物产 DFT和FFT

本节介绍信号的时域和频域的概念。 介绍了离散傅里叶变换（DFT）的定义。 考虑了直接和逆DFT及其主要属性。 显示的是从DFT到基数2的快速傅立叶变换（FFT）算法的转换（频率和时间的抽取算法）。 反映了FFT与DFT相比的有效性。

特别是，本节介绍了Python包scipy.ffpack，用于计算各种傅立叶变换（正弦，余弦，正弦，逆向，多维，实数）。

傅立叶变换使您可以将任何函数表示为一组谐波信号！ 傅里叶变换是卷积方法和数字相关器设计的基础，被积极地用于频谱分析中，并在处理长整数时使用。

离散信号频谱的特征：
1.离散信号的频谱密度是周期函数，周期等于采样频率。
2.如果离散序列为实数 ，则该序列的频谱密度模量为偶函数，自变量为奇数频率函数。

谐波信号频谱：

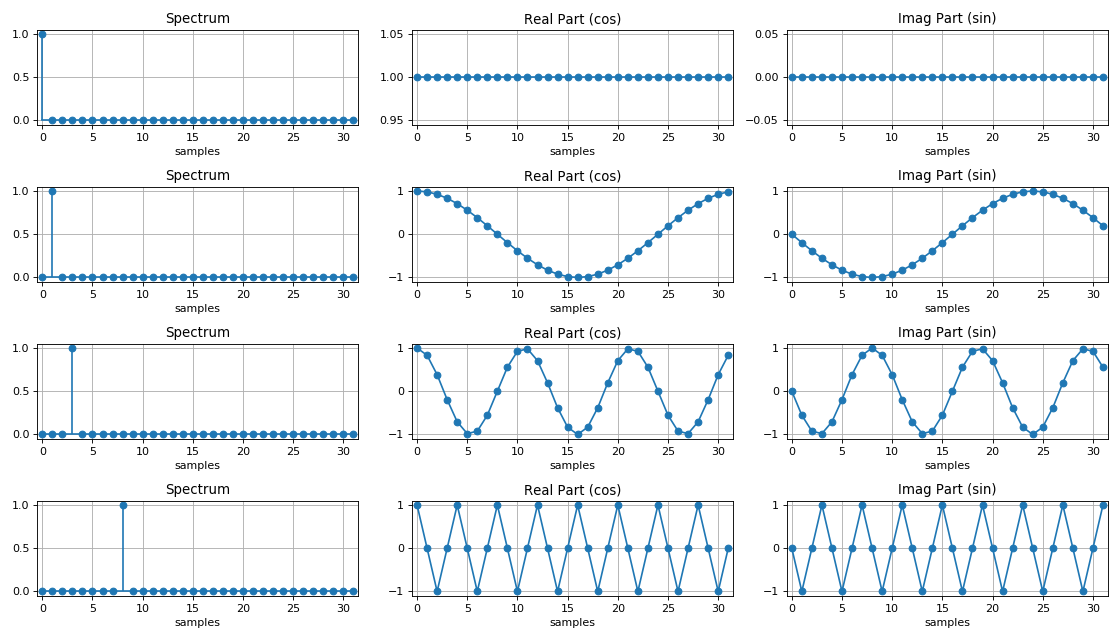
DFT和FFT的功效比较

FFT算法的效率和线性执行的操作数取决于序列长度N：


如您所见，转换时间越长，在计算资源（就处理速度或硬件单元数量而言）方面的节省就越大！

任何任意波形都可以表示为一组不同频率的谐波信号。 换句话说，时域中形状复杂的信号在频域中具有一组复杂样本，称为*谐波*。 这些样本表示特定频率下谐波效应的幅度和相位。 频域中的谐波组越大，复杂波形出现的越准确。

卷积与相关

本节介绍离散随机和确定性序列的相关和卷积概念。 示出了具有卷积的自相关函数和互相关函数之间的关系。 描述了卷积的性质，特别是考虑了离散信号的线性和循环卷积方法，并以离散序列为例进行了详细分析。 此外，显示了一种使用FFT算法计算“快速”卷积的方法。

在实际问题中，通常会提出一个过程与另一个过程的相似程度或一个过程与另一个过程之间的独立性的问题。 换句话说，需要确定信号之间的关系，即找到相关性 。 相关方法用于各种任务：信号搜索，计算机视觉和图像处理，雷达问题中，以确定目标的特性并确定距物体的距离。 另外，相关性用于搜索噪声中的微弱信号。

卷积描述了信号之间的相互作用。 如果信号之一是滤波器的脉冲响应，则输入序列与脉冲响应的卷积只是电路对输入动作的反应。 换句话说，所得信号反映了信号通过滤波器的通道。

自相关函数 （ACF）用于编码信息。 根据长度，频率和形状的参数来选择编码序列很大程度上是由于该序列的相关特性。 最佳代码序列的错误检测或操作（用于检测信号，阈值设备）或错误同步（用于发送和接收代码序列）的可能性最低。

本节提供了一个表格，比较了快速卷积和通过直接公式计算的卷积（通过实数乘法）的有效性。

如您所见，对于FFT长度最大为64的情况，快速卷积会丢失直接方法。 但是，随着FFT长度的增加，结果朝相反的方向变化-快速卷积开始优于直接方法。 显然，FFT越长，频率法的增益就越好。

随机信号和噪声

在本节中，介绍了随机信号，概率密度和随机分布定律的概念。 考虑数学矩-均值（数学期望）和方差（或该数量的根是标准偏差）。 同样在本节中，正态分布和白噪声的相关概念也被认为是信号处理过程中的主要噪声源（干扰）。

随机信号是时间的函数，其值事先未知，只能以一定概率预测。 随机信号的主要特征包括：

• 分布规律（信号值在一定间隔内的相对停留时间），
• 信号功率的频谱分布。

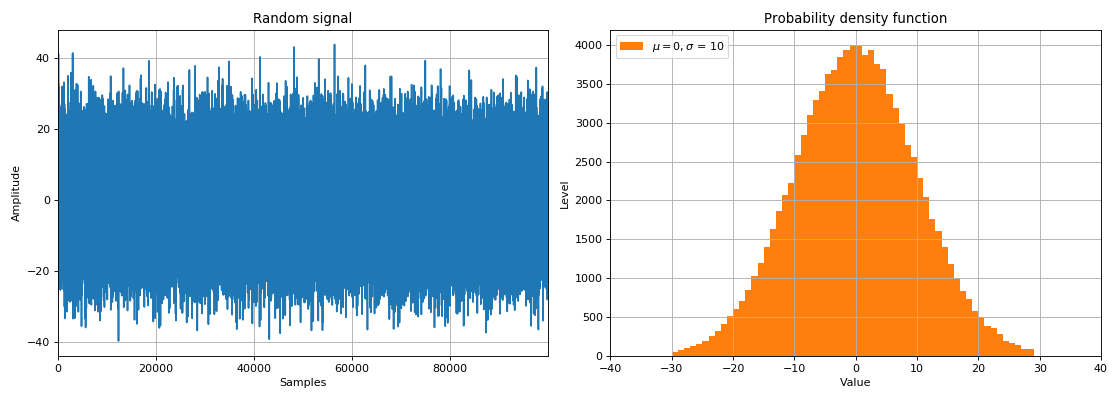
在DSP任务中，随机信号分为两类：

• 噪声-由一组不同的频率和幅度组成的随机波动，
• 载有信息的信号，对此进行处理必须采用概率方法。

使用随机变量，我们可以模拟真实介质对信号从源到数据接收器的传递的影响。 当信号通过一些嘈杂的链路时，所谓的白噪声会添加到信号中。 通常，这种噪声的频谱密度在所有频率上均等（均匀）分布，并且时域中的噪声值呈正态分布（高斯分布定律）。 由于在选定的时间样本中将白噪声物理地添加到信号幅度中，因此将其称为加性高斯白噪声（AWGN）。

信号，调制和操纵

本节介绍了更改谐波信号的一个或多个参数的基本方法。 介绍了幅度，频率和相位调制的概念。 特别强调了雷达问题中使用的线性频率调制。 显示了信号的主要特征，即取决于调制参数的已调制信号的频谱。



为了方便起见，已在Python中创建了一组实现上述调制类型的函数。 线性调频信号实现示例：

 def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs): """ Create Chirp signal Parameters ---------- amp : float Signal magnitude beta : float Modulation bandwidth: beta < N for complex, beta < 0.5N for real freq : float or int Linear frequency of signal period : integer Number of points for signal (same as period) kwargs : bool Complex signal if is_complex = True Modulated by half-sine wave if is_modsine = True """ is_complex = kwargs.get('is_complex', False) is_modsine = kwargs.get('is_modsine', False) t = np.linspace(0, 1, period) tt = np.pi * (freq * t + beta * t ** 2) if is_complex is True: res = amp * (np.cos(tt) + 1j * np.sin(tt)) else: res = amp * np.cos(tt) if is_modsine is True: return res * np.sin(np.pi * t) return res 

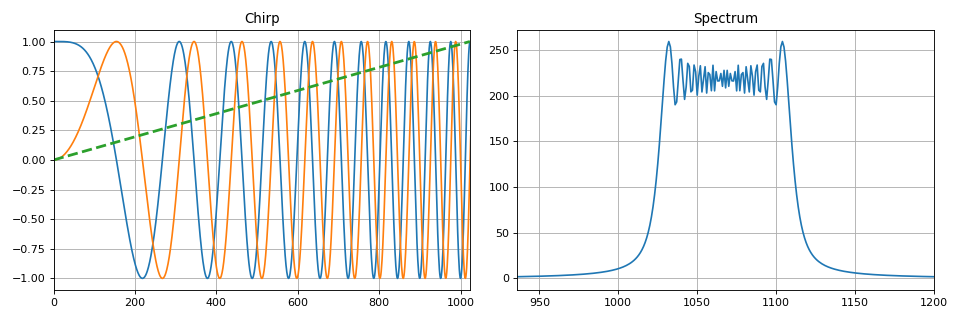
同样在本节中，根据离散消息的传输理论，描述了数字调制的类型-操作。 与模拟信号一样，数字谐波序列可以在幅度，相位和频率（或同时几个参数）上进行操作。

数字滤波器-IIR和FIR

足够大的部分专门用于离散序列的数字滤波。 在数字信号处理任务中，数据流经称为滤波器的电路。 数字滤波器与模拟滤波器一样，具有不同的特性-频率：频率响应，相位响应，时间：脉冲响应以及滤波器的传输特性。 数字滤波器主要用于提高信号质量-将信号与数据序列隔离，或降低不需要的信号-抑制输入采样序列中的某些信号。



本节列出了数字滤波器（与模拟滤波器相比）的主要优缺点。 介绍了滤波器的脉冲和传递特性的概念。 考虑了两类滤波器-具有无限脉冲响应（IIR）和有限脉冲响应（FIR）。 显示了一种以规范和直接形式设计过滤器的方法。 对于FIR滤波器，考虑了如何切换到递归形式的问题。



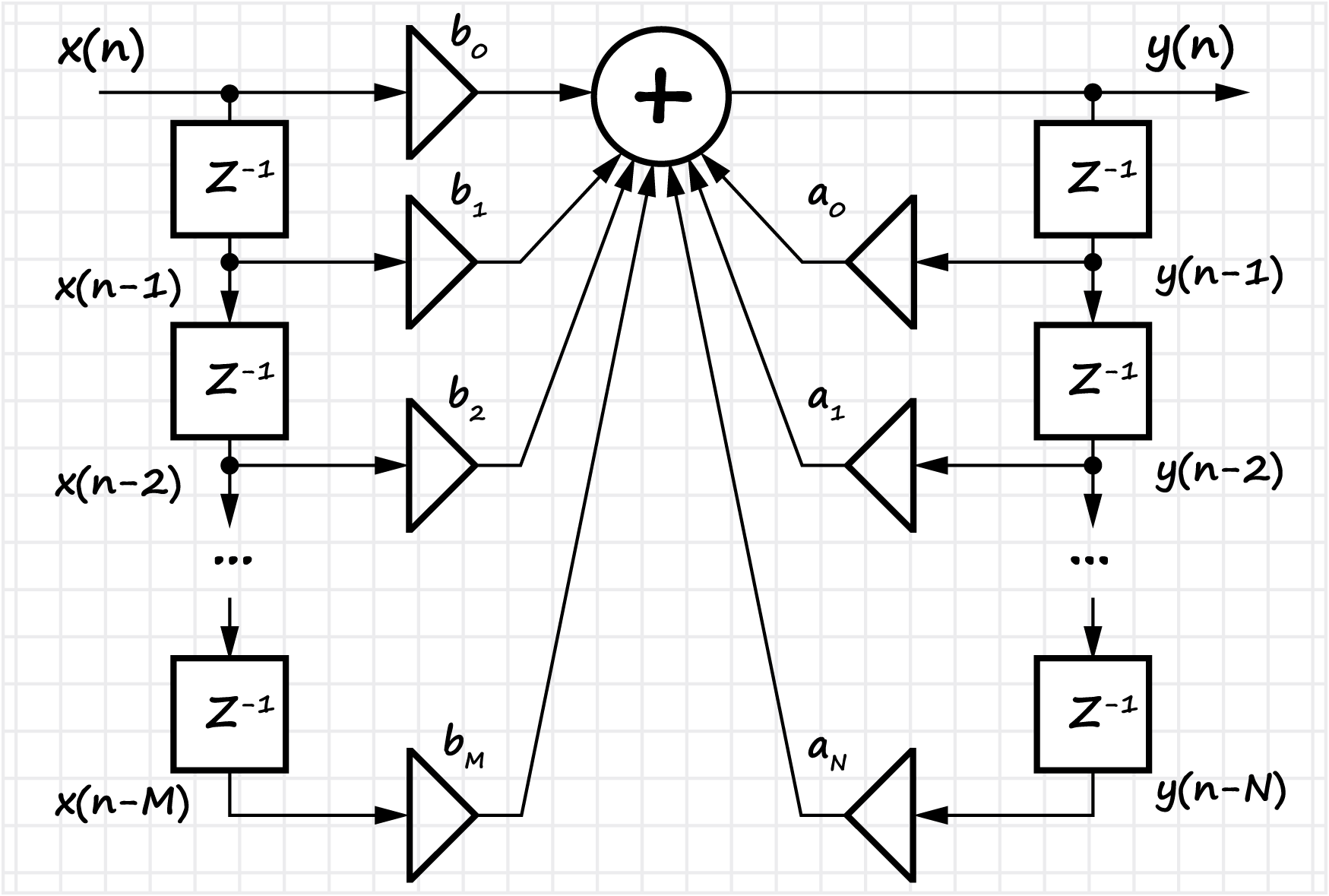
对于FIR滤波器，从技术规范的开发阶段（标明主要参数）到软件和硬件的实现-滤波器系数的搜索（考虑到数字，位深等的表示形式）显示了滤波器的设计过程。 介绍了对称FIR滤波器的定义，线性相位响应及其与群时延概念的关系。

过滤任务中的窗口功能

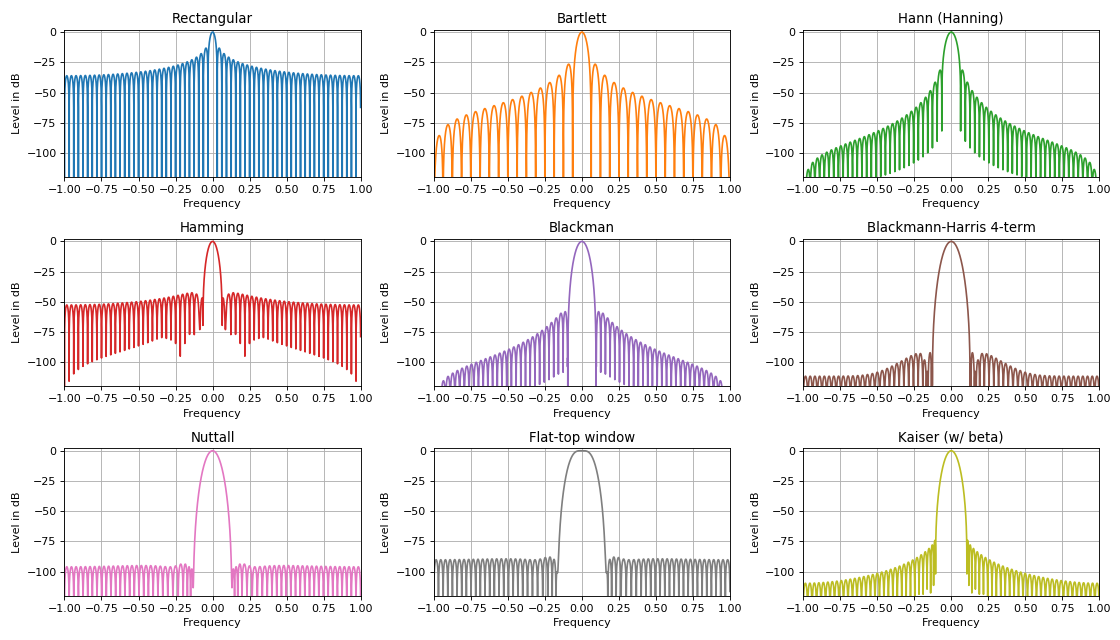
在数字信号处理任务中，使用了各种形状的窗函数，当它们在时域中叠加到信号上时，可以定性地改善其频谱特性。 大量的各种窗口主要是由于任何窗口覆盖的主要功能之一。 该特征通过旁瓣的水平与中央瓣的宽度之间的关系来表达。 规则：

频谱旁瓣的抑制能力越强，频谱的主瓣越宽，反之亦然。

窗口功能的应用之一：通过抑制旁瓣电平，在较强信号的背景下检测弱信号。 DSP任务中的主要窗口功能是**三角形，正弦曲线，Lanczos，Hann，Hamming，Blackman，Harris，Blackman-Harris窗口，平顶窗口，Natall，Gauss，Kaiser窗口**等。 它们中的大多数通过对具有特定权重的谐波信号求和而通过有限级数表示。 实际上，此类信号可以在任何硬件设备（可编程逻辑电路或信号处理器）上完美实现。

重采样。 抽取和插值

本节讨论多速信号处理的问题-采样频率的变化。 信号的多速处理（多速率处理）表明，在数字信号的线性转换过程中，可以沿减少或增加的方向或分数倍的方向更改采样频率。 这将导致更高效的信号处理，因为它开辟了使用最小允许采样频率的可能性，从而大大降低了设计数字系统所需的计算性能。

抽取 （抽取）-下采样。 插值 -增加采样率。

本节还考虑了同类FIR滤波器的类别，它们称为积分梳状滤波器（CIC，级联积分器-梳状）。 显示了CIC滤波器的实现，基本属性和功能。 由于CIC滤波器中发生的数学运算具有线性关系，因此有可能将多个滤波器连续级联，这会成比例地降低旁瓣电平，但也会增加幅度-频率特性主瓣的“阻塞”。



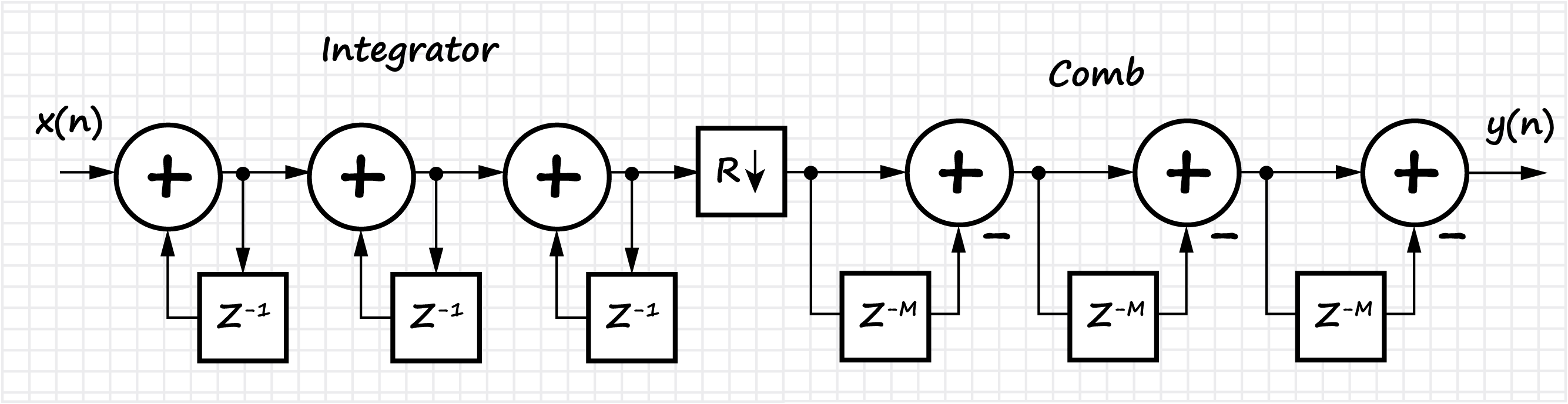
取决于抽取系数的滤波器频率响应图：



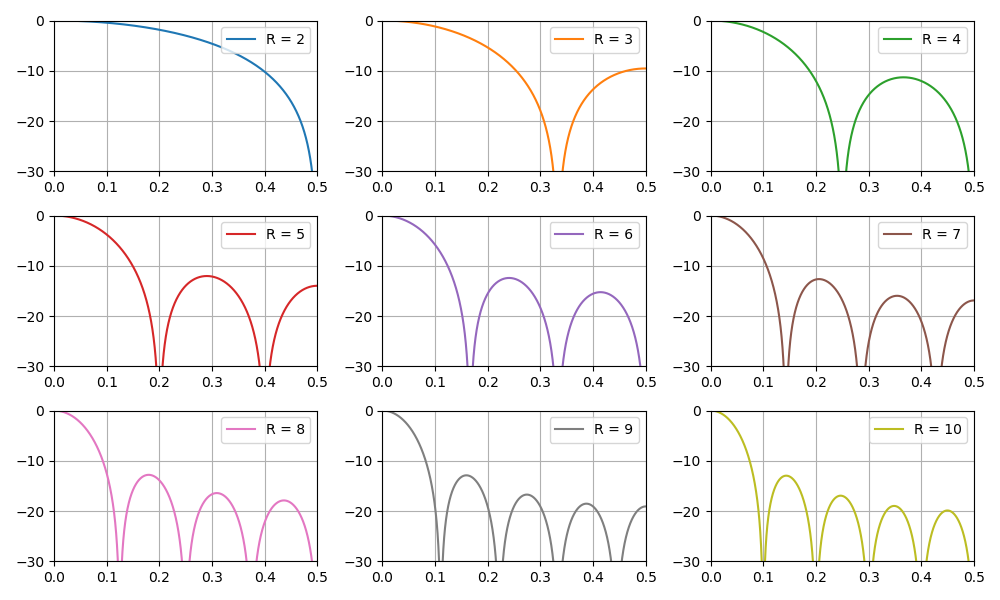
在本节中，我们还将讨论根据CIC滤波器的参数增加数据位深的问题。 这在软件实现任务中尤其重要，特别是在FPGA上。

为了在Python中实际实现CIC过滤器， 已经开发了一个单独的类CicFilter ，该类实现了抽取和插值方法。 还显示了使用scipy Python软件包中的内置方法进行的采样率更改。





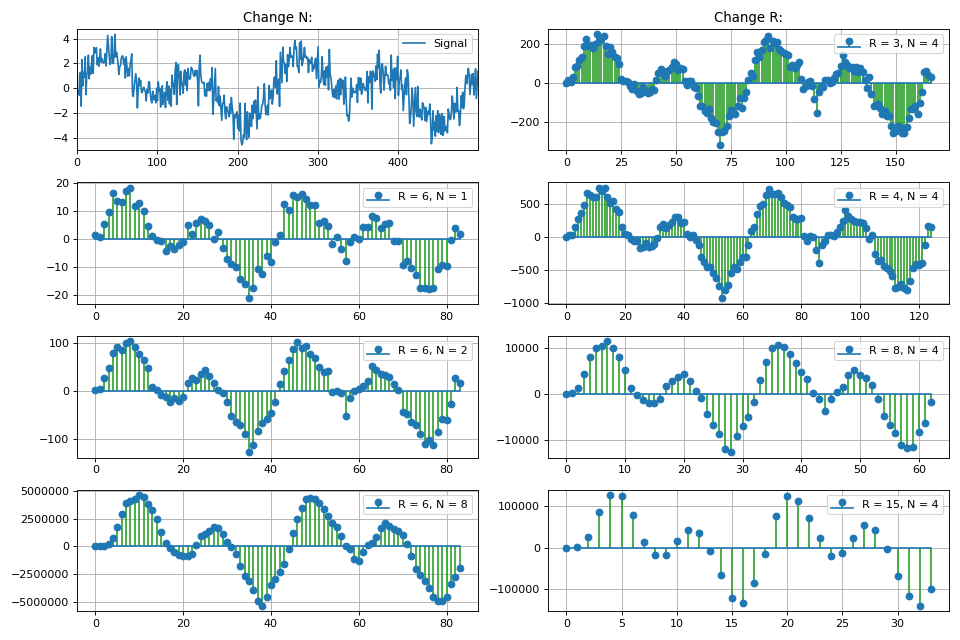
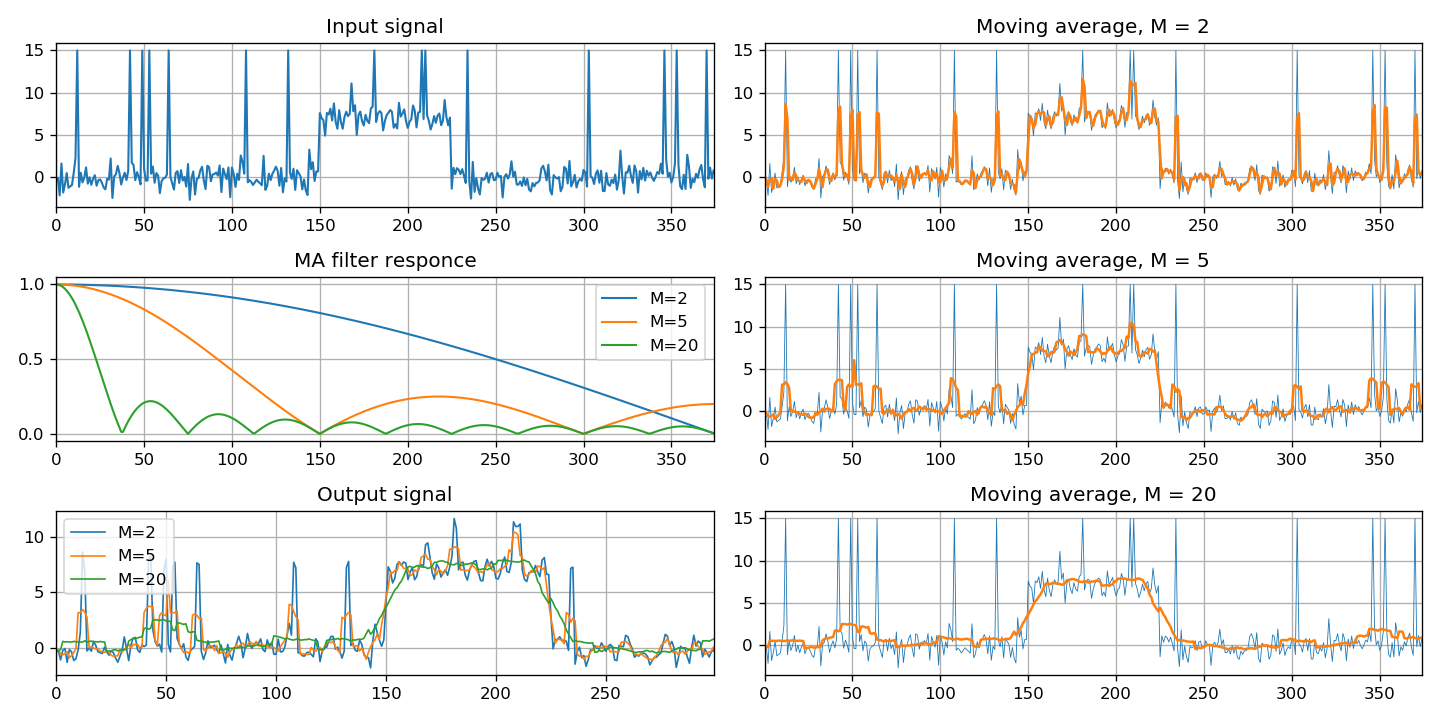
最后，本节提供一类特殊的过滤器-移动平均线。 展示了三种实现方法：通过使用FIR滤波器和IIR滤波器对信号进行卷积。

结论

我希望本讲课课程与我以前有关数字FPGA信号处理的文章结合起来，将带来实际的好处，并帮助读者更好地理解数字信号处理的基础。 该项目将得到改进，并补充新的有用且有趣的材料。 跟随发展！

除了本材料之外，我还在主要的DSP模块（使用Python）上支持和开发我的项目 。 它包含一个用于生成各种信号的程序包，一类用于抽取和插值问题的CIC滤波器，一种用于计算校正FIR滤波器的系数的算法，一个移动平均滤波器，一种用于通过二维转换方法计算超长FFT的算法（后者在与FPGA上的硬件实现一起使用时非常有用） 。

感谢您的关注！