为什么下一篇关于如何从头开始编写神经网络的文章? las,我找不到从头到尾都能描述其理论和代码的文章。 我立即警告说,将会有很多数学。 我假设读者熟悉线性代数,偏导数的知识,至少部分地熟悉概率论,以及Python和Numpy。 我们将处理一个完全连接的神经网络和MNIST。
数学 第1部分(简单)
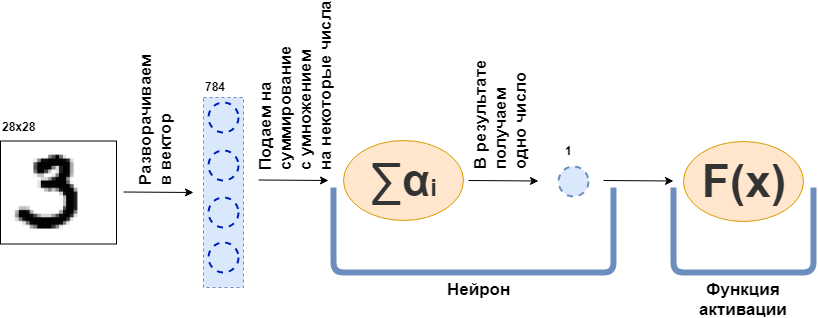
什么是全连接层(FC层)? 通常,他们说类似“完全连接的层是一层,每个神经元连接到上一层的所有神经元”之类的东西。 尚不清楚什么是神经元,它们如何连接,尤其是在代码中。 现在,我将尝试通过一个例子来解析它。 设一层100个神经元。 我知道我还没有解释它的含义,但让我们想象一下,有100个神经元,它们有一个输入,数据被发送,一个输出,它们从中提供数据。 然后,将28x28像素的黑白图片馈送到输入-如果将其拉伸为矢量,则只有784个值。 图片可以称为输入层。 然后,对于100个神经元中的每个与每个“神经元”或(如果您愿意)上一层(即图片)的值进行连接,则100个神经元中的每个必须接受原始图片的784个值。 例如,对于100个神经元中的每一个,将图片的784个值乘以784个数字并将它们相加就足够了,结果就是一个数字出来了。 也就是说,这是一个神经元:
$$ display $$ \文字{Neuron输出} = \文字{一些数字} _ {1} \ cdot \文字{图片值} _1〜+ \\ +〜...〜+〜\文字{some-该数字} _ {784} \ cdot \文字{图片值} _ {784} $$显示$$
然后证明每个神经元有784个数,而所有这些数为:(此层上的神经元数)x(上一层上的神经元数)=
$内联$ 100 \次784 $内联$ = 78,400位数。 这些数字通常称为图层权重。 每个神经元都会给出其数目,因此我们得到一个100维向量,实际上,我们可以写成通过将784维向量(我们的原始图像)乘以一个大小权重矩阵获得此100维向量
$内联$ 100 \次784 $内联$ :
$$显示$$ \ \粗体符号{x} ^ {100} = W_ {100 \ times784} \ cdot \粗体符号{x} ^ {784} $$显示$$
此外,将所得的100个数字传递给激活函数(一些非线性函数),该函数分别影响每个数字。 例如,S形,双曲正切,ReLU等。 激活函数必然是非线性的,否则神经网络将仅学习简单的变换。
然后,将结果数据再次馈送到具有不同数量神经元的完全连接层,并再次馈送到激活功能。 这会发生几次。 网络的最后一层是产生答案的层。 在这种情况下,答案是有关图片中编号的信息。
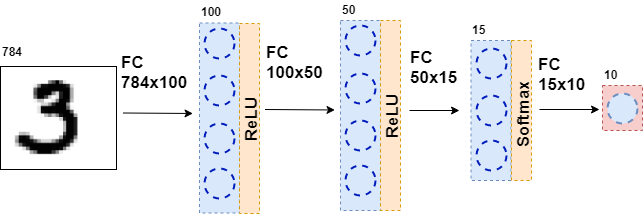
在网络训练期间,有必要知道图片中显示了什么图形。 也就是说,数据集被标记。 然后,您可以使用另一个元素-错误函数。 她查看了神经网络的响应,并将其与实际答案进行了比较。 因此,神经网络正在学习。
问题的一般说明
整个数据集是一个大张量(我们将多维数据数组称为张量)
$ inline $ \ boldsymbol {X} = \左[\ boldsymbol {x} _1,\ boldsymbol {x} _2,\ ldots,\ boldsymbol {x} _n \ right] $ inline $ 在哪里
$ inline $ \ boldsymbol {x} _i $ inline $ -第i个对象,例如图片,它也是张量。 每个对象都有
$内联$ y_i $内联$ -第i个对象的正确答案。 在这种情况下,神经网络可以表示为一些函数,该函数将对象作为输入并给出一些答案:
$$显示$$ F(\粗体符号{x} _i)= \帽子{y} _i $$显示$$
现在让我们仔细看看该功能
$内联$ F(\粗体符号{x} _i)$内联$ 。 由于神经网络由图层组成,因此每个单独的图层都是一个函数。 这意味着
$$ display $$ F(\\粗体符号{x} _i)= f_k(f_ {k-1}(\ ldots(f_1(\粗体符号{x} _i))))= \ hat {y} _i $$ display $ $
也就是说,在第一个功能(第一层)中,以某种张量的形式呈现图片。 功能介绍
$内联$ f_1 $内联$ 给出一些答案-也是张量,但是尺寸不同。 该张量将称为内部表示。 现在,此内部表示被馈送到函数的输入
$内联$ f_2 $内联$ ,并给出其内部表示。 依此类推,直到功能
$内联$ f_k $内联$ -最后一层-不会给出答案
$ inline $ \ hat {y} _i $ inline $ 。
现在,任务是训练网络-使网络答案与正确答案匹配。 首先,您需要测量神经网络的错误程度。 测量这是一个误差函数。
$ inline $ L(\ hat {y} _i,y_i)$ inline $ 。 我们施加了限制:
1。
$ inline $ \ hat {y} _i \ xrightarrow {} y_i \ Rightarrow L(\ hat {y} _i,y_i)\ xrightarrow {} 0 $ inline $
2。
$ inline $ \存在〜dL(\ hat {y} _i,y_i)$ inline $
3。
$ inline $ L(\ hat {y} _i,y_i)\ geq 0 $ inline $
限制2应用于层的所有功能
$内联$ f_j $内联$ -让他们都与众不同。
而且,实际上(我没有提到),其中一些功能取决于参数-神经网络的权重-
$内联$ f_j(\粗体{x} _i | \粗体{\ omega} _j)$内联$ 。 整个想法是捡起这样的重量
$ inline $ \ hat {y} _i $ inline $ 恰好与
$内联$ y_i $内联$ 在数据集的所有对象上。 我注意到并非所有功能都有权重。
那么我们在哪里停了下来? 神经网络的所有函数都是可微的,误差函数也是可微的。 回忆一下渐变的特性之一-显示函数的增长方向。 我们使用限制1和限制3,
$$ display $$ L(F(\(\粗体符号{x} _i)))= L(f_k(f_ {k-1}(\ ldots(f_1(\粗体符号{x} _i)))))= L(\ hat {y} _i)$$显示$$
我可以考虑偏导数和复杂函数的导数。 现在,您拥有了计算所需的一切
$$显示$$ \ frac {\部分L(F(\(粗体符号{x} _i))}} {\部分\粗体符号{\ omega_j}} $$显示$$
对于任何i和j。 该偏导数显示了变化的方向
$ inline $ \ boldsymbol {\ omega_j} $ inline $ 放大
$内联$ L $内联$ 。 为了减少您需要采取一步
$ inline $-\ frac {\部分L(F(\(boldsymbol {x} _i)))} {\部分\ boldsymbol {\ omega_j}} $ inline $ 没有什么复杂的。
因此,训练网络的过程构造如下:在一个循环中,我们多次遍历整个数据集(这称为一个时代),对于我们考虑的每个数据集对象
$ inline $ L(\ hat {y} _i,y_i)$ inline $ (这称为正向传递)并考虑偏导数
$内联$ \部分L $内联$ 所有重量
$ inline $ \ boldsymbol {\ omega_j} $ inline $ ,然后更新权重(这称为反向传递)。
我注意到我尚未介绍任何特定的功能和层。 如果在此阶段尚不清楚该如何处理,我建议继续阅读-将会有更多的数学,但现在将与示例一起使用。
数学 第2部分(困难)
错误功能
我将从头开始,并得出分类问题的误差函数。 对于回归问题,误差函数的推导在《深度学习》一书中有很好的描述。 沉浸在神经网络的世界中。”
为简单起见,有一个将猫照片和狗照片分开的神经网络(NN),并且有一组猫狗的照片有正确答案
$ inline $ y_ {true} $ inline $ 。
$$显示$$ NN(图片| \ Omega)= y_ {pred} $$显示$$
我接下来要做的一切与最大似然法非常相似。 因此,主要任务是找到似然函数。 如果我们省略细节,那么这种将神经网络的预测与正确答案进行比较的函数,如果它们重合,则将具有很大的价值,反之亦然。 使用给定的参数可以想到正确答案的可能性:
$$显示$$ p(y_ {pred} = y_ {true} | \ Omega)$$显示$$
现在,我们将进行一些伪装,似乎并非随处可见。 让神经网络以二维向量的形式给出答案,该向量的值之和为1.此向量的第一个元素可以称为猫在照片中的置信度,而第二个元素称为狗在照片中的置信度。 是的,几乎是概率!
$$显示$$ NN(图片| \ Omega)= \左[\开始{矩阵} p_0 \\ p_1 \\\结束{矩阵} \右] $$显示$$
现在,似然函数可以重写为:
$$ display $$ p(y_ {pred} = y_ {true} | \ Omega)= p_ \ Omega(y_ {pred})^ t_ {0} *(1-p_ \ Omega(y_ {pred}))^ t_ {1} = \\ p_0 ^ {t_0} * p_1 ^ {t_1} $$显示$$
哪里
$ inline $ t_0,t_1 $ inline $ 正确类别的标签,例如,如果
$ inline $ y_ {true} = cat $ inline $ 然后
$内联$ t_0 == 1,t_1 == 0 $内联$ 如果
$ inline $ y_ {true} =狗$ inline $ 然后
$内联$ t_0 == 0,t_1 == 1 $内联$ 。 因此,始终考虑应该由神经网络预测(但不一定由神经网络预测)的类的概率。 现在可以将其概括为任意数量的类(例如,m个类):
$$ display $$ p(y_ {pred} = y_ {true} | \ Omega)= \ prod_0 ^ m p_i ^ {t_i} $$ display $$
但是,在任何数据集中都有许多对象(例如N个对象)。 我希望神经网络对每个或大多数对象给出正确的答案。 为此,您需要将数据集中每个对象的上述公式的结果相乘。
$$ display $$ MaximumLikelyhood = \ prod_ {j = 0} ^ N \ prod_ {i = 0} ^ m p_ {i,j} ^ {t_ {i,j}} $$ display $$
为了获得良好的结果,此功能需要最大化。 但是,首先,将梯度减小到最小是困难的,因为我们有一个随机的梯度下降和所有的包子-仅分配一个负号,其次,很难完成大量工作-它是对数。
$$ display $$ CrossEntropyLoss =-\总和\限制_ {j = 0} ^ {N} \总和\限制_ {i = 0} ^ {m} t_ {i,j} \ cdot \ log(p_ {i,j })$$显示$$
太好了! 结果是交叉熵,或者在二元情况下为对数损失。 此函数易于计数,甚至易于区分:
$$显示$$ \ frac {\部分CrossEntropyLoss} {\部分p_j} =-\ frac {\ boldsymbol {t_j}} {\ boldsymbol {p_ {j}}} $$显示$$
您需要针对反向传播算法进行区分。 我注意到误差函数不会改变向量的尺寸。 如果像MNIST的情况那样,输出是答案的10维向量,那么在计算导数时,我们将得到导数的10维向量。 另一个有趣的事情是,导数中只有一个元素不会为零,此时
$内联$ t_ {i,j} \ neq 0 $内联$ ,即答案正确。 而且,神经网络在给定对象上预测出正确答案的可能性越小,误差函数将越多。
激活功能
在神经网络的每个完全连接层的输出处,必须存在非线性激活函数。 没有它,就不可能训练出有意义的神经网络。 展望未来,神经网络的完全连接层只是将输入数据与权重矩阵相乘。 在线性代数中,这称为线性映射-线性函数。 线性函数的组合也是线性函数。 但这意味着这样的函数只能近似线性函数。 las,这不是为什么需要神经网络的原因。
软最大
通常将此功能用于网络的最后一层,因为它将最后一层的向量转换为“概率”向量:向量的每个元素从0到1且其和为1。它不会改变向量的维数。
$$ display $$ Softmax_i = \ frac {e ^ {x_i}} {\ sum \ limits_ {j} e ^ {x_j}} $$ display $$
现在让我们继续进行派生搜索。 由于
$ inline $ \ boldsymbol {x} $ inline $ 是一个向量,其所有元素始终存在于分母中,那么当采用导数时,我们得到雅可比矩阵:
$$ display $$ J_ {Softmax} = \开始{cases} x_i-x_i \ cdot x_j,i = j \\-x_i \ cdot x_j,i \ neq j \ end {cases} $$ display $$
现在关于反向传播。 导数向量来自上一层(通常这是一个误差函数)
$ inline $ \ boldsymbol {dz} $ inline $ 。 万一
$ inline $ \ boldsymbol {dz} $ inline $ 来自mnist的错误函数
$ inline $ \ boldsymbol {dz} $ inline $ -10维向量。 然后,雅可比矩阵的尺寸为10x10。 得到
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ ,它会延伸到上一层(请记住,当错误传播回来时,我们会从网络的末端到网络的起点),我们需要乘以
$ inline $ \ boldsymbol {dz} $ inline $ 在
$ inline $ J_ {Softmax} $ inline $ (每列行):
$$ display $$ dz_ {new} = \粗体符号{dz} \倍J_ {Softmax} $$ display $$
在输出中,我们得到一个10维导数向量
$ inline $ \ boldsymbol {dz_ {new}} $ inline $ 。
露露
$$显示$$ ReLU(x)= \开始{cases} x,x> 0 \\ 0,x <0 \ end {cases} $$ display $$
ReLU在2011年发表“深度稀疏整流器神经网络”一文后开始被广泛使用。 但是,这种功能以前是已知的。 “激活能力”的概念适用于ReLU(有关更多详细信息,请参见《深度学习:神经网络世界中的沉浸》)。 但是,使ReLU比其他激活功能更具吸引力的主要功能是其简单的导数计算:
$$ display $$ d(ReLU(x))= \开始{cases} 1,x> 0 \\ 0,x <0 \ end {cases} $$ display $$
因此,ReLU在计算上比其他激活函数(S型,双曲正切等)更有效。
全连接层
现在该讨论完全连接的层了。 在所有其他权重中,最重要的是,因为所有权重都位于该层中,必须对其进行调整才能使神经网络正常工作。 完全连接的层只是权重矩阵:
$$显示$$ W = | w_ {i,j} | $$显示$$
当权重矩阵乘以输入列时,将获得一个新的内部表示形式:
$$ display $$ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $$ display $$
哪里
$ inline $ \ boldsymbol {x} $ inline $ 有大小
$内嵌$输入\ _shape $内嵌$ 和
$ inline $ x_ {new} $ inline $ --
$ inline $输出\ _shape $ inline $ 。 举个例子
$ inline $ \ boldsymbol {x} $ inline $ -784维向量,以及
$ inline $ \ boldsymbol {x} _ {new} $ inline $ 是100维向量,则矩阵W的大小为100x784。 事实证明,在这一层上的权重为100x784 = 78,400。
随着误差的反向传播,需要对该矩阵的每个权重取导数。 简化问题,只取关于
$内联$ w_ {1,1} $内联$ 。 当矩阵和向量相乘时,新向量的第一个元素
$ inline $ \ boldsymbol {x} _ {new} $ inline $ 等于
$ inline $ x_ {new〜1} = w_ {1,1} \ cdot x_1 + ... + w_ {1,784} \ cdot x_ {784} $ inline $ 和
$ inline $ x_ {new〜1} $ inline $ 由
$内联$ w_ {1,1} $内联$ 会很简单
$内联$ x_1 $内联$ ,您只需要取上述金额的导数。 所有其他权重也类似。 但这不是错误反向传播算法,只要它只是导数矩阵即可。 您需要记住,从下一层到这一层(误差从头到尾都出现)是一个100维梯度向量
$内联$ d \粗体符号{z} $内联$ 。 此向量的第一个元素
$内联$ dz_1 $内联$ 将乘以“参与”创造中的导数矩阵的所有元素
$ inline $ x_ {new〜1} $ inline $ ,即
$ inline $ x_1,x_2,...,x_ {784} $ inline $ 。 同样,其余元素。 如果将其翻译为线性代数的语言,则其编写方式如下:
$$ display $$ \ frac {\部分L} {\部分W} =(d \粗体符号{z},〜dW)= \左(\开始{矩阵} dz_ {1} \ cdot \粗体符号{x} \ \ ... \\ dz_ {100} \ cdot \ boldsymbol {x} \ end {matrix} \ right)_ {100} $$ display $$
输出为100x784矩阵。
现在,您需要了解要转移到上一层的内容。 为此,并且为了更好地理解现在发生的情况,我想写下用略有不同的语言在该层上使用导数时发生的情况,以避开“再乘以”到函数的细节(再次)。
当我想调整权重时,我想对这些权重取误差函数的导数:
$ inline $ \ frac {\部分L} {\部分W} $ inline $ 。 上面显示了如何取误差函数和激活函数的导数。 因此,我们可以考虑这种情况(在
$内联$ d \粗体符号{z} $内联$ 错误函数和激活函数的所有派生函数均已存在):
$$ display $$ \ frac {\部分L} {\部分W} = d \粗体符号{z} \ cdot \ frac {\部分\粗体符号{x} _ {新}(W)} {\部分W} $ $显示$$
可以这样做,因为您可以考虑
$ inline $ \ boldsymbol {x} _ {new} $ inline $ 作为W的函数:
$ inline $ \ boldsymbol {x} _ {new} = W \ cdot \ boldsymbol {x} $ inline $ 。
您可以将其替换为上面的公式:
$$ display $$ \ frac {\部分L} {\部分W} = d \粗体符号{z} \ cdot \ frac {\部分W \ cdot \粗体符号{x}} {\局部W} = d \粗体符号{ z} \ cdot E \ cdot \ boldsymbol {x} $$显示$$
其中E是由单位组成的矩阵(不是单位矩阵)。
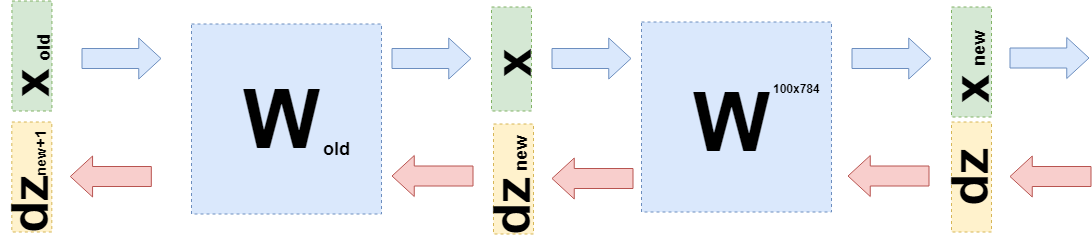
现在,当您需要采用上一层的导数时(即使为了简化计算,它也将是一个完全连接的层,但是在一般情况下它不会改变任何内容),那么您需要考虑
$ inline $ \ boldsymbol {x} $ inline $ 作为上一层的函数
$ inline $ \ boldsymbol {x}(W_ {old})$ inline $ :
$$ display $$ \开始{聚集} \ frac {\部分L} {\部分W_ {old}} = d \粗体符号{z} \ cdot \ frac {\局部\粗体{x} _ {new}(W )} {\部分W_ {old}} = d \粗体符号{z} \ cdot \ frac {\局部W \ cdot \粗体符号{x}(W_ {old})} {\局部W_ {old}} = \\ = d \ boldsymbol {z} \ cdot \ frac {\部分W \ cdot W_ {old} \ cdot \ boldsymbol {x} _ {old}} {\部分W_ {old}} = d \ boldsymbol {z} \ cdot W \ cdot E \ cdot \ boldsymbol {x} _ {old} = \\ = d \ boldsymbol {z} _ {new} \ cdot E \ cdot \ boldsymbol {x} _ {old} \ end {gathered} $$显示$$
恰好
$ inline $ d \ boldsymbol {z} _ {new} = d \ boldsymbol {z} \ cdot W $ inline $ 并且您需要发送到上一层。
代号
本文的主要目的是解释神经网络的数学。 我将很少的时间花在代码上。
这是错误函数的示例实现:
class CrossEntropy: def forward(self, y_true, y_hat): self.y_hat = y_hat self.y_true = y_true self.loss = -np.sum(self.y_true * np.log(y_hat)) return self.loss def backward(self): dz = -self.y_true / self.y_hat return dz
该类具有直接和反向传递的方法。 在直接传递时,类实例将数据存储在图层内部,而在返回传递时,它将使用它们来计算梯度。 其余各层以相同的方式构造。 因此,可以编写这种风格的完全连接的神经元:
class MnistNet: def __init__(self): self.d1_layer = Dense(784, 100) self.a1_layer = ReLu() self.drop1_layer = Dropout(0.5) self.d2_layer = Dense(100, 50) self.a2_layer = ReLu() self.drop2_layer = Dropout(0.25) self.d3_layer = Dense(50, 10) self.a3_layer = Softmax() def forward(self, x, train=True): ... def backward(self, dz, learning_rate=0.01, mini_batch=True, update=False, len_mini_batch=None): ...
完整的代码可以在
这里找到。
我也建议
在Habré上研究这篇
文章 。
结论
我希望我能够解释并证明神经网络背后是相当简单的数学,这一点也不可怕。 但是,为了更深入地了解,值得尝试编写自己的“自行车”。 更正和建议很高兴在评论中阅读。