👐🏼 🕖 ✍🏻 物理与经济学。性别学差异及其在IT中的体现 🤰🏽 😿 🅱️

我从理论物理学来到IT领域。他主要从事经济工作。从事-这：分析，传统知识，陈述，设计，编程。自然，我一直都比较物理和经济方法来分别理解自然规律和经济学规律。在这个问题上已经有了某种观点。关于她，将进行讨论。

1.关于一般的认知

有两种识别方法：

亚里士多德的方法 。这是一种整体方法，将对象视为黑匣子。现象，客体是作为一个整体进行研究的。例如，现实表明，重物掉落到地面的速度比轻物要快。剩下的一个移动的身体逐渐停止。亚里士多德的方法将这种现象视为一个整体现实，因此可以将其称为现象学。

伽利略的方法 。这是一种分析性的系统方法。这就是分而治之的方法。现象，对象分解成其组成部分，并分别从其余部分中进行抽象研究（分析）。然后，考虑到组件之间的相互作用（合成），可以将生成的图片合并为一张。例如，物体的跌落被视为物体在空隙中的跌落。然后它们以相同的加速度下降。但实际上，与空气的摩擦会阻止它们均匀下落。单独研究了这种力量，我们可以解释亚里斯多德的结果。同样，如果我们脱离摩擦力，则移动体将移动而不会停止。如果考虑到摩擦力，我们将得到亚里士多德的结果。伽利略的方法立即导致需要研究力量。最后，这转化为经典物理学的连贯系统。

再次，为了清楚起见。

亚里士多德的方法 。有一个现象正在研究中，“人体从空中坠落到地面上”是F.现象，我们对不同的物体进行了研究，发现较重的物体比轻的物体掉落到地面的速度更快。

伽利略的方法 。在研究F现象时，不仅要考虑体重。我们研究空中坠落。让我们不仅改变重量，还改变空气。让我们尝试降低其密度，以便最终没有空气。然后我们发现所有物体都以相同的加速度掉入空隙。我们找到影响现象的参数，并尝试创建仅一个参数有意义的条件。这不是自然。因此，物理学家需要一个可以改变参数的实验室。在研究了一个参数的影响之后，我们可以继续研究另一个参数的影响。我们正在尝试将整个方法的复杂性降低为简单方法的组成。通过改变下落物体的形状，我们可以研究摩擦力对空气的依赖性，具体取决于物体的形状。通过改变下降速度，我们可以检测到摩擦力对速度的依赖性。通过改变跌倒的高度，我们可以检测加速度对高度的依赖性。通过改变地球上的地理位置，我们发现坠落加速度对地理的依赖性。

粗略地说，他们以亚里士多德的方法研究现实，以伽利略的方法研究抽象，并通过综合将它们抽象为现实。

2.物理知识模型

物理学是包括经济学在内的许多科学的理想理论。在物理实验中，获得了一系列离散值。但是它们被认为是连续函数的近似值，而连续函数实际上是物理指标。物理学家正在尝试猜测这些功能。因此，伽利略（Galileo）猜测抛物线是与地平线成一定角度投掷石头的轨迹。开普勒猜测了行星的轨迹-椭圆等。猜测了轨迹之后，我们得到了一种预测装置-能够计算轨迹的未探索坐标的值。为了进行测试，他们进行了一项实验-为获得所需价值的实验创造条件。然后，在验证了预测值和实验值之后，我们得到了理论的证实或反驳。在这里，有时实验误差的误差起着重要的作用。物理知识归结为确定性的确定-从初始状态获得状态的定律：

（ ） （ ， （ ） ）

$S（t）= D（Q，S（0））$

S(0) -   D –  – ,  S(t)  S(0) Q –       . ,  ,      .

因此，对于从（0,0）点以一定速度抛出的石头 $v_0$ 倾斜 $α$ 到地平线

$$显示$$ x（t）= v_0 tcos⁡（α），y（t）= v_0 tsin⁡（α）-（gt ^ 2）/ 2 $$显示$$

初始状态 S（0）由三个参数设置：出发点（0,0），初始速度 $v_0$ 角度 $α$ 。
环境Q的影响由重力加速度g给出。当扩大问题的范围（高初始速度）时，g不再恒定。
确定性D由上式给出。

对于更现实的任务，必须考虑与空气的摩擦。这使问题的数学运算复杂化，但是原理保持不变。您可以考虑用飞机代替石头。然后飞机的推力开始发挥作用，并由飞行员进行调节。一个非物理因素也会出现-飞行员的意愿。我们不能考虑到它。但是我们知道，它不是无限的：牵引力不能无限，加速度不能无限。这在运动中引入了确定性元素。他们使用它来建立防空导弹的弹道。

让我们回到飞石上。它的特点是无限数量的物理参数。例如，仅其形状可以是任意复杂的。但是我们确信，在某些有用的领域中，我们可以将石材视为重要材料。这是古典力学的主要抽象。所有系统都表示为相互作用的材料点集。这使得主要的认知减少-将复杂系统的行为减少到其基本组件的行为。

与提到的认知还原有关，可以区分两种认识论方法：还原论和整体论。

3.还原主义和整体主义

还原论是从子系统的特征和子系统的相互作用的特征中减少系统特征的原理。成功从事物理学。
考虑例如气体。无需将其分解为子系统，我们可以使用实验现象学概念进行操作：压力P，温度T，体积V。根据经验，我们找到连接这些参数的关系-气体状态方程：

常 量

$PV =常量$

这就是所谓的现象学层面-处理现象（现象）而不进入其结构。这是亚里斯多德的方法。

现在应用伽利略的方法。我们分解“气体”系统：将其想象为碰撞分子的集合。然后我们通过分子的机械参数定义P和T。这是在分子物理学中完成的。因此，我们将气体系统简化为分子子系统。这将阐明状态方程或推导新系统的状态方程。

因此，在商业中，我们有一个类比：宏观经济学被分解为企业和家庭。但是在此减少尚不完美。 las，没有经济牛顿。问题是物理上没有的主观因素的复杂性和可用性（尽管存在有关该主题在量子力学中作用的争论）。

现在关于整体主义。

整体性是系统中可能存在不可约性质的原理。因此，在生物学中，生命主义的学说是基于Entelechy概念的，Entelechy是体内整体固有的，不可还原的生命力。

迄今为止，物理学没有涉及整体论的概念。

4.公式和算法模型

公式模型是由公式定义的模型。 “公式”的概念将被认为是已知的。

物理学中的例子：牛顿方程，拉格朗日方程，麦克斯韦方程，Navier-Stokes方程，Heisenberg-Schrödinger方程，爱因斯坦方程。

经济方面的示例：期权价格的Black-Scholes公式，货币供应量公式，用于优化金融投资组合的线性规划模型，利息计算公式，风险计算公式。

使用公式化模型，一个人无需计算机即可工作。这几乎是所有纯数学。但是在这里，算法扮演着越来越重要的角色。因此，没有将四种颜色问题的解决方案简化为任何公式，而是需要在许多特殊情况下采用蛮力解决方案。此半身是由计算机完成的。

算法模型 -由算法定义的模型，可能无法简化为公式。当然，可以将算法分类为公式，但是这些不是相同的经典公式。该算法模型最初仅使用计算机是现实的
形式模型总是可以简化为算法模型。

第一个算法模型的一个例子是Fermi-Pasta-Ulam问题。以下是乌兰的书《数学历险记》的引文。

报价单

_{机器制造完成后，费米凭着直觉和极大的常识立即意识到了它们在理论物理学，天体物理学和古典物理学问题研究中的所有重要性。} _{我们以最详细的方式讨论了此问题，并决定尝试提出一些问题，这些问题的解决方法很简单，但解决方案需要很长的计算时间，而这在笔和纸或现有的机械计算设备的帮助下是不可能的。} _{在讨论了许多可能的问题之后，我们解决了一个与动力系统的长期行为有关并且需要长期预测的典型问题。} _{它考虑了具有两个固定端的弹性绳，它不仅受到通常与变形成比例的弹性变形力的影响，而且还受到较小的物理非线性力的影响。} _{有必要找出在大量的振荡周期之后，这种非线性将如何逐渐影响一个键的已知振荡周期行为，其他键如何获取其振幅，以及我们如何推理运动会被热化，从而模仿行为最初是层流的液体变得越来越湍流，直到最终它们的宏观运动转化为热量。}

最近来到洛斯阿拉莫斯的物理学家约翰·帕斯塔（John Pasta）帮助我们在MANIAC上创建了流程图，编程和处理任务。费米决定学习如何对机器编程。在那些日子里，当现成的程序和已建立的规则已经存在并且此过程本身是自动化的时，要比现在做起来困难得多。然后有必要学习各种技巧。 Fermi非常迅速地掌握了它们，并教会了我一些知识，尽管我已经足够了解如何评估可以用这种方式解决的任务，确定计算步骤的持续时间并了解其实现原理。

事实证明，我们非常成功地选择了任务。从定性角度获得的结果与费米对波运动最深的知识所期望的结果完全不同。最初的目标是观察最初嵌入简单正弦波（音符为一个音调）中的弦能量以何种速度逐渐产生更高的谐波，以及系统如何达到最终的混沌状态，从而描述弦的形状，因此能量越来越高之间分配的本质。但是没有发生任何事情。令我们惊讶的是，琴弦仅在几条聋哑音符上开始演奏，而且，在经过数百次普通往复振动后，它再次呈现出与开始时几乎相同的正弦曲线形状，这可能更令人惊讶。

正如他本人所说，我知道费米认为这是“次要发现”。但是一年之后，当吉布斯（Gibbs）邀请他演讲时，他打算向他讲述他（这是美国数学学会年会上非常光荣的事件）。他在会议之前病倒了，这次演讲从未举行。但是，仍然发表了由费米，帕斯塔和我撰写的有关这项工作的报告，作为洛斯阿拉莫斯工作的报告。

我必须解释一下，如果我们想象一个字符串由有限数量的粒子组成-在我们的例子中是64或128个粒子，那么可以使用计算机来研究诸如字符串之类的连续介质的运动。（元素的数量最好用2的幂表示，因为这有助于在计算机上进行处理。）这些粒子由力链接在一起，这些力除了距离线性项外还包含小的非线性二次项。然后，机器可以快速计算出这些点在短时间内的运动。计算了一个职位后，她进入了另一个时间阶段并计算了一个新职位，因此重复了很多次。绝对没有办法手动进行此计算，这实际上需要数千年。在此，使用19世纪和20世纪经典分析的数学方法以解析形式进行求解是完全不能接受的。

结果确实令人震惊。已经进行了许多尝试来阐明这种周期性和规律性行为的原因，这已经成为当今关于非线性振荡的大量文献的来源。普林斯顿大学的物理学家马丁·克鲁斯卡尔（Martin Kruskal）和在贝尔电话实验室（Bell Telephone Laboratory）工作的数学家诺曼·扎布斯基（Norman Zabuski）对此进行了研究。后来，彼得·莱克对这一理论做出了杰出的贡献。他们都对这种问题进行了有趣的分析。数学家知道，所谓的返回庞加莱动力学系统（包括许多粒子）具有巨大的长度（实际上是在天文尺度上），并且迅速返回其原始位置是最令人惊讶的。

另一位洛斯阿拉莫斯（Los Alamos）的物理学家詹姆斯·苏（James So）决定查看从非常接近的初始位置返回初始位置后的周期是否再次从同一状态开始，以及在第二个“周期”之后会发生什么。他与Pasta和Metropolis一起重复了整个过程，令人惊讶的是，再次出现了这种情况，但是准确率不到百分之一。进一步重复了这张图片，但是在六个或十二个这样的周期之后，精度又开始提高，这表明出现了某个“超级周期”。因此，一个陌生人紧随其后。

以下是有关哈布雷的文章，介绍了费米·帕斯塔·乌拉姆问题的现状：
数学家解决了费米-帕斯塔-乌拉姆问题

5.协调

通过系统协调，我的意思是定义基本参数，这些参数原则上决定系统的发展。例如，在实体点的力学中，坐标定义为：

外力F
- 质量m物质点
- 物质点的空间坐标（x，y，z）= r
- 时间t

系统的演化由牛顿方程给出

（ （ ） ） （ ） （ ） ）

$（d ^ 2 r（t））/（dt ^ 2）= [F（t））/ m$

经济实体的协调是什么？我曾经在商业智能系统上工作。它的主要术语是指标。该系统的基础是记分卡。数百个指标。但是，我在互联网上徒劳地搜索了指标基础的描述-一组指标不能归结为其他指标，并且从原则上讲，它们完全确定了经济实体的发展。也就是说，据我所知，经济方面尚未进行协调。因此，尚不可能讨论一些基本的动态定律。仅基于指标的连接，才有可能进行方案分析-回答以下问题：“如果基础指标根据给定方案发生变化，则派生指标将发生什么？”

6.抽象的例子。像物理一样进行时间序列预测

您可以根据实际时间序列提出预测问题：拥有多个实际值，您需要获取指标的预测值-将来的值。这暗示了时间序列的一种隐藏的确定性。关于这个问题有许多科学和伪科学的推测。我本人与理学博士打交道，他们声称他们的方法可以使他们获得汇率预测，并显示具有各种置信区间和分布规律其他属性的相应论文。但是，当面对现实时，这些技术就被吹走了。

有时要获得预测，请执行以下操作：

取实时序列{V（ti）}。日程安排-步骤虚线。
取一个连续函数W（t），使W（ti）= V（ti）。该图是连续曲线。
选择多项式P（t），以足够的精度近似W（t）。可以考虑所有t的多项式。
然后我们对未来时间T有一个预测：V（T）= P（T）
所有这些都给人以科学的印象，但只是乍一看。是的，W（t）的近似多项式的存在是由Matanalysis的Weierstrass定理保证的。我们可以任意精确地对W（t）进行多项式化。但是它不能用于预测。

实数序列的近似值为100％，预测值为零。多项式可以任意发明，但是它们都会给出不同的预测。

当第T天到达时，我们找到了真实的V（T），那么对于序列{{V（ti）}，V（T）}，我们可以构造一个新的多项式Q（t），它精确地近似于该序列，但是时间T不再是未来和Q（T）不再是预测，而是现实。多项式P（t）和Q（t）绝对不必重合，并且对于新的预测时间T'> T，它们将显示不同的结果。也就是说，没有预测。似乎有科学，但没有预测。就像中世纪的天使理论一样。她可以解释一切，但无法预测任何事情。

物理内插与经济外推之间的区别：

经验数据的准确性 ：物理近似，经济学精确
领域功能 ：物理学上连续，不连续，经济学上逐步
经验数据 ：在物理上是离散的，在经济学上是连续的，具有离散的间断
基本定律 ：在物理学那里。例如，F = ma；在经济中呢

7.经济学与物理学

在经济学中，实际轨迹（基本上是不连续的）是分段恒定函数。例如，“汇率”指示器可以随时跳转。连续的经济功能-为了进行分析而近似（如果您手中有铁锤，那么您想考虑任何物体，例如钉子...）。每次会计交易都会导致帐户衍生工具指标值跳升。它们是大多数指标。此外，工人人数的每次变化都是离散的，等等。经济轨迹的连续性与大多数物理轨迹的连续性形成对比。因此，matanalysis的设备不能直接应用于经济轨迹。

图片为物理认知。与水平线成一定角度扔石头的轨迹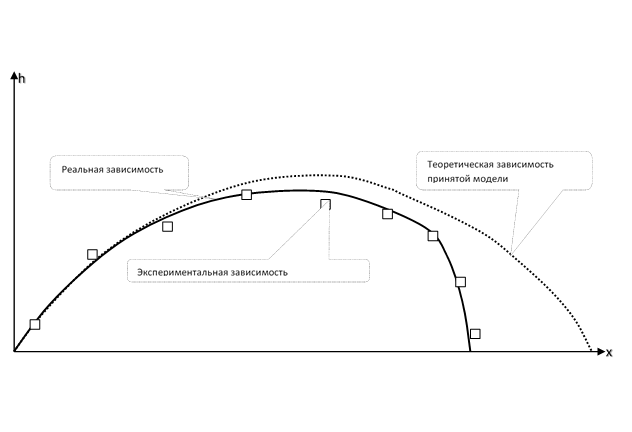

了解经济知识。中央银行的货币汇率。

这是真正的实验精确功能。它在汇率变化的时间点是不连续的。

在物理学中：

实验物理值几乎总是近似值
实验物理值形成离散序列。
实验离散序列被视为连续逼近的多边形，因为现实是连续的。连续性的概念可能只是在较小的时空尺度上说谎。然后物理学将改变它的面貌。
明确定义的基准指标
理论轨迹和实际轨迹几乎总是连续的，并且几乎总是可微的（实体点的轨迹在时间上总是可微二倍的）
由于真实动力学和真实轨迹的连续性，其良好的连续逼近具有预测能力：在足够小的邻域中，函数不会偏离其最后的真实值。

在经济中：

实验经济价值可以被认为是准确的。由于大量的商业实体，只有在宏观经济学中才存在准确性问题。
实验经济价值包括稳定区间，当价值突然变化时，该区间会在某些时间点中断
实验数据不能视为连续逼近的试验场，因为现实是不连续的。
没有完全定义的基线指标。不清楚为什么跳舞。
由于真实轨迹的不连续性，任何任意良好的连续逼近都不能保证在任意较小邻域中进行预测。
实际轨迹几乎总是不连续的。这意味着经济确定需要不同于古典力学的方法。
在经济中，最初有一个经济实体的自由意志因素。其范围由国家规定。这种自由的极限：
-在非国家监管的市场中享有完全自由
-在部分受国家管制的市场中的部分自由
-在没有自由市场的完全集中化的状态下完全缺乏自由

经济知识尚未达到类似于经典力学的水平：

物料点类型的基本成分未定义
没有定义Q（环境参数），不清楚什么重要，什么不重要，
尚未对经济体系进行详细的分层，
; .

. – . – . ? , . . . . , – .

, . , , - .

8. IT

8.1.

. . . . , . . . . . . . , , . . … , . . , . . . , . . . . . . . . . . . – " . - "!? , . -1840( , ). . . , . , . , . , . . , , . (). . , , , : ", . ". ! . , , - .

8.2. -

. — . , , .. . . , . . – . , . , . – . . …

. . , . , , , . , . . . . . , - . . . . , : , . . . , , . . ? . . , .

. - , .

, , . , . . , .

. . . , . , . , : , . , . . .

, – Jump Processing. , . .

, . “ ”. , – . , , . – , . . , – .

8.3.

( ). . “”. . , . , . . – . . , . . . . , . . – . . , . … . ? , . , - . . . , . , , . . .

. , . , . , – . , . , – ( – ?).

8.4.

_{“ ”}

. () . . . , , . . , . . , , . . . – . , , . , . . , . 真好 . – . , . – . . , (, ). , . . , . . , , , . . . – . . . . . . . . . : , , , , , , , , … . 100 . ( , , ) . , ( , (SQL-) ). , . 即 . . . , . . , : ”, . . . ”.

. , . , . : . , , .

. . . , , . . . . -.

() . , , ( ), . , . , – . , , , , , . . . , , . , “” “”. , “” “”. ? , .

: . . . , . . . . — . . : . : , …

. . , . . .

, . . - . . — . 怎么会这样 .

: IT. .

物理与经济学。 性别学差异及其在IT中的体现