我们根据图针对更广泛的行为类别进行逻辑函数的计算。 我们考虑不包含多个信号(或以其他方式:不包含索引事件)的循环自主行为。 另一个限制:为方便起见,我们将不考虑OR中并行分支的连接。 我们仅考虑通过AND进行的连接,即,仅当触发了所有其先前事件时才触发事件。
我们将使用STG描述行为,但有其他限制。 对于每个地方,进入和离开它的弧数严格等于一个。 因此,可以将具有传入和传出弧的地方视为连接两个事件(过渡)的一个弧。 因此,标记沿着弧线移动。 由于现在不考虑具有多个信号的行为,因此禁止了事件索引,因此不需要它们。 禁止空事件。 当一个事件中包含的两个弧线从彼此不平行的事件中出现时(同样情况是特殊情况),也禁止这种情况。 这样做的目的是消除不承载语义负载的弧。 考虑到上述限制,从STG行为的角度来看,其余部分被认为是正确的(正常,活动,安全)。 该行为不包含CSC冲突。
定义1.电弧进入的事件是该电弧退出的事件的结果。 相反,电弧退出的事件是该电弧进入的事件的原因。
定义2.路径-无尽的事件序列-图形标记更改的结果,从特定的路径开始。 每个事件都会无数次进入序列。 每个此类条目都是唯一的。
定义3.事件A的踪迹是所有事件要么是事件A的直接后果,要么是事件的后果与事件A的关系的传递性闭合的结果的路径。事件A的踪迹的初始标记如下建立。 如果标记被任意更改,则在触发事件A之后,事件A的输出弧中的标记将被固定。 然后,其余标记移动,直到没有释放事件A的输出弧中的标记就不可能移动标记为止。所得标记是事件A轨迹的初始标记。
定义4.我们介绍三个事件(A,B,C)的排序关系。 当且仅当对于事件A的任何踪迹,序列中事件B的第一次出现总是比事件C的第一次出现更早发生时,才对三个事件进行排序(写为A> B> C)。
备注。 事件A可以与事件B和C都平行(或仅与C平行),或者事件A和B都可以与事件C平行。
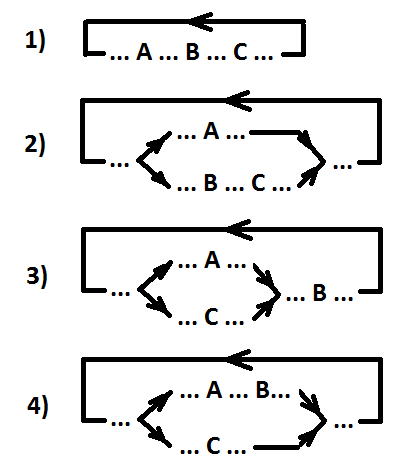
有序事件A,B和C的位置选项(A> B> C)。
定义5.如果满足以下条件,则信号b(开关B1和B2)针对事件X和Y(事件X和Y平行或一致)拾取信号a(开关A1和A2):
1)X> A1> A2;
2)如果事件A2与事件X平行而不与事件Y平行,则X> A2> Y;
3)Y> B1> B2;
4)如果事件B2与事件Y平行而不与事件X平行,则Y> B2> X;
5)Y> B1> A2;
6)如果事件A2与事件Y平行而不与事件X平行,则Y> A2>X。
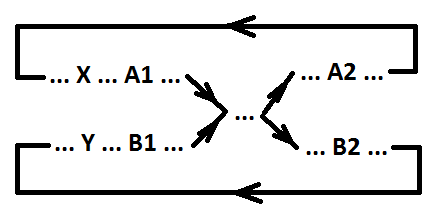
备注1.条件1、2和3、4分别确定信号a和b的切换顺序。 条件5、6指定捕获事件B1和捕获事件A2的顺序。
备注2.事件X可以是事件A1。 在这种情况下,条件1和2退化。
备注3.事件Y可以是事件B1。 在这种情况下,条件3、4和5退化。
备注4.事件X可以是事件A1,事件B1也可以是事件Y。 在这种情况下,条件1、2、3、4和5退化。
现在我们开始考虑什么是植入物。 牵连者的特征是事件,其结果是牵连者改变了其含义。
定义6.一个事件,其结果是隐含的AND(OR)将其值从1(0)更改为0(1),我们将其称为隐含的右边界。 与此事件对应的信号将被称为打开。 牵连的人打开了。
定义7.一个事件,其结果是隐含的AND(OR)将其值从0(1)更改为1(0),我们将其称为隐含的左边界。 与此事件对应的信号将被取消。 紧急关闭。
定义8.任意两个右(或任意两个左)边界彼此不平行的隐含符将称为不连续。
目前,我们不会考虑打断植入物。 我们将在下面返回他们的考虑。
因此,我们得到:牵连者的所有右边界彼此成对平行,而牵连者的左边界彼此成对平行。
重要属性。 当发生至少一个事件时,该事件将打开,这是事件的右边界。 仅当作为隐含对象的左边界的所有事件都发生时,隐含对象才会关闭。
现在剩下的工作就是确定形成植入物的信号的特性。
定义9.植入物中包含的信号将称为变量。
变量的第一个属性。 开启和关闭信号是可变的。
变量的第二个属性。 对于任何切换变量(其切换之一是牵连项L的左边界,另一个是某个事件X),必须存在一个事件-同一牵连项的某个右边界R使得X和R是同一事件,或者R > X>L。
变量的第三个属性。 对于任何包含变量(其开关之一是牵连者R的右边界,另一个是某个事件X),必须存在一个事件-同一牵连者的某个左边界L使得X和L都是同一事件,或者R > X>L。
变量的第四个属性。 对于任何未打开或关闭的变量(开关X1和X2),必须发生两个事件:牵连对象L的某个左边界和牵连对象R的一些右边界,使得R> X1> L和R> X2> L 。 否则,暗示者无法在关闭位置保持恒定值。
变量的第五个属性。 对于任何一对:某个开关变量和某个开关变量,必须有一系列变量针对隐含的右边界相互拾取(对于不同的拾取器,右边界可能会变化),从此开关变量开始并以该开关变量结束。 否则,暗示者将无法在开启位置保持恒定值。
变量的第六个属性。 对于任何包含变量a,如果蕴含项的右边界是事件a +(a-),则将此类变量包含在含蕴含项的AND(OR)的记录中,并包含在反相中,以及包含包含在内的含蕴含项(+)的事件。 对于任何切换变量a,如果蕴含项的左边界是事件a-(a +),则将这样的变量a包含在含蕴含项的AND(OR)的记录中,并且包含在反相的隐含蕴含项(-)中。
变量的第七个属性。 由于变量的第四属性,对于每个未打开或关闭的变量a,蕴含量R的右边界和蕴含量L的左边界,使得R> a +> L且R> a->L。 如果R> a +> a-,则这样的变量将带倒数输入And的含义,而将不带倒数的OR的含义输入。 如果R> a-> a +,则这样的变量将不经求反而输入隐含AND,而对具有求反的隐含OR进行输入。
列出的七个变量属性是蕴含项的必要属性。 而且,这些性质足以描述植入物。
备注。 当植入物的某些左边界可以平行于同一牵涉者的某些右边界时,对植入物的上述描述不禁止这种情况。 这种现象的含义是,根据并行处理的速度,对于实施相应的信号可能不需要实时进行这种植入,并且可能无法实时关闭(如果右边界的工作早于左边界的话)。
现在,我们将考虑如何从蕴含函数构建逻辑函数的普通形式。
定义10.如果对于某些状态,牵涉者处于关闭位置(植入物AND(或)的值为1(0)),我们说牵涉者涵盖了该状态。
考虑某个信号x,我们需要为其计算逻辑函数。 为了构造DNF(CNF),必须使AND(OR)隐含性覆盖函数x为1(0)的所有状态。 在这种情况下,有必要使所有这些AND(OR)含义都不覆盖其中函数x为0(1)的状态。 同样,在计算逻辑功能时,有必要考虑电路的具体情况:牵涉对象应“重叠”。 也就是说,如果在某种状态下该隐含对象可以打开(即,可以触发一个事件,该事件是该隐含对象的右边界),并且信号功能x的值在此切换期间没有变化,则必须有另一个隐含对象覆盖此状态,并且触发此事件时不会打开。
现在我们需要澄清三个问题。 就图而言,状态是什么? 如何确定信号函数x为1(0)的状态? 如何确定植入物覆盖的条件?
让我们从状态开始。 任何可达到的标签都是一个条件。 由于没有CSC冲突,因此每个可实现的标签都对应一个唯一状态(可实现)。 在无法达到的状态下,函数的值是任意的,因此无需考虑它们。 因此,我们考虑的每个状态都由相应的标签唯一地描述。 每个标记的位置由其标记的弧唯一确定。 每个弧都与一对(有序的)事件唯一关联:弧从其退出的事件和弧进入的事件。 因此,任何可达到的状态都是由一组有序事件对组成的集合来唯一描述的。
定义11.一对表示标记弧的事件将被写入{P,S},其中P是原因事件,而S是后果事件。
定义12. MM将被称为有序对{P,S}的集合,它描述了某些可达到的状态。
现在,让我们确定函数x的值是1的状态,并且它是0的状态。让事件x +由n个事件A1,A2,...,An引起,而事件x-由m个事件B1,B2,..., Bm。
在以下情况下,函数x的值为1:
或1)对于从1到n的每个i,对{Ai,x +}属于集合MM;或者
2)一对{x +,S},使得x +> S> x-属于集合MM;或
3)一对{P,S},使得x +> P> x-和x +> S> x-属于集合MM;或
或4)一对{P,x-},使得x +> P> x-属于集合MM,并且存在从1到m的i,使得对{Bi,x-}对不属于集合MM。
在以下情况下,函数x的值为0:
或1)从1到m的每个i,对{Bi,x-}属于集合MM;或者
2)一对{x-,S},使得x-> S> x +属于集合MM;或
3)一对{P,S},使得x-> P> x +和x-> S> x +属于集合MM;或
或4)一对{P,x +},使得x-> P> x +属于集合MM,并且存在从1到n的i,从而使得对{Ai,x +}不属于集合MM。
现在我们找出植入物覆盖的条件。 令蕴含者具有n个左边界L1,L2,...,Ln和m个右边界R1,R2,...,Rm。
如果属于集合MM的对{P,S}中的至少一对满足以下条件,则暗示者不覆盖集合MM所描述的状态:存在i从1到n,j从1到m,使得
1)Li和S是同一事件,并且Rj> P> Li,
或2)Rj和P是同一事件,并且Rj> S> Li,
或3)Rj> P> Li和Rj> S> Li。
凭借变量的第五个属性,此语句是正确的。
如果对于属于集合MM的{P,S}对都不满足以下条件,则隐含式覆盖集合MM所描述的状态:存在从1到n的i和从1到m的j
1)Li和S是同一事件,并且Rj> P> Li,
或2)Rj和P是同一事件,并且Rj> S> Li,
或3)Rj> P> Li和Rj> S> Li。
由于变量的第二,第三和第四属性,此语句是正确的。
形象地讲,如果所有标记都在隐含符号的左右边界之间,则隐含符号覆盖了状态。 如果至少一个标记位于这些边界之外,则植入物不会覆盖该状态。
现在,我们有了用于计算法线形式的工具(目前尚不清楚,但是对于间歇性植入物仍然存在问题)。 但是我们对最小范式感兴趣(考虑到电路的具体细节)。 在继续进行之前,让我们回到间歇性含义的考虑上。 考虑DNF信号x的I隐含(CNF的OR隐含的情况相似)。 假设相同的蕴含符L1和L2的两个左边界彼此不平行,并且L1> L2> x-(两个右边界的情况类似地考虑)。 然后,蕴含符R1和R2必须有两个右边界,这样对于L1和R2以及L2和R1对,必须满足变量的第二,第三,第四和第五个属性。 如果存在一个平行于L1的左边界L3,那么对于L3和R2对,还必须满足上述特性(类似地,在存在相应边界的情况下,平行于边界L2,R1和R2的含蓄量)。 但是,由于没有使用多个信号,因此必须存在一个具有边界L1和R2(以及平行的对应边界,如果有任何中断的暗示者具有边界)的不连续的暗示者。 在这种情况下,非不连续蕴含量由较少的变量组成,并且覆盖了不连续蕴含量所覆盖的所有状态,信号函数x的值在这些状态上为1。
下一部分将详细介绍如何计算最小函数。