
我们将继续发布对最近的冠军赛提出的任务的分析。 接下来的是机器学习专家的资格回合中的任务。 这是四个(后端,前端,ML,分析)的第三条轨道。 参与者需要建立一个纠正文本输入错误的模型,提出一种在老虎机上玩的策略,想到一个针对内容的推荐系统,并编写更多程序。
A.错别字
条件
(史诗)(来自一个论坛)
-谁胡说八道?
-天体物理学家。 他们也是人。
-您在“新闻记者”一词中犯了10个错误。
许多用户会输入错误,有些是因为按下键,有些是因为他们的文盲。 我们要检查的是,用户实际上是否还记得他键入的其他单词。
更正式地,假设发生以下错误模型:用户从他要写的单词开始,然后在其中产生许多错误。 每个错误都是将单词的某个子字符串替换为另一个子字符串。 一个错误对应于仅在一个位置进行替换(即,如果用户希望通过规则“ abc”→“ cba”进行单个错误,则可以从字符串“ abcabc”中获取“ cbaabc”或“ abccba”)。 每个错误之后,该过程都会重复。 相同的规则可以在不同的步骤中多次使用(例如,在上面的示例中,可以通过两个步骤获得“ cbacba”)。
如果用户记住一个给定的单词并写出另一个给定的单词,则需要确定用户可能犯的最小错误数。
I / O格式和示例输入格式
第一行包含该单词,根据我们的假设,该单词是用户想到的(它由小写拉丁字母组成,长度不超过20)。
第二行包含他实际写的单词(也由小写拉丁字母组成,长度不超过20)。
第三行包含单个数字N(N <50)-描述各种错误的替换次数。
接下来的N行包含以下格式的可能替换项:<正确的字母序列> <空格> <错误的字母序列>。 序列不得超过6个字符。
输出格式
需要打印一个数字-用户可能犯的最小错误数。 如果该数字超过4,或者不可能从一个单词中得到另一个,请打印-1。
例子
解决方案
让我们尝试从正确的拼写中生成所有可能的单词,且错误不超过4个。 在最坏的情况下,可能会有O((L﹒N)
4 )。 在问题的局限中,这是一个相当大的数目,因此您需要弄清楚如何降低复杂性。 相反,您可以使用中间相遇算法:生成不超过2个错误的单词,以及可以从中获取不超过2个错误的用户编写单词的单词。 请注意,每个集合的大小不会超过10
6 。 如果用户犯的错误数量不超过4,则这些集合将相交。 同样,我们可以验证错误数量不超过3、2和1。
struct FromTo { std::string from; std::string to; }; std::pair<size_t, std::string> applyRule(const std::string& word, const FromTo &fromTo, int pos) { while(true) { int from = word.find(fromTo.from, pos); if (from == std::string::npos) { return {std::string::npos, {}}; } int to = from + fromTo.from.size(); auto cpy = word; for (int i = from; i < to; i++) { cpy[i] = fromTo.to[i - from]; } return {from, std::move(cpy)}; } } void inverseRules(std::vector<FromTo> &rules) { for (auto& rule: rules) { std::swap(rule.from, rule.to); } } int solve(std::string& wordOrig, std::string& wordMissprinted, std::vector<FromTo>& replaces) { std::unordered_map<std::string, int> mapping; std::unordered_map<int, std::string> mappingInverse; mapping.emplace(wordOrig, 0); mappingInverse.emplace(0, wordOrig); mapping.emplace(wordMissprinted, 1); mappingInverse.emplace(1, wordMissprinted); std::unordered_map<int, std::unordered_set<int>> edges; auto buildGraph = [&edges, &mapping, &mappingInverse](int startId, const std::vector<FromTo>& replaces, bool dir) { std::unordered_set<int> mappingLayer0; mappingLayer0 = {startId}; for (int i = 0; i < 2; i++) { std::unordered_set<int> mappingLayer1; for (const auto& v: mappingLayer0) { auto& word = mappingInverse.at(v); for (auto& fromTo: replaces) { size_t from = 0; while (true) { auto [tmp, wordCpy] = applyRule(word, fromTo, from); if (tmp == std::string::npos) { break; } from = tmp + 1; { int w = mapping.size(); mapping.emplace(wordCpy, w); w = mapping.at(wordCpy); mappingInverse.emplace(w, std::move(wordCpy)); if (dir) { edges[v].emplace(w); } else { edges[w].emplace(v); } mappingLayer1.emplace(w); } } } } mappingLayer0 = std::move(mappingLayer1); } }; buildGraph(0, replaces, true); inverseRules(replaces); buildGraph(1, replaces, false); { std::queue<std::pair<int, int>> q; q.emplace(0, 0); std::vector<bool> mask(mapping.size(), false); int level{0}; while (q.size()) { auto [w, level] = q.front(); q.pop(); if (mask[w]) { continue; } mask[w] = true; if (mappingInverse.at(w) == wordMissprinted) { return level; } for (auto& v: edges[w]) { q.emplace(v, level + 1); } } } return -1; }
B.多臂匪
条件
这是一个交互式任务。
您自己不知道它是怎么发生的,但是您发现自己在一个装有老虎机和整袋令牌的大厅里。 不幸的是,在票房上,他们拒绝接受代币,因此您决定尝试一下运气。 大厅里有很多老虎机可以玩。 对于带有老虎机的游戏,您使用一个令牌。 如果赢了,机器给您一美元,如果出现损失,您什么也没有。 每台机器都有固定的获胜概率(您不知道),但是对于不同的机器而言,获胜的概率是不同的。 在研究了这些机器制造商的网站之后,您发现在制造阶段,从带有某些参数的
beta分布中随机选择每台机器获胜的概率。
您想最大化您的预期奖金。
I / O格式和示例输入格式
一个执行可能包含多个测试。
每次测试都以这样的事实开始:该行上的程序包含两个整数,每个整数之间用空格隔开:数字N是包中令牌的数量,而M是大厅中的机器数量(N≤10
4 ,M≤min(N,100) ) 下一行包含两个实数α和β(1≤α,β≤10)-获胜概率的beta分布参数。
与检查系统的通信协议是这样的:您恰好发出了N个请求。 对于每个请求,请在单独的行中打印将要播放的机器的编号(从1到M)。 作为答案,在单独的一行中将是“ 0”或“ 1”,分别表示在使用请求的老虎机的游戏中的输赢。
在最后一次测试后,将不再是数字N和M,而是两个零。
输出格式
如果您的决定不比陪审团的决定差很多,则认为该任务已完成。 如果您的决定比陪审团的决定差很多,您将收到判决“错误答案”。
可以保证,如果您的决定不差于陪审团的决定,那么收到判决“错误答案”的可能性不会超过
10-6 。
注意事项
互动示例:
____________________ stdin stdout ____________________ ____________________ 5 2 2 2 2 1 1 0 1 1 2 1 2 1
解决方案
这个问题是众所周知的,可以用不同的方法解决。 陪审团的主要决定是实施
汤普森(Thompson)抽样策略,但由于在程序开始时就知道了步骤数,因此有更多的最佳策略(例如UCB1)。 而且,甚至可以通过epsilon-greedy-strategy来解决:以一定的概率ε玩随机机器,以(1-ε)的概率玩具有最佳胜利统计数据的机器。
class SolverFromStdIn(object): def __init__(self): self.regrets = [0.] self.total_win = [0.] self.moves = [] class ThompsonSampling(SolverFromStdIn): def __init__(self, bandits_total, init_a=1, init_b=1): """ init_a (int): initial value of a in Beta(a, b). init_b (int): initial value of b in Beta(a, b). """ SolverFromStdIn.__init__(self) self.n = bandits_total self.alpha = init_a self.beta = init_b self._as = [init_a] * self.n
C.句子对齐
条件
训练良好的机器翻译模型最重要的任务之一就是并行句子的案例。 通常,并行报价的来源是并行文档。 事实证明,通常情况下,为了建立平行句子的特定语料库,您不需要知道其长度即可。 特别是,您可能会注意到源语言中的句子越长,最有可能被翻译的时间就越长。 困难之处在于,在翻译过程中,文本中句子的数量会发生变化:有时候,翻译中的两个相邻句子可以合并为一个,反之亦然-一个句子可以分为两个。 在极少数情况下,翻译中的句子可能会被完全省略,或者翻译可能会出现在原文以外的译文中。
更正式地说,假设以下针对并行机柜的生成模型是正确的。 在每一步中,我们执行以下操作之一:
1. 停止以概率p
h结束船体
的生成。
2. [1-0] 跳过报价我们以概率
d d将一句话归于原文。 我们不将任何翻译归因于翻译。 从离散分布中选择原始语言L≥1的句子长度:
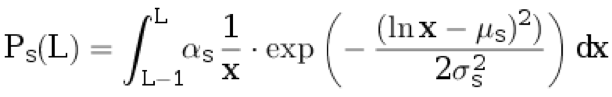
。
这里,
μs ,
σs是分布参数,而
αs是选择的归一化系数,因此

。
3. [0-1] 插入提案我们以概率p
i为翻译指定一个句子。 我们没有将任何东西归因于原件。 从不连续的分布中选择翻译语言中L≥1的句子长度:

。
其中,
μt ,
σt是分布参数,而
αt是选择的归一化系数,因此

。
4. 翻译以概率(1- p
d -p
i -p
h )从分布ps中取原始语言L s≥1的句子长度(四舍五入)。 接下来,我们根据条件离散分布生成翻译语言L t≥1的句子长度:
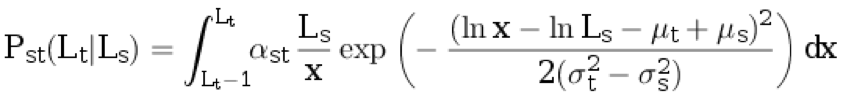
。
在此,
αst是归一化系数,其余参数在前面的段落中进行了描述。
下一步是另一个步骤:
1. [2-1]通过概率p
split s,原始语言中生成的句子被分为两个非空句子,因此单词的总数
正好增加了一个 。 长度为L
s的句子分解为长度为L
1和L
2的部分 (即L
1 + L
2 = L
s +1)的概率与P
s (L
1 )⋅P
s (L
2 )成比例。
2. [1-2]通过概率p
split t,目标语言中生成的句子分为两个非空句子,因此单词总数增加了一个。 长度为L
t的句子分解为长度为L1和L2的部分(即L
1 + L
2 = L
t +1)的概率与P
t (L
1 )⋅P
t (L
2 )成比例。
3. 3. [1-1]以(1-p
split s -p
split t )的概率,这对生成的句子都不会衰减。
I / O格式,示例和注释输入格式
文件的第一行包含分布参数:p
h ,p
d ,p
i ,p
split s ,p
split t ,
μs ,σs,μt,σt。 0.1≤σs <σt≤3. 0≤μs,μt≤5。
下一行包含数字N
s和N
t-在这种情况下分别以原始语言和目标语言显示的句子数(1≤N
s ,N t≤1000)。
下一行包含N
s个整数-原始语言中句子的长度。 下一行包含N
t个整数-目标语言中句子的长度。
下一行包含两个数字:j和k(1≤j≤N
s ,1≤k≤N
t )。
输出格式
需要推导在文本中分别具有索引j和k的句子是平行的概率(也就是说,它们是在算法的一步生成的,并且都不是衰减的结果)。
如果绝对误差不超过10
–4,您的答案将被接受。
例子1
例子2
例子3
注意事项
在第一个示例中,可以通过三种方式获得数字的初始序列:
•首先,以概率p
d在原始文本中添加一个句子,然后以概率p
i将一句话添加到翻译中,然后以概率p
h完成生成。
此事件的概率为P
1 = p
d * P
s (4)* p
i * P
t (20)* p
h 。
•首先,以概率p
d在原始文本中添加一个句子,然后以概率p
i将一句话添加到翻译中,然后以概率p
h完成生成。
此事件的概率等于P
2 = p
i * P
t (20)* p
d * P
s (4)* p
h 。
•以概率(1--p
h -p
d -p
i )生成两个句子,然后以概率(1--p
split s -p
split t )保留一切(即,不要将原文或译文分成两个句子) ),然后以p
h的概率结束生成。
此事件的概率为

。
结果,答案计算为

。
解决方案
该任务是使用隐藏马尔可夫模型进行对齐的一种特殊情况(HMM对齐)。 主要思想是,您可以使用此模型和
正向算法来计算生成一对特定文档的概率:在这种情况下,状态是一对文档前缀。 因此,可以通过
向前-向后算法来计算特定的平行句子对的对齐所需的概率。
代号 #include <iostream> #include <iomanip> #include <cmath> #include <vector> double p_h, p_d, p_i, p_tr, p_ss, p_st, mu_s, sigma_s, mu_t, sigma_t; double lognorm_cdf(double x, double mu, double sigma) { if (x < 1e-9) return 0.0; double res = std::log(x) - mu; res /= std::sqrt(2.0) * sigma; res = 0.5 * (1 + std::erf(res)); return res; } double length_probability(int l, double mu, double sigma) { return lognorm_cdf(l, mu, sigma) - lognorm_cdf(l - 1, mu, sigma); } double translation_probability(int ls, int lt) { double res = length_probability(ls, mu_s, sigma_s); double mu = mu_t - mu_s + std::log(ls); double sigma = std::sqrt(sigma_t * sigma_t - sigma_s * sigma_s); res *= length_probability(lt, mu, sigma); return res; } double split_probability(int l1, int l2, double mu, double sigma) { int l_sum = l1 + l2; double total_prob = 0.0; for (int i = 1; i < l_sum; ++i) { total_prob += length_probability(i, mu, sigma) * length_probability(l_sum - i, mu, sigma); } return length_probability(l1, mu, sigma) * length_probability(l2, mu, sigma) / total_prob; } double log_prob10(int ls) { return std::log(p_d * length_probability(ls, mu_s, sigma_s)); } double log_prob01(int lt) { return std::log(p_i * length_probability(lt, mu_t, sigma_t)); } double log_prob11(int ls, int lt) { return std::log(p_tr * (1 - p_ss - p_st) * translation_probability(ls, lt)); } double log_prob21(int ls1, int ls2, int lt) { return std::log(p_tr * p_ss * split_probability(ls1, ls2, mu_s, sigma_s) * translation_probability(ls1 + ls2 - 1, lt)); } double log_prob12(int ls, int lt1, int lt2) { return std::log(p_tr * p_st * split_probability(lt1, lt2, mu_t, sigma_t) * translation_probability(ls, lt1 + lt2 - 1)); } double logsum(double v1, double v2) { double res = std::max(v1, v2); v1 -= res; v2 -= res; v1 = std::min(v1, v2); if (v1 < -30) { return res; } return res + std::log(std::exp(v1) + 1.0); } double loginc(double* to, double from) { *to = logsum(*to, from); } constexpr double INF = 1e25; int main(void) { using std::cin; using std::cout; cin >> p_h >> p_d >> p_i >> p_ss >> p_st >> mu_s >> sigma_s >> mu_t >> sigma_t; p_tr = 1.0 - p_h - p_d - p_i; int Ns, Nt; cin >> Ns >> Nt; using std::vector; vector<int> ls(Ns), lt(Nt); for (int i = 0; i < Ns; ++i) cin >> ls[i]; for (int i = 0; i < Nt; ++i) cin >> lt[i]; vector< vector< double> > fwd(Ns + 1, vector<double>(Nt + 1, -INF)), bwd = fwd; fwd[0][0] = 0; bwd[Ns][Nt] = 0; for (int i = 0; i <= Ns; ++i) { for (int j = 0; j <= Nt; ++j) { if (i >= 1) { loginc(&fwd[i][j], fwd[i - 1][j] + log_prob10(ls[i - 1])); loginc(&bwd[Ns - i][Nt - j], bwd[Ns - i + 1][Nt - j] + log_prob10(ls[Ns - i])); } if (j >= 1) { loginc(&fwd[i][j], fwd[i][j - 1] + log_prob01(lt[j - 1])); loginc(&bwd[Ns - i][Nt - j], bwd[Ns - i][Nt - j + 1] + log_prob01(lt[Nt - j])); } if (i >= 1 && j >= 1) { loginc(&fwd[i][j], fwd[i - 1][j - 1] + log_prob11(ls[i - 1], lt[j - 1])); loginc(&bwd[Ns - i][Nt - j], bwd[Ns - i + 1][Nt - j + 1] + log_prob11(ls[Ns - i], lt[Nt - j])); } if (i >= 2 && j >= 1) { loginc(&fwd[i][j], fwd[i - 2][j - 1] + log_prob21(ls[i - 1], ls[i - 2], lt[j - 1])); loginc(&bwd[Ns - i][Nt - j], bwd[Ns - i + 2][Nt - j + 1] + log_prob21(ls[Ns - i], ls[Ns - i + 1], lt[Nt - j])); } if (i >= 1 && j >= 2) { loginc(&fwd[i][j], fwd[i - 1][j - 2] + log_prob12(ls[i - 1], lt[j - 1], lt[j - 2])); loginc(&bwd[Ns - i][Nt - j], bwd[Ns - i + 1][Nt - j + 2] + log_prob12(ls[Ns - i], lt[Nt - j], lt[Nt - j + 1])); } } } int j, k; cin >> j >> k; double rlog = fwd[j - 1][k - 1] + bwd[j][k] + log_prob11(ls[j - 1], lt[k - 1]) - bwd[0][0]; cout << std::fixed << std::setprecision(12) << std::exp(rlog) << std::endl; }
D.建议带
条件
考虑有关异构内容的建议的提要。 它混合了各种类型的对象(图片,视频,新闻等)。 这些对象通常是根据与用户的相关性来排序的:与用户相关性(兴趣)越高的对象,则越接近推荐列表的顶部。 但是,通过这种排序,经常会出现以下情况:相同类型的多个对象出现在建议列表中。 这极大地恶化了我们建议的外部种类,因此用户不喜欢它。 根据建议列表,有必要实现一种算法,该算法将组成一个新列表,该列表将摆脱此问题并且最相关。
假设初始建议列表为a = [a
0 ,a
1 ,...,a
n-1 ],且长度n>0。编号为i的对象的类型编号为b i∈{0,...,m-1}。 此外,编号为i的对象的相关性为r(
ai )= 2
-i 。 考虑通过选择对象的子集并重新排列对象而从初始对象中获得的列表:x = [a
i 0 ,
ai 1 ,...,
ai k − 1 ],长度为k(0≤k≤n)。 如果列表中没有两个连续的对象在类型上重合,即所有i = 0,...,k − 2的b
i j ≠b
i j + 1 ,则称该列表为可允许的。 列表的相关性由公式计算
。 您需要找到所有有效的最大关联列表。
I / O格式和示例输入格式
在第一行,数字n和m以空格(1≤n≤100000,1≤m≤n)书写。 接下来的n行包含数字
i ,其中i = 0,...,n-1(0≤b i≤m-1)。
输出格式
用空格写下最终列表中的对象数:i
0 ,i
1 ,...,i
k − 1 。
例子1
例子2
例子3
解决方案
使用简单的数学计算,可以证明,可以通过“贪心”方法解决问题,即,在最佳建议列表中,每个项目的最相关对象在列表的同一开头都是有效的。 这种方法的实现很简单:如果可能,我们将对象连续放入并添加到答案中。 当遇到无效的对象(其类型与上一个对象的类型一致)时,我们将其放在单独的队列中,然后将其从队列中尽快插入到响应中。 请注意,在每个时刻,此队列中的所有对象都将具有匹配的类型。 最后,几个对象可能会保留在队列中,它们将不包含在响应中。
std::vector<int> blend(int n, int m, const std::vector<int>& types) { std::vector<int> result; std::queue<int> repeated; for (int i = 0; i < n; ++i) { if (result.empty() || types[result.back()] != types[i]) { result.push_back(i); if (!repeated.empty() && types[repeated.front()] != types[result.back()]) { result.push_back(repeated.front()); repeated.pop(); } } else { repeated.push(i); } } return result; }
D.字符序列的聚类
有一个有限的字母A = {a
1 ,a
2 ,...,a
K-1 ,a
K = S},a i∈{a,b,...,z},S是行的结尾。
考虑以下在字母A上生成随机字符串的方法:
1.第一个字符x
1是一个随机变量,其分布为P(x
1 = a
i )= q
i (已知q
K = 0)。
2.根据条件分布P(x
i = a
j || x
i-1 = a
l )= p
jl ,根据前一个字符生成每个下一个字符。
3.如果x
i = S,则生成停止,结果为x
1 x
2 ... x
i − 1 。
给出了由两个描述的具有不同参数的模型的混合生成的线组。 每行都必须给出生成它的链的索引。
I / O格式,示例和注释输入格式
第一行包含两个数字1000≤N≤2000和3≤K≤27-分别是行数和字母的大小。
第二行包含由K-1个不同的拉丁字母小写字母组成的行,指示字母表中的前K-1个元素。
随后的N条线中的每条线均根据条件中描述的算法生成。
输出格式
在第N行中,第i行包含输入文件的第i + 1行上序列的簇号(0/1)。 与真实答案的重合度应至少为80%。
例子
注意事项
请从以下条件开始测试:在其中,前50行是从分布生成的
P(x
i = a | x
i-1 = a)= 0.5,P(x
i = S | x
i-1 = a)= 0.5,P(x
1 = a)= 1; 第二50-从发行
P(x
i = b | x
i-1 = b)= 0.5,P(x
i = S | x
i-1 = b)= 0.5,P(x
1 = b)= 1。
解决方案
使用
EM算法解决了该问题:假设所提供的样本是由两个马尔可夫链的混合生成的,其参数在迭代过程中得以恢复。 限制了80%的正确答案,以使解决方案的正确性不受两个链中都具有高概率的示例的影响。 因此,这些示例在正确还原后可以分配给在生成的响应方面不正确的链。
import random import math EPS = 1e-9 def empty_row(size): return [0] * size def empty_matrix(rows, cols): return [empty_row(cols) for _ in range(rows)] def normalized_row(row): row_sum = sum(row) + EPS return [x / row_sum for x in row] def normalized_matrix(mtx): return [normalized_row(r) for r in mtx] def restore_params(alphabet, string_samples): n_tokens = len(alphabet) n_samples = len(string_samples) samples = [tuple([alphabet.index(token) for token in s] + [n_tokens - 1, n_tokens - 1]) for s in string_samples] probs = [random.random() for _ in range(n_samples)] for _ in range(200): old_probs = [x for x in probs]
.