手动肺分割大约需要10分钟,并且需要一定的技能才能获得与自动分割相同的高质量结果。 自动分段大约需要15秒。
我以为没有神经网络,准确度就不会超过70%。 我还假设形态学操作只是为更复杂的算法准备图像。 但是,由于处理了这些手部断层扫描数据,尽管数量很少,但只有40个,该算法对肺部进行了分割,没有错误。 此外,在前五种情况下进行测试后,该算法并未发生明显变化,并且在不更改设置的情况下,在其他35项研究中也能正常工作。
同样,神经网络也有一个缺点-对于其训练,我们需要数百个肺部训练样本,这些样本需要手动标记。
内容内容
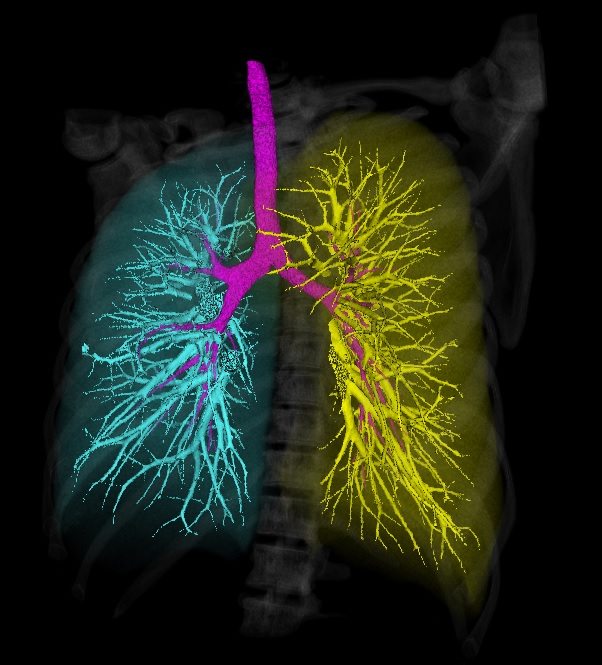
呼吸系统的结构
呼吸系统包括气道和肺。 气道分为上,下气道。 下呼吸道和上呼吸道之间的分离点是食道与气道的交点。 喉部上方的所有器官均为上呼吸道,喉部下方的所有器官均为下呼吸道。
呼吸器官清单:
鼻腔是在鼻子和咽之间的充满空气的腔。
咽是食物和空气传播的通道。
气管是连接到喉和支气管的管。
喉负责声音的形成。 它位于颈椎C4-C6的水平。
支气管是呼吸道,其主要部分位于肺部内部。
肺是主要的呼吸器官。

豪恩斯菲尔德量表
戈弗雷·霍恩斯菲尔德(Godfrey Hounsfield)是一位英国电气工程师,他与美国理论家艾伦·科马克(Allan Cormack)一起开发了计算机断层扫描技术,为此他在1979年获得了诺贝尔奖。

霍恩斯菲尔德标度-是描述无线电密度的定量标度,以霍恩斯菲尔德为单位测量,表示为HU。
辐射密度是根据辐射衰减系数计算的。 衰减系数表征了一定数量的材料可以被辐射穿透的程度。
辐射密度通过以下公式计算:
$$显示$$ {μ_{X}-μ_{water} \超过μ_{water}-μ_{air}} \乘以1000 $$ display $$
在哪里 是被测材料,水和空气的线性衰减系数。
放射性密度可以为负,因为零放射性密度对应于水。 这意味着所有具有比水衰减系数低的衰减系数的材料(例如,肺组织,空气)将具有负的放射性密度。
下面列出了各种组织的大约射线密度:
- 空气:-1000 HU。
- 呼吸器官:-950至-300 HU。
- 血液(不与血管形成对比):从0到100 HU。
- 骨骼:100至1000 HU。

链接到Wikipedia: 霍恩斯菲尔德标度 , 戈弗雷·霍恩斯菲尔德 , 衰减系数 。
数学形态
形态学运算是算法中使用的主要工具。
在计算机视觉领域,形态学运算被称为一组用于变换对象形状的算法。 最常见的是,形态学运算应用于二进制化的图像,其中单位对应于对象体素,零对应于空白。
主要的形态学操作包括:
形态膨胀是向对象的所有边缘体素添加新的体素。 换句话说,算法扫描与对象边缘相对应的所有体素,并使用具有给定形式(球形,立方体,十字形等)的内核将其放大。 核具有自己的半径(对于球体)或侧面的宽度(对于立方体)。 此操作通常用于将多个附近的对象合并为一个对象。
形态侵蚀是位于对象边界(边界)上的所有体素的截止。 此操作与扩张相反。 此操作对于消除许多小的互连对象形式的噪声很有用。 但是,仅当目标物体的厚度比腐蚀半径大得多时,才应使用这种噪声消除方法。 否则,有用的信息将丢失。
形态学上的闭合是扩张,随后是侵蚀。 它用于封闭对象内部的孔并合并附近的对象。
形态开放是侵蚀然后扩张。 它用于去除小噪音对象并将这些对象分成几个对象。

Lee算法和RLE压缩
为了选择二值化体素体积中的对象,使用了Lie算法。 最初,发明该算法是为了找到走出迷宫的最短路径。 我们使用它来选择对象,并将其从三维三维像素阵列移动到另一个三维像素阵列。 该算法的基本思想是从起点开始在所有可能的方向上平行移动。 对于三维情况,可以从一个体素沿26或6个方向移动。
为了优化性能,应用了行程编码算法。 该算法的主要思想是将一和零的序列替换为一个数字,该数字等于该序列中元素的数量。 例如,字符串“ 00110111”可以替换为:“ 2; 2; 1; 3“。 这减少了内存访问的次数。
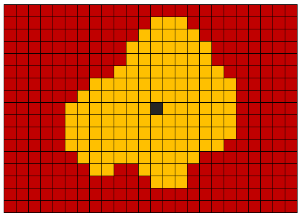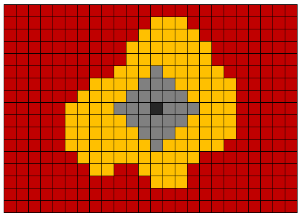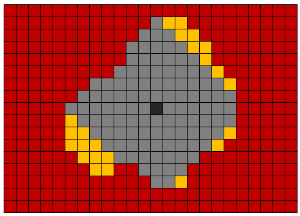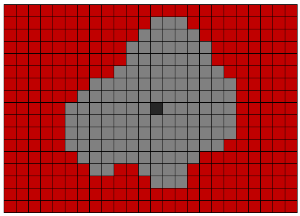

Wikipedia链接: Lee算法 , RLE算法 。
基本体积的阈值转换
使用断层扫描仪,获得了在扫描空间每个点的射线密度数据。 空气体素的辐射密度为-1100至-900 HU,呼吸器官体素的辐射密度为-900至-300 HU。 因此,我们可以删除所有辐射密度大于-300 HU的不必要体素。 结果,我们获得了仅包含呼吸器官和空气的二值化体素体积。
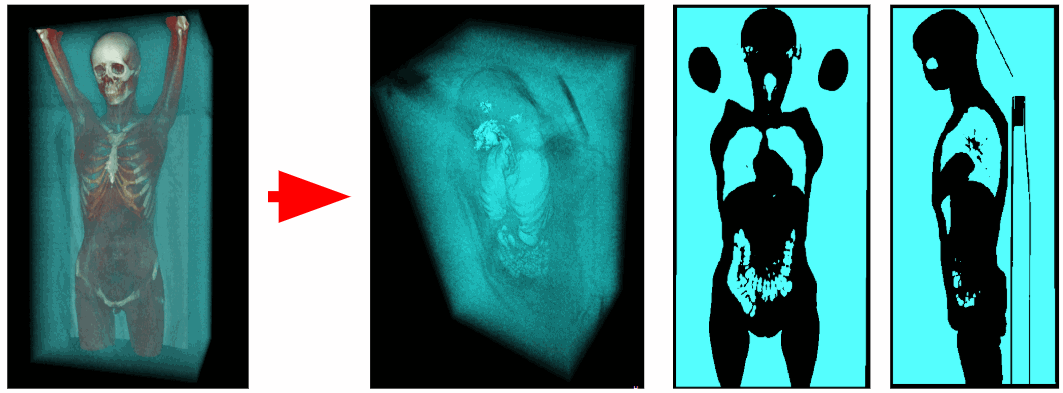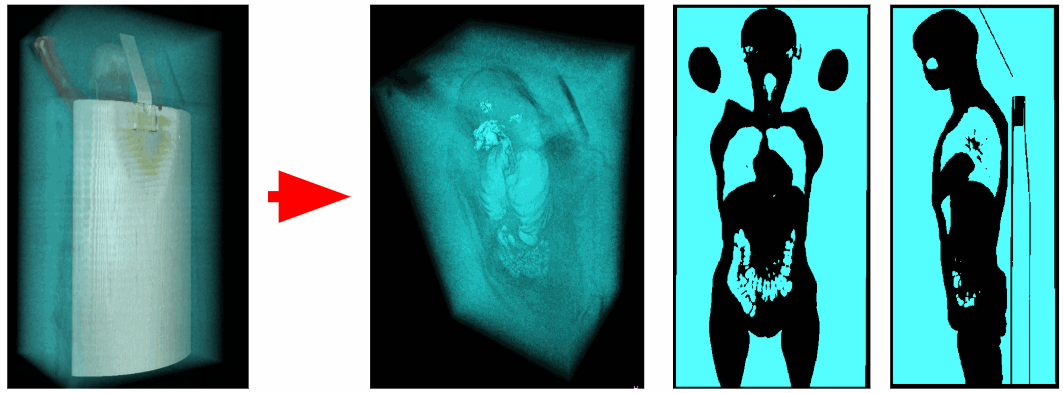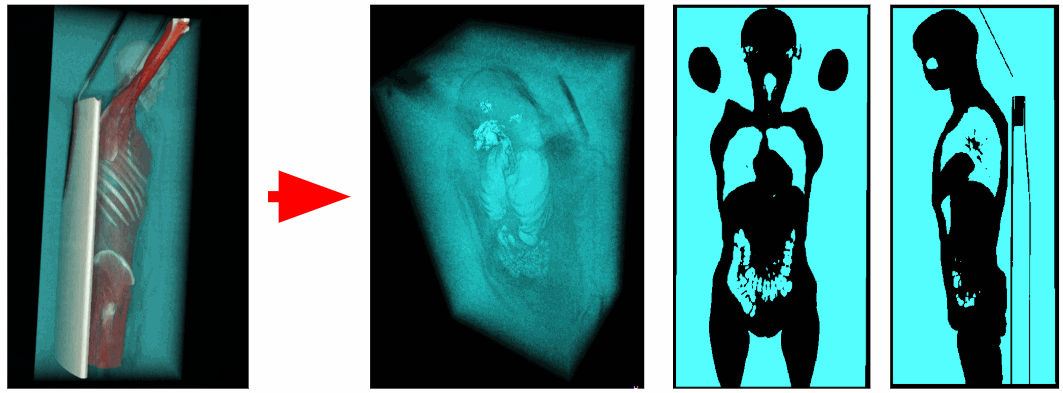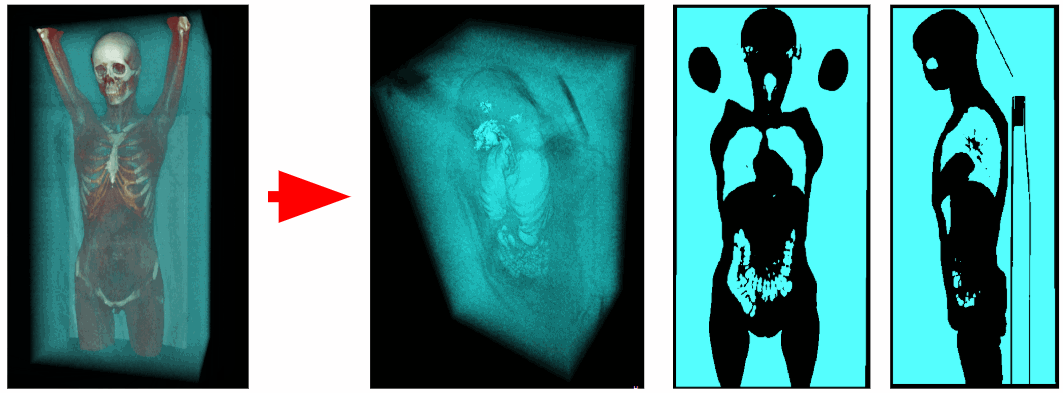
外部空气排出
为了分割身体的内部空气,我们删除了3D立体角附近的所有对象。 因此,我们去除了外部空气。

但是,并非所有情况都可以消除断层扫描仪工作台中的空气,因为断层扫描仪工作台可能与3D体积的角部没有任何联系。

因此,我们不仅将扫描角,而且将扫描位于f的任何边缘平面上的所有体素。 但是,如下图所示,肺也被切除了。 事实证明,气管还与3D体积的上平面有关。
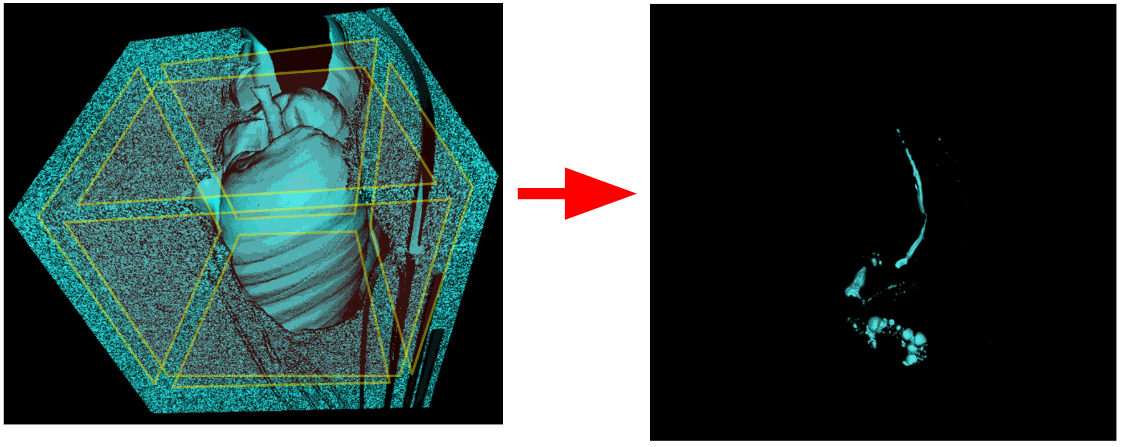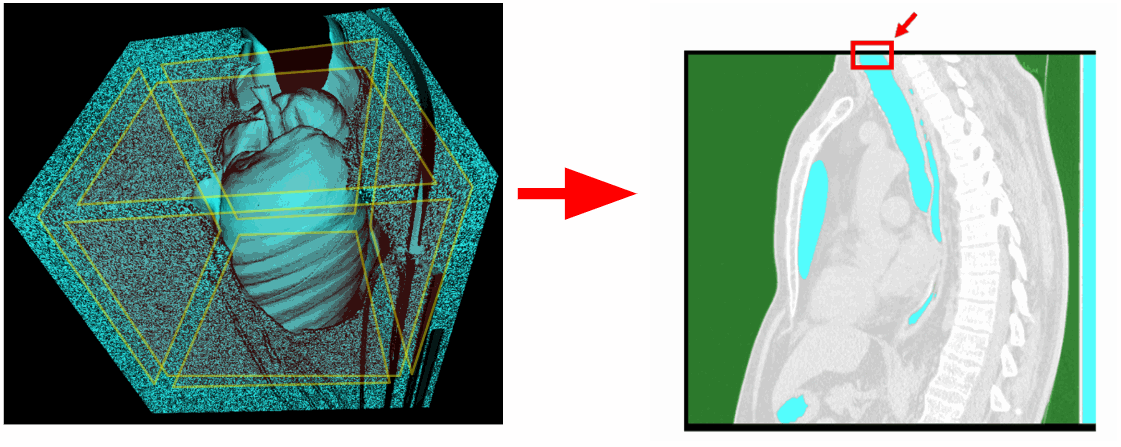
我们必须从扫描区域中排除顶部平面。 也有研究未完全捕获肺部,并且下平面与肺部相连。
因此,如果您愿意,也可以排除下平面。

但是这种方法仅影响胸部研究。 在捕获全部身体的情况下,将出现通过鼻腔的内部和外部空气的连接。因此,有必要进行形态学侵蚀以分离内部和外部空气。
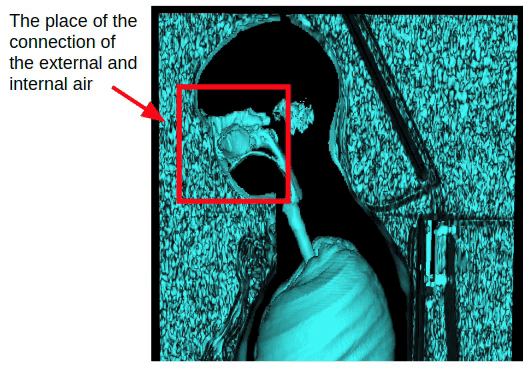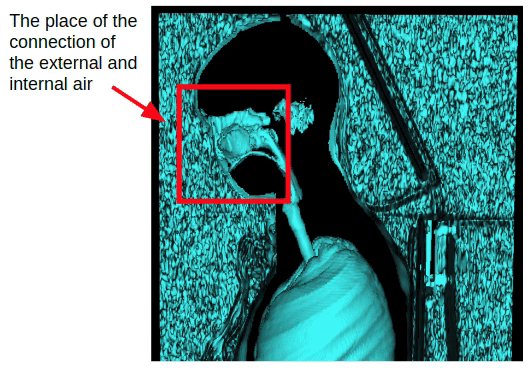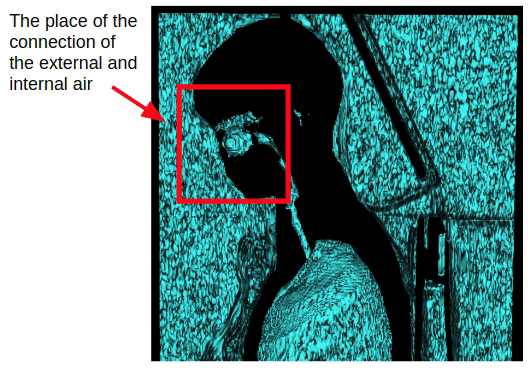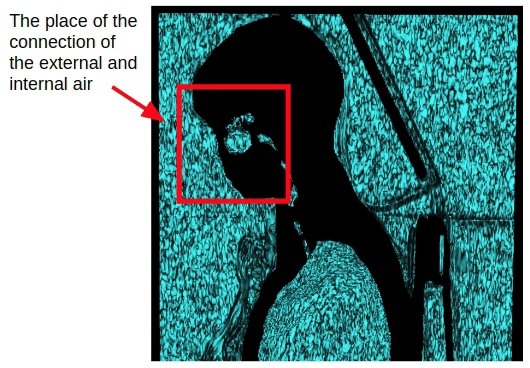
施加腐蚀之后,我们可以返回之前获得的外部空气分割方法,该方法基于外部空气与3D体积侧面的连通性。

在对外部空气进行分割之后,我们可以立即从空气和肺的全部体积中减去外部空气,从而获得身体和肺部的内部空气。 但是有一个问题。 侵蚀后,有关外部空气的一些信息丢失了。 为了恢复它,我们应用外部空气膨胀。

接下来,我们从整个空气和呼吸器官中减去外部空气,得到内部空气和呼吸器官。


最大体积对象的分割
接下来,我们将呼吸器官分割为体积最大的对象。 呼吸器官与胃肠道内的空气无关。


值得注意的是,在初始步骤正确选择射线密度阈值很重要。 否则,在某些情况下,由于分辨率低,两个肺之间可能没有连接。 例如,如果我们假设呼吸器官的体素具有-500 HU及以下的放射密度,则在以下情况下,将呼吸器官分割为体积最大的对象将导致错误,因为两个肺。 因此,阈值应增加到-300 HU。

关闭肺部血管
为了捕获肺内的血管,我们将使用形态学上的闭合,即扩张,然后以相同的半径进行侵蚀。 血管的放射密度(无反差)约为0..100 HU。

在图像中,我们可以看到没有关闭大的血液通道。 但这不是必需的。 此操作的目的是破坏肺内的许多小孔,以简化后续步骤中的肺分割过程。
呼吸器官分割算法
结果,我们获得了以下呼吸器官分割算法:
- 具有阈值“ <-300 HU”的基本卷的阈值变换。
- 半径为3 mm的形态腐蚀,用于外部和内部空气的分离。
- 基于外部空气与3D体积边界侧平面的连通性对外部空气进行细分。
- 外部空气的形态膨胀可恢复侵蚀后丢失的信息。
- 从整个空气和呼吸器官中减去外部空气以获得内部空气和呼吸器官。
- 最大体积对象的分段。
- 肺内血管的形态闭合。

MATLAB中的算法实现
函数“ getRespiratoryOrgans”
函数“ getExternalAir”
函数“ getMaxObject”
可以通过参考下载源代码。
结论
以下文章将是:
- 气管和支气管分割;
- 肺分割
- 肺叶分割。
将考虑以下算法:
- 距离变换
- 最近邻变换,也称为特征变换;
- 计算用于分割平面3D对象的Hessian矩阵的特征值;
- 分水岭分割。